土体强度对T-bar系数修正影响的研究
2022-12-19魏子钧王宝忠
魏子钧,王宝忠
(中水东北勘测设计研究有限责任公司,吉林 长春 130021)
0 引言
软土强度测试是室内土工试验和现场原位测试的重要组成部分,因具有可以测量土体强度沿深度包络线的优势,贯入试验自提出以来即获得室内试验的大量应用。其中,最早由Stewart 和Randolph 在1994年提出的T-bar 贯入仪应用最为广泛[1]。T-bar 贯入端头为圆柱体,基于测量得到贯入端头阻力qc,土体的不排水抗剪强度Su计算公式:

式中:N为T-bar系数。由此可见,T-bar贯入仪测量软土强度结果的准确性依赖于强度系数的选取。
当T-bar 在软土中贯入一定深度后,土体会绕着贯入端头达到全流动状态,此时T-bar 系数可以取为10.5[2]。由于T-bar 贯入仪操作简便、测试结果精确可靠,已经被广泛应用于软黏土的不排水抗剪强度测试中[3,4]。但是,当T-bar 贯入土中深度不足以形成全回流机制时,T-bar 系数介于5.4~10.5,此时需要对T-bar 系数进行修正才能准确地获得土体的不排水抗剪强度[5]。
本文应用Abaqus 软件,基于CEL 方法计算了T-bar 贯入不同抗剪强度土体过程中不同深度处对应系数的取值,并探讨了土体抗剪强度对T-bar系数的影响。
1 计算模型
耦合的欧拉-拉格朗日有限元分析法(Coupled Eulerian-Lagrangian,简称为CEL 方法)基于中心差分的动态显示求解,对变形较大的土体采用欧拉网格剖分,而对刚度较大的结构物则采用拉格朗日网格剖分,综合了欧拉分析和拉格朗日分析的优点,已经被证明可以有效地模拟结构物在土中的贯入问题[6-9]。
CEL计算设置与文献[9]相同:T-bar和土体均采用八节点方块单元;在土体表面上方设置厚度为2D(D为T-bar 直径)的空欧拉单元以适应T-bar贯入过程中土体表面的隆起;T-bar 直径为5 mm,长度为20 mm,土体的厚度为20 mm;土体模型为均质粘土,取浮重度650 kN/m3,采用摩尔库伦屈服准则,不排水抗剪强度为1.0 kPa,弹性模量为300Su(Su为土体不排水抗剪强度),泊松比为0.49;T-bar模型为刚体,与土之间为通用接触。
2 计算结果
计算结果中,作用在T-bar 模型表面上沿Z方向的作用力为Fz,即为作用在T-bar 贯入端头上土体的作用力,则T-bar 上的端阻力qc可以通过下式计算:

式中:A为力的作用面积在Z方向上的投影。
随着T-bar端头的贯入深度不同需要分段计算:

式中:Z为T-bar贯入土体深度;L为T-bar的长度。
结合式(1),可以得到T-bar系数的计算表达式:

为了讨论土体不排水抗剪强度Su对T-bar 修正系数N的影响,计算了Su为0.5,1.0,2.0 及5.0 kPa 总计4 种工况,计算结果均绘制于图1中。4 种Su条件下计算得到的T-bar 系数随贯入深度变化曲线的形状基本没有变化,满足如下的变化规律:随着贯入深度的增加,T-bar 系数首先减小,然后逐渐增加至9.8~10.0[9]。但是,随着Su的增加,曲线整体向右上方有小幅移动。
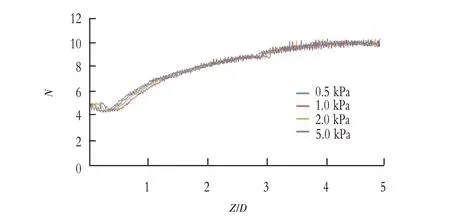
图1 不同强度土体T-bar 系数曲线
3 修正的T-bar 系数
文献[9]提出可以简单方便地计算T-bar 修正系数N*随深度变化的表达式:

式中:a和b为T-bar 修正系数计算表达式的待定系数,由数据拟合得到。
由于土体不排水抗剪强度Su对T-bar系数随深度变化规律几乎没有影响,即仍然可以用式(6)来进行描述。根据文中不同Su条件下的计算结果对式(6)中的系数a和b进行拟合,结果列入表1中。
由表1可以看出,在计算工况Su=0.5~5.0 kPa条件下,系数a和b分别随着Su的增加而增大和减小,且为非线性变化规律,为了可以更好地描述a和b随Su的变化规律,将a和b随Su变化数据及拟合结果绘制于图2中。

表1 不同Su 条件下式(6)系数列表

图2 系数a 和b 拟合结果
对系数a和b采用幂函数来进行拟合,得到的表达式:

式(7)和(8)对系数a和b计算数据的拟合精度分别达到了R2=0.965 和R2=0.985,可以非常好地描述系数a和b随着Su的变化关系。
综上,将修正T-bar 数据的流程总结如下:第一步,预估土体不排水抗剪强度Su0,通过式(7)和(8)计算得到对应的系数a和b。第二步,通过式(6)计算得到T-bar 修正系数N*。第三步,根据T-bar 实测数据计算得到土体的不排水抗剪强度Su1。第四步,比较Su1和Su0的差值△,若差值△较小,则Su1即为真实的土体不排水抗剪强度;若差值△较大,则将Su0替换为此时计算得到的Su1,重复第一至第四步,直到Su1和Su0的差值满足精度要求。
4 结语
上述研究应用CEL 大变形有限元方法,计算模拟了T-bar 在不排水抗剪强度为0.5~5.0 kPa 软土中的贯入过程,重点关注不同土强度中T-bar系数的修正方法,得到如下结论。
1)T-bar 修正公式中,待定系数a随着土体不排水强度的增加而减小,待定系数b随着土体不排水强度的增加而增大,且均为非线性变化关系,可以通过幂函数来描述该变化规律。在计算工况所模拟的土体强度范围内,本文对系数a和b拟合结果的精度很高。
2)给出了修正T-bar 数据的流程。该方法初始假定土体强度,通过计算得到的系数a和b来计算修正的T-bar 系数,进而计算得到土体强度,然后经过迭代获得真实的土体不排水抗剪强度。
需要指出的是,本文提出的T-bar 系数的修正方法是基于土体强度为0.5~5.0 kPa 的大变形有限元计算结果提出的,如果应用条件超出该范围,还需要补充相应的大变形数值计算或者模型试验数据进行校验和修正。
