基于五阶Bezier曲线的无人车避障轨迹规划

陈鹏宇, 孔令安,2,3， 彭忆强,2,3*

(1.西华大学汽车与交通学院， 成都 610039； 2.汽车测控与安全四川省重点实验室， 成都 610039； 3.四川省新能源汽车智能控制与仿真测试技术工程研究中心， 成都 610039)

据公安部统计，截至2021年底全国机动车保有量达3.95亿辆，其中汽车3.02亿辆；2021年全国新注册登记机动车3 674万辆，比2020年增加346万辆，增长10.38%[1]。在为出行增加便利的同时，随之带来的交通拥堵和安全问题开始变得日益突出。面对机动车不断快速增长带来的问题，各界普遍认为发展以计算机控制代替人工驾驶的自动驾驶汽车会是有效解决手段之一[2]。

无人驾驶作为主要的技术包括环境感知、路径规划、跟踪控制3个方面，其中路径规划作为中间环节，在无人驾驶系统中有着极为重要的作用[3]。根据规划的范围来划分，路径规划又可以分为全局路径规划和局部路径规划。全局路径规划是在整个地图上规划出一条从起点到终点的可行驶的静态路径，局部路径规划是在全局路径规划的基础上根据当前实际行驶的环境规划出来的一条随环境变化无碰撞且满足各种约束的实时路径。

经过多年的技术累计，无人车的局部路径规划技术也有了很大的突破。综合来看，无人车局部路径规划技术主要可以分为以下4大类：基于图搜索的局部路径规划方法主要有 A*算法、混合 A*算法、D*算法及一系列衍生算法等[4-5]；基于随机搜索算法的局部路径规划方法主要就是快速随机搜索树(rapidly-exploring random tree， RRT)，基于曲线插值的局部路径规划方法，常用的插值曲线有直线、圆弧、多项式曲线、Bezier曲线、B样条曲线等[6]，以及基于数值优化方法的局部路径规划方法，人工势场法、最优控制等方法都是基于数值优化进行局部路径规划常采用的一些方法[7]。

由公式may=kv2(m、v、ay分别为车辆的质量、速度、横向加速度，k为道路曲率)可知,车辆通过的路径曲率应该是连续的，车辆的运动轨迹应满足侧向加速度可导，因此需要规划出来的轨迹曲线曲率可导，由此可以知道路径函数最低三阶可导。Latip等[8]研究了三阶Bezier曲线，但其规划的轨迹在起始点及终止点的道路曲率以及起始侧向加速度均不能为零，不能使车辆在实际行驶中很好地跟随轨迹； Xu等[9]基于四阶Bezier曲线提出了一种移动机器人避障路径方法，该方法规划出的路径平滑利于移动机器人跟踪，但相同情况下其轨迹曲率最大值较大；Bae等[10]对各阶Bezier曲线做了对比研究，得出满足起始点和终止点曲率均为零的最小阶Bezier曲线为五阶。为了使所规划轨迹曲线在起始点位置和终止点位置曲率均为零，采用五阶Bzeier曲线进行局部路径规划。

将五阶Bezier曲线应用于无人车局部路径规划中的问题。由于现有方法生成的轨迹曲线不能满足起始位置及终止位置曲率为零的情况，因此，车辆在跟踪开始及结束时会产生较大的侧向加速度，影响车辆轨迹跟踪的平顺性。为此，将基于五阶Bezier曲线方法加入“车辆性能边界条件”及“前车碰撞边界条件”约束，使生成的轨迹曲线在起始位置和终止位置曲率值为零，让车辆能够平稳跟踪轨迹行驶，且针对不同换道初始行驶速度，能够实现动态调整换道轨迹。

1 无人驾驶汽车避障策略

当无人车在按照预先规划好的全局路径道路上行驶时，必然会有各种各样的障碍物出现在前方道路中，为了使无人车在公路上顺利行驶，需要针对不同类型的障碍物建立不同的避障策略，典型的避障策略包括停车避障、换道避障以及跟车避障[11]。

首先，车辆将会对前方障碍物进行是否静止的判断，当前方障碍物处于静止状态时，将会优先选择换道避障，在没有可行驶道路时将会采取停车避障；当前方障碍物为动态车辆时，将会判断前车速度是否高于本车车速，优先选择跟车避障，否则选择换道或停车避障。无人车在公路上行驶时的避障策略如图1所示。

图1 无人驾驶汽车避障策略Fig.1 Obstacle avoidance strategies for driverless vehicles

2 车辆运动学建模

动力学主要研究作用于物体的力与物体运动的关系，而车辆运动学模型一般用于分析车辆的平顺性和车辆操纵的稳定性。车辆运动学转向模型如图2所示。

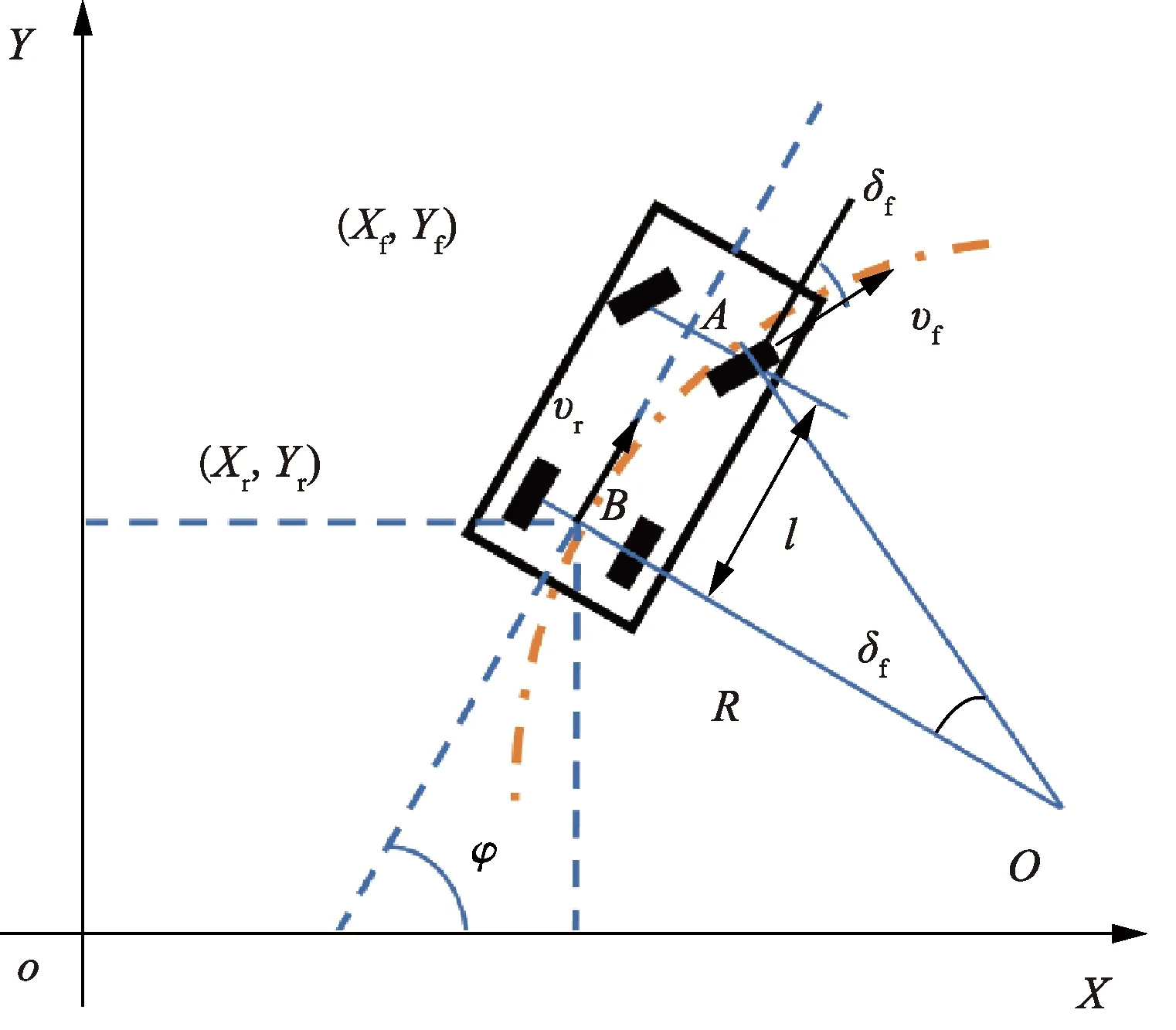
A点表示车辆前轴轴心位置；B点表示后轴轴心位置；(Xf,Yf)、(Xf,Yf)分别表示车辆前轴轴心和后轴轴心的坐标；φ为车辆航向角； vf为车辆前轴中心速度, vr为车辆后轴中心速度;δf为前轮转角；车辆转向时，瞬时转动中心为O点所在位置；R为后轮转向半径图2 车辆运动学模型[12]Fig.2 Vehicle kinematics mode[12]

道路曲率k、转向半径r、车辆轴距l以及前轮转角δf之间的关系为

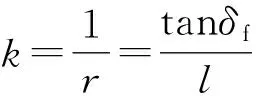
(1)

在后轮行驶轴心(Xr，Yr)处，速度为

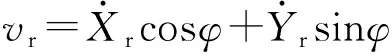
(2)

在后轴轴心B处的运动学约束为

(3)

联立式(2)和式(3)，得

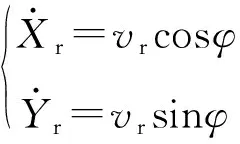
(4)

根据前、后轮的几何关系得

(5)

则由式(2)～式(4)可得横摆角速度

(6)

前轮转角为

(7)

联立式(4)和式(6)，可得车辆运动模型为

(8)

通过运动学模型就能将无人车在任意t时刻下的状态通过笛卡尔坐标(x,y)、航向角φ和道路曲率k这4个变量表示。通过这4个变量表达，则轨迹可以看作是由初始状态到终止状态的一组变量变化，设初始状态X0=[x0y0φ0k0]和终止状态XT=[xTyTφTkT][13]。

3 基于Bezier曲线的局部路径规划

3.1 五阶Bezier曲线公式

Bezier曲线对应于二维平面的数学曲线，因其控制简单，能处理光滑曲线，开始应用于无人车的局部路径规划中，通过设定曲线的起始点，并在始末点之间添加不同数量的控制点，通过改变控制点的位置坐标进而达到控制曲线弯曲方向以及弯曲角度的目的[14]。

Bezier曲线通过使用多个线段的端点坐标P0、P1、…、Pn来定义其曲线，由给定点P0、P1、…、Pn的n阶Bezier曲线可表示为通式[15]

(9)

由Bzier通式可得五次Bezier曲线公式为

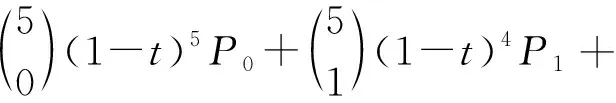
(10)

(11)

将式(11)代入式(10)可得

P(t)=(1-t)5P0+5t(1-t)4P1+

10t2(1-t)3P2+10t3(1-t)2P3+

5t4(1-t)P4+t5P5

(12)

在笛卡尔坐标系中，将车辆位置(x,y)表示成参数t的函数，则五阶Bezier曲线可以表示为

(13)

则曲线上任意一点的曲率[10]为

(14)

式(14)中：x′(t)为纵向车速；y′(t)为横向车速；x″(t)为纵向加速度；y″(t)为横向加速度。五阶Bezier曲线轨迹示意图如图3所示。

图3 五阶Bezier曲线规划轨迹示意图Fig.3 Fifth order Bezier curve planning trajectory diagram

3.2 换道避障轨迹边界条件

根据Bezier曲线的性质，需确定控制点的位置。因此，设计一种典型的需要超车换道的工况如图4所示。在封闭双车道道路内，前方车辆(或障碍物)C0静止停靠在道路右侧位置，后方车辆(本车)C1以恒定车速v1行驶，当车辆传感器检测到前方车辆静止且影响到本车行驶时，按照前文提到的避障策略，本车域控制器将从当前位置进行局部路径规划开始换道避障策略来躲避前车(或障碍物)，通过考虑车辆性能约束及前车碰撞约束来确定Bezier曲线的左右边界。

图4 典型超车换道工况Fig.4 Typical overtaking lane change condition

3.2.1 考虑车辆性能的边界

在车辆换道转向过程中，需要考虑车辆性能极限，保证车辆在转向侧翻的指标是侧向加速度的大小，如果当车辆开始变道时就以最大侧向加速度aymax=0.28gm/s2进行转向(g为重力加速度)[16]，考虑车辆性能约束的左边界圆弧半径R1计算公式为

(15)

如图5所示为性能边界所示。

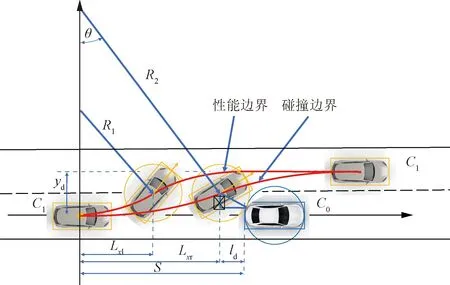
Lxl表示车辆变道开始位置到左边界位置的距离图5 轨迹规划可行域边界Fig.5 Feasible region boundary of trajectory planning

3.2.2 考虑前车碰撞的边界

当前方车辆(或障碍物)静止停靠在路边时，需考虑本车与障碍物碰撞的问题，将车辆假设为包裹车身的几何圆，则换道过程中本车与障碍物的几何圆的相切点就是不产生碰撞的约束点[17]。在本车与障碍物不发生碰撞的极限条件下开始转向，就可得到考虑碰撞问题的右边界。如图5中碰撞边界所示。

考虑碰撞问题的右边界圆弧半径R2的计算公式如下。

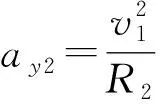
(16)

(17)

(18)

(19)

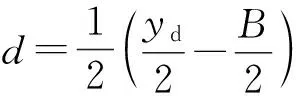
(20)

式中:ay2为侧向加速度；Lxr表示车辆变道开始位置到右边界位置的距离；yd为两条道路中心线之间的距离，取3.75 m；d为两个几何圆圆心之间的纵向距离；r为车辆几何圆半径；B为车宽；L为车长；ld为考虑碰撞问题时本车几何圆中心到障碍车后方的直线距离。在此边界条件下可得到安全换道车距S=Lxr+ld。

通过分析得到的考虑车辆性能约束的左边界圆弧半径R1和考虑前方静止障碍物避撞的右边界圆弧半径R2，就可得到换道轨迹的左右可行域边界。通过两个边界条件的约束就可得到换道轨迹的可行域范围，如图5中红色实线所围成的区域所示。

3.3 换道最优轨迹曲线选择

道路轨迹曲线规划采用五阶Bezier曲线，将选取6个不同的控制点，道路轨迹曲线则根据所选的6个控制点的改变而改变。在本研究中，以坐标原点为起始点，即P0=(x0,y0)=(0,0)；根据换道对称性，有P1=(x1,y1)=(x1,0)；P2=(x2,y2)=(x2,0)；P3=(x3,y3)=(x,yd)；P4=(x4,y4)=(2x2-x1,yd)；P5=(x5,y5)=(2x2,yd)。其中yd为两条道路中心线之间的距离，取3.75 m。因此，决定道路轨迹曲线形状的变量为选取的第二个和第三个点的纵坐标值x1和x2。

初步的左右边界判定仅仅只满足了获得车辆不侧翻以及不碰撞前车的极限情况，如果要生成的轨迹更利于车辆的跟踪行驶，那么将会加入更多的约束。为了获得最安全舒适的路径，建立了目标优化函数[18]为

J=min(ω1J1+ω2J2+ω3J3+ω4J4)

(21)

式(21)中：ω1、ω2、ω3和ω4为权重系数。

所以，目标函数公式(21)可以转化为

(22)

各优化指标的约束条件为

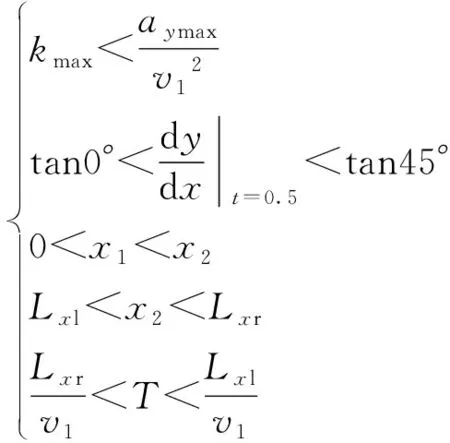
(23)

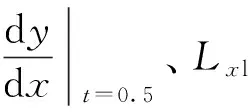
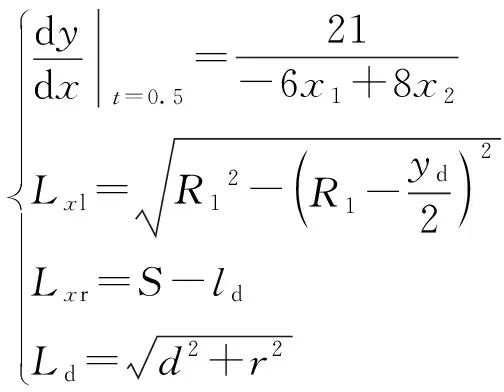
(24)

通过分析求解建立的目标函数，便可以得到不同车速下对应的最佳x1和x2，即得到6个最优坐标点信息，规划出最优行驶轨迹曲线。

3.4 换道最优轨迹曲线求解

序列二次规划(sequential quadratic programming，SQP)算法是处理规模不大非线性规划问题的最实用算法之一，此算法能够将之前推导得到的等式约束及不等式约束转换为较为简单的二次规划问题来求解[21]。整理第3.3节中所推导得到的式(23)和式(24)可得到优化目标函数为

(25)

通过SQP方法对式(25)进行最优化求解来优化控制点的选取，使最终的行驶轨迹收敛到局部最优解，得到的轨迹可使轨迹曲线更加平滑，跟踪过程满足驾乘人员乘坐舒适和车辆换道迅速的特点。

4 仿真分析

由前面分析可知，轨迹曲线形状和终止点位置由第二个和第三个控制点的纵坐标值x1和x2来决定。为分析选取不同x1和x2的值对轨迹曲线的影响进行MATLAB仿真，生成不同x1点产生的轨迹簇(取换道纵向距离为100 m，x1取值范围为16～40 m，间隔距离为6 m，x1为换道距离的中点)，得到图6所示的轨迹曲线和图7所示的轨迹曲线曲率；不同x2点产生的轨迹簇(x2取值范围为38～70 m，间隔距离为8 m，x1点为x2的中点)，得到图8所示的轨迹曲线和图9所示的轨迹曲线曲率。

图6 不同x1点产生的轨迹曲线簇Fig.6 Cluster of trajectory curves generated by different x1 points

图7 不同x1点产生的轨迹曲线曲率Fig.7 Curvature of the trajectory curve generated by different x1 points

图8 不同x2点产生的轨迹曲线簇Fig.8 Cluster of trajectory curves generated by different x2 points

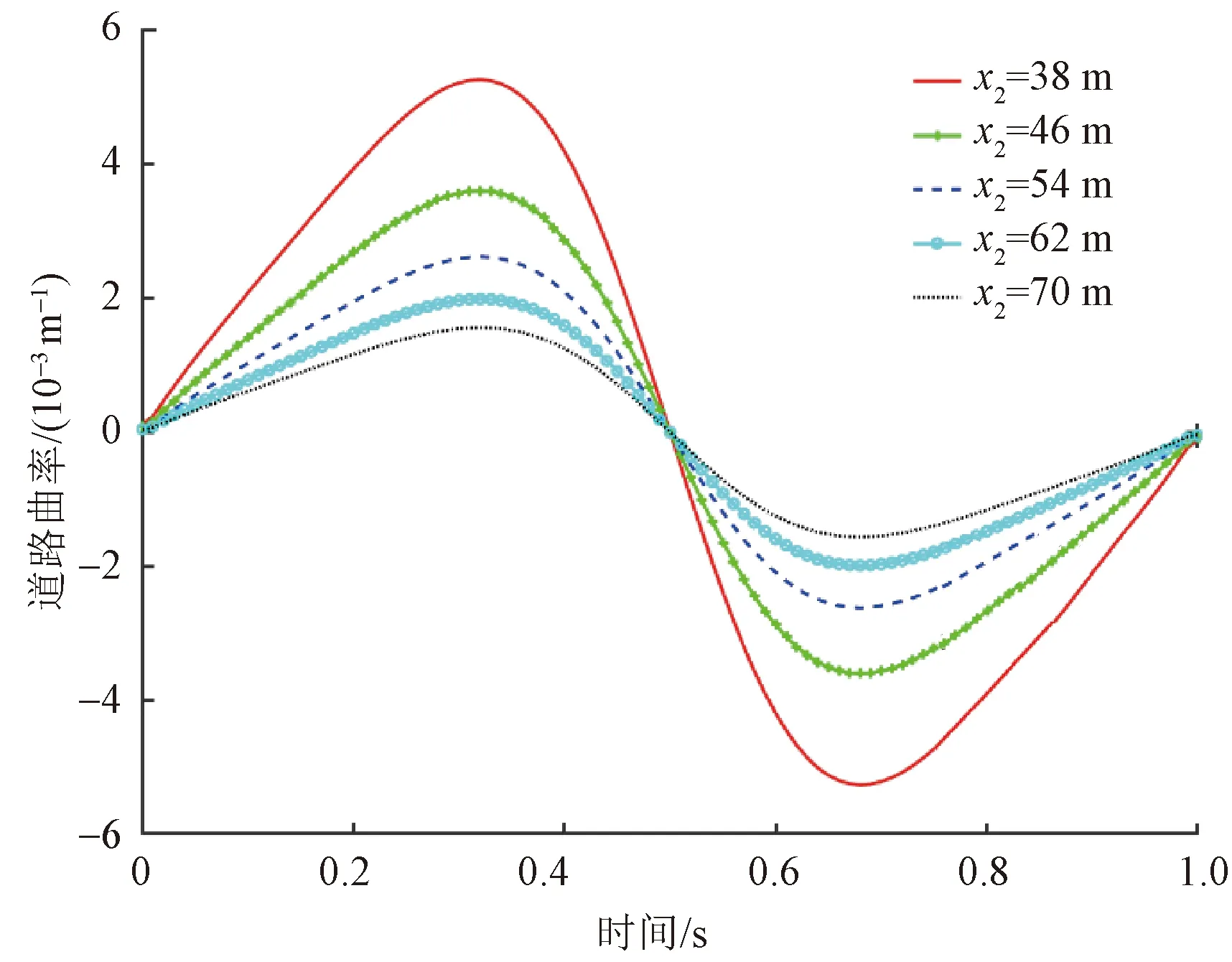
图9 不同x2点产生的轨迹曲线曲率Fig.9 Curvature of the trajectory curve generated by different x2 points

由图6～图9可知，相较于不同的x1点，不同x2点产生的轨迹曲线曲率变化范围更小，换道距离范围更大，对车辆跟踪影响更重要。所以，选择选取解最优x2点的方式来验证本方法对不同车速情况下前方出现障碍物的路径规划能力，进行如下仿真分析。

首先，利用MATLAB对算法进行仿真，本方法取具有代表性的3个道路速度，“低速”工况，速度设定为36 km/h；“中速”工况，速度设定为72 km/h；“高速”工况，速度设定为108 km/h。换道过程中允许的最大侧向加速度aymax=0.28gm/s2；车道宽度yd=3.75 m；车宽B=1.88 m；车长L=4.325 m；换道安全距离S=3v1，ω1=0.3，ω2=0.3，ω3=0.4，ω4=0，不考虑换道时间的影响。根据第3节所提出的边界条件及优化目标函数，得到对应不同车速下生成的轨迹曲线及曲线曲率，如图10和图11所示。

图10 不同车速规划轨迹曲线图Fig.10 Planned trajectory curves for different vehicle speeds

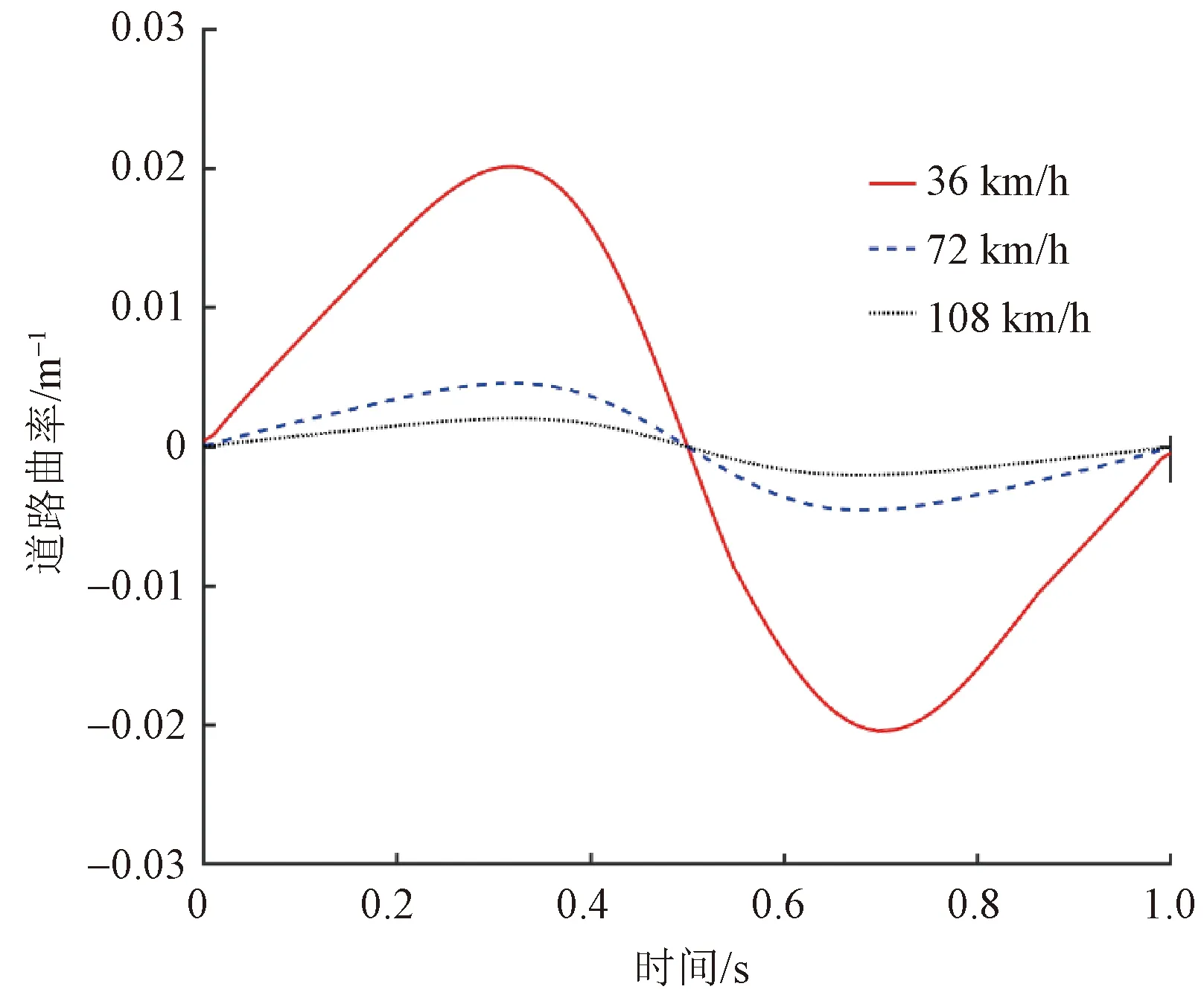
图11 不同车速规划轨迹曲线曲率图Fig.11 Curvature diagram of trajectory curves planned for different vehicle speeds

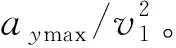
为验证此方法在后续实车上的应用是否有效，本文还利用车辆动力学软件CarSim与MATLAB/Simulink软件联合仿真，对所研究算法进行验证，自车车辆分别设置速度为36、72、108 km/h在正常双向直行道路行驶(道路中心线之间的距离为3.75 m)的工况来模拟避障过程。联合仿真实验采用CarSim软件自带的C-Class Hatchback作为实验车辆，此模型具体车辆参数如表1所示。

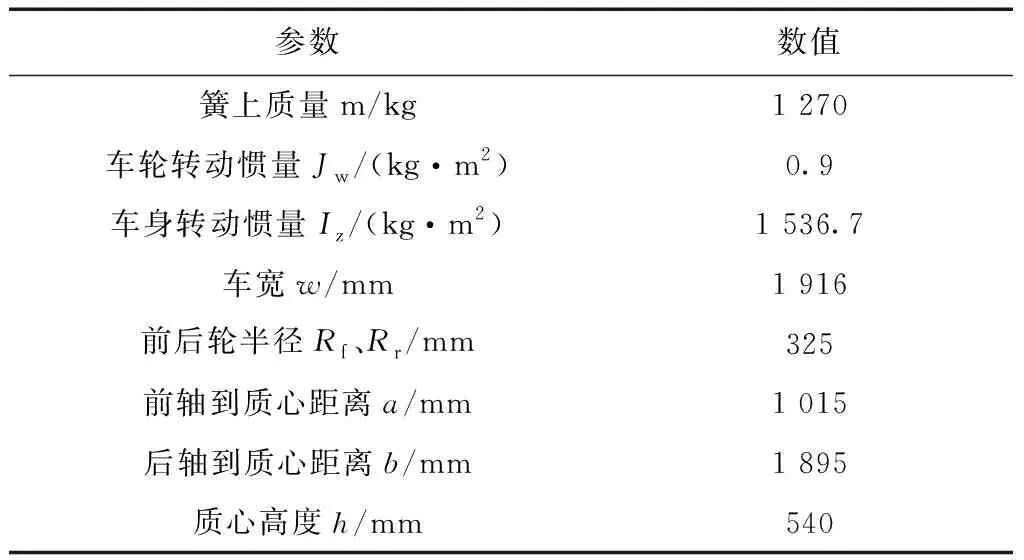
表1 实验车辆模型参数Table 1 Experimental vehicle model parameters

根据3种工况实验结果显示，无人车在避障过程中避障效果良好，轨迹跟踪偏差较小且实际车辆轨迹靠道路中心线；3种工况下车辆最大侧向加速度均在0.18g左右，小于侧翻阈值0.28g，满足车辆性能要求。

仿真效果如图12、图13所示。

图12 车速不同时轨迹跟踪效果图Fig.12 Trajectory tracking and at different speeds

(2)本文方法在无人车行驶过程中前方出现静止障碍物采用换道避障策略时，通过考虑车辆动力学性能极限和前车碰撞条件来规划无人车可行轨迹，所规划的最优换道轨迹曲线更加平滑，跟踪过程满足乘客乘坐舒适和车辆换道迅速的特点，为无人车采取换道避障策略时规划出了可行的换道轨迹。

图13 车速不同时侧向加速度图Fig.13 Lateral acceleration at different speeds

5 结论

综上仿真得到以下结论。

(1)基于五阶Bezier曲线规划的换道轨迹可以满足曲线在起始位置和终止位置曲率值为零的条件，车辆能够平稳跟踪轨迹行驶，且针对不同换道初始行驶速度，能够实现动态调整换道轨迹，突破了传统曲线插值局部路径规划法在换道前需要提前知道终止点位置的局限。

[1]中华人民共和国公安部. 2021年全国机动车保有量达3. 95亿 新能源汽车同比增59.25%[EB/OL]. (2022-1-11)[2022-1-15]. https: //app. mps. gov. cn/gdnps/pc/content. jsp?id=8322369.

Ministry of Public Security of the People’s Republic of China. In 2021, the number of motor vehicles in China will reach 395 million new energy vehicles increased 59. 25% year-on-year [EB/OL]. (2022-1-11) [2022-1-15]. https: //app. mps. gov. cn/gdnps/pc/content. jsp?id=8322369.

[2]赵安晨, 陈朋. 试论无人驾驶技术对城市道路交通及规划产生的影响与建议[C]//面向高质量发展的空间治理——2021中国城市规划年会论文集(6城市交通规划). 北京: 中国城市规划学会, 2021: 112-121.

Zhao Anchen, Chen Peng. Discussion on the influence of unmanned driving technology on urban road traffic and planning and suggestions [C]//Spatial Governance for High-quality Development： The Proceedings of 2021 China Urban Planning Annual Conference (6 Urban Traffic Planning). Beijing: Urban Planning Society of China, 2021: 112-121.

[3]熊璐, 康宇宸, 张培志, 等. 无人驾驶车辆行为决策系统研究[J]. 汽车技术, 2018(8): 1-9.

Xiong Lu, Kang Yuchen, Zhang Peizhi, et al. Research on behavior decision system of autonomous vehicle [J]. Automobile Technology, 2018(8): 1-9.

[4]Majumder S, Prasad M S, Shankar R. Three dimensional D*algorithm for incremental path planning in uncooperative environment[C]//International Conference on Signal Processing & Integrated Networks. New York: IEEE, 2016: 431-435.

[5]郑亮, 孙龙龙, 陈双. 一种改进工业自动导引车路径规划算法[J]. 科学技术与工程, 2021, 21(16): 6758-6763.

Zheng Liang, Sun Longlong, Chen Shuang. An improved path planning algorithm for industrial automatic guided vehicle [J]. Science Technology and Engineering, 201, 21(16): 6758-6763.

[6]张甫城, 胡敏, 江书真. 智能汽车换道轨迹规划曲线研究[J]. 汽车实用技术, 2021, 46(1): 26-28.

Zhang Fucheng, Hu Min, Jiang Shuzhen. Research on lane change trajectory planning curve of intelligent vehicle [J]. Automobile Practical Technology, 2021, 46(1): 26-28.

[7]彭晓燕, 谢浩, 黄晶. 无人驾驶汽车局部路径规划算法研究[J]. 汽车工程, 2020, 42(1): 1-10.

Peng Xiaoyan, Xie Hao, Huang Jing. Research on local path planning algorithm for autonomous vehicle [J]. Automotive Engineering, 2020, 42(1): 1-10.

[8]Latip N B A, Omar R. Feasible path generation using bezier curves for car-like vehicle[J]. IOP Conference Series: Materials Science and Engineering, 2017, 226(1): 012133.

[9]Xu L, Cao M Y, Song B Y. A new approach to smooth path planning of mobile robot based on quartic Bezier transition curve and improved PSO algorithm[J]. Neurocomputing, 2022, 473: 98-106.

[10]Bae I, Moon J, Park H, et al. Path generation and tracking based on a Bézier curve for a steering rate controller of autonomous vehicles[C]//International IEEE Conference on Intelligent Transportation Systems. New York: IEEE, 2013: 436-441.

[11]洪班豪. 汽车主动避障系统控制与仿真研究[D]. 长沙: 湖南大学, 2020.

Hong Banhao. Control and simulation research of vehicle active obstacle avoidance system [D]. Changsha: Hunan University, 2020.

[12]龚建伟, 姜岩, 徐威. 无人驾驶车辆模型预测控制[M]. 第2版. 北京: 北京理工大学出版社, 2020: 27-31.

Jianwei Gong, Yan Jiang, Wei Xu. Model predictive control for autonomous vehicle [M]. 2nd ed. Beijing: Beijing Institute of Technology Press, 2020: 27-31.

[13]张新锋, 陈建伟, 左思. 基于贝塞尔曲线的智能商用车换道避障轨迹规划[J]. 科学技术与工程, 2020, 20(29): 12150-12157.

Zhang Xinfeng, Chen Jianwei, Zuo Si. Intelligent commercial vehicle lane change and obstacle avoidance trajectory planning based on Bessel curve [J]. Science Technology and Engineering, 2020, 20(29): 12150-12157.

[14]Prautzsch H, Boehm W, Paluszny M. Bézier and B-spline techniques[M]. Berlin: Spring, 2017.

[15] Vahide B. Path planning for autonomous ground vehicles based on quintic trigonometric Bézier curve[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2021, 43(2): 1-14.

[16]Li H, Luo Y. Study on steering angle input during the automated lane change of electric vehicle: 2017-01-1962[R].Minneapolis: SAE Technical Paper, 2017.

[17]李洪硌. 无人驾驶汽车高速工况智能决策、轨迹规划与跟踪研究[D]. 广州: 华南理工大学, 2020.

Li Hongzuo. Research on intelligent decision-making, trajectory planning and tracking of unmanned vehicle under high-speed driving conditions [D]. Guangzhou: South China University of Technology, 2020.

[18]Farouki R T, Pelosi F, Sampoli M L. Optimization of corner blending curves[J]. Computer-aided Design, 2019, 117: 102739.

[19]Korzeniowski D, Laski G. Method of planning a reference trajectory of a single lane change manoeuver with Bezier curve[J]. IOP Conference Series: Materials Science and, Engineering, 2016, 148(1): 012012.

[20]游峰, 谷广. 面向无人驾驶的车辆协同换道轨迹规划[J]. 科学技术与工程, 2018, 18(15): 155-161.

You Feng, Gu Guang. Collaborative lane change trajectory planning for unmanned vehicles [J]. Science Technology and Engineering, 2018, 18(15): 155-161.

[21]Gill P E, Kungurtsev V, Robinson D P. A stabilized SQP method: superlinear convergence[J]. Mathematical Programming, 2017, 163(1-2): 369-410.