基于伍德沃德-劳森抽样方法的阵列平顶波束综合

王安义， 黄笑， 徐艳红

(西安科技大学通信与信息工程学院， 西安 710054)

天线是一种非常重要的无线电设备，有接收和发射能量信号的重要功能。世界上第一幅天线是赫兹在1887年为验证麦克斯韦预言电磁波的存在性而设计出来的。自无线电技术诞生以来，为满足高增益和强方向性，出现了阵列天线[1]，在1901年12月著名的跨大西洋无线通信实验中，古列尔莫·马可尼设计了一个由20个天线单元组成的阵列[2]。阵列天线是一类由不低于两个天线单元随机或按照一定规律排列组合而成的天线系统，通过改变其天线的幅度和相位来合成[3]。人们用方向图函数、方向性系数、主瓣宽度等参数来表征天线的方向性[4]，对理解天线的辐射特性有重要意义[5-7]。

随着天线应用越来越广泛，对其性能要求也越来越高[8]，人们希望天线主波束的形状可以综合设计成需要的形状。在卫星通信中，为了更好地利用有限的卫星资源，有时候就要求所对应的区域形状与辐射的波束形状尽量相配，以用来减少能量的损失。例如，雷达天线针状波束的宽度小，增益高，但所占的空间范围很小，因此适合有目标方向性的跟踪；具有余割平方波束形状且副瓣电平很低的阵列方向图，可以大面积覆盖主要区域，减少地面等干扰的负面影响。天线波束形成的目的就是求得一组效果最好的幅度和相位权值系数，这个求解过程被称为阵列天线的综合。波束形成技术在实际应用中具有很多商业和军事应用，文献[9]提出了一种基于群时延迟方法实现的接收模式波束形成器。文献[10]提出了一种可以消除干扰信号，保持阵列增益的滑动波束形成技术。阵列天线通过对激励电流的控制，可以降低天线的副瓣或使方向图形状更加接近理想方向图。文献[11]根据目标需求给出实现方向图的综合的实例，完成了对合成孔径雷达(synthetic aperture radar, SAR)天线方向图综合。波束赋形通过加权产生指向性的波束，从而可以得到高增益。由于波束赋形对空间提出的可选择性，在实际工程中应用的波束赋形技术可以达到不同的目的，文献[12]就设计了一款用于气象探测领域的高增益阵列天线。

在现代电子系统设计中，阵列天线的综合已成为其中一个重要的组成部分。伍德沃德-劳森抽样方法就是一种经典的方向图综合方法，通过在不同的离散位置上对所要求的远场方向图进行抽样，进而对线性阵列天线进行特定形状的波束综合，方法简单，抽样点少，运算速度快。文献[13]运用伍德沃德-劳森抽样法对阵列天线的方向图进行余割平方波束赋形。文中使用伍德沃德-劳森抽样方法对阵列天线进行波束综合，用MATLAB绘制出其方向图，使用控制变量法改变其参数，观察基本特性的变化情况。

1 波束赋形

波束赋形是通过控制激励电流的相位，使某处的信号增强或减弱，进而实现信号处理的一种技术。波束赋形既可以用在发射端，控制其激励的幅度和相位，达到控制其发射的信号强度的增强和减弱；也可用在接收端，把接收到的不同种类的信号重新以一种合适的规则组合起来，获得期望的信号幅度和相位。赋形波束有很多种形式，如平顶波束方向图、余割平方和超余割平方方向图等。

设期望方向图是一个关于θ=π/2对称的平顶(或扇形)波束，如图1所示，所对应的表达式为

(1)

式(1)中：S(θ)为指定角度区间上的预期方向图函数。

图1 平顶方向图Fig.1 Flat top direction

2 伍德沃德-劳森抽样方法

伍德沃德-劳森抽样方法被应用于波束赋形方面，是许多种方向图综合法中的一个。这一方法主要是通过从不同的离散角度进行抽样，根据所需的方向图，可以得到相应采样点的振幅，并得到各波束的加权值，从而得到所需的方向图。

假设有个一维阵列，由N个阵元组成，总长度为L，以阵元间距d沿着Z轴均匀排列放置(图2)其所对应的表达式为

(2)

式(2)中：an为激励系数；k为波数，k=2π/λ，λ=c/f；c为光速；f为工作频率；θn为抽样点角度。

总场的阵因子可以写成N项的叠加，其中N=2M或N=2M+1，M为取样点相关数，且每一项都具有式(2)的形式，则直线阵列(L=Nd)产生的阵列方向图表达式为

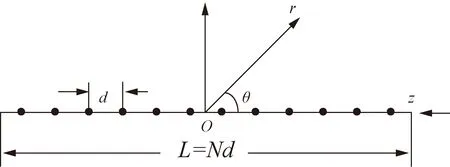
图2 等间距N阵元均匀直线阵列结构图Fig.2 Uniform linear array with equally spaced array N-elements

(3)

设给定的赋形方向图为f(θ)，则预期方向图S(θ)=f(θ)，在式(2)中等号的左边，则得到

an=S(θn)=f(θn)

(4)

如果在f(θ)的边缘上抽样，则有

an=0.5f(θn)

(5)

抽样点的位置θn=arccosxn，其中

(6)

式(3)所示的方向图归一化的各个单元的激励电流表达为

(7)

式(7)中：zm为单元位置。电流的作用就是联系各方向的抽样值。

无论奇数阵列(N=2M+1)还是偶数阵列(N=2M)，均有

zm={[m-(N+1)/2]d}，m=1,2,…,N

(8)

式(8)以坐标原点为中心来计算阵列单元的位置。

3 仿真实验

3.1 基于伍德沃德-劳森抽样方法的阵列平顶波束综合

以阵元数M=20，间距d=λ/2的均匀线阵为例，假设预给的期望方向图关于sinθ=0(θ=0)对称，用伍德沃德-劳森抽样方法对此阵列天线进行平顶范围X=0.4的平顶方向图综合。表1所示为满足平顶波束范围所对应的抽样位置和抽样值。

表1 平顶波束抽样点所对应的抽样位置和抽样值Table 1 Sampling position and sampling value corresponding to flat-top beam sampling point

表2所示为满足综合要求的情况下，所得到的各天线单元标号、阵元位置与激励电流的幅度和相位值的对应关系。

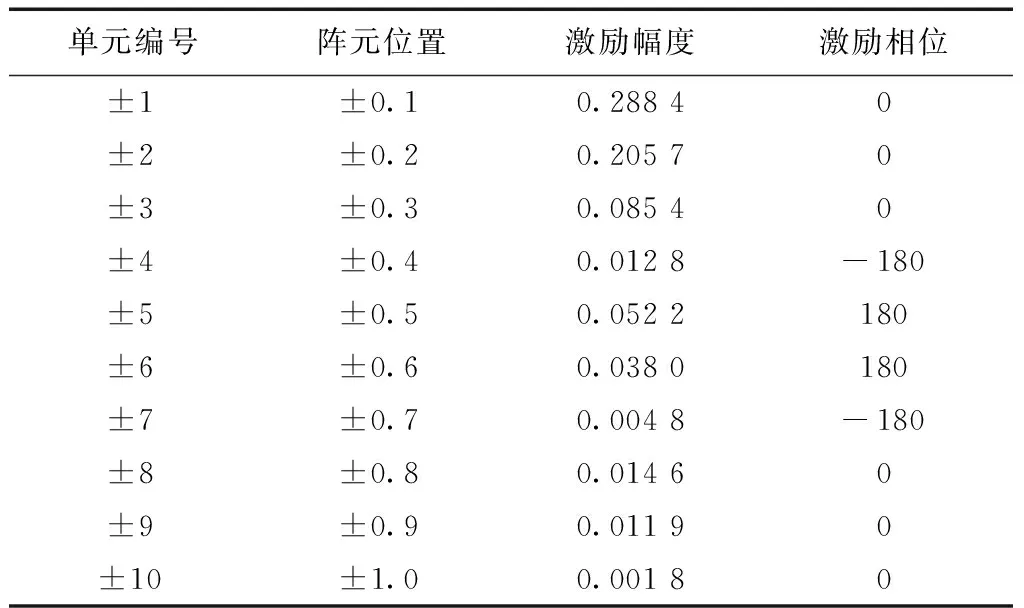
表2 阵列单元与激励电流的对应关系Table 2 Corresponding relationship between array element and excitation current

通过MATLAB软件进行仿真绘制，用伍德沃德-劳森抽样方法得到综合后的方向图如图3所示，在对应的|sinθ|≤0.4区域实现了平顶波束综合。根据所得阵列天线方向图的参数，得出表3综合前后阵列天线方向图的主瓣宽度和副瓣电平的参数值。

图3 平顶范围X=0.4时，用伍德沃德-劳森抽样法进行平顶波束赋形前后的对比图Fig.3 Flat-top beamforming with Woodward-Lawson sampling method in flat-top rangeX=0.4

结合表3和图3进行分析，可知：在规定区域|sinθ|≤0.4实现了平顶波束的综合，平顶区域的波纹起伏为0.18 dB，起伏范围小于0.2 dB，综合前阵列天线的旁瓣电平为-13.19 dB，综合后为-30.06 dB，其旁瓣电平降低了16.87 dB。

表3 阵列方向图的主瓣宽度和副瓣电平的值Table 3 Main lobe width and side lobe level of array pattern

3.2 改变阵元个数，对比综合结果

设均匀线阵的阵元间距为λ/2，预期方向图的平顶范围在|sinθ|≤0.4的区域。改变阵元个数M，分别绘制10阵元、20阵元、30阵元、40阵元时的天线方向图，如图4所示。

图4 不同阵元个数下的综合方向图Fig.4 Comprehensive pattern under different number of array elements

表4给出了不同阵列单元数时，综合前后阵列方向图的主瓣宽度和副瓣电平值。

表4 不同单元数时，综合前后的阵列方向图的主瓣宽度和副瓣电平的值Table 4 Values of main lobe width and side lobe level of array pattern before and after synthesis at different elements

观察得出，在阵元间距为λ/2，预期方向图的平顶范围在|sinθ|≤0.4不变的前提下，随着阵元数由10阵元、20阵元、30阵元、40阵元的增加，综合前的阵列天线的主瓣宽度逐渐缩小，而旁瓣数量也随着阵元数的增多而增多，综合前的副瓣电平稳定在-13 dB，而综合后的副瓣电平则在-30 dB左右，随着阵元数变多，阵列尺寸逐渐增大，抽样点越多，综合得到的方向图就越接近预期的方向图。

3.3 改变阵元间距，对比综合结果

设均匀线阵的阵元数为20阵元，预期方向图的平顶范围|sinθ|≤0.4。逐渐增加了阵元间距，使阵元间距d分别为λ/4、λ/2、3λ/4、λ时，用伍德沃德-劳森抽样方法综合出平顶波束形状的阵列天线方向图，如图5所示。

图5 不同阵元间距下的综合方向图Fig.5 The comprehensive pattern under different element spacings

结合图5和表5的数据可以看出，随着阵元间距的增大，主瓣宽度逐渐减小，逐渐出现了栅瓣，在阵元间距d<λ/2时，没有栅瓣，在阵元间距d>λ/2时，开始出现了栅瓣。

表5 不同阵元间距时，综合前后的阵列方向图的主瓣宽度和副瓣电平的值Table 5 Values of main lobe width and side lobe level of array pattern before and after synthesis with different array element spacing

3.4 改变平顶范围，对比综合结果

设均匀线阵的阵元数为20阵元，阵元间距d=λ/2，只改变预期方向图的平顶范围，使平顶范围|sinθ|≤0.2、0.3、0.5和0.7时，运用伍德沃德-劳森抽样方法绘制出平顶波束形状的阵列天线方向图，如图6所示。其方向图上的相关参数值见表6。

图6 不同平顶范围下的综合方向图Fig.6 Comprehensive pattern under different flat-top ranges

表6 不同平顶范围时，综合前后的阵列方向图的主瓣宽度和副瓣电平的值Table 6 Values of main lobe width and side lobe level of array pattern before and after synthesis with different flat-top ranges

从图6、表6可以看出，不论以平顶范围的值为多少来进行综合，综合后的副瓣电平都低于综合前方向图的副瓣电平，因此，可以得出相应地结论：伍德沃德-劳森抽样方法具有增加天线的方向性，降低副瓣电平的作用。

4 结论

以均匀线阵为例，用伍德沃德-劳森抽样法对阵列天线进行平顶波束赋形，用MATLAB软件绘制出综合前后的阵列天线方向图进行对比观察，同时使用控制变量法，通过分别改变其阵元个数、阵元间距以及平顶范围，观察其基本特性参数的变化规律，得到以下结论。

(1)用伍德沃德-劳森抽样方法进行阵列波束综合时，综合的线阵单元数越多，抽样点就越多，综合得到的方向图就越接近预期的方向图。

(2)用伍德沃德-劳森抽样方法对阵列天线进行综合后方向图主瓣范围内的波纹起伏范围明显减小，副瓣电平也明显降低。

(3)随着阵元间距的增大，阵列天线的主瓣宽度逐渐减小，并且逐渐出现了栅瓣。

(4)伍德沃德-劳森抽样方法具有增加天线的方向性，降低副瓣电平的作用。