基于模糊数学方法的直井分段压裂选层组合优化设计

王继伟, 曲占庆*, 李晓军, 郭天魁

(1.中国石油大学(华东)石油工程学院， 青岛 266580; 2.中国石化胜利油田有限公司东辛采油厂， 东营 247500)

目前中国大多数油田均进入开发的中后期，如何保持稳产增效是亟待解决的问题。保持油田稳产增效有着两条途径：一是改进生产开发技术，比如采用水力压裂技术进行储层改造[1-3]；另一方面为开源，例如开发动用难度大的低渗致密油气藏[4-7]。胜利油田经过五十多年的勘探开发，每年新发现储量中低渗及特低渗储量占比大，低渗及特低渗储量的效益动用是实现胜利油田资源接替的一个重要阵地[8-9]。东辛深层砂砾岩油藏是其重要组成，具有显著特征为：油藏埋深大，渗透率低；纵向上储层分布零散，油层跨度大；储层单层厚度较小，其平均厚度仅为1.4 m。

针对深层砂砾岩储层的特点，一次性笼统压裂难以实现效益开发，需要采取直井分段压裂，如何对层段进行划分和组合是关键。但是，目前现场对直井分段压裂的层段划分和组合，并没有形成完善的指导方法，大多依靠现场工程师的经验实施。开展深层砂砾岩油藏直井分段压裂选层组合技术研究，形成低渗透油藏直井多段压裂小层组合优化方法，对指导大跨度低渗透深层砂砾岩油藏的储层改造和实现其效益动用具有十分重要的意义。

当前学者对直井或者水平井分段压裂的决策研究大多集中在选井选层上，针对纵向跨度大的直井分段压裂选层组合的决策研究鲜有报道。刘长印等[10]针对低渗气藏水平井分段压裂选层问题，通过收集压裂层电性、物性、含油气性等参数，应用数理统计和模糊数学理论，计算选层系数来指导水平井压裂选层工作。沈澈等[11]采用最大值标准化法和层次分析法计算储层的综合评判值，对储层进行评价分级，指导致密砂岩储层压裂油井的快速选井选层。刘创新等[12]针对低渗-致密气藏的压裂选层问题，优选了影响压裂效果的关键地质和工程参数，采用级差变换和层次分析法计算得到可压性指数。另外，也有学者通过灰色关联、聚类分析、专家系统、神经网络等方法[13-17]来对压裂储层进行分析评价，指导分段压裂的选井选层。上述方法均需要人为打分计算权重，受主观因素影响较大，而且也需要大量统计数据用于算法模型的学习，才能达到较高精确度。TOPSIS (technique for order preference by similarity to an ideal solution)方法根据有限个评价对象与理想化目标的接近程度对评价对象进行排序，在现有的对象中进行相对优劣的评价。为了更简便同时也更客观准确地对储层进行评价，针对胜利油田深层砂砾岩直井分段压裂选层组合问题，运用直觉模糊多属性决策TOPSIS方法[18-19]，选取储层岩性、物性、含油性等参数，建立起分层组合评价模型，计算各小层的相对贴近度，进行分层组合设计。

1 直觉模糊多属性决策TOPSIS方法

模糊集理论是由Zadeh[20]教授于1965年创建的，直觉模糊集(intuitionistic fuzzy sets)是由Atanassov[21]在1986年提出的对模糊集理论的推广，模糊集是直觉模糊集的特殊情形。直觉模糊集对模糊现象的刻画同时考虑隶属和非隶属的信息，这样直觉模糊集在对模糊现象的刻画更加精确和全面，更能反映客观情况，因此直觉模糊集在工程技术界得到了广泛应用。部分学者将直觉模糊集从另一个方面进行扩展，即把讨论域的离散集合扩展到连续集合，提出了三角直觉模糊数。谭春桥等[22]把直觉模糊集与TOPSIS方法结合起来用于研究模糊多属性决策。

设X是讨论域，在X上的一个直觉模糊集A为

A={|x∈X}

(1)

式(1)中：映射μA:X→[0,1],νA:X→[0,1]满足条件0≤μA(x)+νA(x)≤1；μA(x)和νA(x)分别为x对直觉模糊集A的隶属度和非隶属度；πA(x)=1-μA(x)-νA(x)为x对直觉模糊集A的犹豫度。

1.1 直觉三角模糊数判断矩阵

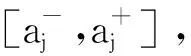
表1 模糊集与三角模糊数对应表Table 1 Correspondence between fuzzy sets and triangular fuzzy numbers

那么，指标Aj的直觉模糊隶属度和非隶属度可根据下式求得,即

(2)

(3)

式中：u和v分别表示Aj的最大和最小隶属度，0≤u≤1,0≤v≤1,u+v≤1，取u=0.8，v=0.1。

如此便得到了原始矩阵B=(P,Q)=[(pij)m×n,(qij)m×n]，其中P=[aij,bij,cij]为三角模糊数，Q=[μij,νij]为直觉模糊数。然后利用直觉三角模糊数加权几何平均算子将原始矩阵转换为综合判断矩阵。

三角模糊数的期望值为

H=(dij)m×n

(4)

dij=(aij+2bij+cij)/4

(5)

对象Si在属性Aj下的特征比重为

(6)

属性Aj的三角模糊熵权为

(7)

式(7)中：ej为三角模糊熵：

(8)

属性Aj的直觉模糊熵权为

(9)

式(9)中：Ej为直觉模糊熵：

(10)

则属性Aj的直觉三角模糊数加权几何平均算子为

(11)

根据式(11)计算结果，将每个对象的各属性值按下式进行相乘，得到综合评价值为

r′i=([a′i,b′i,c′i],μ′i,ν′i)

(12)

则综合判断矩阵为

(13)

1.2 TOPSIS方法计算相对贴近度

设r′1=([a1,b1,c1],μ1,ν1)，r′2=([a2,b2,c2],μ2,ν2)，则他们之间的Hanming距离[18]为

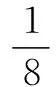
2|(1+μ1-ν1)b1-(1+μ2-ν2)b2|+

|(1+μ1-ν1)c1-(1+μ2-ν2)c2|]

(14)

正理想点为

i=1,2,…,m

(15)

负理想点为

i=1,2,…,m

(16)

(17)

(18)

2 分段压裂选层组合设计

2.1 分段压裂分段数的确定方法

进行分段压裂选层组合设计前，首先要解决储层分段压裂应分多少段的问题。考虑到不同地区地质情况以及现场压裂施工要求存在差异，特针对胜利油田东辛采油厂深层沙砾岩储层为目标，收集统计历年来该地区分段压裂成功井例的数据，见表2。通过分析分段数与储层纵向跨度之间的关系，总结出一个获得分段压裂分段数的经验方法。如图1所示，在直角坐标系中分别以储层纵向总跨度和分段数为横纵坐标轴，画出实施井例分布图。从图1中可以看出，井例近似呈线性分布，说明分段数与储层纵向跨度之间可以用线性方程描述。通过对数据进行线性回归拟合，得到一个分段数与压裂储层跨度的经验公式[式(19)]，可用于指导现场分段压裂施工设计合适分段数。

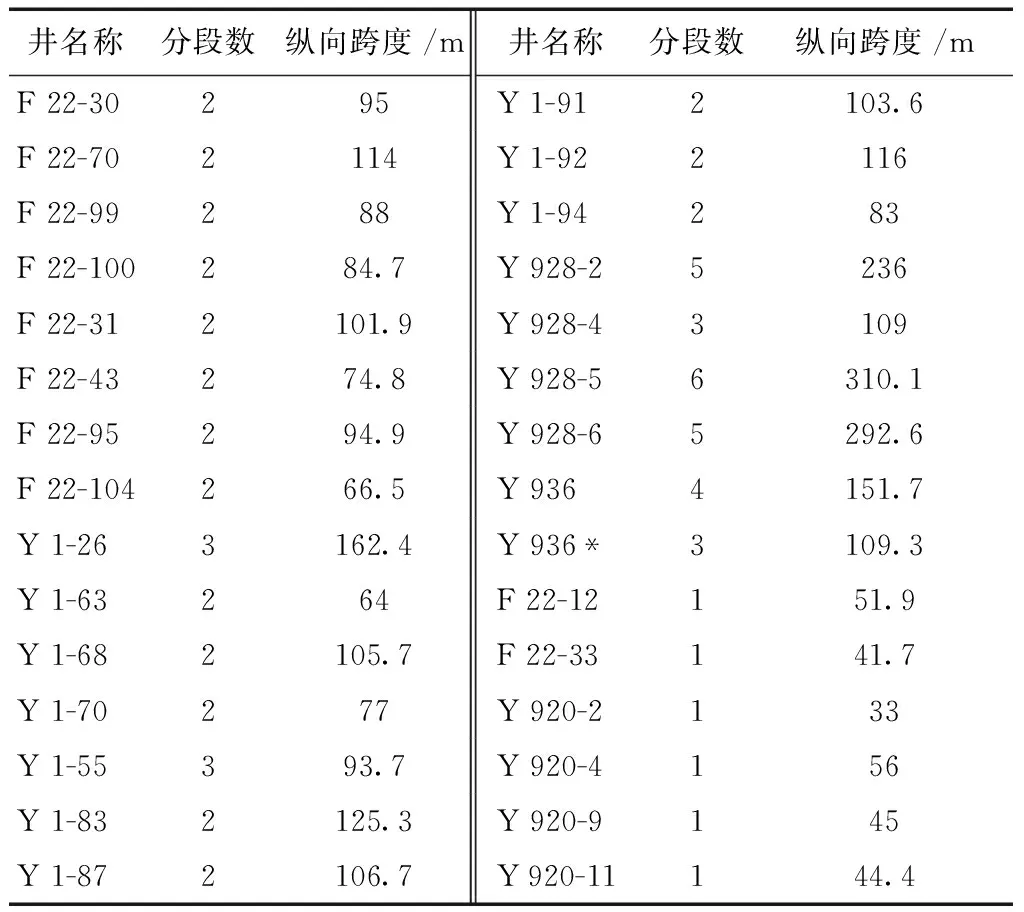
表2 分段压裂井例统计表Table 2 Statistical table of staged fracturing wells

图1 东辛砂砾岩油藏分段压裂分段数与储层纵向跨度关系Fig.1 Relationship between the number of staged fracturing stages and the longitudinal span in DongXin glutenite reservoir

y=0.017 7x+0.42

(19)

式(19)中：y为分层数，通过四舍五入取整；x为压裂层段总跨度，m。

2.2 分段压裂选层组合决策因素

深层砂砾岩储层分段压裂的分层组合设计受多方面因素的影响[23-24]，为了简化评价过程并保证评价结果能够代表储层综合性质和最终压裂效果，需要选择分段压裂选层组合的关键决策因素。首先，储层岩石力学参数和储层岩性特征对压裂施工以及压裂效果有着显著的影响，岩石的弹性模量和泊松比等参数会影响裂缝的起裂和扩展，同时在进行压裂的过程中，地层的压力会对裂缝的大小和深度造成一定的影响。储层的泥质含量和沙砾含量等岩性参数，对压裂施工有着重大影响，岩性差别过大的储层显然不能作为同一段进行压裂。其次，储层静态物性参数也是影响压裂效果的重要因素，静态物性参数主要包含渗透率、孔隙度、油气饱和度、储层厚度等。实验探究表明，渗透率越大，孔隙度越大，储层厚度越大，并且原始石油储量越多，则储层在进行压裂施工后油井可以高产的概率越大。

选择压裂储层弹性模量、泊松比、地层压力系数、泥质含量、储层解释、储层厚度、渗透率、孔隙度、油气饱和度作为关键决策参数，来评价各储层的综合性质。其中储层解释可以反映原始石油储量情况，而这一指标不是数值型数据，需要将其转换成数值，转换规则见表3。

表3 储层解释数值转换表Table 3 Numerical conversion table of reservoir interpretation

3 实例应用

以胜利东辛采油厂盐22-斜99井为例，进行分段压裂选层组合设计，该井共有15个小层，各层参数如表4所示。

表4 盐22-斜99井各小层评价参数Table 4 Evaluation parameters of each layer in Yan22-Xie 99 Well

由于各指标量纲不一致，需对指标进行归一化处理，即

(20)

对表4中数据进行处理，结果见表5。其中正向影响因素是指数值越大，对评价对象越有利的因素；负向影响因素是指数值越小，对评价对象越有利的因素。

表5 盐22-斜99井各小层无量纲化参数表Table 5 Dimensionless parameters for each layer of Yan22-Xie 99 Well

根据模糊集与三角模糊数的对应关系(表1)，可以得到各小层每个评价指标的三角模糊数，然后按照式(2)和式(3)计算直觉模糊数，该井的三角模糊数和直觉模糊数如表6所示。

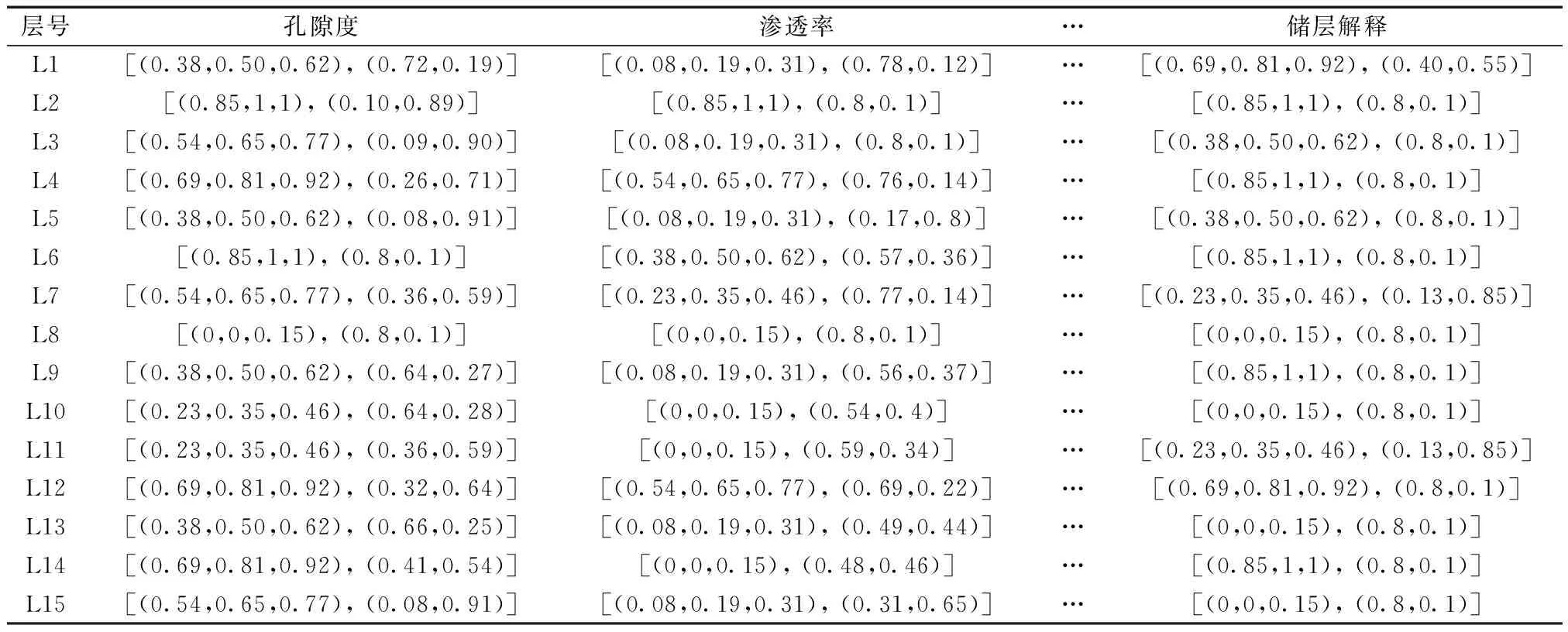
表6 各小层的三角模糊数与直觉模糊数Table 6 Triangular fuzzy numbers and intuitionistic fuzzy numbers of each layer

根据式(4)～式(12)计算直觉三角模糊数加权几何平均算子，最终得到综合判断矩阵,即

正负理想点分别为

表7 各小层相对贴近度结果Table 7 The relative closeness degree of cach layer

图2 根据相对贴进度进行的分段压裂选层组合设计Fig.2 Layer selection and combination for staged fracturing based on the relative closeness degree

4 结论

(1)通过对东辛深层砂砾岩储层分段压裂井例进行统计分析，得到了一个根据储层纵向跨度确定分段数的经验方法，可用于指导深层砂砾岩储层的分段压裂设计。

(2)针对东辛深层砂砾岩储层，选择了弹性模量、泊松比、地层压力系数、泥质含量、储层解释、储层厚度、渗透率、孔隙度、油气饱和度作为关键决策参数，应用直觉模糊多属性决策TOPSIS方法，构造综合评价矩阵，计算各油层的相对贴近度，以此进行分段压裂选层组合设计。该方法与传统评价方法相比，避免了主观人为因素的影响而能够客观准确地评价储层的综合性质。

(3)应用本文方法对盐22-斜99井进行了分段压裂选层组合设计，得到了与现场成功实施相一致的结果。利用定量方法解决了深层砂砾岩油藏纵向多薄互层的分段压裂选层组合问题，为建设智慧油田和保持油田稳产增效提供了技术支持。