变刚度机构及其在协作型机器人中的应用

曾宪湃 MORRISON Tyler 傅绎琳 苏海军

(俄亥俄州立大学机械与航空航天工程系 哥伦布 OH 43210)

1 引 言

智能辅助机器人与工人之间密切合作可以提高复杂生产的效率，该合作涉及人和机器人之间的物理交互，需要生产设备的精密设计[1]。与纯机器人装配或纯人工装配相比，混合装配(即机器人和工人共同执行搬运和/或装配任务的过程)具有更高的效率和更低的成本[2]。为了使协作型机器人与人类一起安全有效地工作，需要保证协作型机器人的灵活性和刚性。柔性结构保障了协作型机器人与人类工作的安全性，而刚性则是承载能力和较高运动精度的关键考量因素。现有研究表明，柔顺性更好的机械手臂对人类造成伤害的可能性更小[3-4]。为兼顾安全和性能，可通过在“慢速-刚性”与“快速-柔顺”[3,5]两种状态之间转换来实现，但刚柔转换的可控性仍具有挑战性[6]。

柔性机器人是协作型机器人研究的一个重要前沿领域。柔性机器人通常由纺织品和弹性体等材料制成，也可由任何具有高柔顺性的材料制成。由于高柔顺性材料具有柔顺性，且理论上具有无限自由度，因此，柔性机器人非常灵活耐用，不需要精密控制和环境识别，就可以避免损坏有效载荷或伤害人类[7-8]。

与传统机器人相比，柔性机器人价格更便宜、质量更轻且使用范围更广泛[9]，但高柔顺性也会产生局限。柔性机器人难以保持较高的定位精度，其自身的灵活性使其很难控制柔性机器人附属物的准确位置。此外，在外载荷作用下，柔性机器人往往会产生较大形变，无法达到传统刚性机器人的承载能力和加速度，从而限制了潜在用途。

由于柔性机器人性能的局限性，相关学者对可变刚度技术进行了研究。变刚度机器人可将柔性机器人的部分安全性优点与传统刚性机器人的高性能相结合。当需要更高的定位精度或承载能力时，变刚度机器人可以变得更加刚硬，但也可以变得更加柔顺，防止伤害周围的人或破坏环境。随着机器人与人类之间的互动变得越来越普遍，人们越来越关注可变刚度的安全性。对于具有辅助、康复和家庭角色的机器人来说，安全性是设计的关键考虑因素。与人类一起工作的机器人在得到广泛应用之前，必须解决安全问题，因此，可变刚度性能的研究受到了越来越多人的关注。

Blanc 等[5]基于固有特性变化对可控刚度机构进行分类，并提出改变截面二阶矩或改变结构的弹性性能的两种方法。Lavate 等[10]基于可变杠杆臂概念对变刚度制动器进行分类，扭转刚度可分为 3 种类型:通过弹簧位置的变化、通过力位置的变化或通过枢轴位置的变化控制传动比。

与纯刚性关节和纯柔性关节相比，变刚度关节因其刚度可调性而具有更好的环境适应性。Albu-Schäffer 等[11]提出了一种变刚度关节——通过改变弹簧的预压缩量来改变刚度的性能，这种变刚度关节提高了刚度的稳定性，但造成了能量损失。Choi 等[12]设计了一种应用于机械手臂的可变刚度关节，并提出了一种控制变刚度关节的刚度和位置的方案，兼具拮抗和变刚度的优点。就协作机器人应用而言，具有可变刚度连杆的机器人比具有刚性连杆的机器人更轻、更便宜且更安全。Zhu 等[13]结合杠杆和凸轮盘技术的优点提出了一种新的变刚度关节设计，通过改变枢轴的位置改变关节的刚度，并通过优化凸轮盘形状实现所需的渐进扭矩曲线，但调整刚度的速度较慢。

Jiang 等[14]提出一种基于粒状阻塞和膜片联轴器的可变刚度连杆机构；Hurd[15]介绍了一种基于层阻塞的可变刚度连杆机器人设计；Stilli等[16]将 Dragon Skin® 20A 硅胶与织物材料相结合，设计出了气动驱动的可控刚度连杆，其具有较大的刚度；Hao 等[17]基于气动人工肌肉设计了变刚度连杆；Ham 等[18]设计了一种三指变刚度抓手，通过拉动肌腱控制刚度，使用伪刚体模型确定设计参数，并开发了一种柔顺机构，可用于抓握各种类型的物体。

变刚度机器人具备刚性机器人所不具有的安全性特点，与柔性机器人相比，具有更好的承载能力和工作效率，能够适应复杂多变的工作环境。上述变刚度机构可应用于可穿戴机器人、康复机器人、假肢和步行机器人领域[19]。

随着材料学、控制学等学科的不断发展进步，变刚度机构领域已经实现了许多突破。但研究可变刚度的性能，对人机交互安全性的实现以及能量效率的提高仍然具有重要意义。尤其在安全性要求高以及复杂多变的工作环境中，可变刚度机构具有非常广阔的应用前景。

2 基于结构设计的变刚度方法

总结结构设计中几种常见的变刚度方法发现，结构刚度主要由两个因素决定:材料和结构设计。因此，变刚度原理主要集中在两个方面:(1)基于材料物理特性(如弹性模量)的变化；(2)基于几何结构或边界条件(如结构之间相互作用)的变化。

2.1 形状变形横截面

2.1.1 概念

形状变形横截面是指通过改变梁的横截面形状来改变刚度。如图 1 所示，She 等[20]提出的实验型样品(SM1)由 1 个舵机(Servo Motor)、4 对轴承架(Bearing Frame)、2 个万向传动轴(Universal Transmission Shaft)、2 个柔性梁(Flexible Beam)和 3 个绳驱动机构组成。实现横向刚度的关键是柔性梁，在柔顺状态(Compliant Mode)下，这些梁是平的，然而在刚性状态(Stiff Mode)下，它们会变成弯曲的形状。因此，柔性梁在横向载荷上具有更高的刚度，该原理与一张纸通过折叠的方式增加其刚度的原理相同。

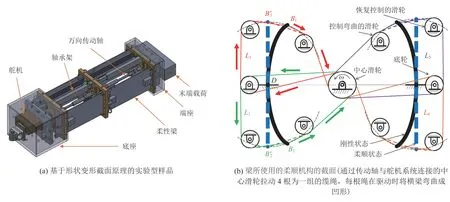
图1 SM1 的实验型样品及其梁中柔顺机构的横截面[20]Fig. 1 Cross section of experimental sample of SM1 and its compliant mechanism in beam[20]

单个固定导向形状变形梁的横向刚度k的计算公式如下:

其中，E为弹性模量；L为梁的长度；I为合适的截面二阶矩。由公式(1)可知，改变I会成比例地改变刚度大小。为了确定实现给定的刚度所需的驱动器位置，可应用经典梁理论确定由绳驱动机构的顶端挠度引起的梁的横截面形状变化，I可以通过对横截面进行积分来确定。

若柔性梁不能支持其他方向的载荷，那么实现变刚度是无效的，因此，She 等[20]增加了 4 个移动副轴承架连接绳驱动机构。将近端绳驱动机构固定在底座上，远端绳驱动机构安装在端座上。轴承架是允许移动副伸缩的直线导轨，轴承架和绳驱动机构之间通过转动副连接。实验结果表明，形状变形梁在横向可变刚度时表现为柔顺的平行导向机构，然而在垂直方向和垂直横向方向保持刚性。

为了使柔性梁均匀变形，3 个绳驱动机构沿着变形梁的长度均匀分布。为减少驱动机构的数量，She 等[20]设计了两个万向传动轴来配合 3 个绳驱动机构，底座中的舵机连接在轴上，可以同时驱动 3 个绳驱动机构。

如图 1(b)所示，柔性梁的中心线固定在绳驱动机构上，柔性梁的上下端与绳连接在传动系统上，使其向内拉弯成凹形。底座、端座、绳驱动机构和轴承架可视为刚性骨架部分，柔性梁可视为柔性部分。

2.1.2 结果

基于形状变形横截面原理的实验型样品(SM1)由弹性模量为 1.2 GPa 的塑料制成。在最柔顺的状态下，原型的刚度为 0.207 N/mm；在刚性状态下，实验型样品的刚度为 0.458 N/mm，可计算得出实验型样品的刚度比为 2.21。She 等[20]提出一种截面变形角的伪刚体模型，该模型与实验结果非常吻合。

图 2 为 She 等[21]研究中的另一种实验型样品(SM2)。在该研究中，四杆机构取代了绳驱动机构，其梁由相同的塑料制成，横向刚度变化范围为 0.540～1.936 N/mm，刚度比为 3.6。

图2 SM2 的实验型样品及其梁中柔顺机构的横截面[21]Fig. 2 Cross section of experimental sample of SM2 and its compliant mechanism in beam[21]

2.1.3 方法的优点和缺点

基于形状变形截面原理的实验型样品的优点包括:(1)控制——通过对刚度与变形传动角关系的建模以及对变形传动器的闭环控制，很容易实现刚度的控制；(2)响应时间——响应速度快且与舵机的功率直接相关；(3)可扩展性——通过改变材料类别、梁截面尺寸或长度，实现了刚度范围的可变。

基于形状变形截面原理的实验型样品的缺点包括:(1)机械复杂性——均匀分布变形梁所需的连杆和传动系统的机械复杂性会引起设计和质量方面的机械复杂性以及额外的失效点；(2)控制力——即使没有外部负载，驱动机构也需要通过施加力或扭矩使梁保持变形后的形状。

2.2 旋转梁构件

2.2.1 概念

图 3 为旋转梁构件(Rotating Beam Link，RBL)的实验型样品设计。在该构件中，4 个平行薄铝梁的每一端连接一个轮毂，轮毂中包含一个齿轮箱，用于旋转每个轮毂中带有舵机系统的梁。该设计通过旋转梁的方向来改变截面惯性矩，从而改变梁的扭转刚度。对于横截面为矩形且质心处于x-y坐标系的对称梁 ，其截面惯性矩 的计算公式如公式(2)所示:

图3 旋转梁构件的实验型样品设计[22]Fig. 3 Experimental sample design of RBL[22]

2.2.2 结果

本文团队曾展示了一种新型的可变刚度构件的实验型样品，其在极限位置之间的刚度比为 13.9，在中性结构和柔顺结构之间的刚度比为8.6[22]。然而，实验型样品的刚度比与理想状态下的理论值(刚度比为 122)之间存在显著差异。两种刚度比之间的差异是驱动系统中驱动旋转梁所必需的组件引入的寄生柔度产生的。

有限元分析表明，该构件的最大扭转刚度约为 19 N·m/rad，实验表明该杆可以承受 20 N 的轴向压力而不发生屈曲现象，也可通过在机械手臂的两个轮毂之间增加一个额外的机构提高扭转负载能力。

构件的横向刚度与梁的角度之间的模型计算了每个梁的柔顺性和屈曲，且能够精确地预测实验型样品的刚度性能。该模型可用于描述寄生柔顺性产生的影响并应用于之后的设计中。

2.2.3 方法的优点和缺点

RBL 实验型样品的优点包括:(1)控制——通过刚度和梁的角度之间的关系进行建模以及对梁的角度的闭环控制，很容易控制刚度比；(2)控制力——仅在外部载荷下才需要控制力来保持刚度；(3)响应时间——响应速度很快，梁只需要旋转 90°就能实现最大的刚度变化；(4)可扩展性——通过改变材料的选择和梁的横截面尺寸、长度或数量，就可实现刚度比和设计范围的缩放。

RBL 实验型样品的缺点包括:(1)机械复杂性——传动系统的机械复杂性使质量方面的复杂性增加并引起了寄生柔顺性，从而减小刚度控制；(2)屈曲——由于该设计依赖于 4 根细长梁，因此在特定的载荷状态下会出现弹性屈曲，从而增加刚度模型的非线性安定刚度控制复杂度。

2.3 平行导向臂上的滑块

2.3.1 概念

可变刚度滑块机械手臂结构是基于平行导向梁结构，由两端的挠性件以及两端挠性件之间的刚性连接部分组成，机械手臂刚度的计算公式如下:

其中，E为梁的材料的弹性模量；I为每个板的截面惯性矩；L为梁的有效长度。该设计的原理是通过改变平行导向梁的有效长度实现刚度变化。

基于此概念的第一个实验型样品如图 4[23]所示:该模型通过由丝杠和电动机(Motor)驱动的滚轮架改变梁的有效长度，从而实现刚度的变化。其机械手臂由两个平行的 7075 铝薄板挠性件(Al 7075 Sheet Flexure)组成；固定端(Fixed End)设计为电机和变速箱外壳；导螺杆(Power Screw)沿着滑块组装。为使两个挠性件产生弯曲，在自由端(Free End)添加一个带有凹槽的小螺母(Nut with Grooves)，其中包含作为滚动支撑的球形滚珠。随着滚轮架向自由端移动，挠性件的自由长度减小，由于支撑杆(Support Bar)具有高刚度，因此实验型样品的刚度增加。该实验型样品的外形尺寸为 406 mm×95 mm×104 mm，总质量为 952 g。

图4 丝杠驱动滑块的平行导向臂的实验型样品设计[23]Fig. 4 Prototype of the parallel-guided arm with screw driven slider[23]

图 5[24]为基于相同原理的第 2 个实验型样品——通过使用重量较轻、速度较高的气压缸来减少刚度变化的时间。为减少摩擦，托架(Carriage)沿着带有线性轴承(Linear Bearings)的支撑杆移动，仅在轴向与驱动器接触，且支撑杆承受所有横向载荷。通过与薄板接触的滚子轴承(Roller Bearings)施加边界条件。挠性件的自由端通过金属球滚动接触，允许其相对于圆柱体进行移动。机械手臂的外形尺寸为 450 mm×100 mm×100 mm，总质量为 450 g。

图5 气缸驱动滑块的平行导向臂的实验型样品设计[24]Fig. 5 Prototype of the parallel-guided arm with pneumatic cylinder driven slider[24]

2.3.2 结果

由电机和丝杠驱动的连杆滑块构件能够实现 20倍的刚度变化，静刚度的最大值为 10.049 N/mm，最小值为 0.500 N/mm。由气压缸驱动的连杆滑块构件可以实现 10 倍的相对较低的刚度变化，但可以在 0.6 s 内完成刚度变化，其最大刚度为3.407 N/mm，最小刚度为 0.358 N/mm。

2.3.3 方法的优点和缺点

通过改变平行导向梁的有效长度来实现刚度变化，其优点包括:(1)有效载荷——通过采用平行导向结构可以实现高的负载能力；(2)刚度范围(丝杠驱动)——采用丝杠驱动移动副的设计可使其刚度范围较广，动力丝杠轴具有非常大的刚度，当与平行导向梁完全结合时，可显著提高整体的刚度；(3)响应(气动驱动)——移动副在气压缸驱动时移动速度较快，从而可快速改变有效长度；(4)控制——刚度的控制与梁的有效长度直接相关。

通过改变平行导向梁的有效长度来实现刚度变化，其缺点包括:响应(丝杠驱动)——由螺杆和电机驱动的滑块的移动速度与螺杆螺距、电机功率有关，具有更高功率的电机通常体积庞大且价格昂贵，从而限制了整体响应时间，增加了连杆的质量；控制力——当连杆偏转时，需要额外的控制力来移动滑块。

2.4 平行导向臂的层阻塞

2.4.1 概念

本小节将介绍一种平行导向机械手臂，其通过气动驱动层阻塞实现了 75 倍的较大刚度比[25]。图 6(a)为平行导向臂的基本结构，该机械手臂由两个 3D 打印的柔性梁组成。将两根柔性梁平行放置，使机械手臂能承受更多由末端约束引起的弯矩，与单根梁相比，其具有更高的垂直载荷能力，从而得到刚性部分和柔性部分相互连接的新型截面。如图 6(b)所示，沙漏形刚性部分之间通过相对较长和较薄的柔性部分连接，该新型设计的梁虽然较厚，但仍具有较好的柔顺性。图 6(c)为阻塞层的交错分布。在梁两侧沙漏部分的顶部设置阻塞层(Jamming Layers)，绿色层连接梁的左端，黄色层连接梁的右端。绿色层和黄色层被均匀打乱，从而使各层交叉分布。阻塞层施加的摩擦力增加了梁的厚度，从而增强了层阻塞的作用。

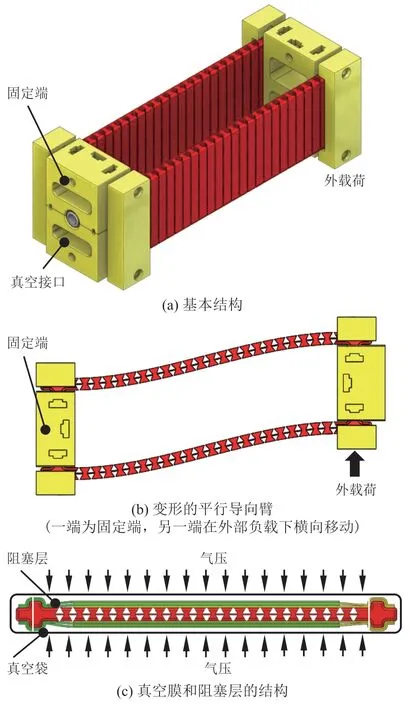
图6 运用层阻塞方法的平行导向臂的设计[25]Fig. 6 Design concept of the parallel-guided arm with layer jamming[25]

2.4.2 结果

机器人手臂从初始位置偏转到 20 mm 的末端挠度的过程中，收集其力和挠度的数据，数据的收集是以 17 237.5 Pa 为增量，从 0 Pa 增加到86 187.5 Pa。实验结果如图 7 所示，在给定的真空压力下，平行导向臂的刚度由呈线性增加变化至非线性增加，且非线性增加的速度较为缓慢。当末端挠度达到 20 mm 时，刚度达到饱和。在卸载过程中，由于柔性骨架中存储有应变能，因此，机器人手臂趋于恢复到其初始位置。

图7 平行导向臂的载荷-挠度测量与层阻塞[25]Fig. 7 Load-deflection measurement of the parallel-guided arm with layer jamming[25]

在 0 Pa 的真空压力下，手臂刚度被定义为基本刚度，其表示中心骨架的柔韧性，作为计算刚度变化比的分母。随着所施加的真空压力的增加，刚度也在不断增加。刚度变化比即真空压力为 86 187.5 Pa 时所对应的刚度除以基本刚度。实验表明，该原型的刚度比为 75，最小刚度和最大刚度分别为 0.080 3 N/mm 和 6.05 N/mm。

阻塞层的快速驱动也是一个重要的设计考虑因素。为快速去除真空袋中的空气，本文团队重新设计横梁内部特征的通道以促进排气。内部空气通道可通过 3D 打印制造，不需要额外的制造过程。另一种快速产生真空的方法是使用真空发生器。常规电机真空泵的流量为 0.056 6 m³/min左右，少数可达 0.283 2 m³/min。然而，气动真空发生器的流量可以达到 0.849 5 m³/min，可显著提升真空度的调节性能。利用真空发生器，阻塞层可以在 0.25 s 内完全驱动。

可变刚度层阻塞方法已应用于结构变形和设计机器人抓手。图 8(a)的实验型样品[26]既能通过气动肌肉改变机器人抓手的曲率，又能改变其刚度。与之前的柔性机器人变形结构相比，将McKibben 驱动器集成到 3D 打印的结构中，可实现更高的承载力，此外，该设计可实现的最大刚度变化为 75。图 8(b)所示为层阻塞与绳驱动的柔顺机构相结合的具有可调节刚度的机器人抓手[27]，其刚度和承载能力均有显著性的提高，分别增加了 24 倍和 30 倍。

图8 层阻塞方法的应用Fig. 8 Applications of layer jamming

2.4.3 方法的优点和缺点

层阻塞方法的优点包括:(1)有效载荷——采用平行导向结构，承载能力较强；(2)机械复杂性——设计简单紧凑，运动部件少；(3)响应——采用特定的设计和选择特定的部件，可以促进快速排气以及调节真空压力；(4)可扩展性——通过改变梁的尺寸、层的材料和阻塞层数来改变刚度范围和刚度比。

层阻塞方法的缺点包括:(1)建模——由于存在滞后现象，建立无负载时的分析模型较为困难；(2)控制——由于使用高流量真空发生器，需要运用复杂的压力控制算法和硬件设计。

3 讨论与分析

表 1 对比分析了结构设计中几种常见的变刚度方法，并对其属性进行量化。图 9 为每种方法在刚度和响应时间方面相对优势和劣势的可视化表达。值得注意的是，在不同的实验型样品之间，并非所有的设计参数都保持不变，不同装置之间的质量、长度、材料等属性都略有不同，这会影响可变刚度的性能，导致难以比较这些装置的性能，但仍可得出一些普遍的结论。

图9 4 种可变刚度方法的刚度比、刚度范围和响应时间的比较Fig. 9 Comparison of the stiffness ratio, stiffness range and response time for tunable stiffness solutions

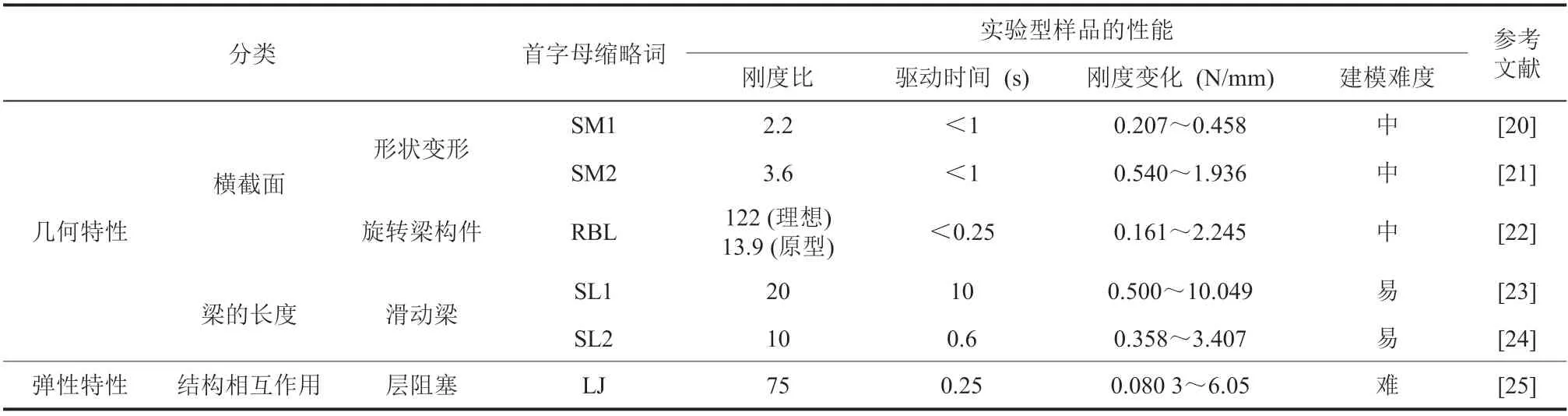
表1 可变刚度方法的比较Table 1 Comparison of variable stiffness methods

在响应时间方面，形状变形梁、旋转梁、气动气缸驱动滑块、层阻塞等设计方法响应速度较快。形状变形梁和旋转梁方法通过选择足够的电机和驱动机构进一步优化响应时间，但增加驱动机构的复杂性会对刚度比和质量产生负面影响。在运动部件的数量和紧凑性方面，气缸驱动滑块和层阻塞方法有一个相对简单的配置。与丝杠驱动的滑块相比，气缸驱动的滑块在直线导轨上的移动速度较快，可实现性能的显著提升。层阻塞方法的响应时间与需要排出的空气量、流体系统中的阻力和泵的性能有关，可采用紧密的真空袋、嵌入内部空气通道或高流量真空发生器优化响应时间。然而，还需要设计有关控制的方案才能快速而精确地调节压力以进一步优化响应时间。

在结构设计的变刚度方法中，层阻塞方法具有最佳刚度比。其值取决于相对较高的最大刚度(在任何机械连杆中没有寄生柔顺性损失)和相对较低的最小刚度。层阻塞方法的刚度比取决于梁的尺寸、梁和阻塞层的材料选择、阻塞层层数及可用真空度。为实现最佳刚度比，需要建立一个综合的分析模型并进行大量实验。基于形状变形概念的构件需要较高的线张力或连杆弯曲应力才能达到较高的刚度比。对于旋转梁构件来说，它具有实现更大刚度变化的潜力，但设计出一个更安全的梁边界条件仍具有挑战性。基于使用滑块的有效长度变化的连杆还需要改进滑块机构，以便在横梁上提供大而安全的夹紧力。

层阻塞方法具有独特的优点，它可通过简单地增加或减少真空压力来改变构件在外载荷作用下偏转的刚度，若使用其他方法，构件则很难在外载荷作用下改变刚度的大小。旋转梁构件上的线和连杆驱动机构以及舵机需要更大的电机扭矩使预加载梁变形或驱动。同样，在偏转的平行导向梁上移动的滑块也需要克服更大的阻力。

为验证基于平行导向臂设计的层阻塞方法的变刚度能力及其稳定性，Zeng 等[25]构建了有限元分析模型。由于沙漏形截面的刚度远高于较薄的柔性部分的截面刚度，因此，所有的沙漏形部分设置为具有刚性的性能。通过对柔性部分、阻塞层和真空膜使用壳单元进行建模，基于对柔性梁、阻塞层和真空膜中应力收敛性的研究，将有限元分析中的网格大小设置为 2 mm。在骨架与底部阻塞层之间、阻塞层之间以及最外阻塞层与其对应的真空膜之间存在摩擦，通过测量可知该摩擦系数为 0.167。为计算摩擦力的大小，Zeng等[25]运用了增强拉格朗日方法。通过有限元分析，可以得到层之间在施加外部负载时的相关运动、法向弹性应变的分布，与法向应变相比，剪切应变较小。为验证平行导向臂设计的垂直稳定性以及扭转稳定性，通过对单板结构、双板结构以及双板间带有加强筋的结构进行有限元建模与分析，可以得到梁的厚度、梁的距离对临界垂直屈曲载荷以及扭转刚度的影响。通过比较这 3 种结构的有限元分析结果可知，基于平行导向臂设计的层阻塞方法具有较高垂直稳定性和扭转稳定性方面的优点[25]。

基于机械结构设计的变刚度机构较为复杂、体积较大、整体设计较为笨重且所需驱动时间较长。基于材料特性的变刚度机构性能不稳定，如热敏材料(形状记忆材料)通过相变改变其刚度，但这一转换需要较长的时间来吸收和释放热量，驱动效率较低且具有不可预测性。基于层阻塞方法的变刚度机构质量较轻、安全可靠、刚度变化较快、结构简单且易于制造，可通过较小的体积变化实现较大的刚度变化。层阻塞方法所具有的刚度可变性较易运用于各种应用中，如用于抓握物体、末端执行器的设计以及增强结构的抗震性等，因此，基于层阻塞方法的变刚度机构具有较为广阔的应用前景，未来变刚度机构可基于层阻塞的设计方法进行研究和改进。

4 结 论

本文对基于改变结构刚度的设计方法进行了讨论，但这些设计还需要额外改进才能转化为成熟的技术。层阻塞方法具有刚度比高、刚度范围大、施加气动压力控制时响应速度快等特点；丝杠驱动滑块方法较为简单，但响应时间较慢；气动驱动滑块的方法响应速度快，但需要复杂的控制算法才能实现；基于可变横截面的方法具有良好的刚度比和响应速度，但机械结构复杂。未来可通过应用其中一个或者多个概念设计方法解决可变刚度的实际工程问题，如多段机械手臂通过迭代的方法[16]可以改进原型设计及其性能。