借助数学实验 实现深度学习
2022-12-17吴秀兰
吴秀兰
(江苏省常州市武进区坂上初级中学 213100)
初中数学教学中应注重借助实验引导学生进行深度学习,鼓励其参与到数学知识学习中,使学生自己发现问题、探究问题、得出结论,如此不仅能很好地提升其学习体验,而且可以留下深刻印象,更好地把握数学知识的外延.尤其对于部分数学结论教学中,借助数学实验,更容易使学生搞清楚结论成立的条件以及适用的问题情境,避免其死记硬背,张冠李戴.
1 情境铺垫
二次函数是初中数学的重要知识点,尤其有关二次函数图像方面的知识是日常测试以及中考的热门考点.为加深学生对二次函数图像的认识,并能以二次函数图像为基础,掌握特殊函数图像的画法,提高运用数形结合知识解题的意识与能力,课堂上为学生展示如下情境:
运用多媒体技术为学生展示二次函数y=x2-2x+3,要求学生回答以下问题:求该二次函数的顶点坐标以及对称轴;判断方程x2-2x+3=0是否有实数根;画出二次函数的图像.学生积极联系所学对二次函数进行变形可得y=x2-2x+1+2=(x-1)2+2,可以看到二次函数的顶点坐标为(1,2),对称轴为直线x=1.对于方程x2-2x+3=0,因Δ=4-4×3=-8<0,因此,该方程并没有实数根.令x=0,可得y=3,其关于对称轴对称的点的坐标为(2,3),由此,不难画出y=x2-2x+3的图像.
课堂上要求学生回答上述问题,既巩固其所学的二次函数图像知识,又能为接下来的实验开展奠定坚实基础.
2 实验开展
实验情境一:待学生画出二次函数y=x2-2x+3的图像后,提出以下实验问题,要求学生思考、探究:画出-y=x2-2x+3的图像,思考其和二次函数y=x2-2x+3的图像有什么关联?你能得出什么结论?
对-y=x2-2x+3进行变形得到y=-(x2-2x+3)=-(x-1)2-2,显然其顶点坐标为(1,-2),图像和y轴的交点为(0,-3),该点关于对称轴对称的点为(-2,-3),由此学生不难画出该二次函数的图像.
而后要求学生将两个函数图像放在同一平面直角坐标系中,观察两个函数图像的联系.学生经过认真观察与讨论容易得出两个函数图像关于x轴对称.
实验情境二:课堂上给学生展示二次函数y=x2+2x+3,要求学生画出该二次函数图像,思考其与y=x2-2x+3图像、-y=x2-2x+3图像之间的联系.同样y=x2+2x+3=(x+1)2+2,其顶点坐标为(-1,2),对称轴为直线x=-1,图像和y轴的交点为(0,3),其关于对称轴对称的点为(-2,3),则容易画出其图像.
观察可知二次函数y=x2+2x+3的图像和二次函数y=x2-2x+3图像关于y轴对称,和-y=x2-2x+3的图像关于原点对称.
实验情境三:在屏幕上展示y=x2-2|x|+3,要求学生联系所学,结合上述情境积累的经验画出其图像,思考该函数图像的对称轴是哪一条直线?
因该二次函数中带有绝对值,结合所学的绝对值知识可知,x的正负不确定.因此,需要进行分类讨论,即,当x≥0时,y=x2-2x+3;当x<0时,y=x2+2x+3,则该函数的图像是由两个函数图像构成,分别取y=x2-2x+3图像中x≥0的部分和y=x2+2x+3图像中x<0的部分,得出其图像.由图可清晰地看到,函数图像关于y轴对称.
实验情境四:已知方程x2-2|x|+3=t,探讨该方程根的个数.解答该题可采用转化思想,将其看成:y=x2-2|x|+3,y=t两个函数图像的交点个数即为方程根的个数.由图像可知函数的最小值为y=2,其和y轴的交点的纵坐标为3.显然其分以下四种情况:
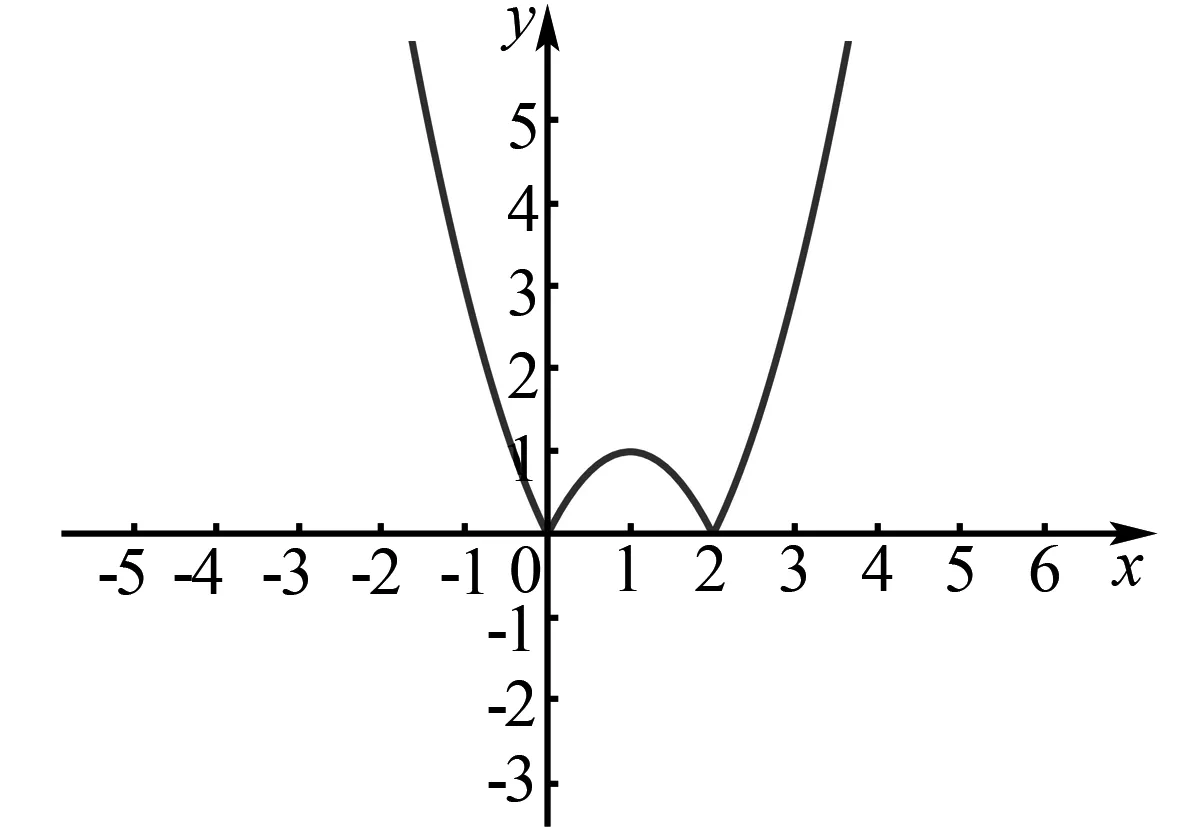
当t<2时,方程x2-2|x|+3=t无实根;当t=2或t>3时方程x2-2|x|+3=t有两个实根;当t=3时,方程x2-2|x|+3=t有三个实根;当2 实验情境五:画出函数y=|x2-2x+3|的图像,思考其与y=x2-2x+3图像有什么关系?为什么? 学生通过画图探究,不难回答提出的问题.因二次函数y=x2-2x+3的开口向上且最小值为2.无论x取任何的实数,y>0均成立,则函数y=|x2-2x+3|的图像和函数y=x2-2x+3图像相同. 继续抛出如下问题,要求学生思考探究:二次函数y=x2-2x是由二次函数y=x2-2x+3怎样移动而来?分别画出二次函数y=x2-2x和y=|x2-2x|的图像.由二次函数图像平移规律可知,要想得到二次函数y=x2-2x需要将二次函数y=x2-2x+3上的各点向下平移三个单位.令x2-2x=0,可得x1=0,x2=2,可知该函数图像和x轴的交点分别为(0,0),(2,0)且对称轴为直线x=1,如此便不难画出其图像.但是怎样画出函数y=|x2-2x|的图像呢? 图1 课堂训练:实践中为检验学生是否真正地理解实验内容,课堂上展示如下习题,要求学生思考作答: 已知关于x的方程|x2+ax|=4有4个不相等的实根,则a的取值范围是( ). A.a<-4或a>4 B.a=4或a=-4 C.-4 解答该题可先画出函数y=x2+ax的图像,而后将y<0部分以x轴为对称轴翻折到x轴上方,画出函数y=|x2+ax|图像, 观察图像可得选择A项.从解题过程来看,学生只有真正地吃透数学实验内容以及实验结论,才能迅速找到解题思路.通过该课堂训练习题,可暴露出学生在数学实验中的不足,启发其结合自身实际情况及时查漏补缺. 课堂上组织学生开展数学实验,得出以下结论:对于二次函数y=ax2+bx+c(a≠0),使用“-x”替换其中的“x”得到二次函数y=ax2-bx+c,两个函数图像关于y轴对称;使用“-y”替换其中的“y”得到二次函数y=-ax2-bx-c,两个函数图像关于x轴对称;使用“-x”、“-y”替换其中的“x”、“y”得到二次函数y=-ax2+bx-c,两个函数图像关于原点对称;图像中y>0的部分和二次函数y=|ax2+bx+c|图像一样.图像中y<0的部分需要将其关于x轴对称得到y=|ax2+bx+c|图像;判断方程根的个数的问题时可采用数形结合思想,结合方程特点,将其拆分成两个函数,参考上述结论画出函数图像.图像交点个数即为方程根的个数. 其一,做好实验铺垫.为使学生做好数学实验的心理以及知识准备,在进行实验之前应做好铺垫,注重从学生熟悉的知识切入,创设相关的问题情境,更好地激发学生参与数学实验的兴趣与积极性.在铺垫环节应注重设计问题,要求学生积极联系所学思考作答,使其主动地回顾已学知识,为实验的开展埋下伏笔. 其二,注重循序渐进.设计数学实验时应注重遵循学生的认知、学习规律,合理把握数学实验问题的难度,循序渐进,逐步深入,如此可避免学生出现畏难情绪,使其以高涨的热情投入到数学实验中.实践中按照由易到难的原则设计问题要求学生进行实验、探究,很好地满足了学生的心理预期,尤其当学生得出正确的探究结论时,成就感油然而生,在课堂上表现得更为积极、活泼.不仅如此,在完成数学实验后要设计课堂训练习题,要求学生作答进一步夯实其所学. 其三,给予启发、引导.对于部分学生而言围绕实验开展深度学习活动可能具有一定难度.为保证学生向着正确的方向思考问题,降低其实验探究难度,提高数学实验的成功率.学生实验过程中,教师应注重走下讲台了解学生的探究进度、探究思路,必要情况下使用多媒体技术给予引导,或者提出问题给予启发,使其能够顿悟,及时调整探究思路. 其四,重视实验总结.完成数学实验后应注重引导学生做好实验结论的总结,使其在以后解答相关数学习题时能够灵活应用,提高解题效率.同时,要求学生思考,实验结论的使用情境以及应用结论时应注意哪些细节等.实践中专门给学生预留实验总结时间,并鼓励学生相互交流心得,交换课堂笔记等,确保总结的内容能够涵盖所有实验内容,避免有知识上的漏洞.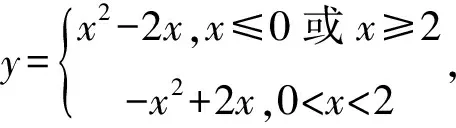
3 实验结论及教学启示
3.1 数学实验结论
3.2 借助数学实验进行深度学习的启示
