航天器轨道追逃博弈多阶段强化学习训练方法

袁利，耿远卓，汤亮，黄煌

航天器轨道追逃博弈多阶段强化学习训练方法

袁利1，2，耿远卓1，2，汤亮1，2，黄煌1，2

（1.北京控制工程研究所，北京 100094；2.空间智能控制技术重点实验室，北京 100094）

针对航天器轨道追逃博弈问题，提出一种多阶段学习训练赋能方法，使得追踪星在终端时刻抵近逃逸星的特定区域，而逃逸星需要通过轨道机动规避追踪星。首先，构建两星的训练策略集，基于逻辑规则设计追踪星和逃逸星的机动策略，通过实时预测对方的终端位置，设计己方的期望位置和脉冲策略，显式给出追逃策略的解析表达式，用于训练赋能；其次，为提升航天器的训练赋能效率及应对未知环境的博弈能力，提出一种基于强化学习技术多模式、分阶段的学习训练方法，先使追踪星和逃逸星分别应对上述逻辑规则引导下的逃逸星和追踪星，完成预训练；再次，开展二次训练，两星都采用邻近策略优化（PPO）策略进行追逃博弈，在博弈中不断调整网络权值，提升决策能力；最后，在仿真环境中验证提出的训练方法的有效性，经过二次训练后，追踪星和逃逸星可有效应对不同策略驱动下的对手，提升追逃成功率。

轨道追逃；博弈决策；强化学习；训练赋能；多阶段学习

0　引言

随着航天技术的发展，各国航天器智能化程度不断增加，在传统制导、导航与控制（Guidance， Navigation， and Control， GNC）技术基础上，逐渐朝向智能感知、类人决策、精准控制的方向发展。同时，太空环境日益复杂，在轨航天器数量指数增长且能力大幅提升，传统依靠地面指控的模式难以应对时敏空间任务［1］。此外，目前星上GNC系统主要面向确定性任务场景，智能化水平较弱，在强不确定性的博弈态势下中缺乏自主决策能力，而智能决策依赖于前期大规模地面训练及星上二次训练。因此，提升训练效率对于航天器智能化发展至关重要，可有效降低研制周期，节省计算资源。本文将针对轨道追逃博弈提出一种高效的训练赋能方法。

航天器追逃作为太空博弈的典型场景，充分体现了轨道运动特性，诸如交会对接、在轨操控等任务皆可抽象为轨道追逃问题，因此吸引了众多学者研究［3］。追逃任务中，追踪星和逃逸星的目标相反，追踪星旨在尽快抵近到逃逸星的特定区域，而逃逸星需要躲避追踪星。目前，对于追逃问题的研究主要集中在飞机、导弹［4］、无人机［5］等近地领域，例如空战博弈Alpha Dog Fight［6］。而对于太空中的航天器追逃问题，由于受到地球引力约束和自身燃料约束，其侧重点及求解思路和方法有所不同，需要充分利用轨道动力学特性，保证燃料高效完成追逃任务。

针对航天器追逃的赋能问题，主要分为3种方法：

1）赋能方法立足于轨道动力学，通过深入分析航天器轨道运动规律，根据航天器当前速度，实时解算和预测航天器未来的轨迹，计算双方的可达域，在此基础上设计脉冲策略。该方法的赋能过程本质就是基于人的知识进行轨道设计，能够显式给出双方运行轨迹表达式，逻辑清晰，可解释性较强。但是目前研究中脉冲次数一般较少，对于多脉冲变轨，决策空间过大，难以准确预测对方未来的可达域，轨道设计难度大［3，7-9］。同时，该方法的训练效率和赋能效果依赖于人的知识储备和经验，当博弈任务变化后需要重新进行赋能算法设计，因此具有一定的局限性。

2）赋能方法是在第一种方法的基础上，将追逃博弈问题转化为双边最优规划问题，然后基于微分对策理论设计轨道机动策略，其本质是人通过将现有的知识输入给航天器，使航天器具备最优轨迹解算的能力。采用微分对策的目的是求解博弈双方的鞍点（博弈均衡态），在鞍点处，追踪星和逃逸星以各自的最优策略机动，最大化各自的指标函数。采用该方法赋能的航天器可应对双方意图明确、动力学参数已知情况下的追逃问题。但是，对于实际的追逃任务，对方的准确意图及参数难以获取，且对方可采取欺骗、伪装等行为迷惑对手，其自身的指标函数难以获取，因此基于微分对策设计的赋能方法难以应对强博弈态势下的追逃任务［10］。此外，目前关于微分对策轨道追逃博弈的研究主要集中于连续推力航天器［11-13］，对于脉冲推力，由于连续系统+离散控制的最优理论不完备，因此研究成果较少［14-16］。

3）赋能方法基于利用深度学习和强化学习技术。其中深度学习依靠大量样本数据训练神经网络，建立当前状态和机动策略的映射关系。但是其面临样本数据难以获取的问题，需要人为设计双方的机动策略并收集轨迹数据，其本质上是将多种逻辑规则融合为一套决策网络，决策能力取决于训练样本和实际情况的匹配程度［17］。强化学习从统计学的角度出发，将人的决策思维和计算机的算力融合，构建人工神经网络作为决策载体，通过多回合训练，航天器与环境不断交互，收集数据和奖励，实时调整策略，最终具有一定的学习和决策能力，能够在未知环境中应对未知任务［18］。该赋能方法不依赖于人的经验和轨道设计水平，且无需知道精确的动力学模型、环境参数等先验信息，更符合人类的学习过程，在尝试中形成记忆和经验［19］，与上述2种方法相比适应性更强，因此强化学习近年来在航天领取获得广泛关注，取得大量研究成果［20-23］。但是，基于强化学习的训练面临可解释性差、理论证明难、可靠性不高等问题，训练好的决策模型缺乏解析表达式，仅能通过仿真打靶验证其决策的正确性，且缺乏高效的训练赋能方法，航天器通常需要博弈上万回合才能学习到最优追逃策略。

针对航天器追逃博弈训练赋能问题，充分考虑现有方法的不足，将上述3种赋能方法相融合，提出多阶段、逐层递进的训练赋能方法。采用强化学习技术，对追踪星和逃逸星的神经网络进行预训练，预训练分为2步：第1步使追踪星采用强化学习中的邻近策略优化（Proximal Policy Optimization，PPO）算法［24］，逃逸星采用基于逻辑规则的策略，开展训练，直至追踪星神经网络收敛；第2步，使逃逸星采用PPO算法而追踪星采用逻辑规则开展博弈，直至逃逸星网络收敛。然后，在预训练的基础上开展二次训练，使两星同时采用PPO算法，左右互搏，协同进化，最终提升各自的追逃能力。其中，基于逻辑规则的策略充分利用了轨道动力学等先验知识，因此提出的训练方法相当于先利用人的经验知识对航天器一次赋能，再基于强化学习进行二次赋能。

1　问题描述

追踪星需要通过轨道机动抵近到逃逸星的 锥形安全接近走廊（捕获区），而逃逸星旨在通过轨道机动规避追踪星，使追踪星在规定时间内无法进入该区域。同时，逃逸星为了维持原有通信、遥感等业务，其姿态和轨道变化需要满足一定约束。如图1所示，捕获区为图中的锥形区域，该区域与逃逸星位置相关，且在整个博弈过程始终保持对地指向。

采用CW方程描述两者的相对轨道运动：

对于式（1）的线性系统，状态方程可显式求解，得到状态随时间的变化方程：

对于脉冲推力发动机，在进行轨道递推时，可认为速度增量是瞬间产生的，因此式（2）可写为

2　基于逻辑规则的轨道机动策略训练集构建

本章将基于逻辑规则分别设计追逃星和逃逸星的追逃策略，使其作为两星追逃的初级策略，建立策略集，用于训练算法。

2.1　追踪星抵近策略

在CW方程描述的相对轨道运动学框架下，采用基于轨迹预测的方法，通过设计每步的速度增量，实现追踪星在f时刻抵近目标的期望位置。追踪策略流程如图2所示。其中，将安全接近走廊中心线上的点作为f时刻追踪星的期望位置，如图3所示。

2.2　逃逸星轨道机动策略

逃逸星需要在一定的范围内（如图4中的阴影区域所示）运动，为躲避追踪星的抵近，设计了一种基于轨迹预测的逃逸方式，旨在实现在约束包络内，以较少燃料完成逃逸。算法流程如图5所示。

3　多阶段追逃博弈训练赋能算法设计

为了应对对方决策周期、最大推力、机动频率等未知情况下的追逃博弈场景，在基于逻辑规则设计的追逃策略集基础上，提出一种基于强化学习的训练赋能方法，采用多轮训练模式，由简单到复杂，使追踪星和逃逸星逐步、高效地提升博弈能力。

3.1　赋能流程设计

首先追踪星采用强化学习中的PPO算法生成追踪策略，而逃逸星采用2.2节设计的策略进行规避，经过多回合博弈，追踪星的决策网络得到一组最优的权值；其次，令逃逸星采用PPO算法，而追踪星采用2.1节的策略，经多轮博弈后，逃逸星得到最优网络权值，如图6所示。

上述过程分别针对追踪星和逃逸星进行了预训练，其博弈对手的能力相对较弱，网络权值较容易收敛。在此基础上，两星都采用PPO算法进行决策，加载上述得到的网络权值，继承已习得的知识和策略，并在此基础上进行博弈，协同进化，提升各自的追击或逃逸能力。

3.2　PPO算法设计

训练过程采用了PPO算法，PPO是2017年由John Schulman提出的一种基于直接策略搜索的强化学习算法，由于其学习架构清晰、应用简单、适应性强，在围棋博弈、运动体控制、游戏对战等众多领域得到广泛应用，且表现出优异的性能。PPO算法包含训练架构设计、数据采集和网络训练。

首先，根据任务使命设计合理的奖励函数，建立任务和奖励的映射关系，引导航天器朝向奖励最大化的方向学习。

追踪星奖励函数设计如下：

逃逸星奖励函数设计如下：

在此基础上，设计神经网络的结构，确定网络的层数、激活函数类型、连接方式等信息，并设计网络权值更新方法。在数据采集阶段，航天器利用网络模型进行决策，产生轨道机动指令，驱动航天器轨道运动，存储相应的速度、位置、奖励等数据。然后，利用这些数据对动作网络和价值网络训练。其中，动作网络输出各个动作（推力）的概率，价值网络输出各状态的价值函数。在训练过程中，先计算价值网络和动作网络的残差，基于梯度下降法更新网络权值，利用新的网络再进行数据采集，以此循环，直至网络权值收敛。PPO算法的流程如图7所示。

PPO算法的核心在于动作网络的残差（优化指标）计算，其综合考虑了网络前后两次更新的差异度，并对该差异进行限制，提升学习的稳定性。PPO算法的优化指标为

在文献［24］提出的PPO算法架构基础上，着重设计了航天器与环境交互的数据结构和动作空间分布，以及利用PPO算法进行赋能的多阶段训练方法。对于航天器轨道博弈问题，PPO算法中的交叉熵系数2应比价值函数误差项系数1小1～2个量级，航天器轨道博弈状态维数多、时间跨度广、动作空间大，航天器的决策网络难以训练，若交叉熵过大，虽然能够鼓励航天器探索最优解，但是会进一步降低网络收敛速度，甚至无法收敛。相反，对于规模较小的博弈问题，交叉熵可以有效避免算法陷入局部最优解。

4　仿真分析

本章将针对追逃博弈问题，采用如图6所示的赋能流程，基于Python搭建训练环境，完成对追踪星和逃逸星的训练，并分阶段展示神经网络的训练过程。仿真参数见表1。

表1　追逃任务输赢条件相关参数

4.1　追踪星预训练

追踪星采用PPO算法，逃逸星采用2.2节基于逻辑规则的逃逸策略（Rules-based Escape Policy，REP）进行追逃博弈。在两星博弈过程中，追踪星的策略网络及动作网络权值自适应调整，逐渐增加自身的收益，如图8（a）所示。训练3 000回合后，收益收敛到最大值，追踪星在终端时刻抵近到逃逸星的捕获区，相对距离小于50 km（如图8（b）所示），相对角度小于30°（如图8（c）所示）。

4.2　逃逸星预训练

在训练过程中，逃逸星采用PPO算法，追踪星采用2.1节设计的基于逻辑规则的追踪策略（Rules-based Pursuit Policy，RPP）。逃逸星的决策网络逐渐更新，自身收益随着训练局数而不断增加，如图9（a）所示。逃逸星在训练700回合后，可成功躲避追踪星，终端时刻逃逸星与追踪星的相对距离和角度在捕获区之外，如图9（b）和图9（c）所示。

4.3　追踪星和逃逸星的二次训练

在上述训练的基础上，追踪星和逃逸星分别能够应对逻辑规则驱动下的对手，各自决策网络收敛到最优权值。在此基础上开展二次训练，以预训练得到的网络权值为各自决策网络的初始值，采用PPO算法训练，训练结果如图10所示。

由于两星都具备智能博弈能力，且都经过前期的训练，因此两星展现出激烈的博弈态势，双方的收益起伏不定。追踪星无法抵近到逃逸星的捕获区。需要说明的是，由于两星博弈过程中，都是采用PPO算法，且机动能力相同，奖励函数设计相对公平，所以追踪星难以取胜。但是在训练过程中，追踪星和逃逸星的博弈能力都得到提升。

4.4　打靶验证

两星二次训练之后，进行1 000局打靶验证，选择其中一局进行展示，如图11所示。从图11（a）可知，追踪星最终成功抵近到逃逸星的安全接近区内，两星终端相对距离小于50 km，相对角度小于30°。虽然在博弈过程中，两星的燃料都耗尽，但是由于在训练过程中两星也会遇到燃料耗尽的工况，且一方耗尽燃料则意味着失去博弈能力，因此两星会尽可能耗尽对方燃料，从而最大化取胜概率。

为了说明二次训练后的追踪星和逃逸星博弈能力提升，使两星采用不同的机动策略，进行1 000局打靶验证，追踪星的追击成功率见表2。若追踪星采用二次训练得到的决策网络，而逃逸星采用REP，则追踪星的获胜率高达98.2%；反之，若逃逸星采用二次训练得到的决策网络，而追踪星采用RPP，则追踪星的获胜率仅有19.6%。从而说明采用二次训练可有效提升航天器的追逃博弈能力。

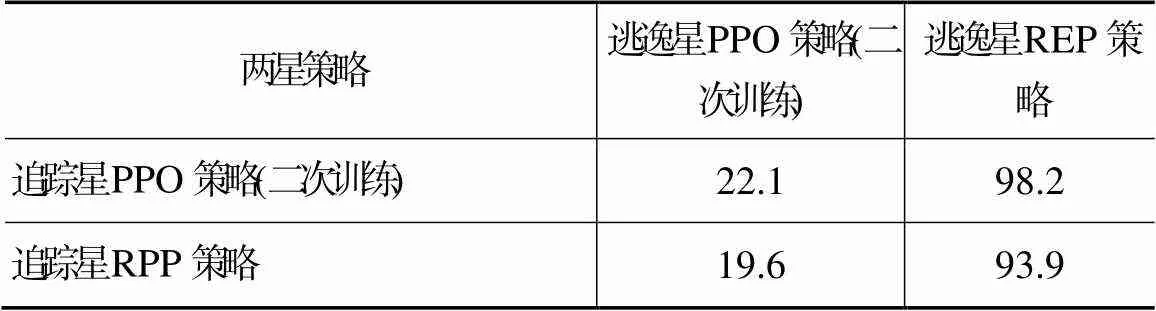
表2　不同追逃策略下追踪星的追踪成功率

5　结束语

针对航天器在轨追逃博弈问题，提出了一种多模复合分阶段学习赋能方法。充分利用轨道动力学信息，递推对方的轨位，并分别针对追踪星和逃逸星设计了基于逻辑规则的博弈策略，以此作为两星的初级决策模式。该策略具有解析表达式，逻辑清晰、形式简单，具有较强的可解释性和通用性。在此基础上提出了一种高效的训练赋能方法，基于强化学习中的PPO方法，采用预训练与二次训练相结合的方式，有效提升了航天器的训练效率和博弈能力。通过仿真分析，验证了本文提出的训练算法的有效性，经过二次训练的航天器能够应对多种策略驱动下的对手，提升了博弈适应性。

［1］ 宫经刚，宁宇，吕楠.美国高轨天基态势感知技术发展与启示［J］.空间控制技术与应用，2021，47（1）：1-7.

［2］ 袁利.面向不确定环境的航天器智能自主控制技术［J］.宇航学报，2021，42（7）：839-849.

［3］ OYLER D W， KABAMBA P T， GIRARD A R. Pursuit⁃evasion games in the presence of obstacles［J］. Automatica， 2016， 65： 1-11.

［4］ PERELMAN A， SHIMA T， RUSNAK I. Cooperative differential games strategies for active aircraft protection from a homing missile［J］. Journal of Guidance， Control， and Dynamics， 2011， 34（3）： 761-773.

［5］ 祁圣君.美军低成本可消耗无人机技术发展综述［J］.飞航导弹，2021（11）：6-11.

［6］ 孙智孝，杨晟琦，朴海音，等.未来智能空战发展综述［J］.航空学报，2021，42（8）：35-49.

［7］ PANG B， WEN C. Reachable set of spacecraft with finite thrust based on grid method［J］. IEEE Transactions on Aerospace and Electronic Systems， 2021， 2021： 3138373.

［8］ LI W. A dynamics perspective of pursuit-evasion： capturing and escaping when the pursuer runs faster than the agile evader［J］. IEEE Transactions on Automatic Control， 2016， 62（1）： 451-457.

［9］ YAN R， SHI Z， ZHONG Y. Guarding a subspace in high-dimensional space with two defenders and one attacker［J］. IEEE Transactions on Cybernetics， 2022 ，52（5）：3998-4011.

［10］ YE D， TANG X， SUN Z， et al. Multiple model adaptive intercept strategy of spacecraft for an incomplete-information game［J］. Acta Astronautica， 2021， 180： 340-349.

［11］ SHEN H X， CASALINO L. Revisit of the three-dimensional orbital pursuit-evasion game［J］. Journal of Guidance， Control， and Dynamics， 2018， 41（8）： 1823-1831.

［12］ LI Z， ZHU H， YANG Z， et al. A dimension-reduction solution of free-time differential games for spacecraft pursuit-evasion［J］. Acta Astronautica， 2019， 163： 201-210.

［13］ TANG X， YE D， HUANG L， et al. Pursuit-evasion game switching strategies for spacecraft with incomplete-information［J］. Aerospace Science and Technology， 2021， 119： 107-112.

［14］ YANG B， LIU P， FENG J， et al. Two-stage pursuit strategy for incomplete-information impulsive space pursuit-evasion mission using reinforcement learning［J］. Aerospace， 2021， 8（10）： 299.

［15］ VENIGALLA C， SCHEERES D J. Delta-V-based analysis of spacecraft pursuit-evasion games［J］. Journal of Guidance， Control， and Dynamics， 2021， 44（11）： 1961-1971.

［16］ 于大腾.空间飞行器安全防护规避机动方法研究［D］.长沙：国防科技大学，2017.

［17］ CHENG L， WANG Z， JIANG F， et al. Real-time optimal control for spacecraft orbit transfer via multiscale deep neural networks［J］. IEEE Transactions on Aerospace and Electronic Systems， 2018， 55（5）： 2436-2450.

［18］ WANG X， SHI P， SCHWARTZ H， et al. An algorithm of pretrained fuzzy actor-critic learning applying in fixed-time space differential game［J］. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2021， 235（14）： 2095-2112.

［19］ WANG Y， DONG L， SUN C. Cooperative control for multi-player pursuit-evasion games with reinforcement learning［J］. Neurocomputing， 2020， 412： 101-114.

［20］ GAUDET B， LINARES R， FURFARO R. Adaptive guidance and integrated navigation with reinforcement meta-learning［J］. Acta Astronautica， 2020， 169： 180-190.

［21］ GAUDET B， LINARES R， FURFARO R. Deep reinforcement learning for six degree-of-freedom planetary landing［J］. Advances in Space Research， 2020， 65（7）： 1723-1741.

［22］ HOVELL K， ULRICH S. Deep reinforcement learning for spacecraft proximity operations guidance［J］. Journal of Spacecraft and Rockets， 2021， 58（2）： 254-264.

［23］ ZAVOLI A， FEDERICI L. Reinforcement learning for robust trajectory design of interplanetary missions［J］. Journal of Guidance， Control， and Dynamics， 2021， 44（8）： 1440-1453.

［24］ SCHULMAN J， WOLSKI F， DHARIWAL P， et al. Proximal policy optimization algorithms［EB/OL］. （2017-07-20）［2022-04-01］. https：//arxiv.org/pdf/1707.06347.pdf.

Multi-stage Reinforcement Learning Method for Orbital Pursuit-Evasion Game of Spacecrafts

YUANLi1，2， GENGYuanzhuo1，2， TANGLiang1，2， HUANGHuang1，2

（1.Beijing Institute of Control Engineering， Beijing 100094， China； 2.Science and Technology on Space Intelligent Control Laboratory， Beijing 100094， China）

An enabled training method based on multi-phase reinforcement learning is proposed to solve the problem of orbital pursuit-evasion of two spacecrafts， so that the pursuer reaches a specific region adjacent to the evader at the terminal moment while the evader attempts to avoid being chased by means of orbital maneuvering. First， a training set of the pursuer and chaser is constructed. The two rules-based pursuing and evasion policies are proposed for the pursuer and evader， respectively， in which the expected position and pulse policy are analytically designed based on the prediction of the terminal position of the other spacecraft. Second， a multi-mode training method based on reinforcement learning is proposed to enhance the training efficiency and the ability to confront with uncertain adversaries. Third， the spacecraft is pre-trained by confronting with the other spacecraft endowed with the rules-based policies. Based on the pre-trained network， the network is re-trained in which both the spacecrafts are driven by the proximal policy optimization （PPO） scheme where the network weights are updated gradually. Finally， simulations are conducted to evaluate the effectiveness of the proposed training approach. The results show that the spacecraft with re-trained network could enhance the success rates of pursuit and escape.

orbital pursuit-evasion； game decision making； reinforcement learning； enabled training； multi-stage learning

2022‑04‑26；

2022‑06‑14

袁利（1974—），男，博士，研究员，主要研究方向为航天器建模与仿真、智能控制、高精度控制和鲁棒容错控制技术。

TN 911.73； TP 391.9

A

10.19328/j.cnki.2096⁃8655.2022.04.003