苏南区块声波测井计算孔隙度方法改进
2022-12-16王亚兰杨超超任小锋蔡芳王园谢文汇赵敏
王亚兰,杨超超,任小锋,蔡芳,王园,谢文汇,赵敏
(1.中国石油集团测井有限公司长庆分公司,陕西西安 710200;2.中国石油集团测井有限公司地质研究院,陕西西安 710076;3.中国石油长庆油田分公司第一采气厂,陕西西安 710021)
孔隙度是反映储层地质特征的一个重要参数,准确计算孔隙度也是准确计算含水饱和度、渗透率等其他储层参数的前提。多年来苏里格气田上古生界测井解释都是应用常规的单声波时差计算储层孔隙度[1-5]。苏南区块位于苏里格气田中区南部,属于典型的低孔、低渗砂岩储层。储层物性较差,岩性对孔隙度的影响大,储层非均质性强,地层骨架值变化较大,很难用定值来表示,声波测井用传统的威里公式计算孔隙度方法难以准确求得地层真实孔隙度。
为此,本文提出了从声波测井计算孔隙度的影响因素考虑,结合岩心分析数据计算低孔低渗储层孔隙度的方法[6-8],然后根据泥质含量的不同,在岩心回归公式的基础上对泥质较重的层段进行了泥质校正,消除了由于泥质含量的影响导致的孔隙度计算误差,从而计算出地层的真实孔隙度。
1 常规声波测井计算孔隙度方法及影响因素
1.1 计算方法
声波时差测井是记录声波在地层中传播1 m 所需要的时间。它与岩石骨架成分、孔隙度的分布和孔隙中流体的性质有关。对于压实和胶结良好的纯砂岩孔隙度用下面的威里时间平均公式计算:
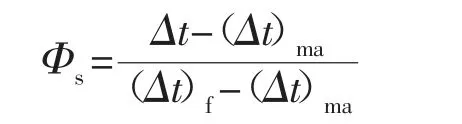
式中:Φs-声波孔隙度,%;Δt-地层声波时差测井值,μs/m;(Δt)ma-地层骨架声波时差,μs/m;(Δt)f-地层中流体声波时差,μs/m。
对于含泥质岩石声波测井计算孔隙度公式为:

式中:Φs-声波孔隙度,%;Δt-地层声波时差测井值,μs/m;(Δt)ma-地层骨架声波时差,μs/m;(Δt)f-地层中流体声波时差,μs/m;(Δt)sh-纯泥岩声波时差,μs/m;Vsh-泥质含量,%。
1.2 影响因素
对于砂泥岩地层,如果是纯砂岩、纯水层、地层压实程度较高的情况下,声波时差测井利用威里公式即可得到较精确的孔隙度计算结果。但对于含有天然气或轻质油的地层,且地层疏松压实程度不高的情况下,威里公式中涉及到的岩石骨架、泥质以及流体等参数随不同地区岩石成分、泥质性质和流体的不同而改变,用常规的计算方法就很难反映真实的地层孔隙度。
2 声波测井计算孔隙度方法改进
2.1 岩心分析数据结合声波时差计算孔隙度
本文提出利用本区岩心分析孔隙度与声波时差进行相关性分析并得到相应的孔隙度回归公式,见图1。

图1 岩心分析孔隙度与声波时差相关性分析
可得到声波孔隙度回归公式为:

相关系数为0.82。
这种岩心回归公式方法,当地层岩性比较纯的时候,和取心采样数据比较接近,计算的孔隙度结果与实际情况比较符合。但如果地层泥质含量较高(Vsh≥0.35%)时,由于泥质疏松的特性会增加声波在地层中的传播时间,导致声波时差增大,从而使声波计算的孔隙度结果比实际地层孔隙度偏大,与实际地层情况不符。在这种情况下,要想得到更为准确的孔隙度,就需要做泥质校正。
2.2 泥质校正及参数选取
在泥质校正方面,参考借用威里公式中关于泥质校正部分的方法,即:

由于本区没有相关的泥质和流体参数等实验室数据,只能利用测井数据进行估算并验证。
2.2.1 岩石骨架声波时差和泥质声波时差的选取 砂岩骨架声波时差的理论值为182 μs/m,该值是在纯石英情况下试验得到的声波时差值,但本区地层岩石成分比较复杂,不仅为石英,所以不能用理论值进行孔隙度的计算。对此,为了得到适合本区的岩石骨架参数,首先利用本区的所有井对目的层段(盒7~山2)作声波时差与泥质含量交会图,见图2。
图2 中横坐标为泥质含量(VCL,%)、纵坐标为声波时差(DT,μs/m)。为了统计数据的真实性,把由于井眼垮塌导致的声波时差异常值进行了剔除。从图中可以看出有两个明显不同的趋势,其一是在泥质含量大于0.4%的右边区域中,声波时差数值随着泥质含量的增加而增大,符合正常趋势;而在泥质含量小于0.4%的左边区域中,声波时差随着泥质含量的增加而减小,与正常应有的趋势不一样。经过分析认为之所以产生左边的异常趋势,是因为目的层段岩性较好的砂岩中都含有天然气,而天然气的存在会导致声波时差的异常增大,且岩性物性越好的储层,这种异常会更加明显。
为了证实本文的观点,对本区上部不含气的非目的层段(盒4~盒6)作了同样的交会图,见图3。
从图3 可以看出在没有天然气的情况下,数据点趋势就变得单一了,与图2 右边趋势相近,只是由于压实程度的不同,数据点整体稍微向下移动(即声波时差增大的方向),和本文的分析一致。

图2 目的层段声波时差与泥质含量交会图
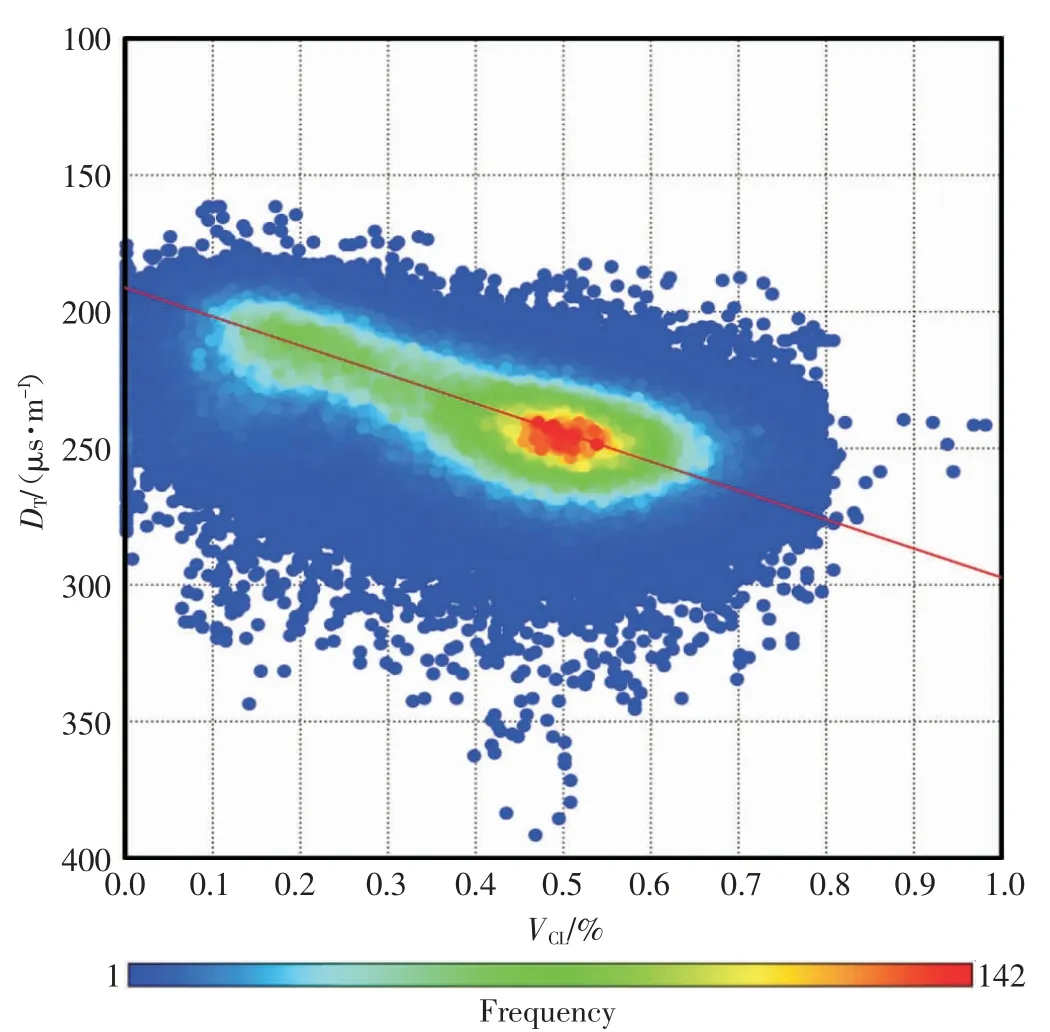
图3 非目的层段声波时差与泥质含量交会图
所以就可以确定本区目的层段岩石骨架(VCL=0)的声波时差为178 μs/m,纯泥岩(VCL=1%)的声波时差为257 μs/m。
2.2.2 流体声波时差的选取 由于本区目的层段的流体多为水和气的混合流体,所以也不能采用水的声波时差理论值(620 μs/m)计算孔隙度。可以尝试从测井数据中估算该参数。根据前面描述,声波计算孔隙度公式为:

将公式进行转换变形可得到:
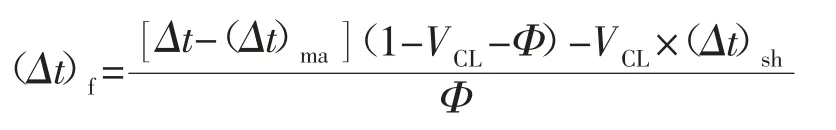
于是,利用该公式以及以前中子、密度交会计算的孔隙度对本区所有井计算出流体声波曲线并作该曲线频率分布统计图,见图4。

图4 流体声波曲线频率分布统计图
在作图时,增加了泥质含量小于0.25%的限制条件,因此该图只反映砂岩段流体声波曲线的分布特征。最终统计出分布频率最大的声波时差值632 μs/m 作为本区流体声波时差值。这样,泥质校正所需要的所有相关参数都已经得到:
(Δt)ma(地层骨架声波时差):178 μs/m
(Δt)f(地层中流体声波时差):632 μs/m
(Δt)sh(泥岩声波时差):257 μs/m
代入到公式中:

得到校正量为:
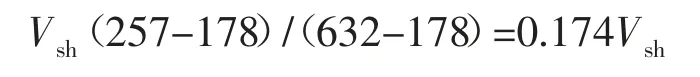
考虑到只有在泥质含量较重的地方,利用声波计算的孔隙度会偏大,参考前面目的层段泥质含量和声波时差交会图中的趋势拐点以及地质分析中计算砂岩的截止值,于是在地层泥质含量较高(Vsh≥0.35%)时,声波测井计算孔隙度的回归公式就改进为:
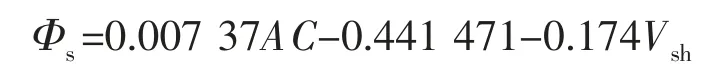
而在泥质含量较低(Vsh<0.35%)时,用原声波孔隙度回归公式,即:

3 应用效果评价
为了对改进的声波孔隙度计算方法进行验证,利用声波时差数据对四口取心井重新计算了孔隙度(PHI_NEW),并与未做过泥质校正的孔隙度曲线(PHI)以及岩心分析孔隙度进行了对比,对比结果见图5、图6。

图5 泥质校正后声波孔隙度与岩心分析孔隙度对比

图6 未做泥质校正声波孔隙度与岩心分析孔隙度对比
二者分别与岩心分析孔隙度对比后可以看出,做过泥质校正后的孔隙度相比校正前与岩心孔隙度的相关系数明显提高,由0.72 提高到了0.82。
4 结论
(1)储层物性较差,非均质性强时,地层骨架值变化较大,很难用定值来表示,声波测井用传统的威里公式计算孔隙度方法难以准确求得地层真实孔隙度。
(2)本文提出岩心分析数据结合声波时差进行相关性分析,得到相应的孔隙度回归公式。当地层岩性比较纯的时候,直接用回归公式计算孔隙度;当地层泥质含量较高时,在孔隙度回归公式的基础上进行了泥质校正,消除了由于泥质含量的影响导致的孔隙度计算误差,得到更为准确的孔隙度。
(3)通过将本次研究提出的声波测井计算孔隙度改进方法和岩心孔隙度进行对比,证实本方法计算的孔隙度与岩心分析结果吻合较好,和常规的声波测井计算孔隙度方法相比,更加接近岩心数据,可以准确地反映地层真实孔隙度。
