新型五螺箍矩形短柱轴压承载力计算分析

2022-12-16刘成清邓佑毅方登甲

西南交通大学学报 2022年6期

刘成清，邓佑毅，方登甲，刘悦

（西南交通大学土木工程学院，四川成都 610031）

五螺箍是一种新型组合式螺旋箍筋，其构造方式为中间一个大螺箍，四角为四个小螺箍.相比传统的单螺箍圆形柱，四个小螺箍可以约束四个角落的混凝土，使得螺旋箍筋可以适用于矩形截面.五螺箍为机械自动化生产，相对于传统箍筋有更高的效率[1].目前，五螺箍的应用与研究主要在中国台湾，且设计与研究参照了文献[2].

国内外学者对单螺箍约束混凝土开展了大量的理论与试验研究，而多螺箍约束混凝土的研究较少.Mohamed等[3]通过试验对复合箍筋柱进行了参数分析，主要研究了配箍形式和体积配箍率对试件力学性能的影响.Mander等[4]通过对大量约束混凝土柱试件进行轴心受压试验，得到一套约束混凝土的本构模型.Assa等[5-6]对一系列螺旋箍筋柱试件进行实验，得到螺旋箍筋约束混凝土的本构关系.过镇海等[7-8]进行方形箍约束混凝土在反复荷载下的应力-应变全曲线试验研究，试验得出试件强度和延性与体积配箍率呈正相关关系.唐琼等[9]基于多螺箍筋试验数据建立有限元模型，分析受力机理提出轴压承载力计算公式.史庆轩等[10]通过多根不同配箍形式的方形截面柱进行轴压试验，并对其延性与强度进行影响因素分析.翁正强等[11]对多个五螺箍短柱进行了轴压试验，研究了三个不同系列小螺箍直径对柱整体力学性能的影响.郑亮[12]通过试验研究了方钢管混凝土和配螺旋箍筋方钢管混凝土短柱的力学性能，并且对短柱承载力计算方法进行理论研究.傅明月[13]对五螺箍混凝土柱进行了轴心受压与偏心受压试验，发现螺旋箍筋能明显地提高柱的承载能力和延性性能.Liang等[14]进行9根足尺多螺旋箍筋约束方形短柱的试验，发现减小螺旋间距可以明显提高柱的轴压承载力和延性.

由于目前对五螺箍柱轴压承载力计算式的研究鲜有报道，因此，有必要对其力学性能进行进一步研究，以提出适用于五螺箍柱的轴压承载力计算式.本文利用ABAQUS软件，首先，基于试验模型建立有限元模型，并将有限元分析结果与已有的试验结果进行对比分析，以验证有限元模型分析结果的准确性.接着，基于材料用量相等的原则，创建4种不同配箍形式的矩形截面柱，并进行力学性能对比分析.最后，对五螺箍柱轴压承载力进行影响因素分析，提出基于体积配箍率的轴压承载力计算式.

1 有限元分析模型

1.1 混凝土的本构关系

混凝土本构模型采用有限元软件ABAQUS中内置的塑性损伤模型，损伤因子按文献[15]公式计算.因Mander模型[14]对不同箍筋的作用形式有不同的计算式，故本构关系采用Mander模型[14]，模型的具体表达如下：

1.2 采用的钢筋本构

钢筋采用理想弹塑性模型，具体表达形式为

式中：Es、Fy分别为钢筋的弹性模量和屈服强度；εs为钢筋应变；εy为钢筋屈服应变；σs为钢筋应力.

1.3 有限元模型验证

采用位移协调分离式来分析模型.混凝土采用C3D8R单元，钢筋采用T3D2单元.对钢筋和混凝土之间的连接，采用Embedded region进行两者的自由度耦合，不考虑钢筋和混凝土之间的连接滑移.为了使柱体的边界约束条件接近实际受力情况，在柱体上、下两端采用铰接连接方式，并在柱顶进行位移加载.本文选取文献[16]中的试件C2-1、C2-3、C2-4和C2-5，用有限元软件ABAQUS建模进行分析.4根短柱的试验设计参数以及试验和有限元分析结果如表1所示.图1为各试件试验和有限元分析的应力-应变曲线图.

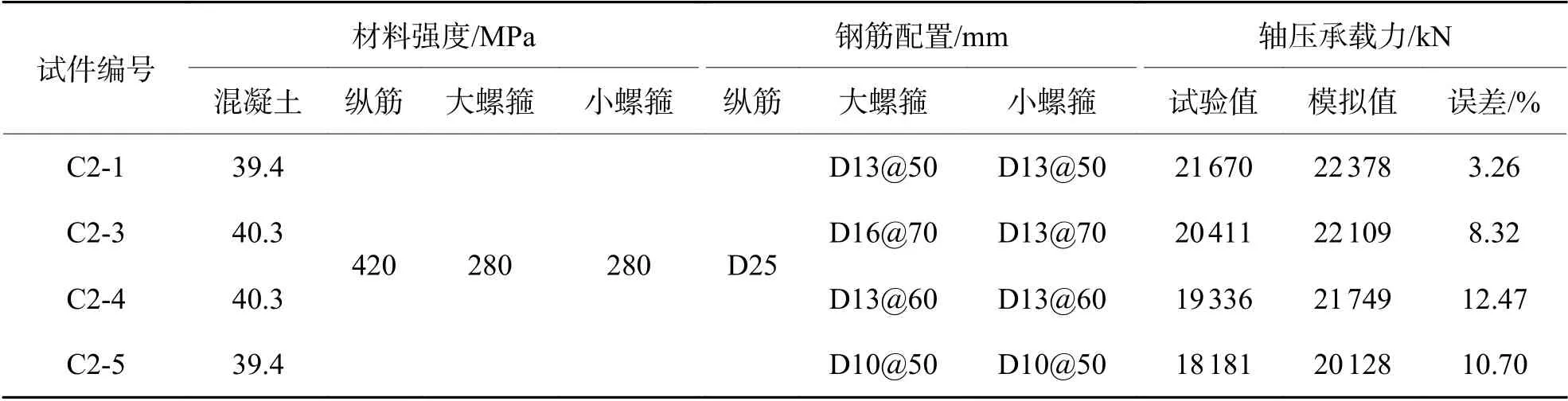
表1 试验和有限元计算结果对比Tab.1 Comparison of experiment and finite element calculation results

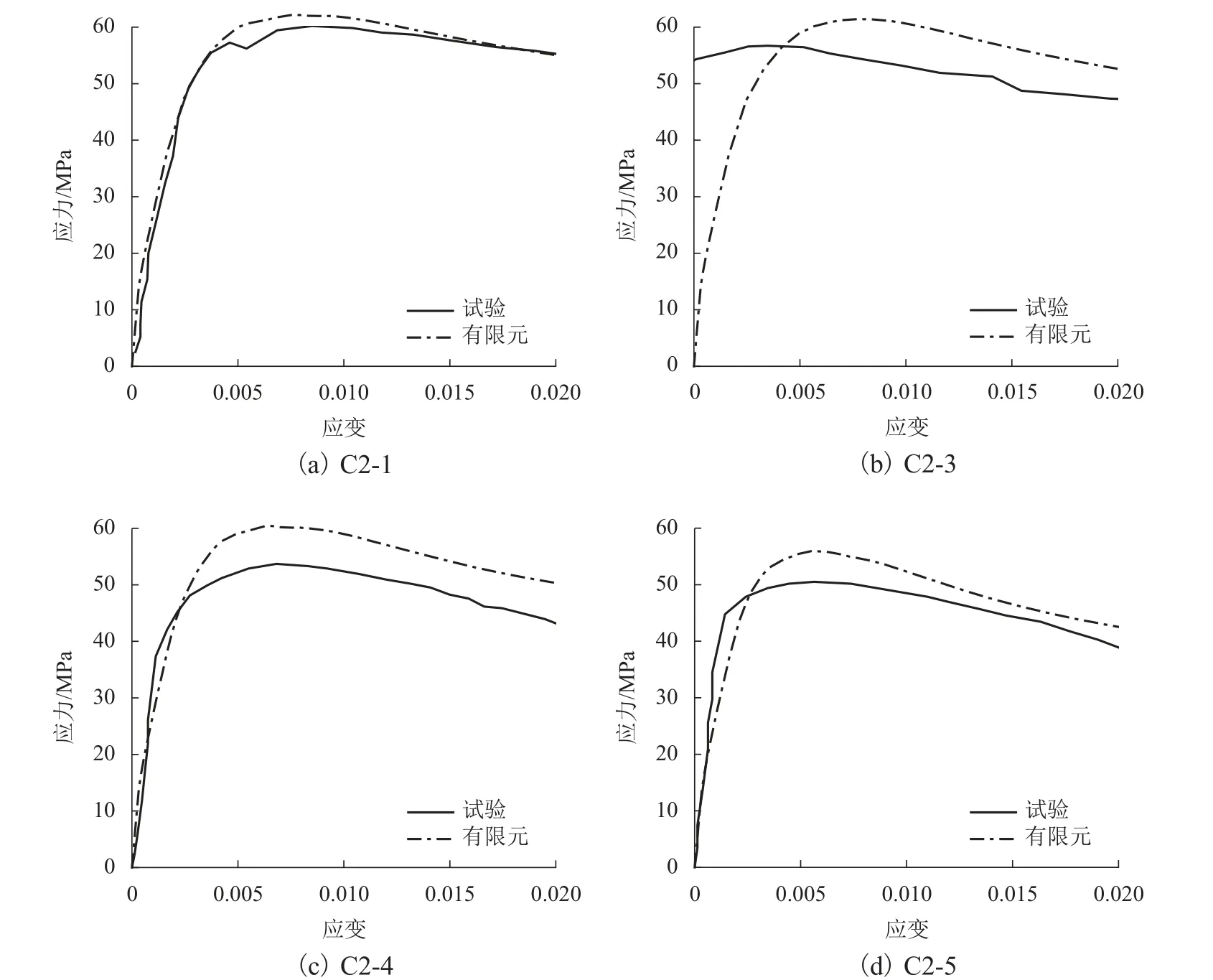
图1 应力-应变曲线Fig.1 Stress-strain curves

从表1可以看出：轴压承载力的模拟结果稍微高于试验结果，轴压承载力最大误差为12.47%，最小误差为3.26%，平均误差仅为8.68%，可以说明有限元模拟得到的轴压承载力与试验结果比较接近.从图1可以看出：有限元模拟结果和试验结果吻合较好.

2 配箍形式对峰值荷载和延性的影响分析

基于材料用量相等的原则，考虑混凝土强度等级和配箍形式对钢筋混凝土柱受压性能的影响，设计了混凝土强度等级从C25 ～ C50的6组钢筋混凝土柱分析模型，每组都包括五螺箍、五环箍、矩形箍、矩形螺旋箍4种配箍形式，各配箍形式模型的几何参数和材料构成如图2所示.为尽可能符合实际情况，柱高取1.5 m，即反弯点处截取一半楼层高度.五螺箍、五环箍、矩形箍、矩形螺旋箍配箍形式的钢筋混凝土柱模型用钢量分别为1.10 × 107、1.09 ×107、 1.10 × 107、1.10 × 107mm3，最大相差为0.5%，可视为材料用量相等.4种配箍形式模型的纵筋配筋率为1.82%，满足轴心受压构件纵筋最小配筋率0.5%、最大配筋率5.0%的要求，箍筋强度均为280 MPa，纵筋强度均为400 MPa.

在焊接温度530 ℃和焊接压力3.5 MPa的条件下，保温时间对铝合金扩散焊接头抗拉强度的影响如图3所示.从图3可知，当保温时间为3 h时，焊接接头的抗拉强度为56.7 MPa.随着保温时间延长，焊接接头的抗拉强度先增加后减小.在保温时间为7 h时，接头抗拉强度达到最大值137.3 MPa.在扩散焊接的过程中，延长保温时间可使界面元素充分地扩散，有利于焊接接头组织与成分的均匀化.保温时间较短时，界面原子间扩散不充分，不能形成广泛的原子间结合，因此接头的剪切强度较低.但保温时间过长会导致晶粒长大，使接头的抗拉强度降低.

图2 4种不同配箍形式矩形截面柱Fig.2 Four types of rectangular columns with different stirrup configurations

有限元分析结果如图3、4所示.从图3中可以看出：五螺箍柱的峰值承载力较其他3种柱都高.为反映短柱的延性性能，采用已有的对延性定义的指标延性系数DI[17]来表示，如式（11）所示.

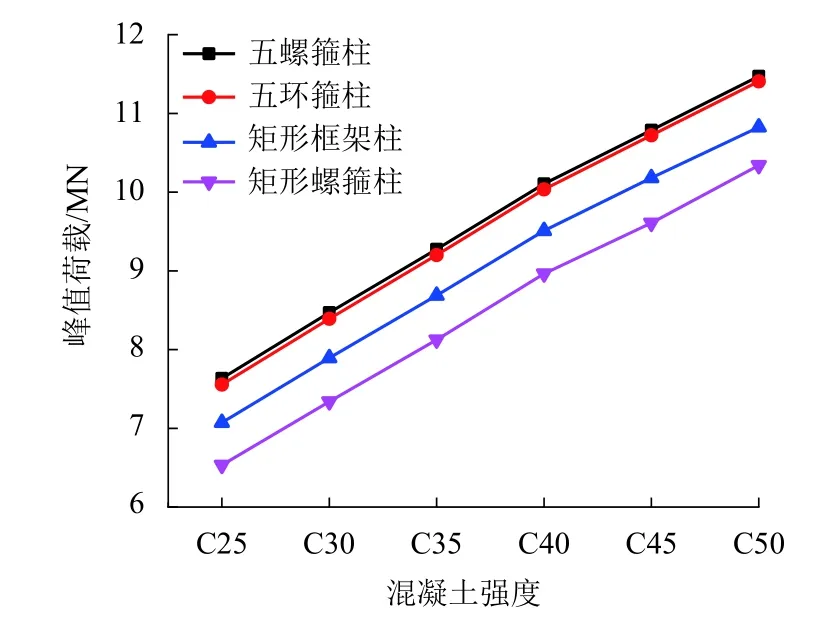
图3 混凝土强度等级-峰值荷载Fig.3 Concrete strength grade-peak load

式中：u11为峰值荷载时的位移；u85为峰值荷载下降到85%时的位移.

从图4可以看出：五螺箍的延性优于其他3种柱，五螺箍较五环箍、矩形箍和矩形螺旋箍柱构件峰值承载力均值分别提高0.78%、6.70%和13.73%，延性系数均值分别提高2.00%、10.32%和10.41%，表明五螺箍柱具有较优的承载力及延性，这与文献[11]中的试验结论相符.

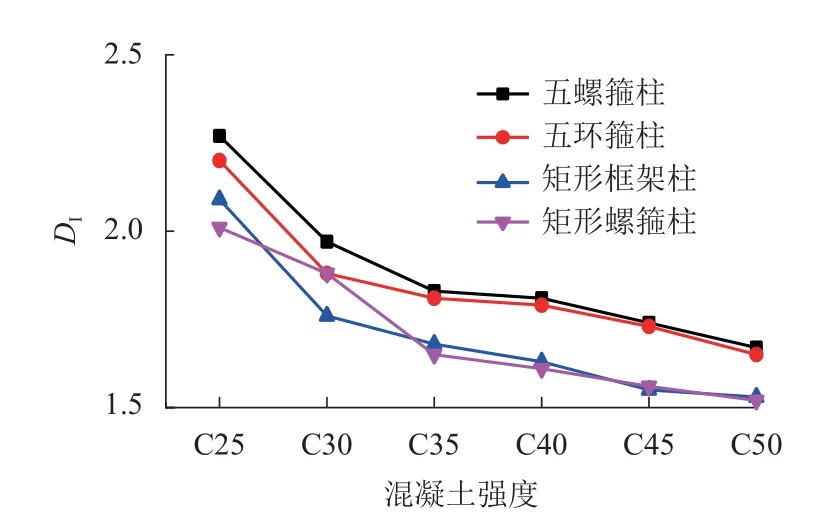
图4 混凝土强度等级-延性系数Fig.4 Concrete strength grade-ductility coefficient

由于五螺箍柱的各性能指标均较优，有必要对五螺箍轴压承载力及延性进行影响因素分析，为提出五螺箍轴压承载力的计算式奠定基础.本文按照《混凝土结构设计规范》（GB 50010—2010）[18]（以下均简称《混规》）的要求，设计了9个螺旋箍筋间距为40 ～ 80 mm （或dcor/5，其中，dcor为核心区混凝土的直径，可按螺旋箍筋内表面直径取值）的模型，其中，体积配箍率的计算式[11]为

式中：D、d分别为大螺箍和小螺箍的直径；Asp1、Asp2分别为大螺箍和小螺箍单根钢筋的截面面积；Ach为五螺箍所约束的混凝土面积；s5为五螺箍的间距.

有限元分析结果如图5和表2所示.图5（a）中模型M-1、M-2、M-3分别对应的箍筋间距为45、50、55 mm，可以看出：随着箍筋间距的减小，五螺箍柱的峰值荷载和延性系数都有提高，曲线下降段也更为平缓，延性更好.图5（b）中模型M-4、M-2、M-5分别对应的混凝土强度为23.4、26.8、29.6 MPa，可以看出：随着混凝土强度的提高，五螺箍柱的峰值荷载有明显的提高，但延性系数减小，延性不能得到改善.图5（c）中模型M-2、M-6、M-7对应的箍筋强度分别为335、400、500 MPa，可以看出：提高螺旋箍筋的强度，五螺箍柱的峰值承载力和延性系数有所提高，主要表现为箍筋的约束应力提高，约束效果更好，下降段曲线也更为平缓，延性得到了较大改善.图5（d）中模型M-2、M-8、M-9对应的大（小）螺箍直径分别为10（6）、10（8）、12（8）mm，可以看出：随螺旋箍筋截面直径的增大，峰值荷载和延性系数随之提升，曲线下降段也更为平缓，五螺箍柱的轴压承载力和延性都有很大改善.对比图5（a）和图5（d），箍筋间距的减小和箍筋直径的增大都是提高体积配箍率的方式，对五螺箍柱的影响结果相似，均能提高构件的峰值承载力和延性，有利于提高构件在考虑近场地震[19]等不利作用下结构构件极限变形能力.故下文将基于体积配箍率研究五螺箍柱的轴压承载力计算式.

表2 有限元模型主要参数Tab.2 Main parameters of finite element models

图5 分析结果荷载-位移曲线Fig.5 Load-displacement curves of analysis results

3 轴压承载力计算

五螺箍柱的轴压承载力主要由以下4部分组成：混凝土抗压承载力、纵筋抗压承载力、大螺箍和小螺箍分别对核心区混凝土的约束效应而产生的承载力.本文主要研究大、小螺箍通过对混凝土约束产生的承载力.不同的配箍形式产生的约束效果不同，相对于矩形箍，圆形箍具有整体变形小，应力分布均匀及有效约束面积大等优点.五螺箍柱中，大螺旋箍筋主要约束了柱中部的混凝土，小螺旋箍筋主要约束了柱四个角落的混凝土，二者相互弥补各自的弱约束区，较好地约束了整个截面.螺旋箍筋有效约束区如图6所示，其中阴影部分表示有效约束区.

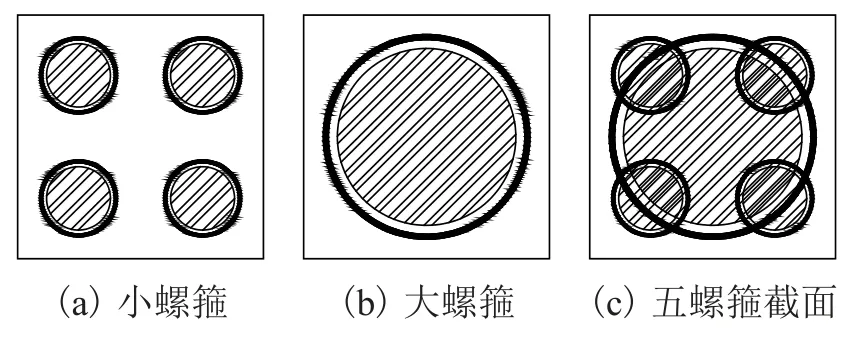
图6 有效约束区Fig.6 Effective restraint zones

由于大、小螺箍的约束部位不同，故计算时应分别计算两者提供的约束作用力.螺旋箍筋的有效约束面积[4]为

式中：s为螺旋箍筋的间距.

《混规》[18]关于约束混凝土的轴心抗压强度为

式中：σr为核心混凝土受到的径向压应力值，如式（15）；fc为混凝土抗压强度设计值；对于约束混凝土，取 β=4.

式中：fy为螺旋箍筋的抗拉屈服强度；Ass为单根螺旋箍筋的截面面积.

在Hobbs[20]的研究中有

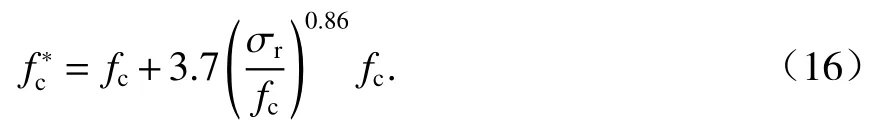
根据叠加理论，基于《混规》[18]的五螺箍轴压承载力为

式中：Ass1和Ass2分别为单根大、小螺旋箍筋的截面面积；fy1和fy2分别为大、小螺旋箍筋的屈服强度；s1与s2分别为大、小螺旋箍筋的间距；dcor1和dcor2分别为大、小螺旋箍筋包围的核心区混凝土直径；Acor为混凝土核心区面积；fy3为纵筋抗压强度；As1为纵筋面积；Ac1、Ac2分别为大、小螺旋箍筋的有效约束面积.

根据叠加理论，基于Hobbs[20]修正后的五螺箍轴压承载力为

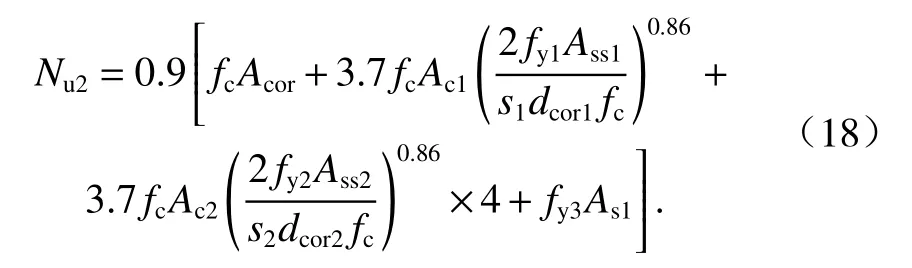
文献[11]提出的五螺箍轴压承载力为

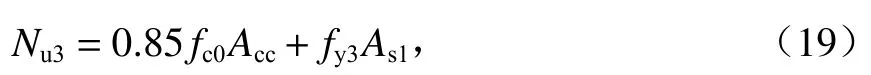
式中：Acc为五螺箍所约束的混凝土面积.

美国ACI规范[2]规定的短柱受压承载力为

式中：Ac为混凝土柱全断面积；方括号外的“0.85”表示结构抗力折减系数，方括号内的“0.85”表示尺寸效应对受压承载力的影响系数.

由上文轴压承载力影响因素分析可知，材料的强度、箍筋的间距、箍筋的面积等都对五螺箍柱的承载力有影响，为简便起见，本文将这些因素统一考虑为体积配箍率 ρv，这样就可以很大程度上减小承载力计算的复杂程度.由于混凝土及纵筋所提供的竖向承载力计算较为明确，无需修正，本文重点修正螺旋箍筋对混凝土的约束作用.将每个构件的轴压承载力减去混凝土和纵筋提供的竖向承载力，得到螺旋箍筋提供的竖向承载力N1，由此可以推出约束作用系数为

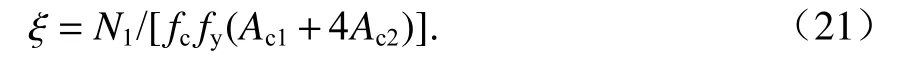
ξ随 ρv的变化关系如图7所示，对两者进行线性关系拟合，结果可以看出两者大致成线性分布.根据 ξ与 ρv的关系，参考《混规》[18]和Hobbs[20]修正按叠加理论计算的公式，本文提出五螺箍柱的轴压承载力为

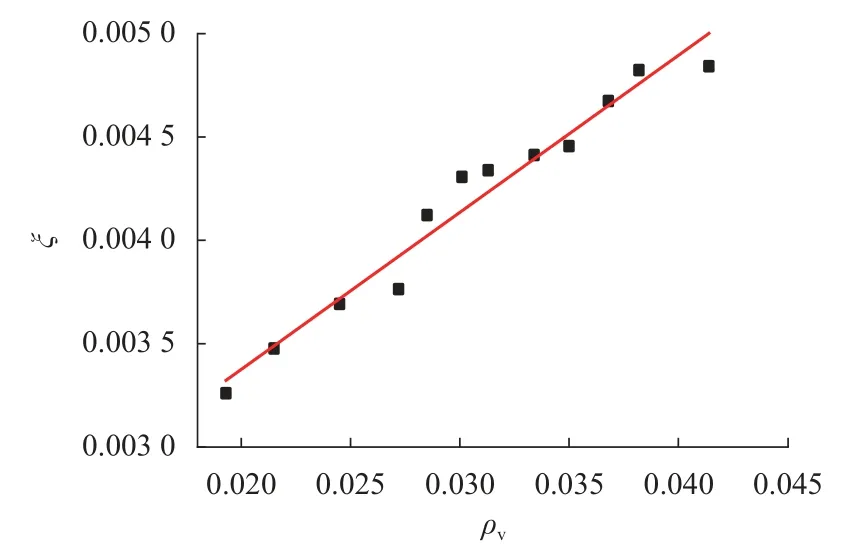
图7 约束作用系数-体积配箍率关系Fig.7 Relationship between confinement coefficients and volume-stirrup ratios

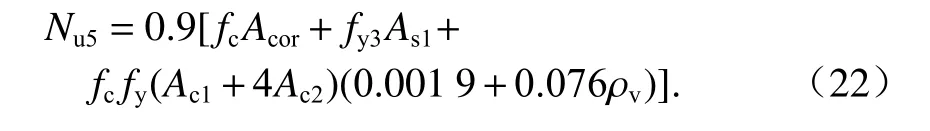
采用上述5个承载力计算式（即式（17）～（20）和式（22）），不考虑安全储备及折减系数，混凝土强度统一采用轴心抗压强度标准值，得到上述9个模型和4个试验[16]构件的轴压承载力，分别如表3和表4所示.表中：δ1、δ2、δ3、δ4和 δ5为5个承载力对应的相对误差.

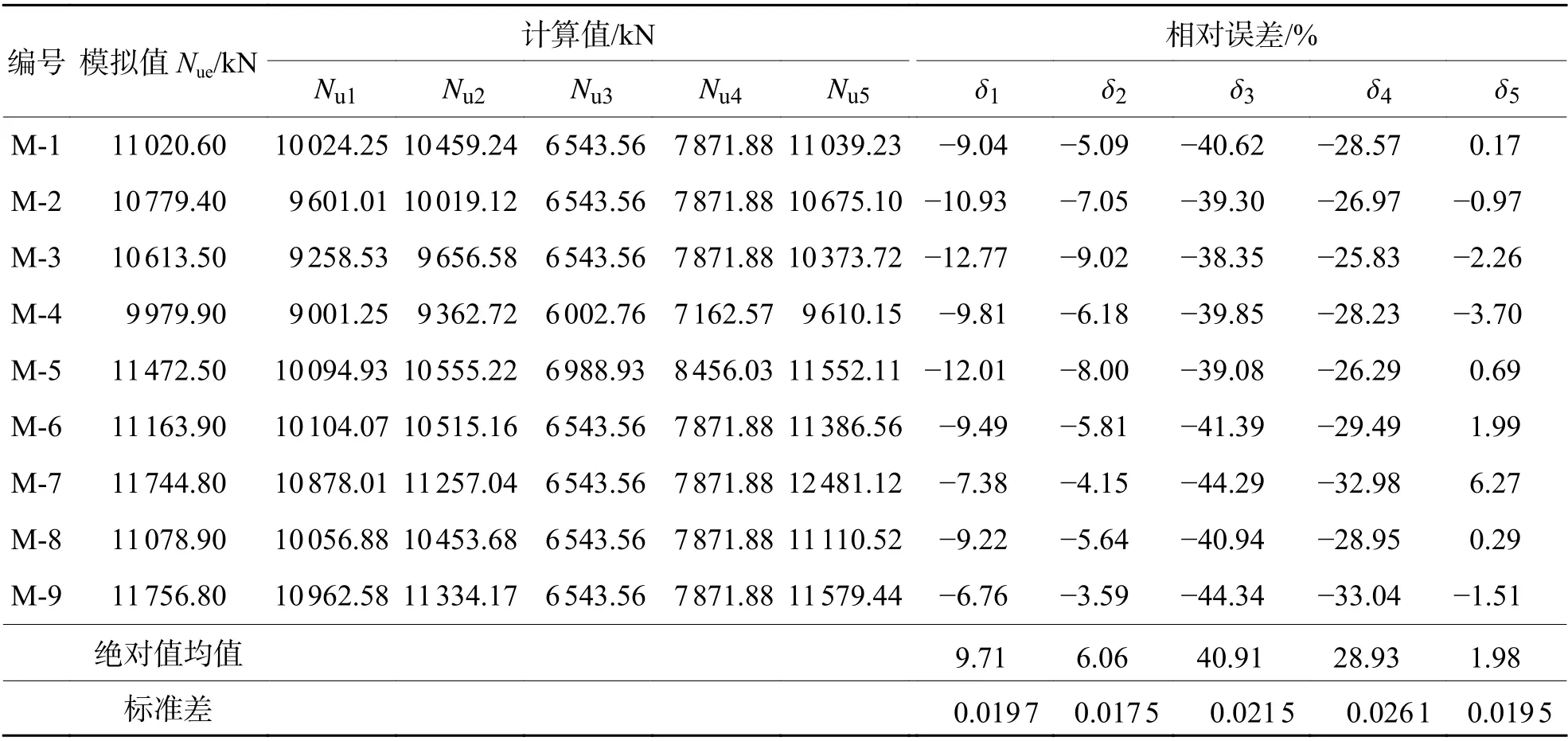
表3 9个模型的轴压承载力计算Tab.3 Axial compression bearing capacity calculation of nine models

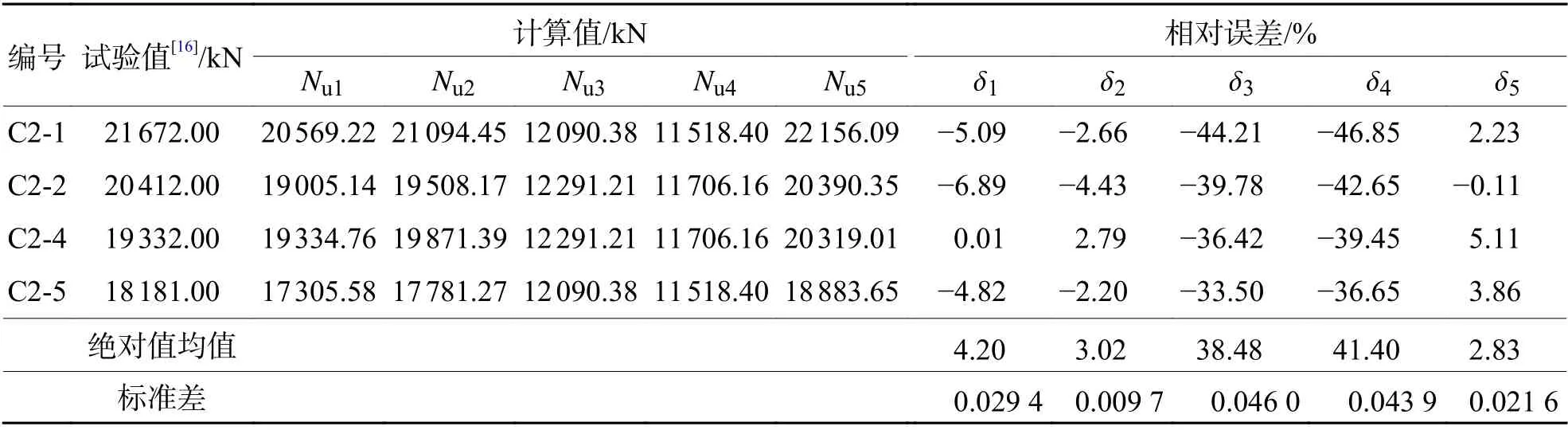
表4 4个试验构件的轴压承载力Tab.4 Axial compression bearing capacity calculation of four test members

由表3数据可知：计算值Nu3远远小于模拟值和试验值，原因是该式中混凝土的计算面积是五螺箍约束混凝土的面积，且混凝土抗压强度取的是轴心抗压强度标准值，而不是约束后的混凝土抗压强度值；计算值Nu4相比模拟值和试验值误差较大，原因是计算式仅考虑了纵筋和混凝土提供的竖向抗压承载力，而忽略了螺旋箍筋对混凝土的约束作用；计算值Nu1和Nu2比较接近模拟值和试验值，两个计算式既考虑了混凝土和纵筋所提供的竖向抗压承载力，又考虑了箍筋对混凝土的约束效应；在分析范围内，本文提出的修正式的计算值Nu5更加接近模拟值和试验值，与模拟值的误差均值为1.98%，与试验值的误差均值为2.83%，且标准差分别为0.0195和0.0216，总体上偏于安全.用体积配箍率考虑箍筋的间距、箍筋的面积、螺箍直径等多因素使得承载力计算更加简便与精确，且具有很好的实用性.