面向碳达峰的电煤运输与采购问题研究

王新月，马晓凤

（1.武汉理工大学 智能交通系统研究中心，湖北 武汉 430063；2.武汉理工大学 国家水运安全工程技术研究中心，湖北 武汉 430063)

0 引言

在第21届联合国气候变化大会上，中国承诺2030年前碳排放达到峰值，2060年前实现碳中和。当前煤炭是我国的主要能源，且由于新能源代替煤炭在短时间内不易实现，因此煤炭在未来一段时间内仍是我国的主要能源[1]。我国的煤炭分布呈现“西多东少，北多南少”的特征，煤炭运输距离远、运量大，减少煤炭运输与燃烧的碳排放对于实现碳达峰具有重要意义。

国内外学者对运输问题与碳排放问题进行了较多研究。运输路径优化方面，Fazayeli等[2]为了确定运输问题最优的路线与节点，构建了以运输费用最小为目标函数的线性规划模型，并设计一种新染色体结构的遗传算法进行求解，结果表明该算法能够合理解决通用代数建模系统(GAMS)在长时间内也无法达到最优解的问题；陈汨梨等[3]针对运输过程中的不确定性因素，开展了不确定条件下的多式联运路径优化研究，采用随机规划理论估计不确定值，并设置最小运输总成本为目标函数，采用K短路算法进行求解。碳达峰方面，庄贵阳等[4]分析了碳达峰的政策内涵与实现路径，探讨碳达峰目标导向下可再生能源的发展前景，指出碳达峰的深层次问题是能源问题，高比例发展非化石能源，以能源脱碳推动经济社会绿色低碳转型；Tang等[5]从区域的视角考察电力行业碳达峰的时间，开发了国家能源技术-电力(NET-Power)模型评估技术发展与能源结构改变对于碳排放的影响。运输行业的碳排放方面，成耀荣等[6]从运输企业的角度出发，建立了考虑碳排放的多任务多式联运路径优化模型，并对不同的运输任务和模式进行分析，设计变长符号编码机制的文化基因算法对模型进行求解。

碳税制度最早由英国学者庇古提出，主要思想是用税收方式弥补社会对环境造成的损害。为解决碳排放带来的负外部性问题，少数发达国家从20世纪90年代开始征收碳税，当前我国的碳排放权交易制度正从试点地区的重点行业走向全国性交易阶段[7]。Anton等[8]构建了多部门静态可计算一般均衡模型，并以俄罗斯为例进行实证分析，结果表明俄罗斯用碳税代替劳动税后，不仅能增加社会福利，还能减少碳排放。

碳达峰背景下，将能源问题与运输问题综合起来考虑经济成本与碳排放成本的研究较少。为此，考虑煤炭的购买、运输、使用3个阶段，引入碳税制度，以火力发电企业盈利最大为目标函数，建立多式联运路径优化-碳排放模型，研究碳税制度下火力发电企业盈利最大的最优采购方案。

1 问题描述与模型建立

1.1 问题描述与假设

假设规划系统内有i个煤炭产地向消费地供煤，同一产地出产n种不同的煤，不同种类煤炭的发热量、价格、燃烧时的碳排放量不同。煤炭从产地到消费地会经过若干转运节点，每2个节点之间可以通过水路或者铁路连接，水路运输和铁路运输的运价与碳排放量不同。煤炭运输示意图如图1所示。

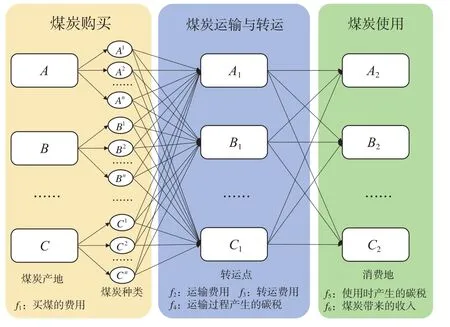
图1 煤炭运输示意图Fig.1 Schematic diagram of coal transportation

设f1为买煤的费用，f2为煤炭的运输费用，f3为煤炭的转运费用，f4为运输过程产生的碳税，f5为使用过程产生的碳税，f6为煤炭带来的收入。目标函数为f6-f1-f2-f3-f4-f5最大，即企业的利润最大。通过综合考虑煤炭价格、碳税、运输转运费用，为企业决策者确定煤炭采购方案、制定碳减排方案提供参考依据。

为了便于建模及求解，做出以下假设：①如果2个节点之间有多种运输方式，优先选择运输费用小的方式；②考虑到煤炭运输的特点和运输成本，以铁路和水路为主要运输方式，不考虑公路运输；③水运的通航能力比较富余，所以水路运输不做最大运量限制；④电费为整个过程的唯一收入；⑤煤炭运输过程中涉及多次换装，换装主要发生在不同运输方式的转运节点上，因此假设铁铁转运不需要转运费用，铁水转运需要转运费用[9]。

1.2 模型建立

在1.1问题描述与假设的基础上，以f6-f1-f2-f3-f4-f5最大为目标函数，以产地到消费地的运输量为决策变量，构建运输模型，如公式 ⑴ 所示 ，公式 ⑵ 至公式 ⑹ 为约束条件 。公式 ⑵ 表示消费地的煤炭总供应量折合成标准煤不小于其需求量；公式 ⑶ 表示铁路运输实际运输量不大于最大限制运输量；公式 ⑷ 表示产地销量小于等于生产量；公式 ⑸ 表示煤炭的转运量不能大于港口的最大转运能力；公式 ⑹ 表示所有变量均为非负。

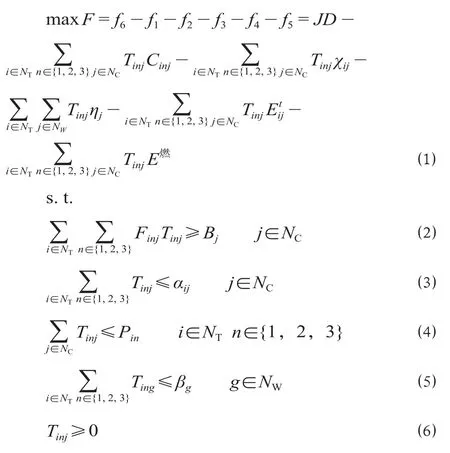
式中：Tinj为决策变量，表示消费地j从产地i购入第n种煤炭的量，t；αij为i到j运输的最大流量限制， t；χij为铁路线或水运航线的运输费率，即1 t煤炭在该铁路或航线上的运输费用，元/ t ；Etij为列车在铁路i到j或轮船在航线i到j产生的碳税，元/t；E燃为单位质量煤炭燃烧产生的碳税，元/ t；D为火力发电量，kW·h；J为电价，元/(kW·h)；βg为港口g转运量限制， t；ηg为港口g的转运费率，即1 t煤炭在港口的转运费用，元/t；Bj为消费地j需要的标准煤炭量，t；Pin为i地第n种煤炭的产量，t；Cinj为消费地j从产地i购入第n种煤炭的单位费用，元/t；NT为产地集合，i∈NT；NW为港口集合，g∈NW；NC为消费地集合，j∈NC。

1.3 模型求解思路

首先在此模型基础上构建煤炭运输交通线路与节点，之后通过查找相关资料获取交通线路上单位质量的煤炭运输价格、转运价格、运输过程中交通工具的碳排放量、碳税、电价等相关计算数据；其次考虑单位质量的煤炭运输过程中的费用，以f综= f2+ f3+ f4最小为目标函数，运用Python求解各煤炭产地的单位质量的煤炭到消费地的最佳路线，并得出单位质量的煤炭在运输过程中的综合费用f综；最后以F=f6-f综-f1-f5最大为目标函数，将问题转化为运筹学中的运输问题，运用Lingo求解煤炭产地与消费地的最佳匹配方案，最佳运输线路为用Python求解的最佳线路。

2 算例分析

选取江苏省南京市火力发电系统为研究对象，江苏省煤炭主要由山西、陕西、内蒙古三省(区)供给，选取朔州、大同、太原、长治、神木、包头、介休作为南京的煤炭供应点。常用的运输途径有2种：①煤炭从产地经过铁路运至秦皇岛、天津、青岛、日照、连云港等港口，转海运南下至上海，从上海通过长江水运到南京；②从产地经铁路直接运至南京，中途不需要转运[10]。煤炭运输网络图如图2所示。

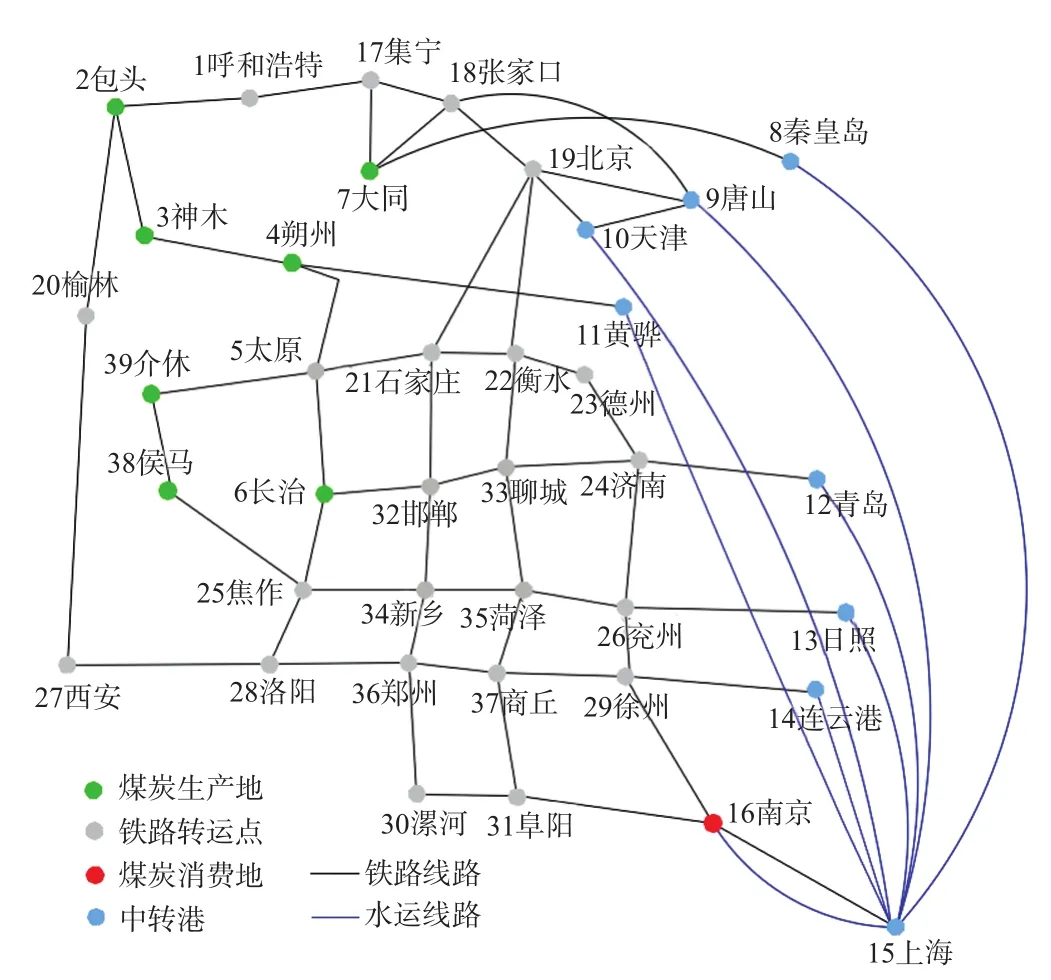
图2 煤炭运输网络图Fig.2 Coal transportation network

2.1 算例数据

根据1.2节模型，系统输入数据包括：铁路弧段的距离、节点间的运输与转运费用、碳排放量数据、煤炭产量与需求量数据，相关数据获取过程如下。

（1）铁路弧段的距离。铁路运输线路的距离通过查询各城市之间铁路车站里程信息获得，铁路节点之间的距离如表1所示。

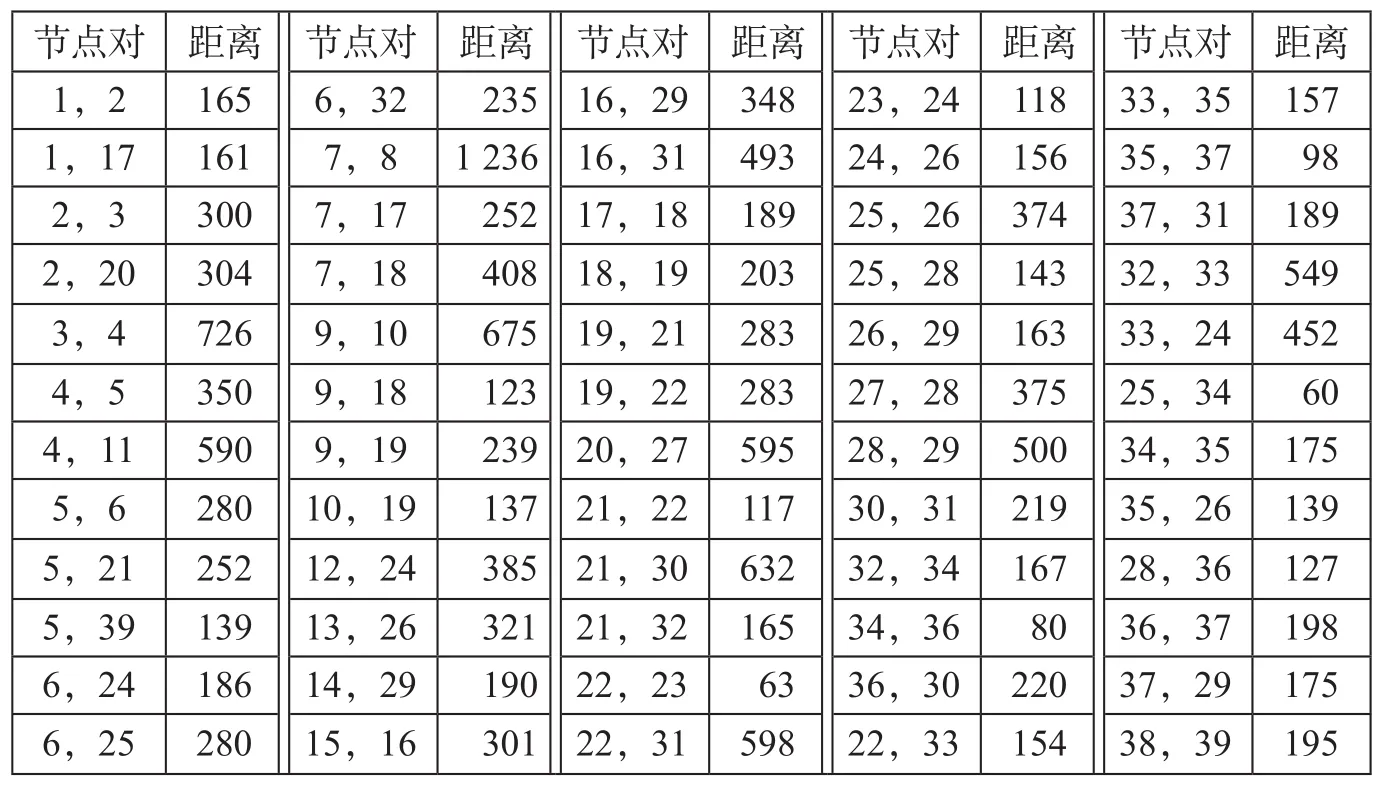
表1 铁路节点之间的距离 kmTab.1 Distance between railway nodes

（2）节点间的运输与转运费用。根据《铁路货物运输管理规则》[11]，铁路运价率取值为0.15元/(t·km)，铁路弧段的运输费用为运价率乘以运输距离。固定航线的水路运费参考中国沿海煤炭运价指数(CBCFI)，港口节点之间的水路运价如表2所示。煤炭铁路转水路需要港口转运费用，港口转运费用包括装卸成本、等待时间成本、储存成本，这里取转运费用的平均值6.15元/t[12]。

表2 港口节点之间的水路运价 元/ tTab.2 Waterway transportation price between port nodes

（3）煤炭产量与需求量数据。煤炭的产量数据通过收集近年来当地煤炭生产量获得；价格、发热量参考煤炭交易网上的数据。不同种类煤炭的发热量不统一，导致煤炭的利用价值不同，为了统一各种煤炭的利用价值，此处将各种煤炭换算成标准煤炭。标准煤系数按照Xin=Hin/H计算。其中，Xin为标准煤系数；Hin为i地生产第n种煤炭的热量，i∈NT，J/kg；H为标准煤炭的发热量，29 288 000 J/kg。煤炭的需求量数据根据城市一年的火力发电量所需的标准煤炭计算。

（4）碳排放量数据。铁路运输的单位碳排放量为8.86 g/(t·km)，水路运输碳排放量为7.58 g/(t·km)[9]，当前的碳税还没有统一的标准，各个国家收取碳税也有较大的差异，当前中国的碳税普遍不高于8美元/t，取参考文献[9]的数据，碳排放价格为60元/t。

为1 t产于i地的第n种煤燃烧时产生的二氧化碳吨数，计算方法[13]为：其中，Wcoal为燃煤量，t；C为煤含碳量，此处取收到基元素碳，%；MCO2为二氧化碳的摩尔质量，44 g/mol；MC为碳的摩尔质量，12 g/mol；OFcoal为燃煤机组氧化率，此处取98%。

煤炭产量信息如表3所示。

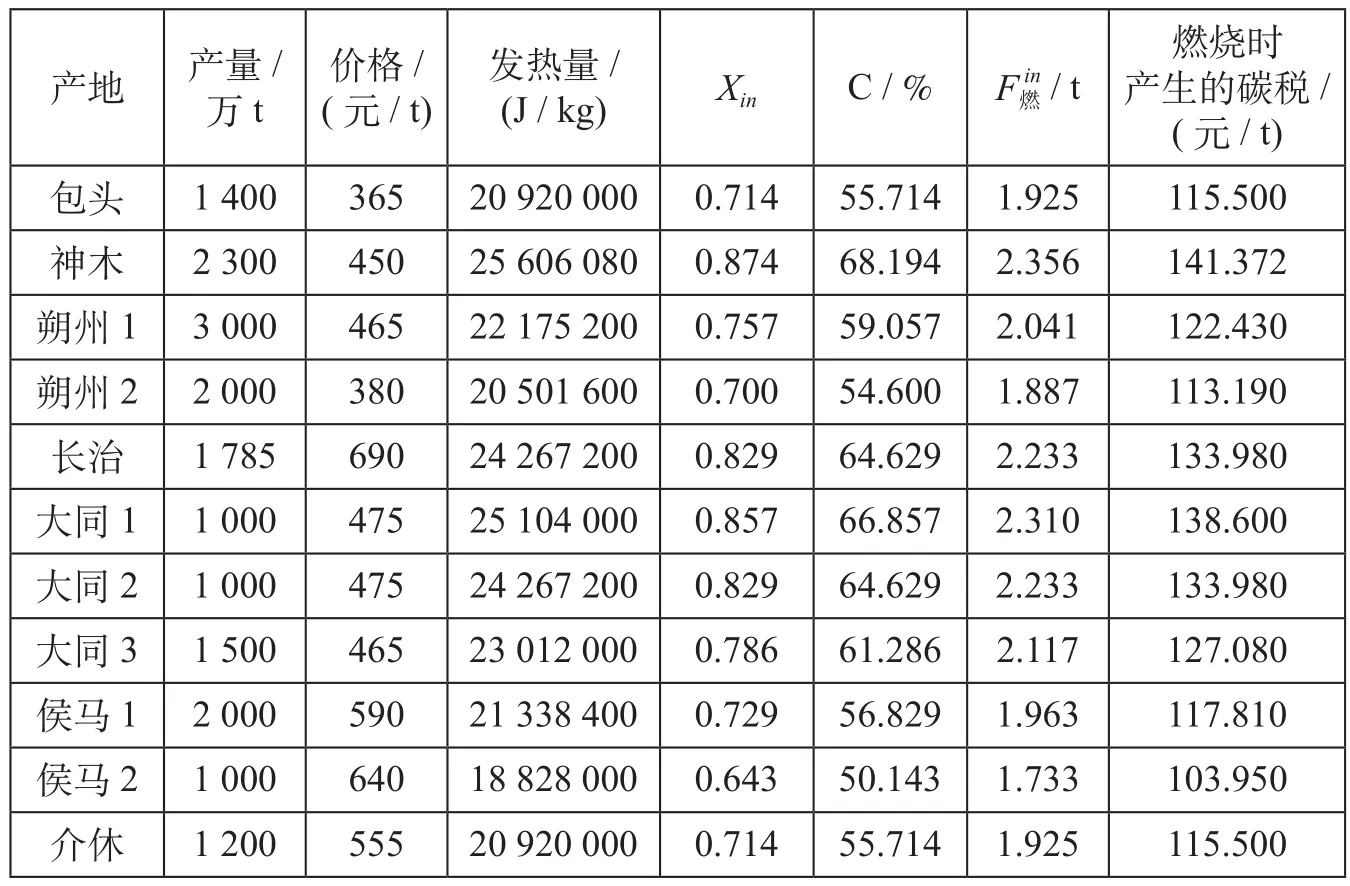
表3 煤炭产量信息Tab.3 Coal production information

2.2 算例求解

2.2.1 最优路径选择

单位质量煤炭的运输费用只与运输路径有关，因此首先求出各产地到消费地的最优路径，以f综=f2+ f3+ f4最小为目标函数，用Python进行编程求解，确定各产地到消费地的最优路径。f综是单位质量煤炭的运输费用、转运费用、运输过程中交通工具产生的碳税之和，相当于运输过程中所有花费。最优运输路径求解结果如表4所示。

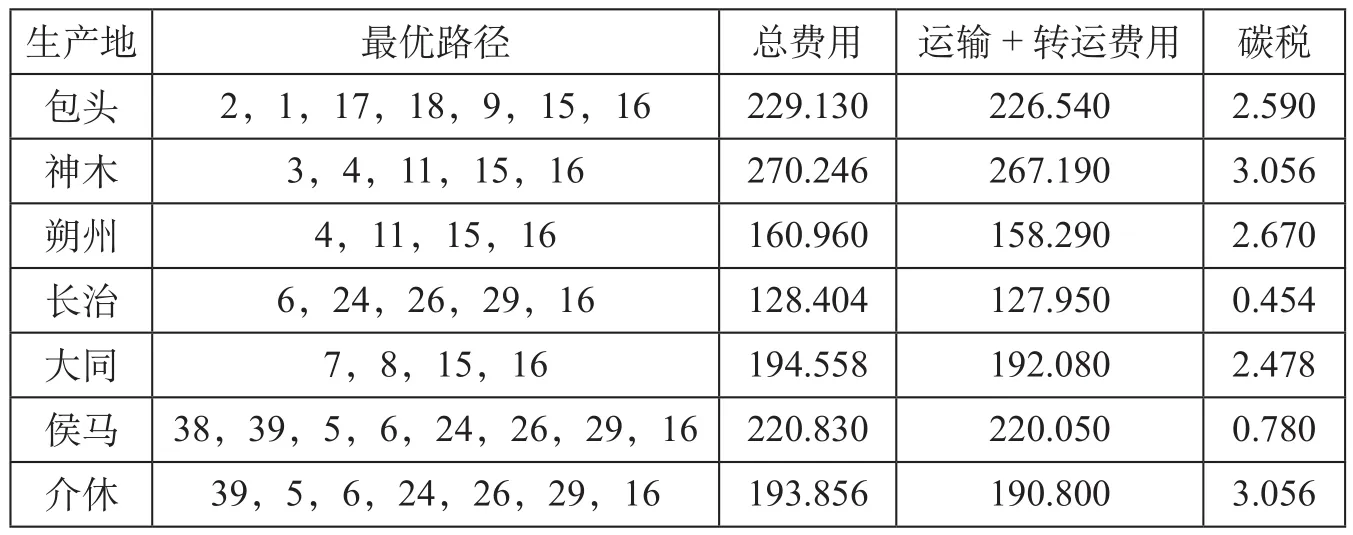
表4 最优运输路径求解结果 元/ tTab.4 Solution of optimal transportation route

2.2.2 煤炭采购方案

2020年南京市的火力发电总量约为500亿kW·h，假定南京市火力发电机组的平均容量为300 MW，该型号机组平均消耗标准煤大约为400g/(kW·h)，则发电量500亿kW·h消耗标准煤2 000万t；假定今后火力发电以每年10亿kW·h的速度增长，不同发电量消耗的标煤量如表5所示。

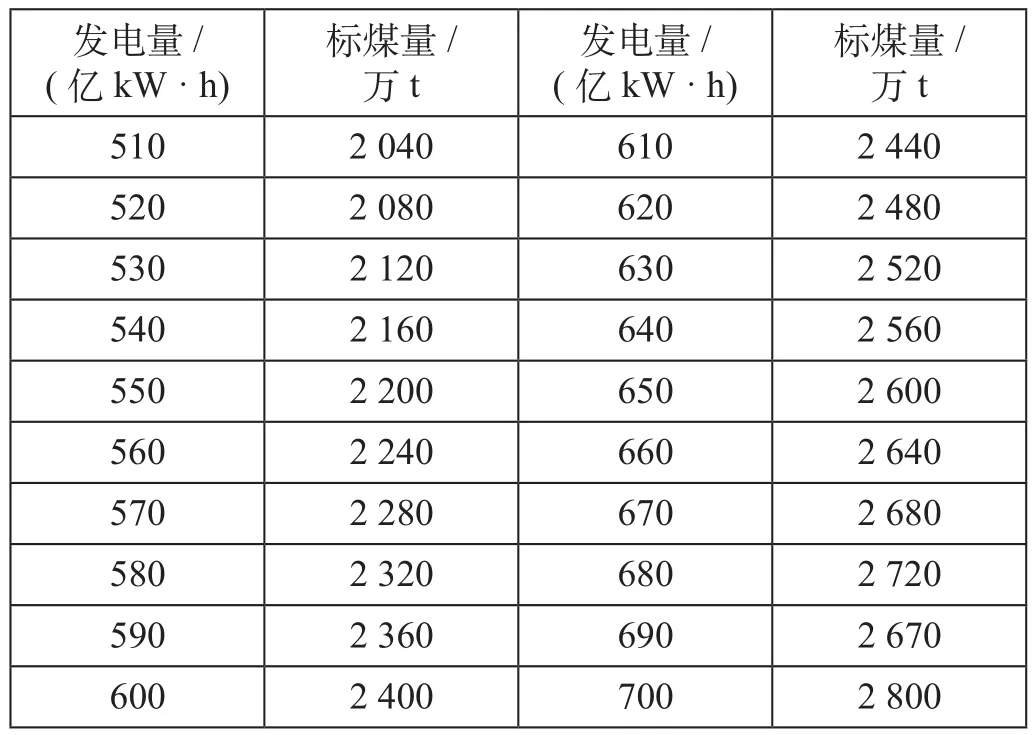
表5 不同发电量消耗的标煤量Tab.5 Amount of standard coal consumed under different power generation

对于不同的煤炭消耗量，以F =f6-f综-f1-f5最大为目标函数，用Lingo软件编程进行求解。其中，f6为煤炭带来的收入，为发电量乘以电价，电价按照南京市居民用电标准取 0.6元 /(kW·h)；f综在 2.2.1中已求解；f1为买煤的费用，为煤碳采购量乘以煤炭单价。最终计算得到不同煤炭需求量下的煤炭采购方案如表6所示。碳排放强度为每度电需要排放的二氧化碳量，根据每度电的碳税和2.1中的碳税单价，能够计算出碳排放强度。

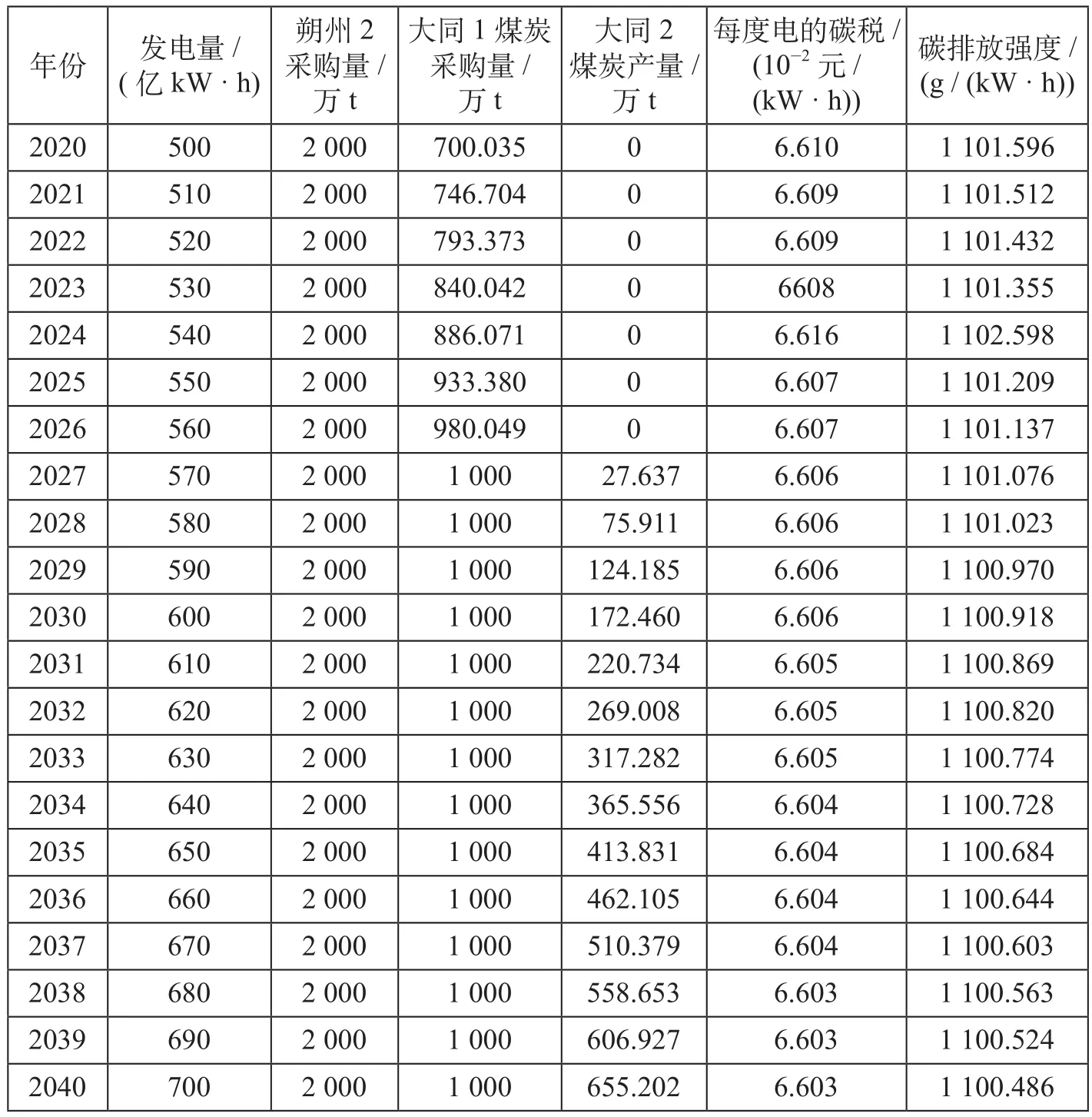
表6 不同煤炭需求量下的煤炭采购方案Tab.6 Coal procurement schemes under different coal demands

在煤炭产地产量稳定且发电量为500亿～ 560亿kW·h时，朔州2和大同1能够满足南京市火力发电的要求；发电量为570亿～ 700亿kW·h时，需要增加大同2作为新的煤炭供应点。此时，每度电的碳税约为0.066元，处于一个比较低的水平。这与碳税取值比较低有关，我国为发展中国家，需要大量能源保障经济发展，收取过高的碳税在一定程度上会影响我国经济发展的活力。发电量在500亿～ 700亿kW·h范围内，碳排放强度逐渐降低，碳排放强度的波动在1.5 g/(kW·h)以下。发电量与碳排放强度的关系如图3所示。我国发电量巨大，碳排放强度的微小波动会给碳排放总量带来较大的改变，同时也反映一个事实，即仅仅靠煤炭运输路径优化、选择“性价比”高的煤炭减少的二氧化碳量是有限的，在2030年前电力行业实现碳达峰需要更强有力的减排措施。

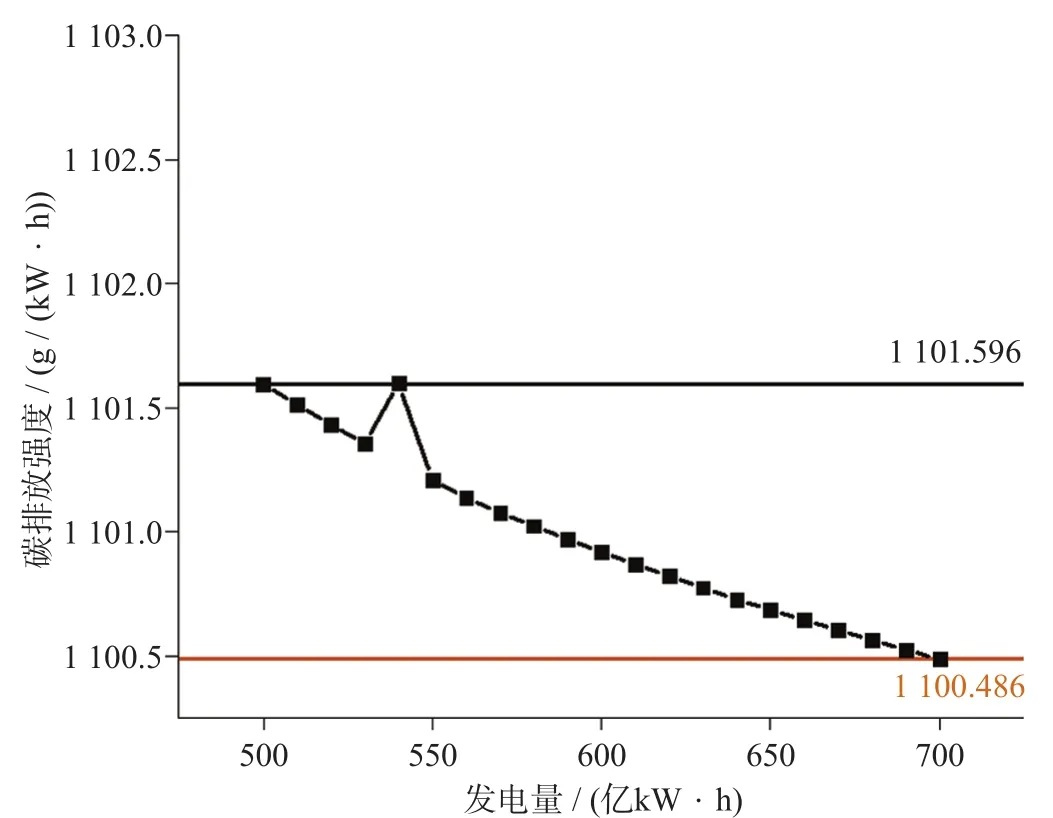
图3 发电量与碳排放强度的关系Fig.3 Relationship between power generation and carbon emission intensity

2.2.3 碳达峰分析

对案例中的运输费用、转运费用、收入、碳税占比等进行计算，得到不同火力发电量对应的费用如表7所示。可以看出，碳税(即f4+f5)占f1，f2，f3，f4，f5之和的 17.5% 左右，且处于一个比较稳定的值。如果火力发电按照当前的速度发展，二氧化碳排放量会持续增加。为实现2030年之前碳达峰目标，需要加快清洁电力发展的速度，常见的清洁电力有水电、核电、风电和光电，据统计当前南京市水电、核电、风电和光电发电量占全部发电量比重在20%左右，在此数据基础上，若要实现2030年之前碳达峰的目标，则清洁电力年平均发展速度可按照以下方法获取。

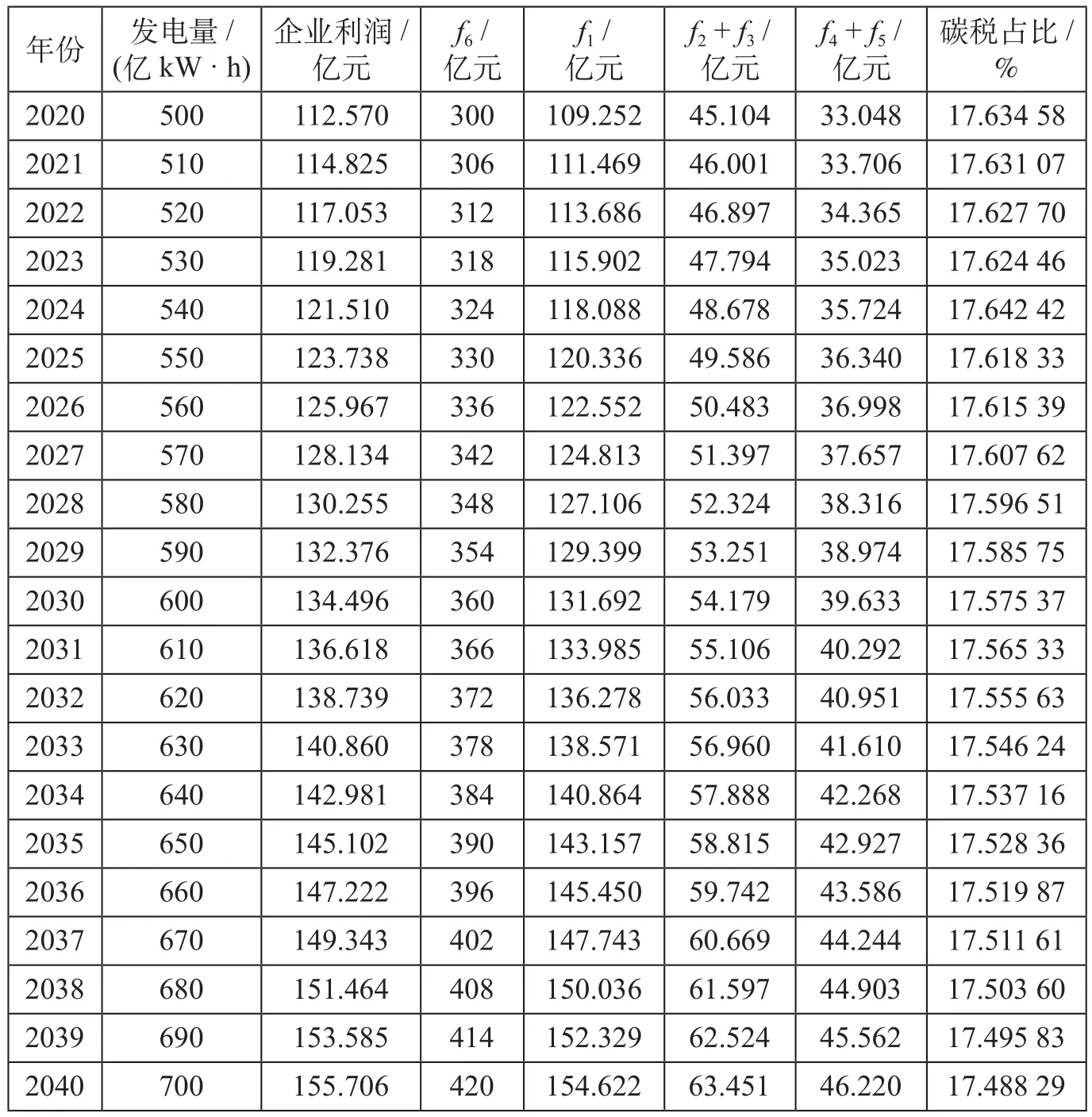
表7 不同火力发电量对应的费用Tab.7 Corresponding cost of different thermal power generation

（1）设定碳达峰满足的条件。清洁能源不断发展，清洁电力的比重会不断增加，当第t +1年的碳排放量小于第t年的碳排放量，并且之后的每一年都逐年减少时，则第t年实现碳达峰的目标。根据上述依据，给出清洁能源发展速度的计算方法如公式 ⑺ 所示。

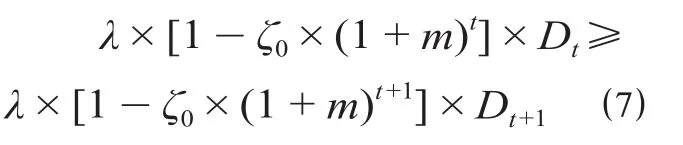
式中：λ为碳排放强度，根据表6的计算结果，这里取1 100 g/(kW·h)；ζ0为开始年南京市清洁电力占用电量的百分比，这里取20%；m为清洁电力的发展速度，%；Dt为第t年南京市用电总量，用电总量包括火力发电量与清洁能源电量，亿kW·h；t为碳达峰需要的年份，假设2021年初为第0年，2022年初为第1年，即经过2021年一年的发展，在2022年初实现碳达峰，同理2031初年为第10年，即从2021年初开始，经过10年的发展，实现碳达峰的目标。

（2）给ζ0，Dt，Dt+1赋予不同的值，分别计算2022年、2023年直至2031年碳达峰时，清洁电力(不限制于传统的风电、光电、核电，随着科技的发展，碳捕捉封存技术逐渐成熟，如果传统火力发电能实现完全零排放，火力发电也是广义上的清洁能源)年平均发展速度m。这里假设用电量以平均每年5%的速度增加，即Dt+1= 1.05×Dt，D0= 625亿kW·h，2021年，清洁电力所占份额ζ0= 20%。

根据公式 ⑺ 计算可得不同碳达峰年份下的清洁电力发展速度如表8所示，碳达峰的年份越靠后，清洁能源发展的速度越缓慢，即留给清洁电力发展的时间越多，清洁电力发展的最慢年平均增长速度为7.161%；碳达峰时间越靠前，要求清洁能源发展的速度越快，火电企业发展的压力越大，如2022年实现碳达峰，清洁电力的年平均发展速度为15.799%，根据国家统计局发布的数据，2019年我国前三季度，水电、核电、风电和太阳能发电量占全部发电量的比重为28.2%，比2018年同期提高1.5%，因此15.799%的发展速度会给相关部门带来较大压力。

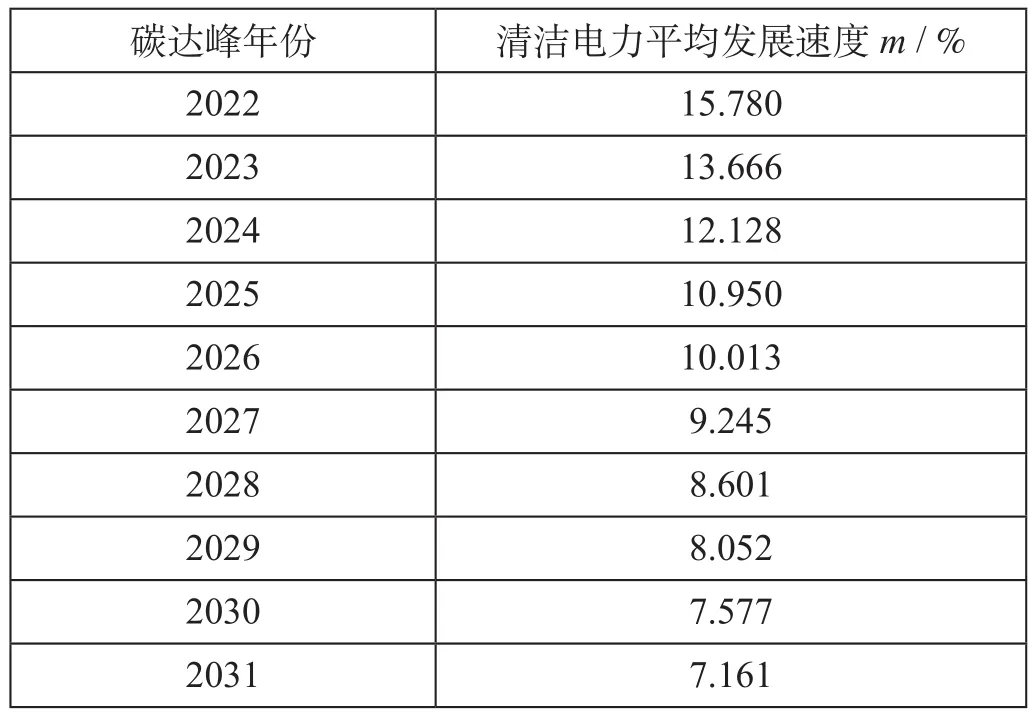
表8 不同碳达峰年份下的清洁电力发展速度Tab.8 Development speed of clean power in different carbon peak years

3 结束语

从火力发电企业的角度出发，综合考虑运输费用、煤炭采购费用、碳税、企业收入4个因素，以企业利润最大为目标函数，建立运输模型，用Python与Lingo对模型进行求解，以南京市为例进行分析，发现朔州2和大同1为南京市的最佳供煤点，随着电能需求量的增加，需要增加大同2为新的供煤点；不同需求方案下，碳税占整个花费的比例稳定在17.5%；同时发现南京市若在2030年前实现碳达峰的目标，清洁电力的年均发展速度至少为7.161%，以此估计南京市距离2030年实现碳达峰的差距，倒逼相关部门尽快制定减排政策，确保2030年之前实现碳达峰。本研究在电煤采购方面考虑了电煤的单价与碳排放强度，能够为火力发电企业电煤的采购提供参考依据，从源头上对火力发电的二氧化碳排放进行控制；在运输方面综合考虑运输费用与碳排放2个因素，对煤炭运输路径进行优化，选择费用最小的运输路径；对所选算例进行火力发电行业的碳达峰分析，探讨清洁电力发展的速度，为城市及企业碳达峰研究提供思路。