特高拱坝整体稳定安全度评价指标研究

胡 筱，张 冲

（中国电建集团成都勘测设计研究院有限公司，四川 成都 610072）

1 概 述

当前已建和在建的特高拱坝，如溪洛渡、锦屏一级、小湾、大岗山等，在拱坝结构设计分析中，普遍采用现有设计规范［1-2］中的强度安全系数评价体系。该理论体系认为高拱坝的破坏是由材料（坝体混凝土和坝基岩体）发生破坏造成的，如拉应力过大导致坝踵开裂，压应力过大导致下游坝肩、坝体屈服甚至溃坝，剪应力过大导致坝基岩体沿软弱结构面滑动等。因此可以通过极限状态下的材料抗力和设计荷载作用效应的比较，确定结构是否进入强度破坏状态，从而确立安全度。事实证明，造成拱坝失事的根本原因之一也是大坝实际应力超过了材料的强度。因此中国、美国、日本等国家目前均采用了该安全体系作为规范规定的安全评价体系。该体系优点在于意义明确，计算简单，有多年的工程实践经验，许多国家规范有与之配套的容许安全系数，因而容易为广大的工程科技人员所接受。该方法明显的不足就是，将局部破坏等同于整体破坏，没有把坝体、坝肩和坝基作为一个整体系统来考虑，因此该安全体系指标只能作为评价拱坝某个点或者某个局部区域是否开裂的指标，而无法评价拱坝坝肩整体系统真正的安全储备情况。大量实例表明，绝大部分拱坝坝面裂缝不影响拱坝的正常运行。因此，各国专家学者对拱坝安全度进行了大量的多方法研究，综合各类研究成果来看，拱坝安全评价方法整体上可分为四类。

（1）规范规定的材料强度安全体系［1-2］。该体系要求坝体混凝土、坝基基岩的设计应力不超过材料强度，保证材料不发生屈服或破坏。若材料发生局部破坏，即认为结构是不安全的。对于拉应力，通常直接给出容许拉应力值作为控制标准。该评价体系以拱梁分载法、线弹性有限元、线弹性有限元-等效应力法［3］作为基本评价方法。

（2）柔度指标评价体系。1986年，在柯恩布赖茵拱坝的修复过程中，Lombardi提出拱坝“柔度系数”的概念，来衡量拱坝在迎面水荷载的作用下变位的水平，并建议柔度系数应小于15，并根据统计规律，构建了Lombardi破损曲线。然而国内大量的拱坝统计规律表明，许多远远超过柔度系数15的拱坝工程依然处于正常工作状态。关于柔度系数的使用有过大量的讨论，拱坝设计规范的修编也一度被讨论是否纳入拱坝指标评价体系，任青文提出了修正的柔度系数表达公式［4］，将允许柔度系数与坝高关联起来；黄朝煊等提出了柔度系数上限的经验公式［5］，考虑了坝址地形地质条件因素。截至目前，各种研究和统计规律表明，利用柔度系数衡量拱坝整体安全指标，只能作为一种参考指标，尚不具备真正综合衡量拱坝安全状况的能力。

（3）地质力学模型试验安全评价体系［6］。此体系利用相似原理搭建拱坝-坝肩系统整体模型，通过超载分析（少量模型试验也采用降强分析）确立大坝所能承受的超载倍数，同时监测大坝模型的应力和位移变化情况。该方法的优点是直观，能完整地显示拱坝开裂、破坏的全过程，给出一个宏观的安全指标；其缺点是很难找到能够完全符合相似率要求的模型材料，且试验周期长、费用高。国内周维垣等［6］做了大量的高拱坝地质力学模型试验，归纳出影响大坝整体稳定的几个关键控制指标，即：起裂超载系数K1，非线性变形超载系数K2，极限超载系数K3。该指标体系目前已经大量运用在特高拱坝的设计分析研究中。

（4）拱坝坝肩整体稳定安全评价体系。拱坝作为超静定结构，实际运行过程中局部屈服开裂往往难以避免，但只要破坏程度不足以影响拱坝-坝基系统的整体稳定，拱坝仍可正常运行。整体稳定安全评价将大坝与坝基作为一个系统进行研究，需考虑坝体混凝土和坝基岩体进入非线性工作阶段后大坝-坝基系统内力的非线性调整，属于变形稳定分析。由于拱坝整体安全评价允许局部破坏，因而能充分利用材料的后屈服强度和拱坝超静定结构的特点。该评价体系以非线性有限元作为主要分析手段，其他非线性数值分析方法如离散元法、DDA、数值流形等数值方法也经常使用。在分析过程中通常采用超载倍数或者强度降低倍数作为安全评价指标。

工程实践表明，高拱坝是一种高次超静定结构，其在周边的严格约束下，对超载或变形的反应不敏感。整体安全度评价体系，充分反映了拱坝局部应力屈服或者开裂情况下，拱坝内力调整适应的特点，能充分模拟大坝开裂、屈服、失稳的整个过程，是目前发展势头迅猛的拱坝安全度分析方法。但目前整体稳定分析存在数值计算稳定性、混凝土及基岩本构模型的准确性、复杂结构模拟、评价指标选取等各个方面的差异，各类成果之间相互不能统一，且结果离散型较大。

本文重在提出一套基于整体稳定分析的特高拱坝安全评价指标，并与本人另文阐述的基于规范规定的常规评价体系一起，构建从材料点安全强度到拱坝整体稳定安全的综合评价体系。

2 拱坝整体安全度

整体稳定安全评价将大坝与坝基作为一个系统进行研究，需考虑坝体混凝土和坝基进入非线性工作阶段后系统内力的非线性调整，属于变形稳定分析。同时拱坝作为超静定结构，实际运行过程中往往局部出现屈服甚至开裂，但只要破坏程度不足以影响拱坝-坝基系统的整体稳定，拱坝仍可正常运行。因此，用点安全度衡量拱坝-坝肩整体系统的安全性就无法反应拱坝的真实安全裕度。而关于拱坝整体安全度，目前尚没有一个明确的定义。

在进行拱坝-坝肩系统抗滑稳定安全度评价时，目前较常使用的是超载安全系数和强度储备安全系数两种方法。然而不管采用何种方式，都缺乏一套行之有效的失效指标判断体系。

本文综合众多专家学者的意见，同时参考GB50199—1994《水利水电工程结构可靠度设计统一标准》［7］中关于极限状态的两种分类：承载能力极限状态和正常使用极限状态，初步提出了衡量拱坝-坝肩系统整体失效的两类指标，即：①结构性失效指标，比如位移失稳、大面积受压屈服、坝肩滑裂体稳定安全系数小于1.0等，出现此类情况说明坝已经被破坏，基本无法修复或者修复难度太大；②功能性失效指标，比如坝体位移过大、局部出现屈服等，出现此类情况说明坝体已经出现病态，不能完全满足使用要求，需进行修复。表1给出了失效指标和《标准》中极限状态分类的对应关系。功能性失效指标通常要小于结构性失效指标，因此用不同的失效指标去衡量拱坝-坝肩系统，得到的安全系数往往也是不同的。

表1 失效指标对应关系

经审慎分析选取，本文采取如下指标界定结构性失效。

（1）位移时程曲线的收敛性指标。拱坝-坝肩系统的失稳与否往往可以用某些关键块体的位移时程曲线来衡量，当系统处于稳定状态时，不管对于坝体的关键块体还是坝肩的关键块体，时段末的位移收敛都是必要条件，如果出现位移失稳即位移时程曲线不收敛，则认为拱坝-坝肩系统出现结构性破坏，因此本文将其划归为结构性失效指标。在非线性有限元计算中，通常表现为计算不再收敛，而在其他可以模拟大变形的非连续介质力学等方法中，通常表现为位移发散。

（2）坝肩滑裂体稳定安全系数指标。由于拱坝-坝肩系统中坝肩的稳定是整体稳定运行的关键，因此可借助极限平衡公式对拱肩滑裂体进行额外监测，如果静力稳定后或动力地震完成之后，坝肩滑裂体稳定安全系数小于1.0，则认为拱坝-坝肩系统出现了结构性失效。

（3）坝体应力及屈服指标。同功能性失效指标，当坝体受压屈服区贯穿或坝踵受拉屈服区与坝趾受压屈服区贯穿，均被视为拱坝坝肩系统发生结构性失效。

本文选取的功能性失效指标有以下几个。

（1）坝体稳定位移判断指标。拱坝-坝肩系统的破坏涉及到不同尺度的开裂机制，通常表现为黏塑形变形—弹性变形—黏弹性变形—屈服—开裂—失稳等多个渐进的阶段。在这个过程中，如果控制点位移出现明显拐点的，则拐点对应的超载倍数是衡量拱坝安全裕度的重要指标，然而大量分析计算表明，也存在一些难以找到拐点的情况，在这种情况下，建议采用挠度判断，在大跨度桥梁以及工民建梁板的分析中，通常要求挠度满足设计规范，如挠度小于L／600，L为跨度。本文借鉴该基本概念，以拱跨作为基本结构，要求整体挠度变位小于L／1000（可商定标准），认为系统如果超过该变位，虽然结构安全，但已经达到功能性失效指标。

（2）坝体压应力及屈服判断指标。拱坝设计的主要任务，是充分发挥混凝土抗压性能来传递坝面荷载，并尽量减小拉应力，从而减少拉应力区。因此，拱坝主要是一种受压结构，且最大压应力通常出现在上游拱冠梁中部高程及下游坝趾及建基面附近区域。当系统最大主压应力区达到受压屈服时，可以认为拱坝-坝肩系统达到了功能性失效指标。

（3）坝体拉应力及屈服判断指标。拱坝不可避免存在拉应力区，尤其在上游坝踵区域。本文认定，当坝踵拉应力屈服区深度达到帷幕位置所对应的水荷载超载倍数时，将其作为功能性失效指标。

（4）结构面滑移判断指标。坝肩稳定是拱坝整体稳定的关键，一旦结构面产生危害性的错位滑动，通常被认为拱坝彻底丧失承载能力。实践证明，马尔帕塞拱坝就是坝肩结构面在坝肩推力和渗透压力作用下产生错位滑动引发的。在大坝运行过程中，如果结构面拉应力（剪应力）超过该结构面抗拉强度（抗剪强度）时，缝面会张开（剪断），从而释放拉应力（剪应力），由于坝体局部受拉或者受剪出现少量的裂纹是完全可能的，因此本文没有采用拉应力作为判断指标，取而代之以结构面滑移作为判断指标。在非线性有限元计算中，应重点校核地质结构面上的点安全度指标，同时分析低安全度范围与帷幕的关系，对于非连续介质力学方法，如离散元、DDA等，建议计算结构面的滑移位移，检查缝面滑移是否贯穿整个结构面，是否贯穿帷幕。本文认为，如果大坝的坝肩设计蓄水位高程以下的结构面出现了上下游贯穿破坏，则认为大坝丧失挡水功能，出现功能失效。同时，如果在超载过程中，结构面错动位移曲线出现拐点，位移迅速增加，也是判断坝肩功能失效的重要标志之一。建议考虑该影响因素时，模型应能真实模拟结构缝，而非简单的单元材料等效。可供参考的方法有非线性有限元中的接触模型以及一些非连续介质力学方法。本文将结构面贯穿划归为功能性失效指标。

基于以上几点，以及一些具体的细节，只是作者研究工作的一点浅见，是否可行，还有待检验，并希望与大家讨论。

3 拱坝整体安全度分析

中国电建集团成都勘测设计研究院有限公司联合清华大学等单位，利用非线性有限元及超水容重的超载方法，研究了溪洛渡、锦屏一级、大岗山、二滩、小湾、拉西瓦等国内特高拱坝工程系统整体安全度。本文结合上述指标对成果进行了分析整理。

3.1 位移稳定分析

研究显示，正常荷载工况下（自重＋上游正常蓄水位＋下游水位＋泥沙压力＋渗流＋温降），拱冠梁顺河向位移最大值在80～180mm范围内，分布在拱冠梁顶部高程或近顶部高程。拱冠梁顺河向位移最小值在拱冠梁底部高程。位移差值在70～150mm之间，顺河向位移基本呈对称分布（见图1）。超载过程中，顺河向位移的分布规律基本保持一致；在约1.0P0～3.5P0低倍超载时，拱冠梁顶点、坝体底部及坝体最大位移基本为线性增加，说明拱坝整体处于弹性工作状态。随着水载倍数增加，顺河向、横河向变位进一步增大，个别拱坝表现出非线性增长特征（以二滩拱坝为例），如图2～3所示，位移增幅加大，表明局部屈服导致拱坝自身重新调整，应力实现重分布。

图1 拱冠梁位移和坝高的关系

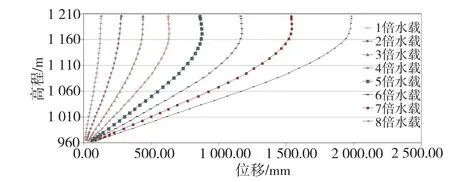
图2 二滩拱坝超载情况下拱冠梁顺河向位移分布

图3 二滩拱坝监测点位移-超载倍数关系曲线

部分拱坝监测点位移未能表现出期待中的非线性特性，然而研究显示，当水荷载超载系数达到4.0～5.0时，其拱跨挠度普遍超过了本文约定的L／1000的上限（见表2），且利用位移拐点判断的超载倍数与利用挠度判断的超载倍数大致相当。其中，小湾拱坝由于河谷较宽，达到允许挠度的超载倍数稍小。

表2 国内6座特高拱坝稳定位移超载倍数

数据研究显示，采用非线性材料本构模型，由于坝体逐渐屈服，当荷载加载到7.0～9.0时，大坝逐渐失稳，变现为计算不再收敛，本文认为达到结构失效。

3.2 应力及屈服区失效判断

正常荷载状态下，特高拱坝坝体可以划分为4个区，分别为：上游三向受压区，主要为80%以上上游中间坝面；上游拉压应力组合区，靠近建基面宽约20～30m条带，最大宽度一般不超过坝高的1／5；下游拱端拉压组合区，主要在坝中部附近到坝底，宽度约1／4坝高；下游中间低应力三向受压区。

研究表明，正常荷载下，特高拱坝最大压应力在-7.0～-11.0MPa之间，通常出现在上游坝面拱冠3／5坝高附近或者下游拱端，前者处于三向受压区，混凝土强度受多轴效应后获得提升，后者处于三轴拉压应力组合区，混凝土强度较低，安全系数偏小，实践证明该区域最容易发生裂缝，数值分析也表明，该区域通常最先屈服。

利用非线性有限元研究发现，在超载过程中，随着水荷载的增加，当超载到1.5～2.0时，上游坝踵发生了明显的张拉屈服，屈服深度接近于帷幕位置，部分拱坝下游坝趾也出现了受压屈服。当超载系数达到2.0～3.0时，大量拱坝下游坝趾均发生受压屈服，同时上游坝踵受拉屈服区继续往下游方向扩展，到3.0时，拱冠梁底部上下游屈服区基本贯通。而大量的研究表明，拱坝上游中部高压应力区，由于处在三向受压状态，即使出现了明显的应力增加，依然难以屈服，在5.0以下，通常难见该部位有屈服区，而数值分析表明，该区域此时的压应力甚至已经达到并超过了混凝土的单轴抗压强度。表3统计了6座特高拱坝不同区域屈服所对应的水荷载超载倍数。从统计规律基本可以判断，对于300m级特高拱坝，当水荷载超载倍数达到1.5～2.0时，上游坝踵屈服区深度接近于帷幕深度，拱坝-坝肩系统达到功能性失效状态。当超载倍数达到3.0时，拱冠梁底部屈服区贯穿，本文认定为结构性失效（见图4）。同时需要补充说明的是，随着超载倍数的增加，下游坝面的屈服区向坝内方向延伸，各高程水平拱圈首先在下游侧发生屈服，进而使得作用力轴线往上游方向偏移，从而进一步加大上游面的压应力，最终引发上游面受压屈服，并使得整个屈服区贯通。

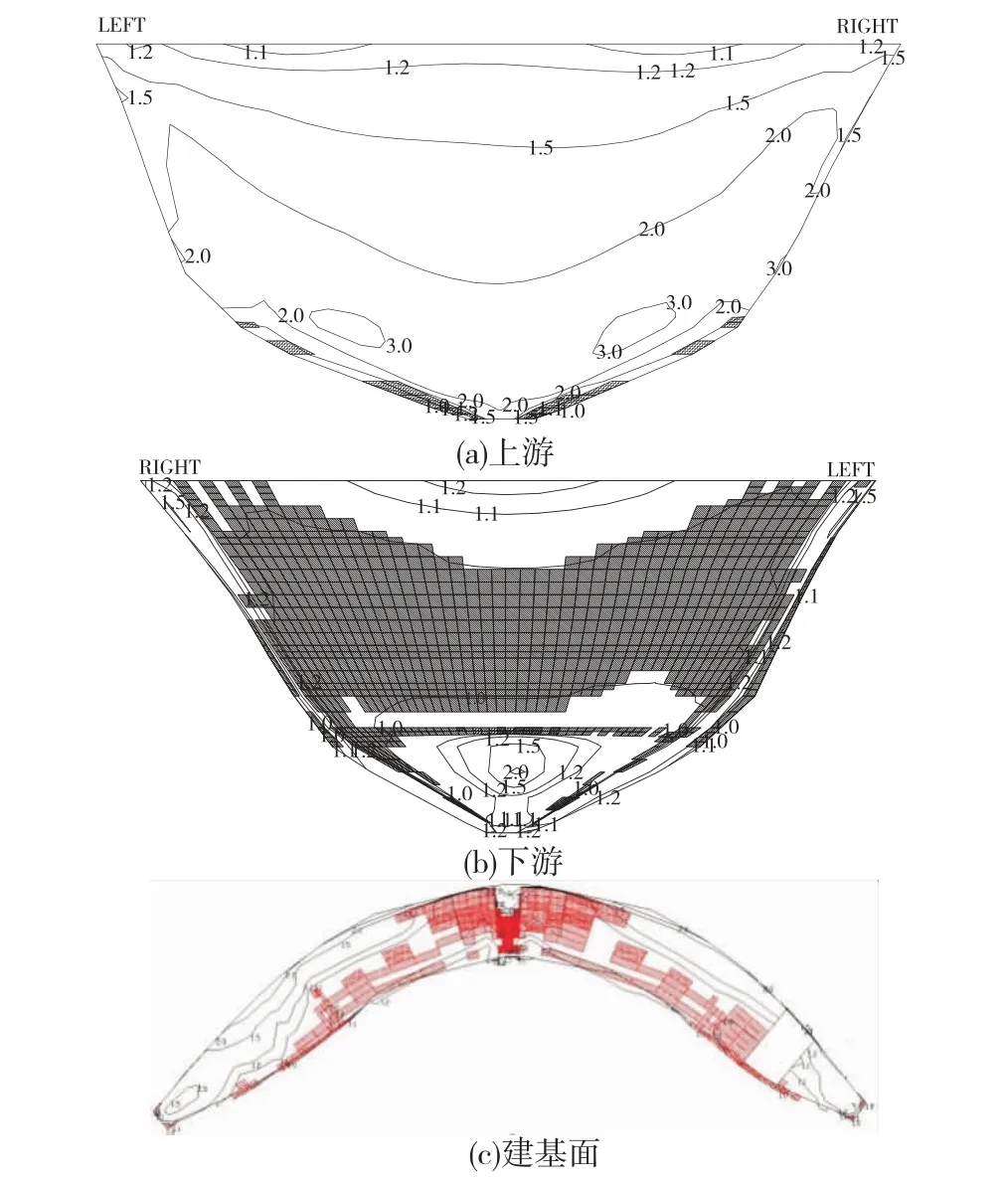
图4 溪洛渡拱坝超载倍数3.0时，屈服区分布

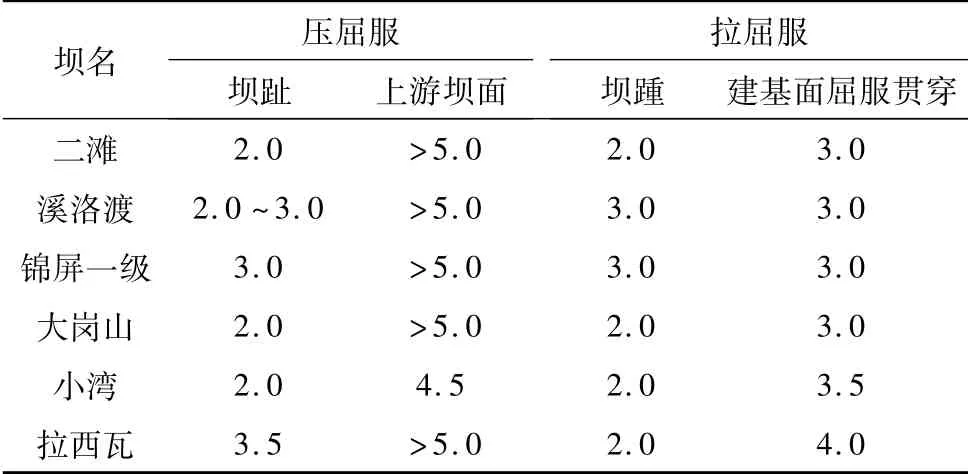
表3 6座特高拱坝拉压屈服超载倍数（以0.5P为加载倍数，依次递增）

3.3 坝肩抗滑稳定安全分析

坝肩稳定是整个拱坝安全稳定的关键，各国规范均对拱坝坝肩抗滑稳定提出严格要求，我国拱坝设计规范要求拱坝坝肩抗滑稳定安全系数不小于3.5。然而该安全系数是指采用刚体极限平衡法，利用抗剪断公式（见式1）应该达到的安全系数。

本工程采用二管高压喷射灌浆进行基础的防渗处理，墙体交接形式为摆喷折线搭接，墙体最小厚度不小于15cm。试验区按监理及设计要求选定，坝轴线上设置2孔，围井高喷孔1孔，共计3孔。本试验设计墙体交接形式为摆喷折线搭接，孔距1.4m。在墙下游侧修建围井，旋喷桩及围井布置结构形式如图3、图4。

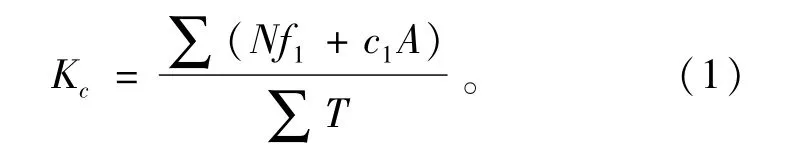
然而从方法论上看，刚体极限平衡的缺点在于：①研究坝肩稳定时将拱坝与支撑岩体分割开来，用运行期拱坝传给地基的荷载代替了拱坝，无法实时在拱坝与坝肩之间进行力的传递；②无法模拟坝肩岩体大变形、坝肩结构面张开或滑移；③无法将拱坝自身的应力状况与坝肩的状态一一对应起来，无法判定坝肩结构面张开或者滑移时拱坝处于怎样的应力状态；④作用在坝肩滑裂体上的拱坝推力是定值，无法考虑拱坝应力重分布；⑤无法给出直观的拱坝-坝肩系统整体破坏的过程仿真。

同时对某些工程而言，尽管坝址岩体条件良好，并将建基面全部置于微新岩体上，抗滑稳定安全系数也不能满足大于3.5的要求。例如，溪洛渡坝肩关键滑块的抗滑安全系数3.2，锦屏一级拱坝关键滑块的抗滑安全系数更低，为2.5。即使建基面进一步深嵌，也不能使抗滑稳定安全系数有较大的提高。究其原因［8］，不难从公式（1）中看出：拱坝拱推力∑T随坝高约呈2.5～3次方增加，而抗力中的∑C1A随坝高仅约呈平方关系增加。显然，对一般高拱坝而言，∑C1A的贡献相对较大，并且坝越低权重越大，要求KC≥3.5是根据当时工程经验规定的要求，用在特高拱坝就难于满足。

笔者曾将抗剪断公式引入三维变形体离散元中，并用以分析溪洛渡拱坝地震作用下坝肩最危险滑块的抗滑稳定安全系数［9］，同时为了真实模拟结构面性态，要求结构面一旦被拉开或者部分剪切破坏，就将该区域凝聚力c赋0值，因此，真实的安全系数介于抗剪安全系数和抗剪断安全系数之间（见图5～6）。结果显示［10］：①地震初期，在静荷载作用下，部分结构面已经张开，使得安全系数降低到2.1左右；②地震过程中，往复荷载会导致系统瞬时安全系数降低，但即使地震加速度幅值达到0.92g，最小安全系数依然大于1.0，坝肩滑裂体保持稳定，同时左岸略小于右岸；③地震结束后，抗滑稳定安全系数较地震初期略有降低，但依然在2.0以上，并保持结构稳定。

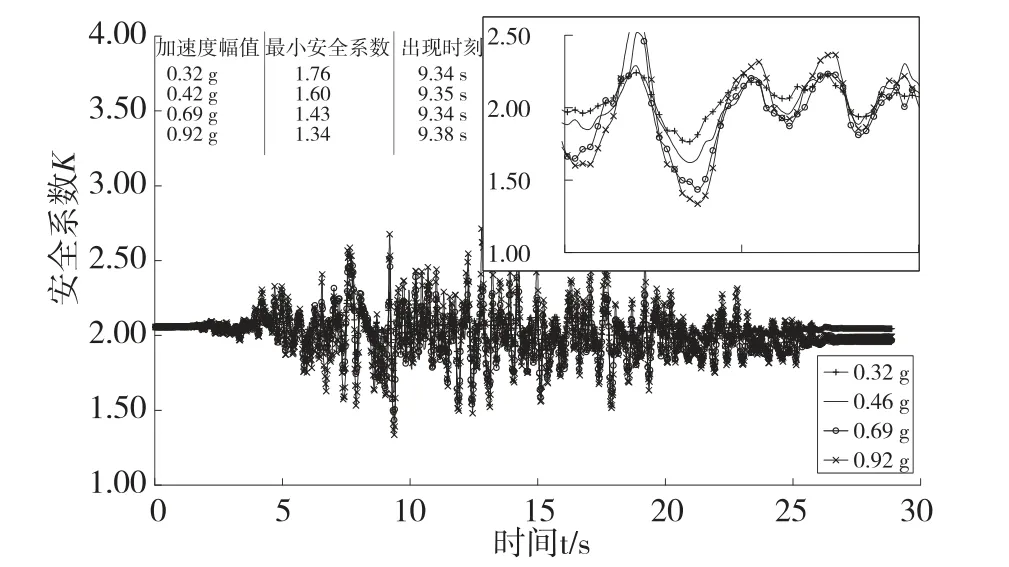
图5 左岸坝肩最危险滑裂体安全系数时程曲线

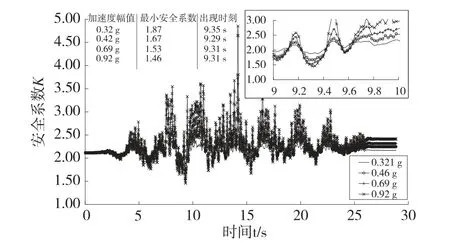
图6 右岸坝肩最危险滑裂体安全系数时程曲线

3.4 结构面开裂滑移

拱坝坝肩结构面开裂滑移分析一直是拱坝-坝肩整体稳定分析中的难点之一，目前的有限元模型，绝大部分采用材料非线性近似等效几何非线性问题，从而求解结构面的应力分布和屈服状态，进而反映相应部位的点安全系数。随着数值分析方法的进步，非线性有限元法模拟几何非线性的能力逐渐提升，同时非连续介质力学方法的长足进步，如三维离散元、DDA等，为真实模拟拱坝坝肩结构面提供了新的方法和手段。

图7利用非线性有限元法给出了大岗山拱坝在超载工况下各关键断层和接触带的错动变形情况。分析认为，断层和接触带主要以错动变形为主，变形错动最大部位主要集中在坝肩附近。断层f84、β21接触带变形较大。当水荷载超载倍数达到1.5P0～2.0P0时，各关键断层的错动位移均出现明显非线性增长，尤其是f84，当超载倍数达到3.0P0时，错动位移已经达到10.77cm。因此，可以初步认定，大岗山拱坝超载倍数达到1.5～2.0时，系统发生功能性失效。

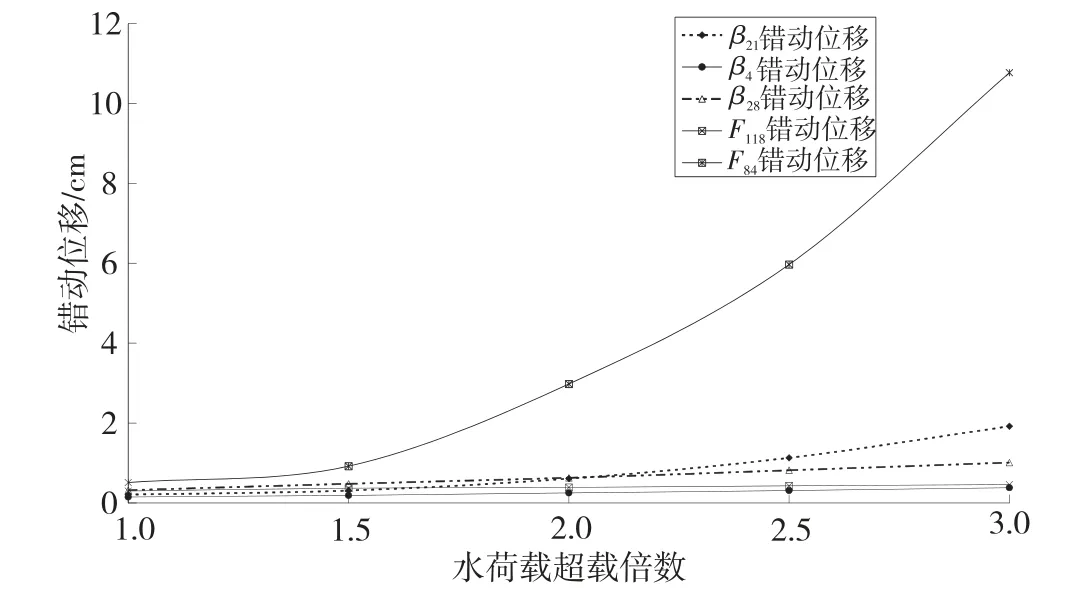
图7 大岗山拱坝关键断层错动变形

4 结论与存在的问题

上文利用本文提出的拱坝整体稳定安全评价指标对国内6座特高拱坝的整体稳定安全状况进行了初步论述，充分证明了利用本文提出的2大类7小点安全评价指标论证拱坝整体安全度是可行的，可以反映拱坝-坝肩系统的安全状况。

研究显示，特高拱坝的失效通常表现为如下几个过程。

（1）当特高拱坝超载到1.5P0～2.0P0时发生功能失效，综合表现为拱坝坝踵区域屈服区达到帷幕位置、坝肩结构面错动位移产生突变，大坝渗漏量将加大，部分丧失挡水功能。

（2）其次，整个大坝在3.0P0～4.0P0时，位移呈非线性加速增加态势，允许位移达到并超过本文规定的允许挠度，坝踵区域受拉屈服区域与坝趾区域受压屈服区域贯穿，上下游坝面屈服面积迅速增长。此时大坝变形对于各类设备运行的影响尚未有相关的研究。大坝进一步功能失效。

（3）再次，当大坝超载到7.0P0～9.0P0时，非线性有限元计算成果出现不收敛，大坝开始位移失稳，拱坝坝肩系统达到结构失效。

由于暂时未能在三维非线性有限元方法体系里，对超载过程中的坝肩抗滑稳定安全系数进行监测，故暂时无这方面的成果。

当然，目前的拱坝-坝肩系统整体安全稳定分析除了分析评价指标外，还存在诸如分析方法、标准化分析流程等各方面的问题，导致计算给出的表观安全度与拱坝-坝肩系统整体安全度尚有一定的差距。

笔者认为，目前的拱坝-坝肩系统真实安全度评价还存在如下问题。

（1）难以将有效的评价系统整合到统一的方法中，比如非线性有限元法擅长模拟复杂结构的变形和位移，然而其对大量断层、结构面的处理依然差强人意；离散元法可以有效模拟各类复杂结构面，然而其材料本构模型偏少，计算成果受结构面刚度选取制约较大；可喜的是，笔者看到有些有限元软件已经成功嵌入了离散元等非连续介质力学模块，从而为同时真实反映结构非线性和材料非线性奠定了基础，有助于拱坝-坝肩系统真实安全度的研究和评价。

（2）真实的拱坝运行过程中，其坝身全级配混凝土的受力多处于复杂应力状态之下，由单轴抗压、抗拉试验所得的结果不能完全反映实际结构中混凝土的强度及变形特征。试验研究揭示，当混凝土处于多轴拉压状态，混凝土的抗压强度、抗拉强度均低于相应的单轴强度，而当混凝土处于多轴受压状态，混凝土的抗压强度将高于单轴抗压强度。目前的混凝土本构绝大部分采用D-P准则，尚未考虑混凝土多轴效应的影响，部分考虑了多轴效应的本构模型，如william-warnke模型等，未能取得足够实用化的突破。因此本构模型与混凝土实际变形屈服过程还具有相当大的差异。

（3）目前，在进行拱坝-坝肩系统静力抗滑稳定安全度评价时，较常使用的是超载安全系数、强度储备安全系数或者混合法三种方法，其中超载法又分为超水容重法和超水头法，尚未形成统一的标准，因此得出的安全系数评价结论也具有较大的离散性。笔者偏向于采用在静力分析中超水容重的超载安全系数评价拱坝-坝肩整体稳定，其原因在于该法在超载过程中，整个水荷载等效成集中荷载后，集中荷载的作用点不发生改变，因而能始终保持拱坝受力结构的相似性，从而准确反映各部位的实际承载能力和对应的安全裕度。

（4）当前规范规定的基于常规评价方法的点安全系数评价系统与拱坝-坝肩整体稳定安全评价系统是两套彼此独立的安全评价标准，目前尚未建立起两套安全评价体系之间的联系。