噪声鲁棒的高光谱图像波段选择方法

路燕，任月，崔宾阁

山东科技大学 计算机科学与工程学院,山东 青岛 266590

1 引 言

高光谱传感器以数十至数百个连续且细分的光谱波段对目标区域同时成像，形成了包含数十至数百个波段的高光谱图像（HSI Hyperspectral Image）（张良培和李家艺，2016）。由于包含丰富的光谱和空间信息，高光谱图像被广泛应用于各种任务，如复杂环境下的地物精细分类（Thenkabail和Lyon，2011；崔宾阁 等，2019）、目标检测（Nasrabadi，2014；Zhu 等，2019） 和植被面积估计（Lees，2020）等。高维度的光谱数据在为图像处理提供更多光谱信息的同时，也带来了维数灾难、信息冗余、计算复杂度高和存储成本巨大等问题（Fauvel 等，2013）。因此，维度约减已成为高光谱图像处理的一个重要环节（Zhao和Du，2016）。

高光谱图像降维方法通常可以分为两类：特征提取和波段选择（Cui 等，2020）。特征提取是根据某种准则将高维数据映射到一个特定的低维特征空间中，并提取新的特征值来表示原始高维数据（Sun 等，2014；Dópido 等，2012）。典型的特征提取方法包括主成分分析PCA （Principal Component Analysis）（Chang 等，1999）、独立成分分析ICA（Independent Component Algorithm）（Wang和Chang，2006）、线性判别分析LDA （Linear Discriminant Analysis）（Bandos 等， 2009； Zhai等，2019）和局部线性嵌入LLE（Locally Linear Embedding）（Li 等，2012）等。经过上述的空间变换，原始高光谱图像波段的物理含义发生了变化，并且丢失了一些关键信息（Yang 等，2012）。与特征提取方法不同，波段选择是从高光谱图像中选择出信息量较大、相关性较弱、类别可分性较好的波段组合，因而基本保留了地物的固有物理属性（Wang等，2018）。常用的波段选择方法有基于排名、基于搜索、基于聚类、基于稀疏性、基于嵌入学习和基于混合方案等（Sun和Du，2019）。

基于聚类的波段选择方法是高光谱图像降维的重要方法（Sun 和Du，2019）。该方法首先通过聚类将原始波段分组，然后从每组中选择一个代表性波段。最早的高光谱图像波段聚类方法是基于Ward 链接的分层聚类（Martínez−Usómartinez−Uso 等，2007）。之后，基于聚类的各种高光谱图像波段选择方法陆续被提出，如Rodriguez 和Laio（2014）提出基于密度峰值的快速聚类算法FDPC（Fast Density−Peak−based Clustering），该算法通过计算每个样本的局部密度和组内距离来识别聚类中心；Jia 等（2016）对FDPC 算法进行了改进，提出了增强的快速聚类算法E−FDPC（Enhanced−FDPC），该算法通过加权归一化的局部密度和组内距离来计算每个波段的排名得分；Yuan 等（2016）提出了一种基于上下文分析和双聚类的高光谱图像波段选择方法；Wang 等（2018）提出了一种用于高光谱波段选择的最佳聚类框架，该框架通过动态编程将高光谱波段划分为多个组，并在每个组中选择一个代表性波段；赵亮等（2019）提出了一种基于平均相关性和最佳指数等指标的高光谱图像子空间波段选择方法；Wang 等（2019）提出了一种用于波段子空间划分的自适应分区框架，通过最大化组间距离与组内距离之比将光谱空间中有序的高光谱数据划分为多个子空间，可以有效避免选择具有高相关性的波段子集。

上述基于聚类的高光谱图像波段选择方法主要考虑了波段的信息量和相关性，忽视了波段的噪声问题。然而受瑞利散射、水和二氧化碳吸收等大气噪声及传感器自身噪声的影响，真实的高光谱图像通常在某些波段有严重的噪声。这些噪声会对波段信息量估计和波段间相似度计算产生不利影响，甚至导致选择的波段子集中包含多个噪声波段的情况。现有的波段选择方法为避免这种情况，通常会将特定传感器中的水吸收波段等受噪声影响严重的波段去除，但在高光谱图像的成像过程中产生噪声波段的因素众多，去除特定水吸收波段后的数据集中仍然存在其它的噪声波段（刘雪松等，2012），因此在波段选择过程中考虑噪声问题是非常有必要的（Wang 等，2019）。本文提出一种噪声鲁棒的高光谱图像子空间划分与波段搜索方法，即基于皮尔逊相关系数、信息熵和 噪 声 水 平PIENL （Pearson correlation coefficient，Information Entropy and Noise Level）的波段选择方法。PIENL方法首先采用抗噪声干扰能力较强的皮尔逊相关系数计算波段间相似度，然后基于波段相似度自适应地将高光谱图像划分成有序的子空间，最后综合考虑波段的信息熵和噪声水平，在各个子空间中挑选出信息量大且噪声水平低的代表性波段。

2 方 法

本文方法首先依据波段间皮尔逊相关系数对高光谱图像进行自适应子空间划分，得到相关性较弱的多个波段子空间；然后使用结合波段信息熵和噪声水平两个指标的信息量度量准则在各个子空间中进行搜索，选择最具代表性的波段子集。

2.1 子空间划分

2.1.1 划分依据

高光谱遥感数据具有光谱划分精细的特点，同一地物在相邻波段的光谱反射率相近（赵亮等，2019）。为了将相似波段划分到同一子空间，需要衡量各个波段之间的光谱差异（Wang 等，2019）。目前波段间光谱差异的度量方法主要有距离度量（Wang 等，2019） 和相关性度量（赵春晖 等，2017；赵亮等，2019）。图1 展示了欧氏距离和皮尔逊相关系数在Indian Pines 数据集与Salinas 数据集上的可视化矩阵。

图1（a）和图1（c）分别展示了欧氏距离在Indian Pines 数据集与Salinas 数据集上的可视化矩阵。根据右侧图例，越靠近深蓝色区域欧氏距离越小，代表波段间的光谱差异越小；越靠近深红色区域欧氏距离越大，代表波段间的光谱差异越大；可以看出，噪声波段与其他正常波段间的欧氏距离较大，但噪声波段间的欧氏距离较小，例如Indian Pines 数据集中103—112 波段和148—165 波段，Salinas数据集中108—112波段和154—167波段。

皮尔逊相关系数可视化矩阵如图1（b）与图1（d）所示。皮尔逊相关系数的绝对值越大，代表波段之间的相关性越强。根据右侧图例，深蓝色区域代表波段间呈现负相关，暗红色区域代表波段间呈现正强相关，黄色区域代表波段间相关性较弱，青色及浅蓝色区域代表波段间基本不相关；可以看出，相关性较强的区域主要集中在主对角线附近，说明相邻波段间的相关性更强（赵亮等，2019），但噪声波段间基本不相关或弱相关，例如Indian Pines 数据集中103—112 波段和148—165 波段，Salinas 数据集中108—112 波段和154—167波段。

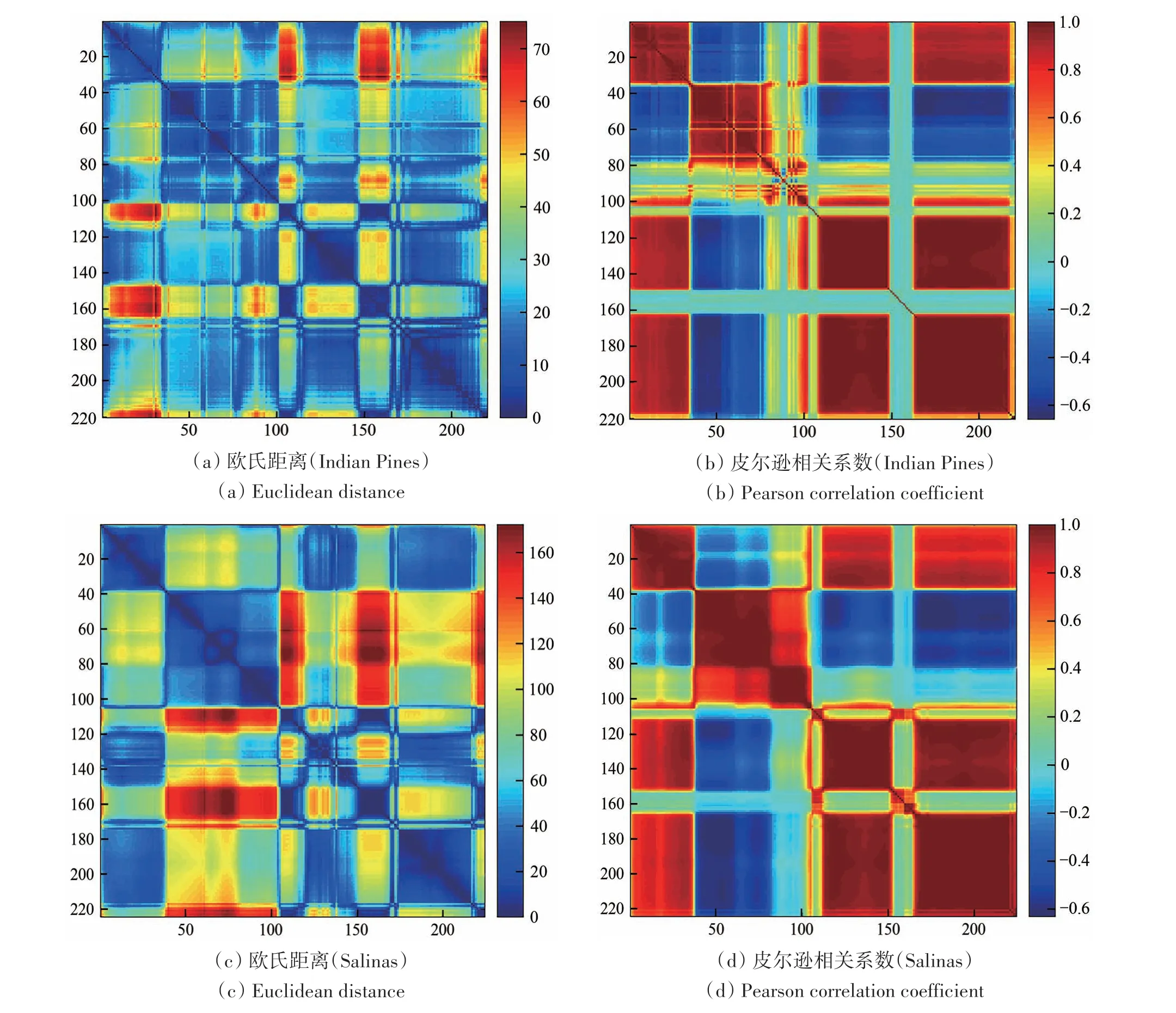
图1 欧氏距离与皮尔逊相关系数的可视化矩阵Fig.1 Visual matrix of Euclidean distance and Pearson correlation coefficient

依据欧氏距离度量波段间差异时，噪声波段与非噪声波段间的距离较大，但噪声波段之间的距离较小（例如Indian Pines 数据集中103—112 波段和148—165 波段）。因此，在采用欧氏距离划分子空间时，可能出现同一子空间中所有波段都是噪声波段的情况，致使下一阶段所选的最具代表性波段子集中必然存在噪声波段。图2 展示了在未去除噪声波段的Indian Pines 数据集上分别采用欧氏距离与皮尔逊相关系数的子空间划分情况，其中噪声波段区域使用黑白纹理标注。可以看出，采用欧氏距离的分区方法将噪声波段148—165、218—220 单独分成同一子空间。与欧氏距离不同，皮尔逊相关系数基于波段间的协方差和波段标准差计算两个波段的相似度（Algina 和Olejnik，2003），噪声波段间皮尔逊相关系数较小（例如Salinas 数据集中108—112 波段和154—167 波段），甚至接近于0 （例如Indian Pines 数据集中103—112 波段和148—165 波段），因此基于皮尔逊相关系数的子空间划分方法有助于避免将噪声波段单独分成同一子空间。据此本文选用皮尔逊相关系数作为高光谱图像子空间的划分依据。

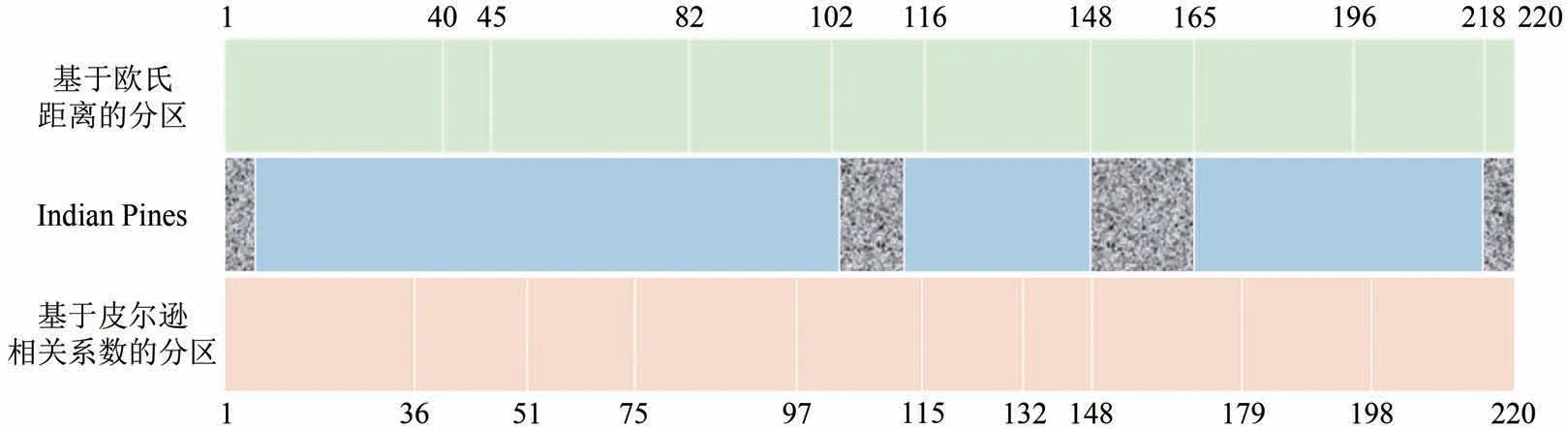
图2 在Indian Pines数据集上的分区情况Fig.2 Partition on the Indian Pines dataset

假设高光谱数据集X=[x1，x2，…，xL]，其中L代表高光谱图像的波段数。波段间皮尔逊相关系数的计算如式（1）所示：

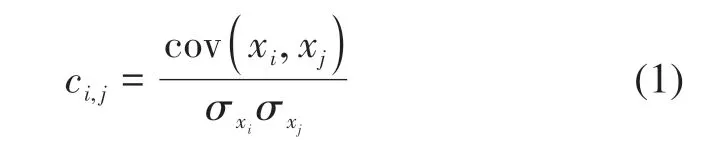
式中，cov(xi，xj)是第i个波段xi与第j个波段xj的协方差，σxi和σxj分别是xi与xj的标准差。ci，j表示第i个波段xi与第j个波段xj的皮尔逊相关系数。ci，j的绝对值越大，代表xi和xj之间的相关性越强（Zhang 等，2018）。所有波段的皮尔逊相关系数矩阵A可以表示如下

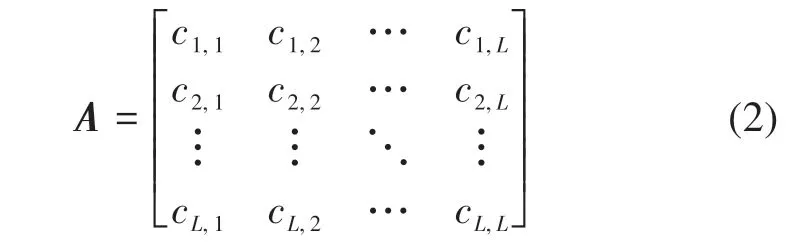
2.1.2 基于皮尔逊相关系数的自适应子空间划分

式中，Bk代表划分后的第k个子空间，|Bk|为第k个子空间的波段数。参照Wang 等（2019）提出的子空间划分方法，定义子空间划分的优化问题如下：

然而，当高光谱图像中存在噪声波段时，式（5）倾向于将连续噪声波段单独划分成一组。这是因为噪声波段组与其他波段组光谱相关性较弱，如果选择分割点tk使得所有噪声波段分为一组，则式（5）中的分子项会取得最小值，而分母项数值近似等于非噪声波段组相关性的大小，因此这种划分方法容易导致代表性波段子集中出现噪声波段。

为解决式（5）倾向于将连续噪声波段单独划分成一组的问题，本文提出使用乘积运算取代式（5）分子式中分母项的求和运算。这是因为噪声波段组内部相关性较小，相比求和运算，乘积运算会大幅降低分母项数值的大小，从而避免在噪声波段组划分为一个子空间、非噪声波段组划分为一个子空间的情况下分子式取得最小值。改写后的优化问题目标函数可表达如下：

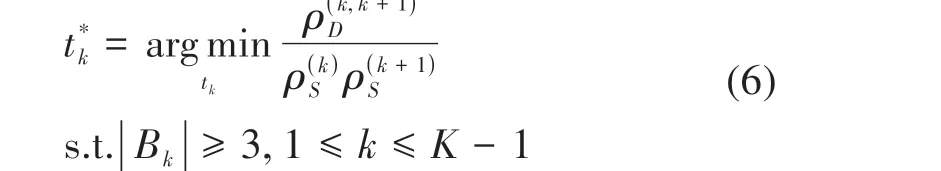
结合式（3）与式（4），式（6）可以写成：

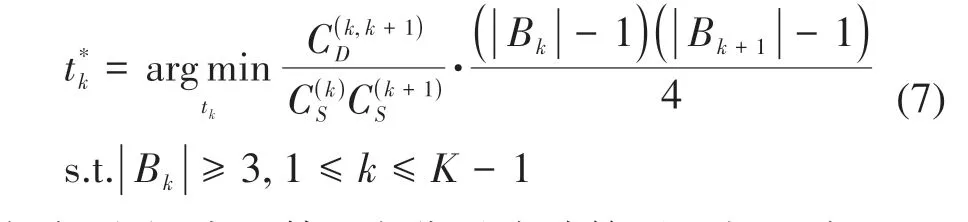
在式（7）中，第2 个分子式计算子空间Bk与Bk+1波段数量分别减1后的乘积，目标函数的优化过程将使得这两个子空间中的波段数量差别较大。这是因为当总波段数量一定时，两个子空间波段数相差越大，第2 个分子式的值越小。假设总共有10 个波段，当Bk= 2、Bk+1= 8 时，第2 个分子式的值为1.75；当Bk= 5、Bk+1= 5 时，第2 个分子式的值为4，显然最小化优化问题的目标函数将倾向于选择前一种划分策略。为了解决这一问题，依据Geoffrion（1974）和Guignard（2003）关于最小化问题的松弛定义，对式（7）中的优化问题进行了松弛处理，如式（8）所示：

通过对优化问题（7）的松弛处理，可以有效缓解各子空间波段数目不均衡的问题。据此，本文通过求解式（8）的最优化问题，得到第k个子空间与第k+ 1个子空间之间的最佳分割点。

2.2 波段搜索准则

波段搜索准则旨在从子空间中选出高光谱图像信息量大、类别可分性较好的波段组合。波段方差、信息熵和噪声水平等是常用的波段评价依据（谷延锋和张晔，2003；蒋金豹 等，2016；Zhang 等，2016；Wang 等，2019）。当高光谱图像中包含噪声时，噪声波段会对图像质量产生较大影响，增加图像分类任务的不确定性。

为了选择子空间中信息量大、且噪声水平低的波段作为该子空间的代表性波段，本文提出的波段搜索准则将通过组合信息熵和噪声水平两个指标来评估各个波段的信息量。选择子空间Bk中代表性波段yk的优化任务可以定义如下：

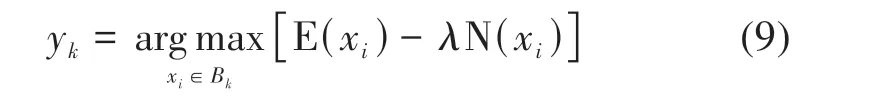
式中，E(xi)和N(xi)分别代表波段xi的信息熵和噪声水平，λN(xi)为惩罚项，λ为惩罚系数，可以通过实验选取使波段选择结果最优的λ值。波段的噪声水平计算采用Coakley 和Bretherton（1982）给出的方法。依据式（9）计算划分到子空间Bk中所有波段的信息量，将具有最高信息量的波段选为该子空间的代表性波段。子空间划分与波段搜索方法（PIENL）的实现过程为

输入：高光谱数据集X=[x1，x2，…，xL]，代表性波段数K。

3 实验与分析

3.1 实验数据

本文使用3个公开常用的高光谱数据集来验证所提出方法的有效性。

（1）Indian Pines 数据集：通过AVIRIS 传感器采集，由145像素×145像素和220个波段组成，波长范围在0.4—2.5 μm 之间，空间分辨率为20 m，包含16 种地物类型；其中，信噪比较低的波段有1—3、103—112、148—165 和217—220 等35 个波段（Zhang 等，2018）。去掉水和二氧化碳吸收严重噪声波段（104—108、150—163和220）后的修正数据集共200个波段，Indian Pines数据集假彩色图像及其真值图如图3所示。

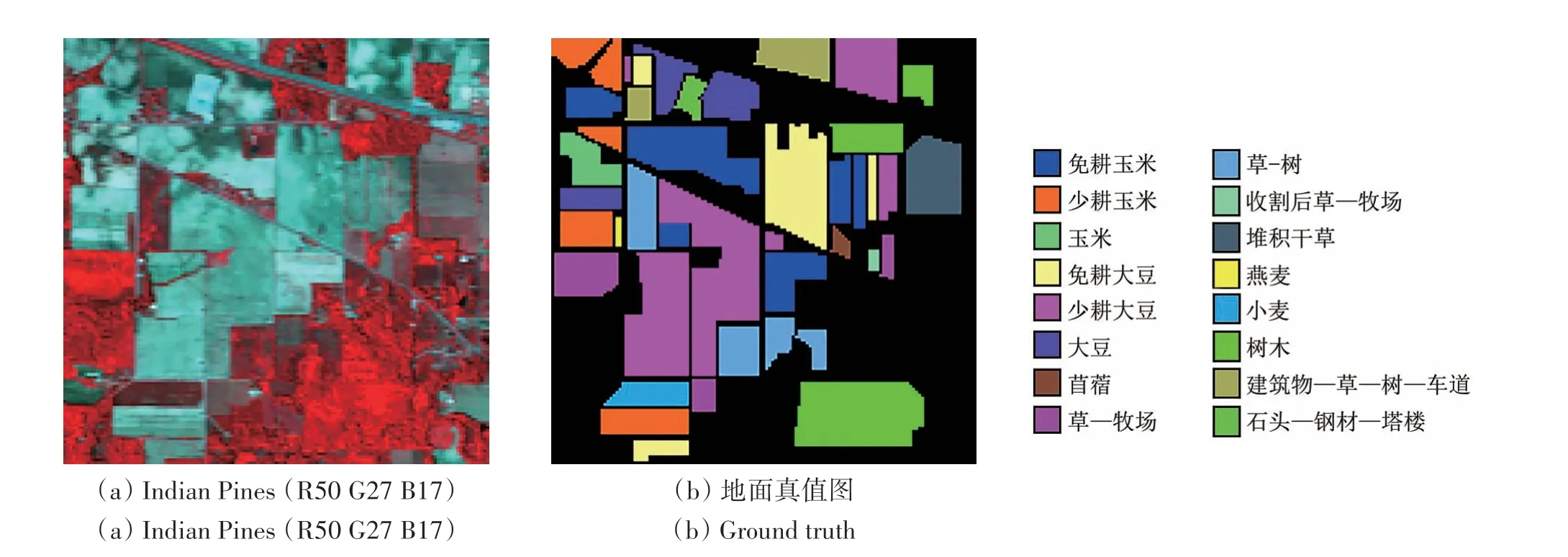
图3 Indian Pines数据集Fig.3 Indian Pines dataset

（2）Washington DC 数据集：通过HYDICE 传感器拍摄，由280×307 像素和191 个波段组成，波长范围在0.4—2.4 μm 之间，空间分辨率为1.5 m，包含6 种地物类型。由于航拍数据噪声水平较低，本文人为地对波段61—80和141—150等30个波段添加10%的高斯噪声以检验不同波段选择算法的抗噪能力，将人为添加噪声后的图像作为未去除噪声波段的数据集；Washington DC 数据集假彩色图像及其真值图如图4所示。

图4 Washington DC数据集Fig.4 Washington DC dataset

（3）Salinas 数据集：通过AVIRIS 传感器采集，由512像素×217像素和224个波段组成，空间分辨率为3.7m，包含16 种地物类型。受大气影响较大和信噪比较低的波段有108—112、154—167和224 等20 个波段，去除噪声严重波段后的修正数据集共204个波段；Salinas数据集假彩色图像及其真值图如图5所示。

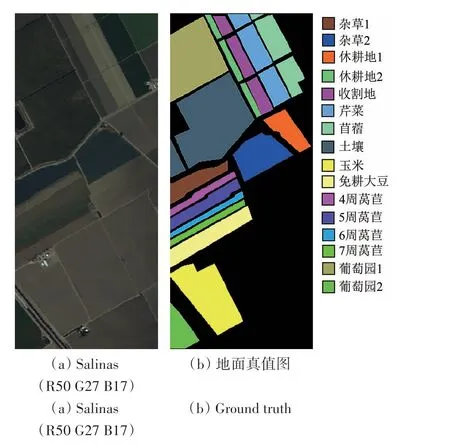
图5 Salinas数据集Fig.5 Salinas dataset

3.2 评价指标

本文通过波段平均相关性与分类精度两种指标来验证所提出方法的有效性，并分析各种波段选择方法的噪声鲁棒性。

（1）分类精度：总体精度（OA）、平均精度（AA）和Kappa 系数用于量化分类效果。在实验中使用SVM 分类器对高光谱图像进行分类，并采用径向基函数作为核函数。通过交叉验证方法估计最优方差参数和惩罚因子。每次实验随机选择10%的样本进行训练，其余样本用于测试。分类精度采用10次独立运行实验精度的平均值和标准差。

（2）波段相关性：本文使用波段平均相关系数（ACC）评估所选的代表性波段的相关性，ACC的绝对值越大，波段平均相关性越强，冗余度越高。

（3）噪声鲁棒性：以Indian Pines和Salinas数据集为例，对不同方法所选择的代表性波段进行分析和比较，评价各种波段选择方法对噪声的鲁棒性。

3.3 参数设置

在计算波段噪声水平时，需要事先将每个波段图像划分为M×M像素大小的小块（Coakley 和Bretherton，1982）。Wang 等（2019）详细分析了块大小对不同数据集的影响。参考Wang等（2019）论文中的实验结果数据，本文在Indian Pines 数据集上取M= 3，在Washington DC数据集上取M= 5，在Salinas数据集上取M= 10。

在式（9）的目标函数中，参数λ的最优值通过实验确定。图6给出了在3个数据集上选取10个代表性波段时，随着λ值逐步增加，分类精度的变化情况。本文在Indian Pines 和Washington DC 数据集上取λ= 100，在Salinas数据集上取λ= 125。

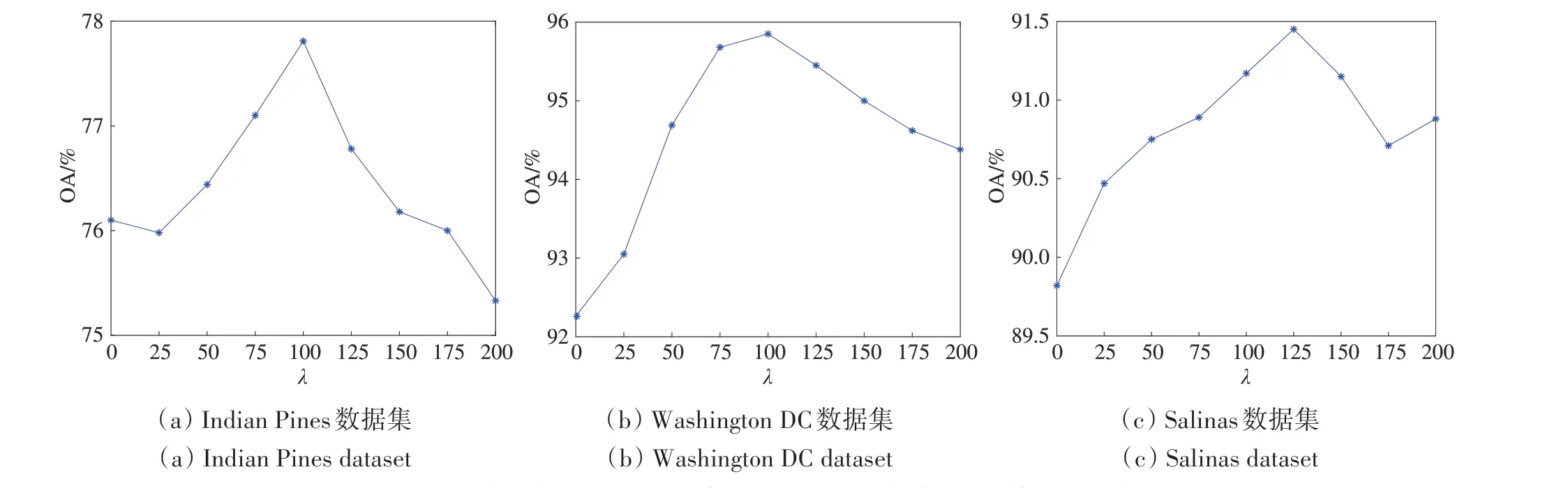
图6 在3个数据集上选取10个代表性波段的分类精度随λ值的变化曲线Fig.6 Classification accuracy of 10 representative bands selected from three datasets varies with the value of λ

3.4 实验结果与分析

实验环境为Intel Core i7−6700四核处理器，主频3.40 GHz，有效内存32 GB，开发环境为Matlab R2017b。本文将PIENL方法与Chang等（1999）提出的最大方差主成分分析方法MVPCA（Maximum−Variance PCA），Chang 和Wang （2006）提出的基于线性约束最小方差的波段相关最小化方法LCMVBCM （Linearly Constrained Minimum Variance based Band Correlation Minimization）， Martínez−Usómartinez−Uso 等（2007）提出的沃德发散联动策略（WaluDI），Rodriguez 和Laio（2014）提出的基于快速密度峰的聚类算法（FDPC）和Wang 等（2019） 提出的自适应子空间噪声最小化方法（ASPS_MN）等波段选择方法进行了对比实验。其中，ASPS_MN 方法在波段搜索阶段同样考虑了噪声的影响，该方法将Coakley 和Bretherton（1982）提出的噪声水平计算方法作为波段搜索准则。为了充分验证本文提出方法的优越性，在去除噪声严重波段的修正数据集与未去除噪声波段的数据集上均进行了对比实验。

3.4.1 基于皮尔逊相关系数的自适应子空间划分有效性验证

（1）子空间划分的目标函数有效性验证。以Indian Pines 高光谱图像的148—197 波段（共50 个连续波段，其中148—165 为噪声波段，166—197为非噪声波段）为实验数据集，验证式（8）中目标函数的有效性，实验结果如图7 所示。由图7 可以看出，在所有可能划分情况下，式（5）中的目标函数在将连续噪声波段148—165 划分为一个子空间、非噪声波段166—197 划分为另一个子空间时取得最小值；式（6）和（7）中的目标函数在分割点为194时取得最小值，避免了将连续噪声波段148—165 划分为一个子空间的情况，然而两个子空间中的波段数量分别为47 和3，相差极大；式（8）中的目标函数在分割点为179 时取得最小值，既避免了相邻子空间Bk与Bk+1中波段数量不均衡的问题，也避免了将连续噪声波段单独划分为一个子空间的情况。因此，选用式（8）作为自适应子空间划分优化问题的目标函数是有效的。

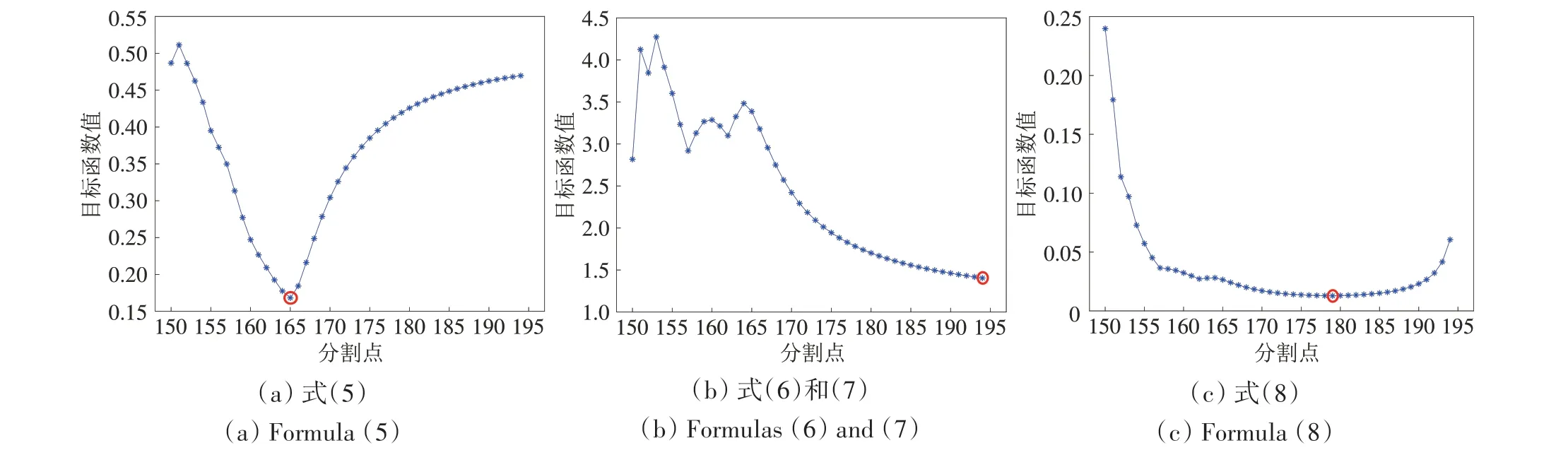
图7 不同目标函数对最佳分割点选择的影响（红圈代表最佳分割点）Fig.7 Adjacent subspace partition points of different objective functions（the red circle represents the best partition point）

（2）与其他子空间划分方法的对比实验。为了验证本文提出的基于皮尔逊相关系数的子空间划分方法的有效性，本文将PIENL 方法与其他子空间划分方法及波段均分方法进行了对比。其中，增强的快速聚类算法E−FDPC（Jia 等，2016）和波段均分方法（根据所选代表性波段的数量将高光谱数据集平均划分） 为非自适应划分方法，ASPS_MN 和PIENL 为自适应子空间划分方法。表1展示了在3个数据集上选取20个代表性波段时的分类精度。为了消除子空间波段搜索方法差异的影响，对比方法在波段搜索过程中均使用本文提出的子空间波段搜索方法，在表1中使用*标注。从表2 中可以看出，PIENL 方法在去除噪声严重波段的修正数据集上总体精度比ASPS_MN 方法提高了大约1%，比E−FDPC 方法及波段均分方法提高了大约1%—2%，Kappa 系数在3 个修正数据集上提高了1%—5%左右。PIENL 方法在未去除噪声波段数据集上总体精度比ASPS_MN 方法提高了大约1%—3%，比E−FDPC 方法及波段均分方法提高了大约1%—2%，Kappa 系数提高了大约1%—5%。在几种对比方法中，PIENL的分类精度最高，证实了本文提出的基于皮尔逊相关系数的子空间划分方法的有效性。

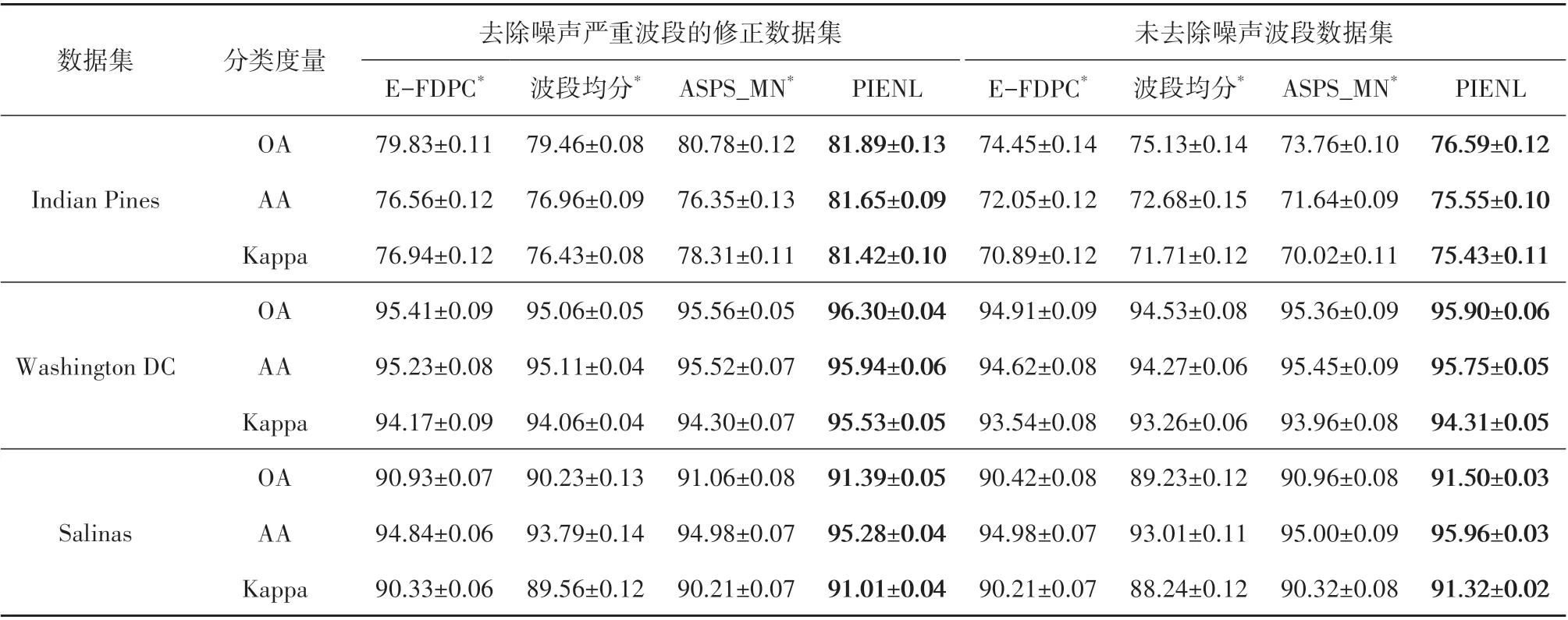
表1 在3个数据集上分别选取20个代表性波段用于验证子空间划分方法的有效性Table 1 Select 20 bands to verify the effectiveness of the subspace partition method on three hyperspectral datasets/%

3.4.2 提出的波段信息量度量方法有效性验证

为了验证本文提出的波段信息量度量方法的有效性，本文在3个未去除噪声波段的数据集上采用相同的子空间划分方法验证不同度量方法选取代表性波段的类别可分性。图8 展示了在3 个未去除噪声波段数据集上，使用不同度量方法选取不同数量代表性波段时的OA 曲线。从图8 中可以看出，采用本文提出的信息量度量方法选取的代表性波段的OA 明显高于使用方差、信息熵和噪声水平作为波段搜索准则的方法，这也证实了采用本文在波段搜索阶段改进的信息熵与噪声水平相结合的信息量度量方法可以选出子空间中信息量大且噪声水平低的代表性波段，具有较好的类别可分性。

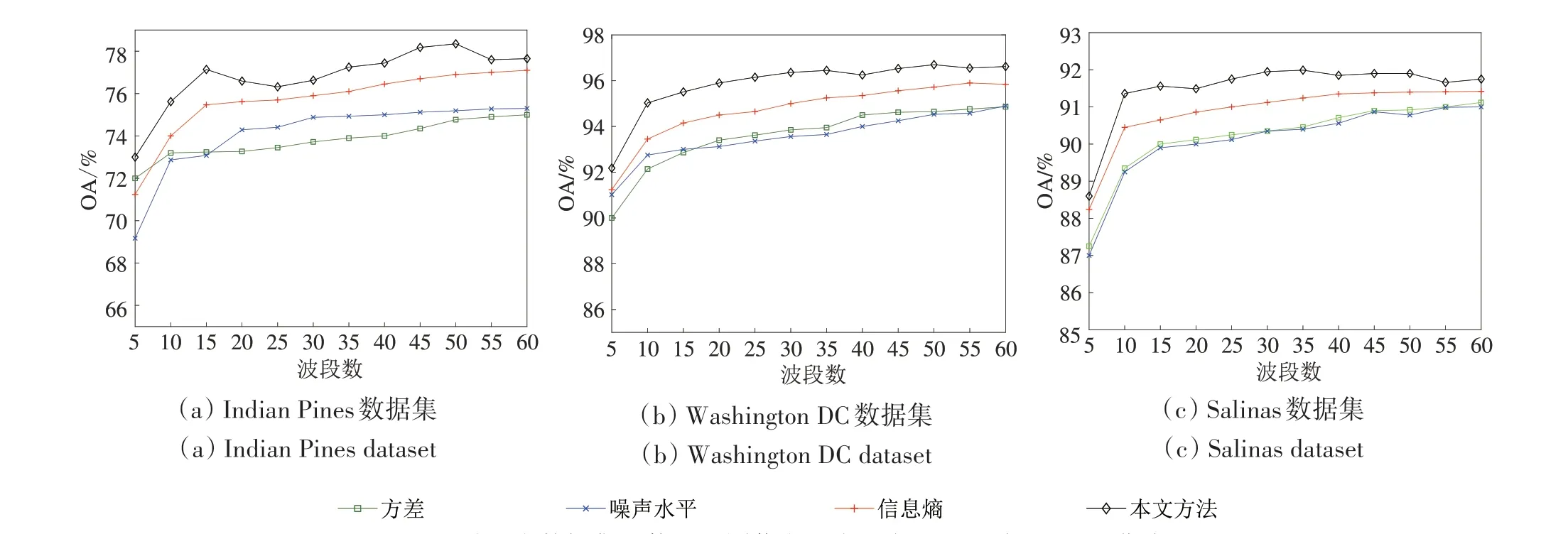
图8 在3个数据集上使用不同信息量度量方法选取波段的OA曲线Fig.8 OA for using different information measurement methods to select bands on three datasets

3.4.3 修正数据集上的结果与分析

（1）类别可分性。图9展示了几种波段选择方法在3个去除噪声严重波段的修正数据集上选取不同数量代表性波段的OA 变化曲线。从总体变化趋势上看，大部分方法的分类精度随所选代表性波段数量的增加而增加。当所选波段达到30 个以上时，各种方法的精度基本趋于稳定。图9中水平虚线为使用全波段分类的结果。PIENL 方法在3 个修正数据集上选择20—30 个代表性波段时，精度达到或超过使用全波段分类的结果。从图9（a）可以看出，当PIENL 方法在Indian Pines 数据集上选择代表性波段的数量超过15个时，其分类精度明显高于其他方法。各种波段选择方法在Washington DC 和Salinas 数据集上的分类精度变化曲线分别由图9（b）和图9（c）给出。与Indian Pines 数据集相比，PIENL 方法在Washington DC 和Salinas 数据集上的优势并不明显，这是由于Indian Pines 数据集是由星载传感器拍摄，受大气噪声影响较为严重，波段的噪声水平较高，而Washington DC 和Salinas 数据集是由机载传感器拍摄，空间分辨率较高，波段的噪声水平较低。

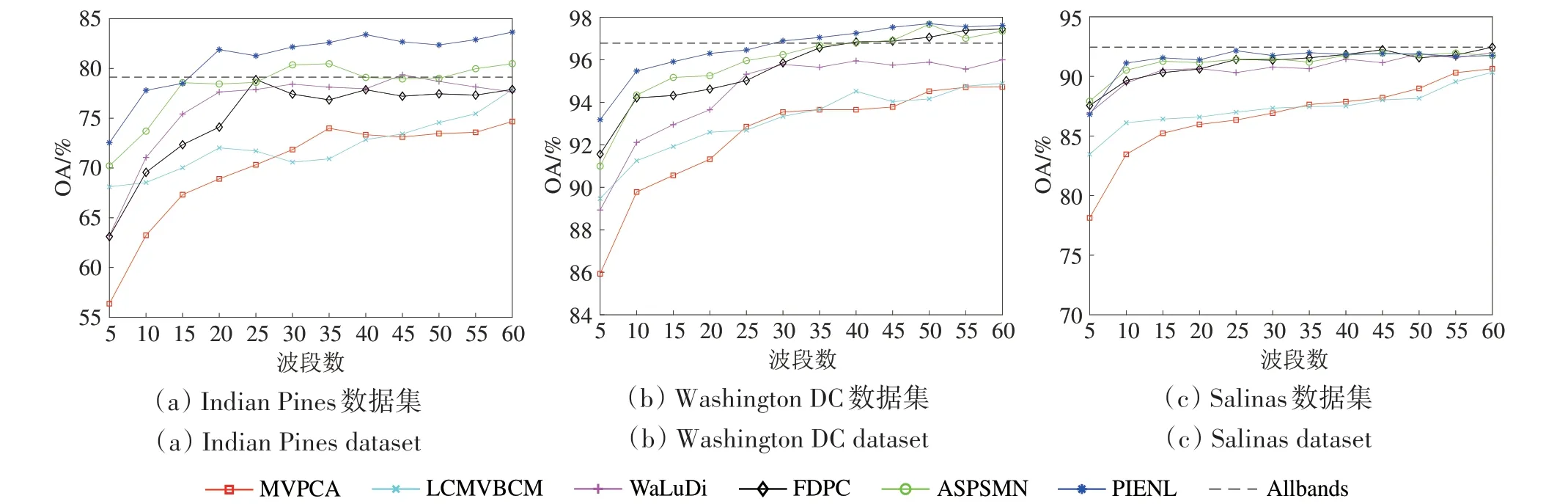
图9 在去除噪声严重波段的修正数据集上选取不同数量波段的OA曲线Fig.9 OA for selecting different numbers of bands on the dataset with high−noise bands removed

表2给出了在3个修正数据集上分别选取10个代表性波段的总体精度（OA）、平均精度（AA）和Kappa系数。当选取10个代表性波段时，PIENL方法与ASPS_MN 方法在去除噪声严重波段的Indian Pines 数据集上明显优于其它方法，可以说明在去除噪声严重波段后的数据集上考虑噪声影响也是十分必要的。从表2中可以看出，本文提出的PIENL 方法在各个数据集上都取得了较好的结果。PIENL 方法在的Indian Pines 数据集上总体精度相比其它方法提高了3%—13%，分类精度已经非常接近使用所有波段分类的结果，在Washington DC 数据集上总体精度相比其它方法提高了1.5%—6.0%，在Salinas 数据集上总体精度相比其它方法提高了1%—6%。

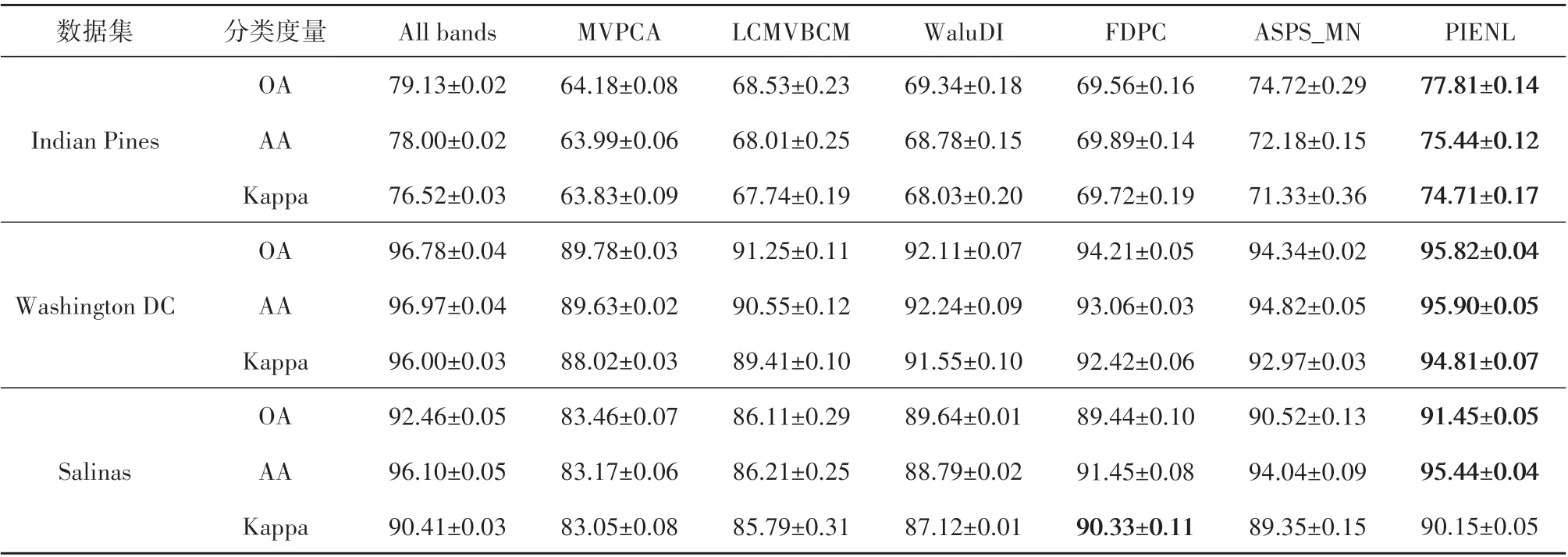
表2 在3种修正数据集上选取10个代表性波段的分类精度Table 2 Classification accuracy of 10 representative bands selected on three datasets with high-noise bands removed/%

PIENL方法在去除噪声严重波段后的修正数据集上效果仍然优异的原因如下：一是提出的基于皮尔逊相关系数的子空间划分方法能够降低代表性波段间的相关性，从而减少所选波段之间的冗余信息；二是修正数据集中仍包含部分信噪比较低的波段，噪声增加了高光谱图像分类任务的不确定性，在波段搜索过程中提出改进的波段信息量度量方法能够同时兼顾信息熵和噪声水平，选出子空间中信息量大且噪声水平低的波段。在3个数据集上选取10 个代表性波段的分类图由图10、图11和图12给出。

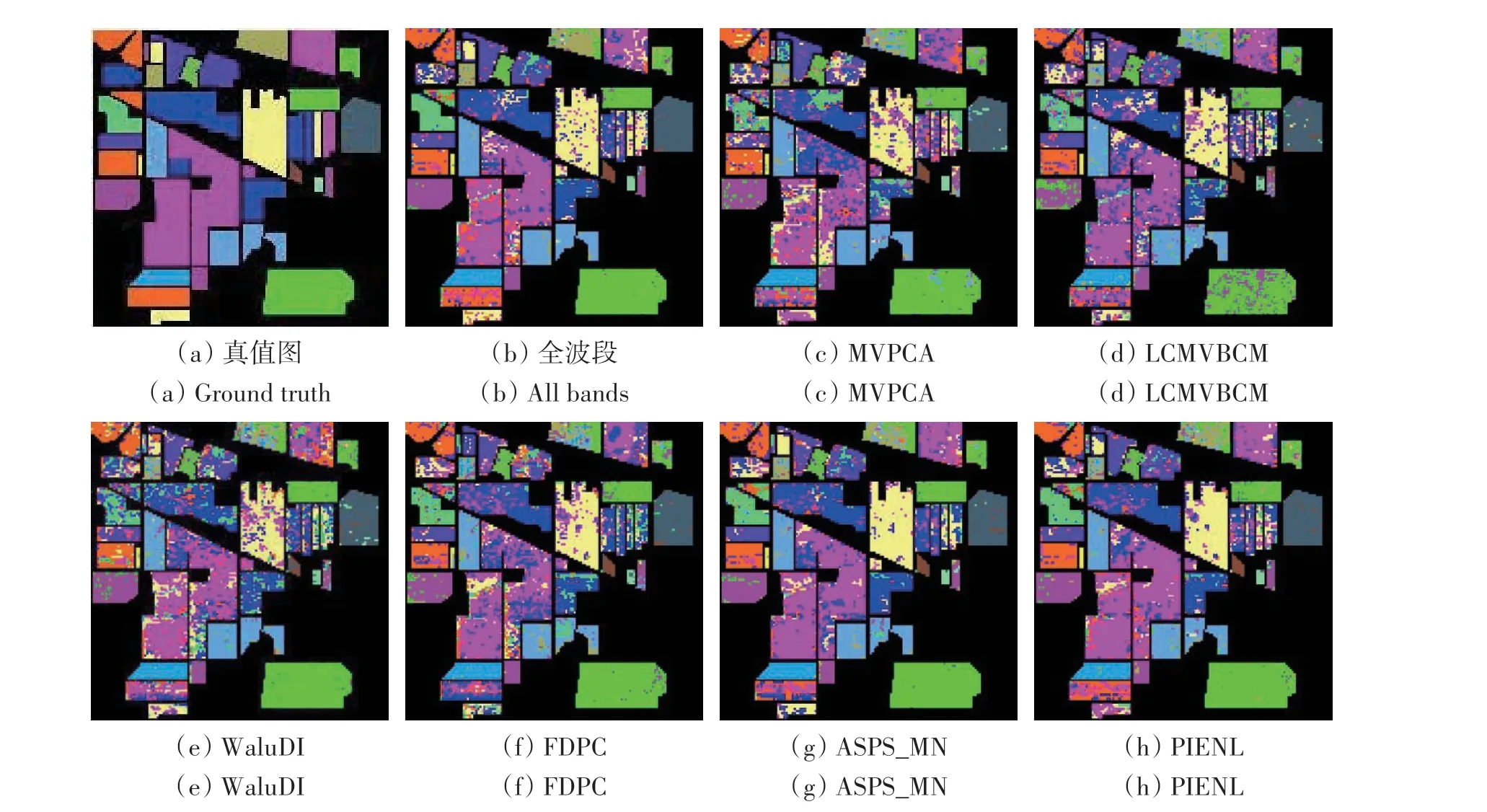
图10 不同方法的Indian Pines图像分类结果Fig.10 Indian Pines image classification results obtained by different methods

图11 不同方法的Washington DC图像分类结果Fig.11 Washington DC image classification results obtained by different methods

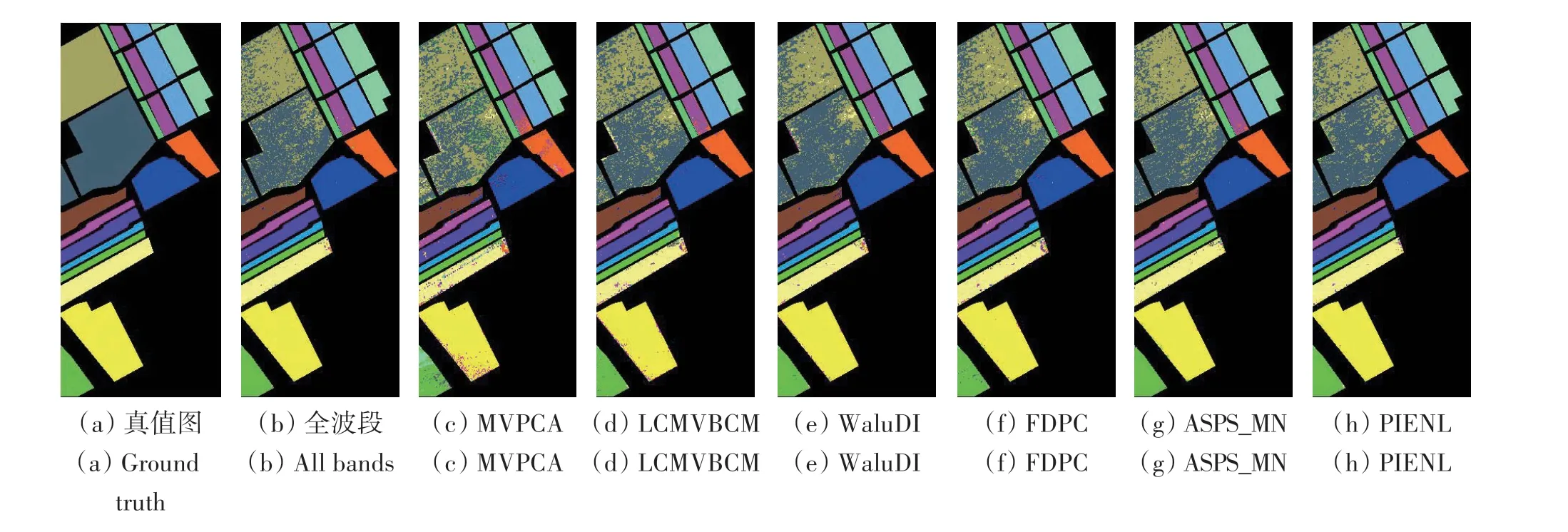
图12 不同方法的Salinas图像分类结果Fig.12 Salinas image classification results obtained by different methods

（2）相关性分析。表4 展示了在3 个数据集上分别选取10 个代表性波段的平均相关系数。对于高光谱数据，代表性波段的平均相关性越小，波段子集冗余度越低。平均相关系数ACC 的取值范围为［−1，1］：|ACC|<0.2 为极弱相关或不相关；0.2≤|ACC|<0.4 为弱相关；0.4≤|ACC|<0.6 为中等程度相关；0.6≤|ACC|<0.8 为强相关；0.8≤|ACC|≤1 为极强相关（Acito 等，2011）。在Indian Pines 数据集上，PIENL 及ASPS_MN 方法选取波段子集的ACC 相比其它方法是较低的，其值都小于0.4，即它们选择的代表性波段之间为弱相关，而其他方法选择的代表性波段之间为中等程度相关甚至强相关。在Washington DC 和Salinas 数据集上，PIENL方法较其他方法的ACC 是最低的。在Salinas 数据集上，PIENL 方法所选波段子集的ACC 只有0.2 左右，说明代表性波段的冗余度非常低。

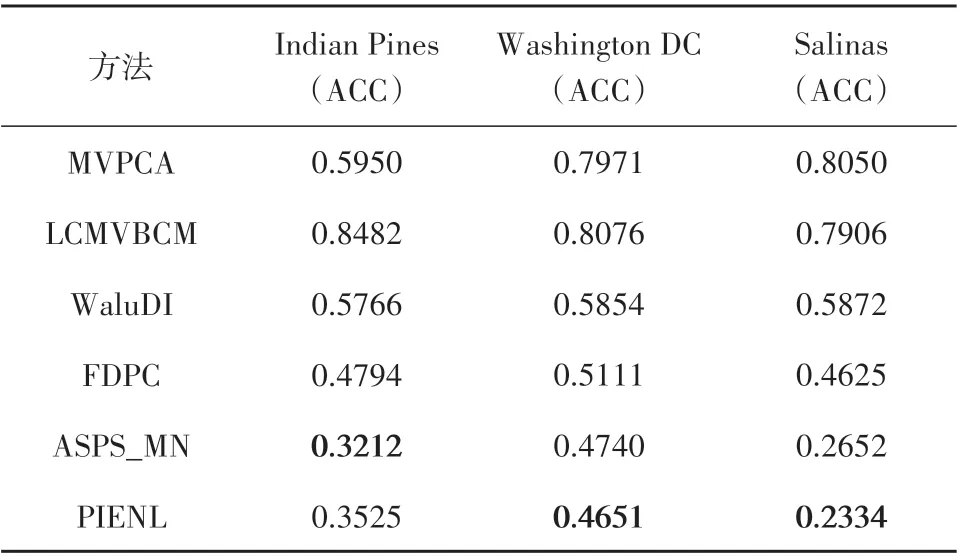
表4 3个数据集上选取10个代表性波段的平均相关系数Table 4 Average correlation coefficient of 10 representative bands selected on three datasets

3.4.4 未去除噪声波段数据集上的结果与分析

（1）类别可分性。图13 展示了几种波段选择方法在3 个未去除噪声波段的高光谱数据集上的OA 变化曲线。从总体变化趋势上看，大部分方法的分类精度随所选代表性波段数量的增加而增加。图13 中水平虚线代表使用全波段分类的结果，与图9中水平虚线相比，使用未去除噪声波段的全波段进行分类时，分类精度明显降低。从图13 中可以看出，当仅选择10 个代表性波段时，PIENL 方法的精度便达到或高于使用全波段进行分类的精度。ASPS_MN 等波段选择方法受噪声影响较大，而PIENL 方法在3个未去除噪声波段的数据集上均有良好表现，证实了PIENL 方法对噪声具有较强的鲁棒性。

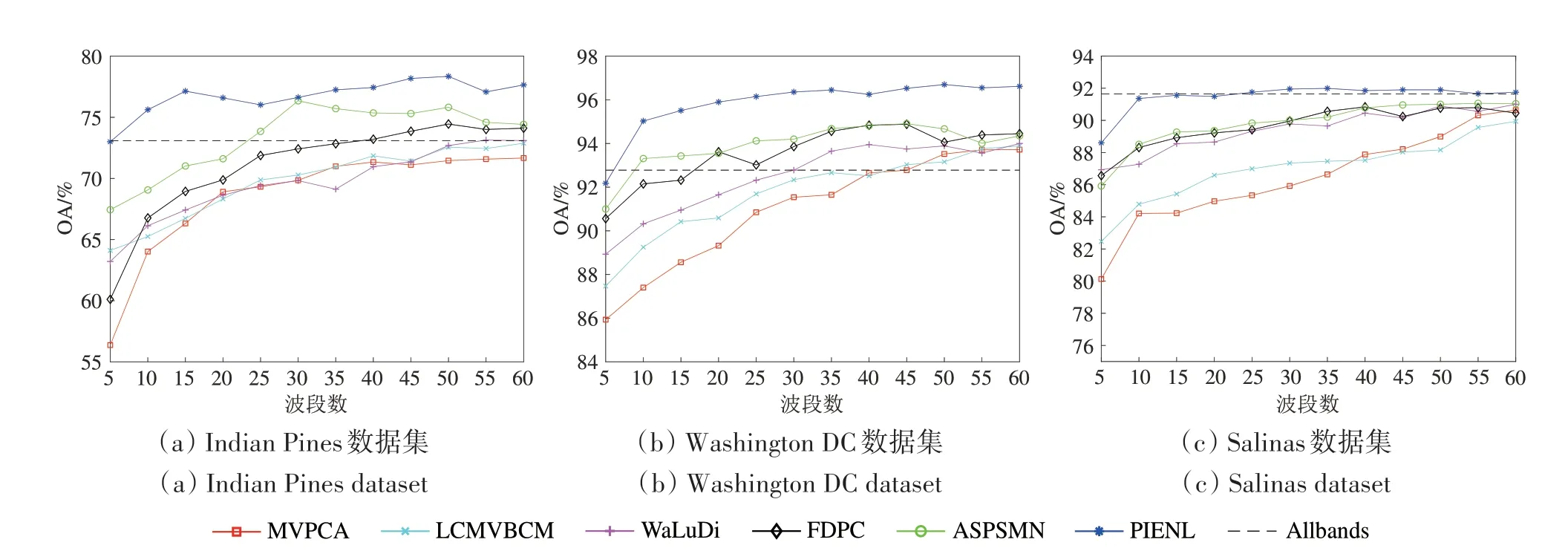
图13 在未去除噪声波段的数据集上选取不同数量波段的OA曲线Fig.13 OA for selecting different numbers of bands on datasets containing noise bands

表5 给出了在3 个未去除噪声波段的数据集上分别选取10 个代表性波段的总体精度（OA）、平均精度（AA）和Kappa 系数，从中可以看出，本文提出的PIENL 方法在各个数据集上都取得了较好的结果。在未去除噪声波段的Indian Pines 和Washington DC 数据集上选取10 个波段的分类结果高于使用所有波段及其它方法的分类精度。从表5 中可以看出，PIENL 方法在3 个未去除噪声波段的数据集上的分类精度高于其它所有方法，在未去除噪声波段的Indian Pines 数据集上相比其它方法总体精度提高了6%—11%，在Washington DC数据集上总体精度提高了2%—8%，在Salinas 数据集上总体精度提高了3%—7%，证实了PIENL方法在未去除噪声波段的数据集上表现更加优异。

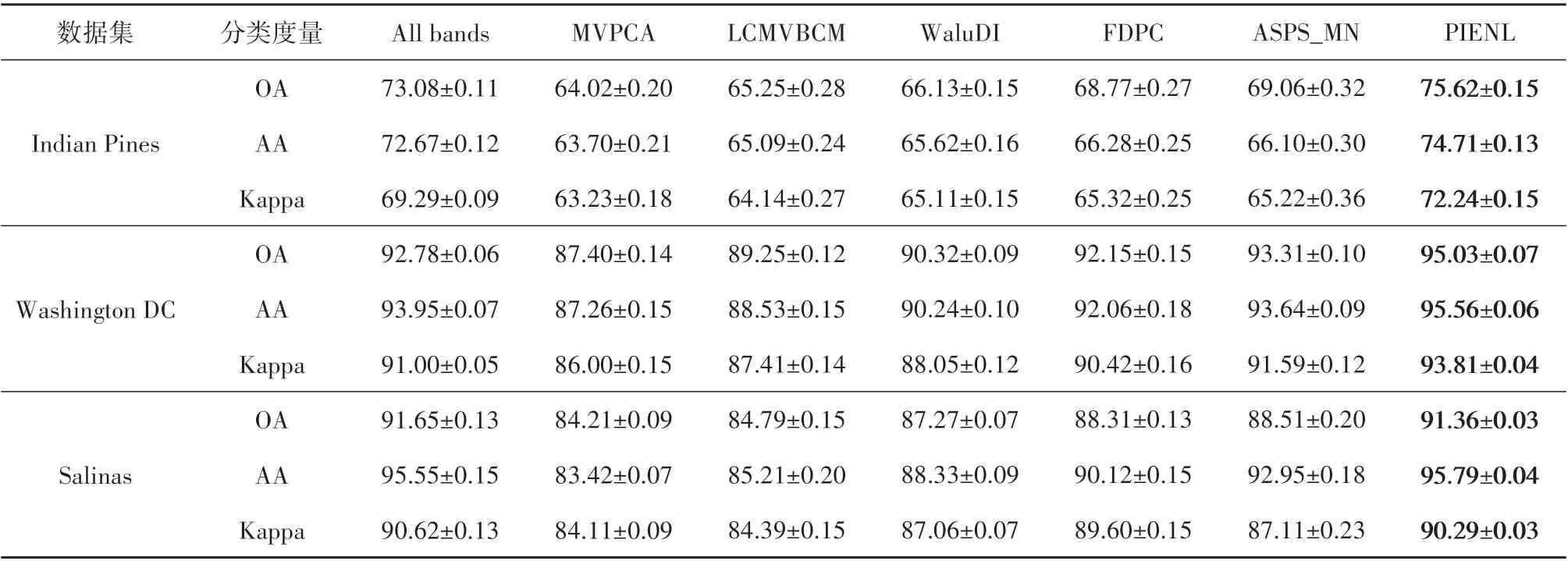
表5 在未去除噪声波段的数据集上选取10个代表性波段的分类精度Table 5 Classification accuracy of 10 representative bands selected on datasets containing noise bands/%

（2）噪声鲁棒性分析。表6 和表7 展示了不同波段选择方法在未去除噪声波段的Indian Pines 和Salinas 数据集上所选的10 个代表性波段的序号，并对其中的噪声波段进行了颜色加深标记。在未经噪声波段去除的Indian Pines 数据集上，LCMVBCM 和WaluDI 方法所选的10 个代表性波段中包含3 个噪声波段，FDPC 和ASPS_MN 方法包含了2个噪声波段。在未去除噪声波段的Salinas数据集上，LCMVBCM 和ASPS_MN 方法选择了2 个噪声波段，FDPC 和WaluDI 方法选择了1 个噪声波段。MVPCA 和PIENL 方法在两个数据集上都没有选择噪声波段作为代表性波段。然而从表6 和表7中可以看出，MVPCA 方法选择的大多数代表性波段序号都是相邻的，波段子集的信息冗余度非常高，多样性无法保证，因而相比其他方法，该方法的分类精度是最低的。PIENL方法能有效避开噪声波段，且其选择的代表性波段之间相关性较弱，因而分类精度是所有方法中最高的，这表明PIENL方法具有噪声鲁棒性。

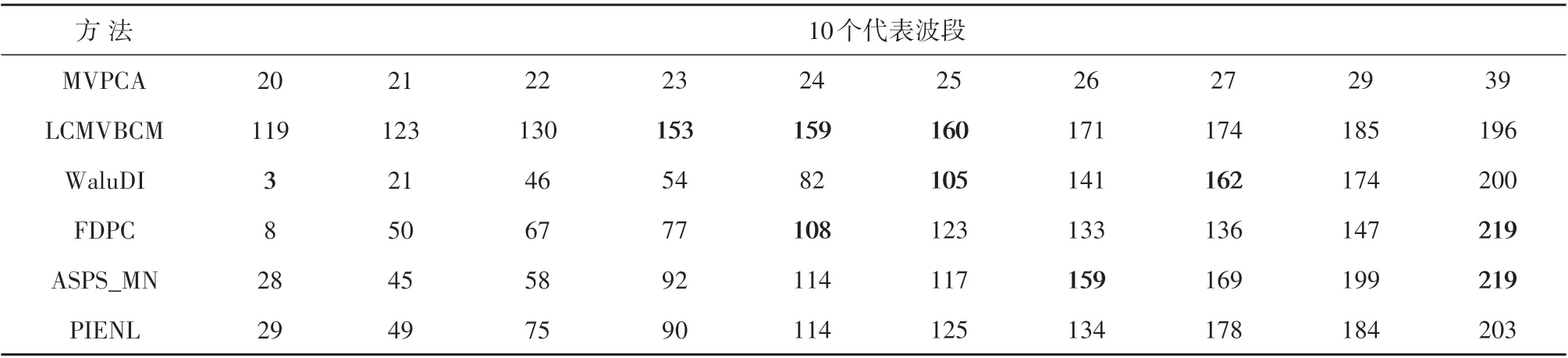
表6 不同方法在Indian Pines数据集上选取的10个波段时噪声波段包含情况Table 6 Noise bands in 10 bands selected by different methods on the Indian Pines dataset

表7 不同方法在Salinas数据集上选取的10个波段时噪声波段包含情况Table 7 Noise bands in 10 bands selected by different methods on the Salinas dataset

3.4.5 计算时间分析

表8 展示了在Indian Pines 数据集上使用不同波段选择方法分别选取10、20、30、40、50 和60 个代表性波段（k）的计算时间。可以看出，PIENL 方法的计算时间仅次于MVPCA 方法，优于ASPS_MN等其他波段选择方法。但MVPCA方法所选的代表性波段分类精度较低（图9、表3、图13和表5），而PIENL 方法所选的代表性波段在各种波段选择方法中分类精度最高。

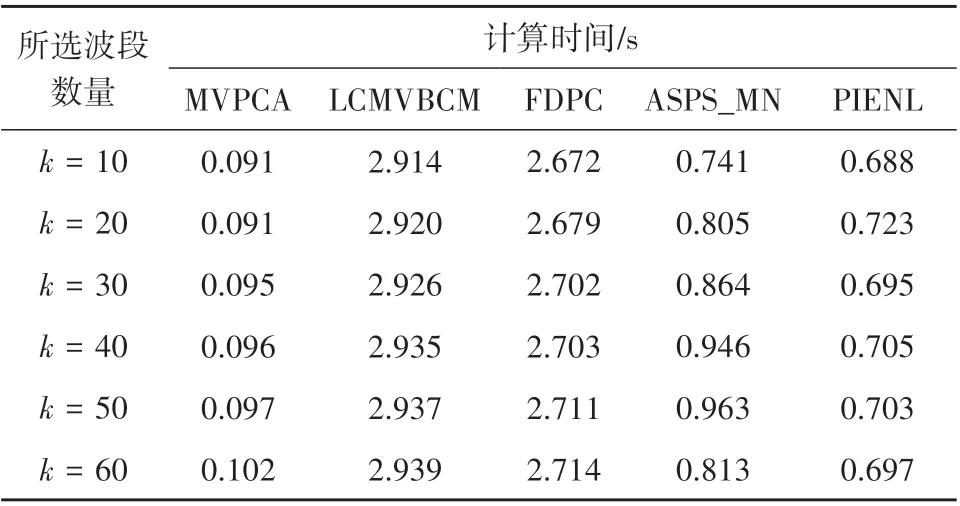
表8 在Indian Pines数据集上使用不同波段选择方法的计算时间Table 8 Computing times of different band selection methods used on the Indian Pines dataset

3.4.6 消融实验

PIENL方法在Wang等（2019）提出的ASPS_MN方法的基础上做了两点改进：一是提出基于皮尔逊相关系数的自适应子空间划分方法；二是提出基于信息熵与噪声水平的波段搜索准则。表9 在3 个数据集上分别展示了本文提出的自适应子空间划分方法及波段搜索准则的有效性。从表9中的可以看出，ASPS_MN 方法在去除噪声严重波段的修正Indian Pines 数据集上，采用本文提出的子空间划分方法的总体精度提高了2%左右，在未去除噪声的波段Indian Pines数据集上提高了3%左右，这是由于本文提出的子空间划分方法能够避免将连续的噪声波段单独划分成一个子空间，在Salinas和Washington DC 数据集上也取得了不同程度的提升，证实了本文提出的子空间划分方法的有效性和必要性。ASPS_MN 方法在未去除噪声波段的3 个数据集上使用本文提出的波段搜索准则，其总体精度提高了2%左右，证实了本文提出的使用信息熵与噪声水平相结合的波段搜索准则优于单独使用噪声水平的波段搜索准则。将基于皮尔逊相关系数的子空间划分方法及波段搜索准则相结合时，PIENL方法在未去除噪声波段的Indian Pines数据集上总体精度提高了6%以上。在Salinas和Washington DC数据集上的实验也可以得到类似结论。

4 结 论

本文针对高光谱图像波段选择结果受噪声影响较大的问题，提出了一种噪声鲁棒的高光谱图像自适应子空间划分与波段搜索方法PIENL，该方法在子空间划分和波段搜索过程中都考虑了噪声对波段选择的影响。在子空间划分阶段，使用皮尔逊相关系数度量含有噪声的高光谱图像波段间的相关性；在波段搜索阶段，提出了引入噪声水平作为惩罚项，即挑选出信息量大且噪声水平低的波段作为代表性波段。在Indian Pines、Washington DC 和Salinas 这3 个高光谱公共数据集上的实验结果表明：

（1）采用欧氏距离划分子空间时可能出现同一子空间中所有波段都是噪声波段的情况，导致下一阶段所选的最具代表性波段子集中必然存在噪声波段；而基于皮尔逊相关系数的子空间划分方法则有助于避免将噪声波段单独分成同一子空间，因此，皮尔逊相关系数更适合于度量含有噪声的高光谱图像波段之间的光谱差异；

（2）综合考虑信息熵和噪声水平两个指标度量波段信息量，有助于选出高光谱图像中信息量大且噪声水平低的代表性波段；

（3）PIENL方法选择的代表性波段具有更好的类别可分性。相比ASPS_MN 等先进的波段选择方法，PIENL 方法在3 个修正数据集上的总体精度分别提高了3%—13%、1.5%—6.0%和1%—6%；在3 个未去除噪声波段的数据集上总体精度分别提高了6%—11%、2%—8% 和3%—7%。这也表明PIENL方法在未去除噪声波段的数据集上表现更加优异。

下一步工作主要考虑PIENL 方法在子空间划分过程中自适应确定子空间的数量，避免代表性波段数量选择不当造成高光谱图像重要光谱特征缺失或波段信息冗余等问题。