考虑功率限值管理的光储系统建模及控制策略

2022-12-15刘海涛马丙泰郝思鹏张埕瑜

电力系统及其自动化学报 2022年11期

刘海涛，马丙泰，郝思鹏，陆恒，张埕瑜

（1.南京工程学院电力工程学院，南京 211167；2.江苏省配电网智能技术与装备协同创新中心，南京 211167）

随着煤、石油等能源危机与环境恶化，新能源发电技术以其无污染、可永续利用的特点受到广泛关注。由于新能源输出功率的间歇性与不稳定性，系统会出现间断性波动[1]。光伏发电的波动性和随机性会造成高渗透率光伏发电系统输出功率随机波动，进而加重了电网调节负担[2]。储能技术的发展可以很好地解决新能源发电对系统带来的影响。文献[3]对储能技术融合分布式电源的未来发展进行评估，将储能系统引入光伏发电系统能够很好地平抑光伏系统的功率波动。常见的储能器件按照功能可分为功率型和能量型器件，其中前者功率密度大，响应速度快，但能量密度小，只适用于平抑瞬时功率波动，其代表性器件有超级电容；而后者能量密度大，但动态响应能力差，循环次数有限，适用于平滑长时间的平均功率波动，其常见的有电池类储能[4]。考虑各类储能自身特性，通常将能量型与功率型储能联合使用，混合储能系统HESS（hybrid energy storage system）是将该两种类型储能通过一定的方式进行组合，从而提高储能的使用寿命。

为提升新能源输出功率效率，相关学者提出了许多功率跟踪方法，如扰动观察法、电导增量法及智能算法等。文献[5-6]为提升新能源发电利用效率，采用改进的最大功率点跟踪MPPT（maximum power point tracking）控制方法；文献[7]提出一种基于Z源逆变器的粒子群和模糊变步长电导增量MPPT算法，不仅使得最大功率点跟踪过程用时短，还可保证最大功率点追踪的稳态精度；文献[8]针对光伏发电系统MPPT精度低、速度慢的问题，提出了一种改进的基于线性自扰动电压闭环控制的变步长MPPT控制策略；文献[9-10]采用改进型变步长电导增量法进行最大功率跟踪。

针对传统比例-积分PI（proportional integral）控制存在控制稳定速度慢、系统母线电压容易产生较大超调等的问题，文献[11-13]分别提出了非线性解耦与基于深度强化学习的直流电压控制等改进控制方法，结果表明，相对于传统PI控制，改进方法能够提高直流电压的控制精度、减小扰动下直流电压波动；文献[14]考虑到常规PI内环控制无法获得理想的电压动态响应问题，提出一种抑制电压波动的双向AC/DC换流器改进内环控制策略；通过构建模糊控制规则，利用模糊逻辑控制器调节锂离子动力电池和超级电容的充放电功率，避免了高频电流波动对动力电池寿命的影响[15]。

针对混合储能能量管理控制系统，文献[16]为有效增强直流微网安全性、稳定性及其经济运行能力，基于模型预测控制理论，提出了一种直流微网HESS优化控制策略；文献[17]对混合储能电池实行分组管理，根据不同工况进行补偿预测误差的初级控制和平抑波动次级控制，能够有效解决混合储能系统过充过放问题，延长储能使用寿命；文献[18]根据蓄电池和超级电容的出力需求，结合储能设备荷电状态SOC（state of charge）等约束条件，提出混合储能系统能量管理协调控制算法，实现储能系统内部功率相互流动，保证混合储能合理运行；文献[19]通过二阶低通滤波环节对系统功率波动进行分配，并结合储能元件的SOC来控制各储能单元变换器的工作状态，进一步促进混合储能功率合理分配；文献[20]针对混合储能在新能源平抑中的配置问题，提出了一种基于元模型优化算法的混合储能双层优化配置方法，并指出蓄电池寿命主要与放电深度和充放电电流有关，该优化配置方法能够有效避免蓄电池频繁充放电，从而提高设备使用寿命。蓄电池作为能量型储能元件，充放电电流大小及波动性对自身寿命会产生较大的影响。高功率充电会导致蓄电池出现严重而明显的发热问题，电池性能维护已成为热点研究内容[21]；频繁地大功率充放电会严重影响蓄电池的使用寿命[15，22]，因此对于蓄电池承担剩余波动功率中高频功率分量进行限制具有重要意义。

基于上述分析，考虑到扰动观察法计算简单而跟踪效率差，智能算法原理较复杂且运行成本大，电导增量法中选取步长较大或较小时会产生波动或降低跟踪速度等问题，故提出一种改进新型变步长电导增量法来减少功率波动引起的能量损失，提升光伏输出功率利用效率。在传统PI控制基础上，基于模糊PI控制理论，提出一种优化的PI控制模型，不仅可以扩大PI控制参数选择范围，还能够提升公共直流母线电压反应的快速性与稳定性。考虑超级电容充放电速率快且对其SOC采用限值管理，而现有研究很少考虑超级电容限值管理期间，所有高频分量全部由蓄电池承担对蓄电池带来的影响，因此本文考虑了在该限值期间，并提出一种新的功率限值能量管理方法，避免蓄电池承担过多高频功率分量，有效抑制蓄电池电流及电压剧烈波动，延长蓄电池使用寿命。通过仿真验证了所提方法的可行性与合理性。

1 改进反余切函数光伏MPPT控制

1.1 光储微电网系统模型架构

图1为光储微电网系统结构，包括：光伏系统、混合储能系统、交直流负荷、变换器、限值管理系统等[23]。图中：C1表示单向DC/DC变换器，实现升压和MPPT；C2表示双向DC/DC变换器，实现功率可控的充放电；C3为DC/AC逆变器，实现交流负荷接入直流母线；混合储能系统包括蓄电池与超级电容，通过限值管理系统（即超级电容SOC限值、蓄电池功率限值管理）对混合储能进行功率分配；光伏发电单元和储能单元通过各自DC/DC变换器汇总至公共直流母线；交流母线通过公共联接点PCC（point of common coupling）与大电网相连，该点处功率潮流双向流动。

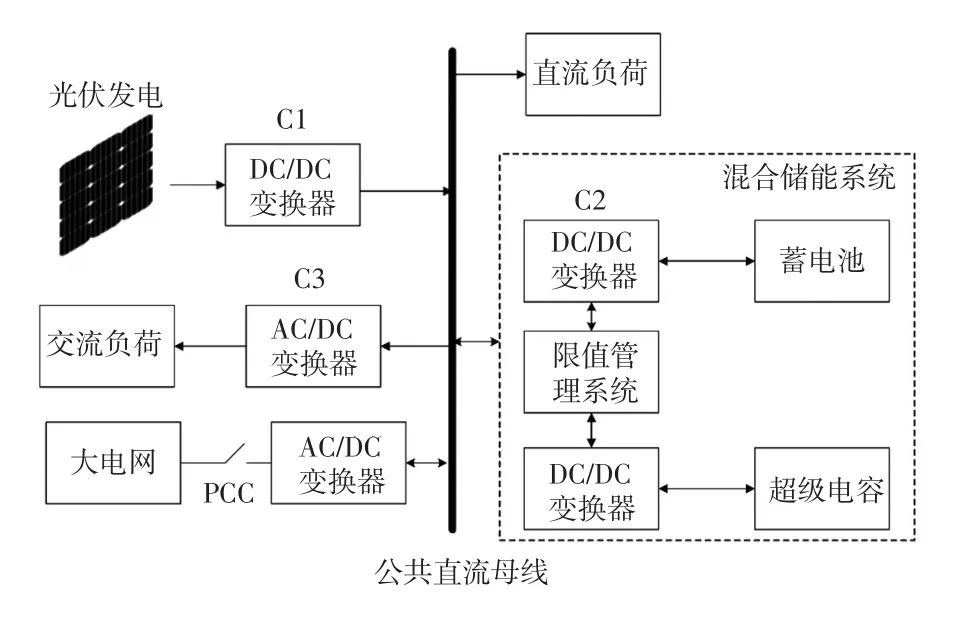
图1 光储微电网系统结构Fig.1 Structure of photovoltaic energy storage microgrid system

1.2 光伏最大功率点跟踪

光伏发电系统最大功率跟踪控制器采集光伏电池输出的电压和电流并对其分析，从而驱动DC/DC电路的功率开关管，实现光伏电池的MPPT控制。定步长电导增量法具有较好的效果，步长的大小决定了最大功率跟踪精度和速度。但考虑到其步长固定，因此不能同时满足跟踪速度和稳态精度要求。多数变步长电导增量法以固定大步长进行快速跟踪，再以固定小步长进行稳态跟踪；在步长间切换时会产生波动，且在稳态时也会有较小的波动。

1.2.1 光伏电池模型

当外界环境发生变化时，需要对传统光伏电池数学模型进行修正，使光伏模型能够适用于不同温度和光照条件[9]。修正公式为

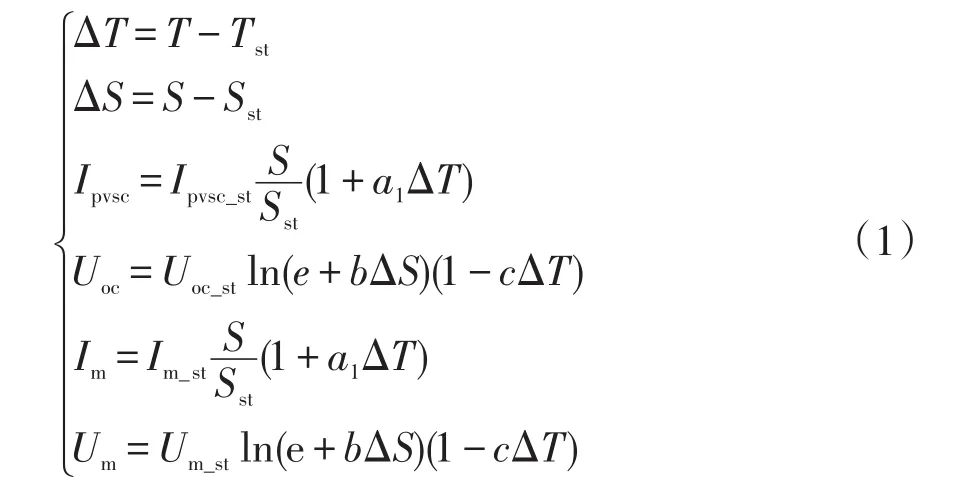
式中：Ipvsc和Ipvsc_st分别为当前光伏电池的短路电流和标准测试条件下电流，A；Uoc和Uoc_st分别为光伏电池开路电压和标准测试条件下电压，V；Im和Im_st分别为光伏电池的最大电流和标准测试条件下电流，A；Um和Um_st分别为光伏电池最大电压和标准测试条件下电压，V；e为自然对数的底数，其值约为2.718；a1、b、c补偿系数，参考取值：a1=0.002 5/℃，b=0.5/（W·m-2），c=0.002 88/℃；T为外界温度；Tst为标准测试条件下温度，取值为25℃；S为光照强度；Sst为标准测试条件下光照强度，取值为1 000 W/m2。该数学模型依据商家提供的4个技术参数就可以完成建模。

1.2.2 改进反余切函数变步长电导增量法

传统定步长电导增量法依据光伏电池输出功率-电压曲线斜率的性质，判断系统是否跟踪到最大功率点。光伏电池输出功率-电压曲线的一阶导数为

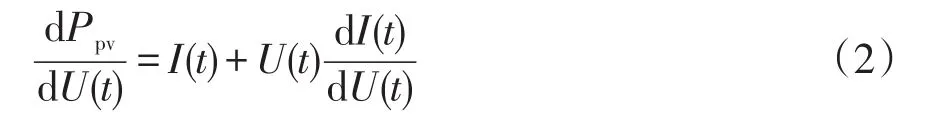
式中：Ppv为光伏功率；U（t）为光伏输出电压；（It）为光伏电流。若一阶导数大于0，表明运行工作点在最大功率点左侧；当一阶导数为0，则到达最大功率点；若一阶导数小于0，表明在最大功率点右侧。

针对变步长电导增量法中步长单一问题（前期固定大步长，后期固定小步长），提出一种新型变步长电导增量法，将0.8倍开路电压(0.8Uoc)及具有反余切函数变化趋势的变系数相结合的电导增量法。首先，将反余切函数与a的商，即作为|dP/dU|的变系数；其次，令反余切函数一阶导数，并计算得到；最后，实时调整小步长。反余切函数及变系数步长曲线趋势如图2所示。由图中曲线变化趋势可知，初始阶段步长相对较大（以k2为大步长），跟踪过程的后期步长相对较小（以k3为小步长），逐渐收敛于0。

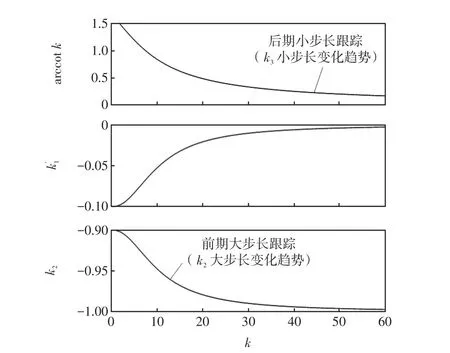
图2 反余切函数及变系数步长曲线趋势Fig.2 Trend of arc cotangent function and variable coefficient step curve

改进反余切函数变步长电导增量法MPPT算法实现步骤如下[10]。

步骤1MPPT算法依据光伏电池所处实际环境0.8Uoc快速跟踪到最大功率点的非线性区域附近。

步骤2以较大步长k2进行跟踪。当检测到电压U（t）大于0.8Uoc与电压变化量之和或者小于0.8Uoc与电压变化量之差时，继续以大步长k2进行快速跟踪，直至U(t)∈[Um-ΔU,Um+ΔU]，即MPPT跟踪到最大功率点附近的非线性区域内，MPPT算法即可进行最后的变步长稳定跟踪。

步骤3在最大功率点非线性区域内进行跟踪，检测电压变化量dU是否为0。当dU≠0，且电流变化量dI为0，说明系统已跟踪到最大功率点；当dI大于或小于0，表明工作点位于最大功率点左侧或者右侧，需要给电压增加或减少k3步长的扰动量。如果dU=0，且dI/dU=I（t）/U（t），表明系统在该时刻已经跟踪到最大功率点；如果dI/dU＞I（t）/U（t），则系统工作点位于最大功率点左侧，需要给电压增加k3的扰动量，向右扰动；否则减少k3的扰动量，使系统向左扰动。

2 考虑限值管理的混合储能能量管理控制策略

2.1 光储系统能量管理

混合储能系统的能量管理与协调控制直接影响系统的性能与经济性。图3为光储微电网能量管理系统控制策略流程。图中：SOC为超级电容荷电状态；SOC2为超级电容荷电状态；Ibatt、isc为流过蓄电池、超级电容电流；Ib-1-ref为经SOC2限值、功率限值管理后蓄电池电流参考值；Isc-1-ref为经SOC2限值、功率限值管理后超级电容电流参考值；Phess为系统剩余功率；Pbatt、Psc为蓄电池、超级电容参考功率；PL、PLD、PLS为负荷总功率及直流、交流负荷功率；Udc、Udc_ref为公共直流母线电压测量值、电压参考值；Psc为光伏功率；Pdc_ref为维持母线电压稳定所需功率参考值；Pgrid为功率差额约束条件。

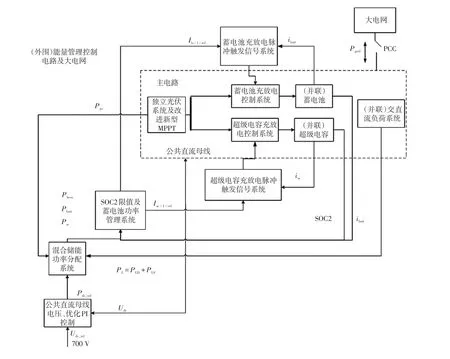
图3 光储微电网系统能量管理控制策略流程Fig.3 Flow chart of energy management control strategy for photovoltaic energy storage microgrid system

2.1.1 公共直流母线电压优化PI控制

直流母线电压与其他各系统的功率关系为

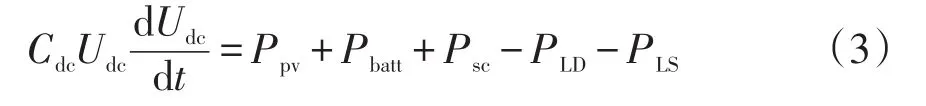
式中：CdcUdcdUdc/dt为维持母线电压稳定所需要的参考功率，即Pdc_ref；Cdc为直流侧储能电容。

母线电流为

传统PI控制将直流母线的参考电压Udc_ref和实测电压Udc的误差信号通过一个PI调节器得到参考电流idc_ref，从而获得维持直流母线稳定所需功率参考值Pdc_ref，控制过程如图4所示。

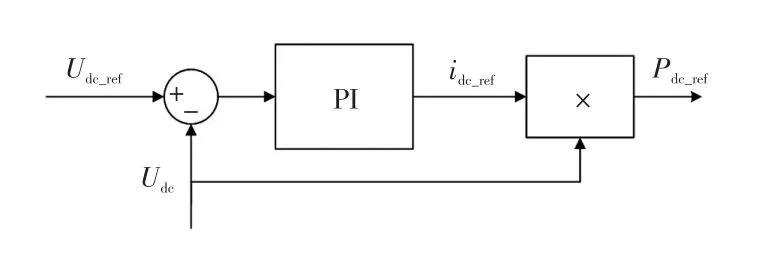
图4 传统PI控制模型Fig.4 Traditional PI control model

传统PI控制中，需要较准确的PI参数才能使直流母线电压快速地维持在平稳状态。基于模糊PI控制相关理论，对传统控制方法进行改进，优化传统PI控制。该优化方法在扩大PI控制参数选择范围的同时能够更好地实现母线电压稳定，同时克服模糊PI控制计算量大、运行时间长的缺点。控制过程如图5所示。

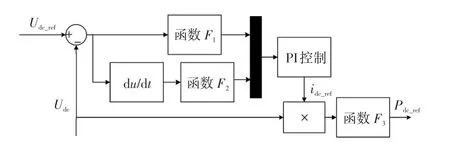
图5 优化PI控制模型Fig.5 Optimized PI control model

图5中：函数F1产生控制系数c1，该值与误差相关；函数F2产生控制系数c2，该值与误差变化率相关；函数F3产生比例系数p3，该值与Udc相关，具体可表示为

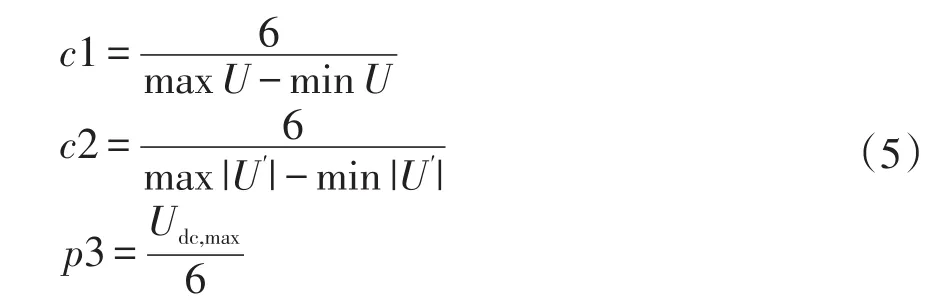
式中：maxU和minU分别为差值(Udc_ref-Udc)中的最大值与最小值；max|U′|和 min|U′|分别为差值(Udc_ref-Udc)的一阶导数绝对值的最大值与最小值；Udc,max为实测直流母线电压最大值。

2.1.2 混合储能功率分配

根据光储系统中剩余波动功率的大小对混合储能系统吸收或释放的功率进行分配，并参照运行期间SOC2及蓄电池承担高频分量，对储能元件的吸收或释放功率进行限制，可以优化系统的运行状态，延长混合储能设备的使用寿命。为维持系统功率平衡，混合储能系统需通过分配相应功率来满足负荷功率、光伏输出功率等的变动。混合储能系统承担的剩余波动功率表示为

2.2 功率限值管理混合储能控制策略

在HESS运行过程中，为了避免超级电容器的过充和过放，应根据其实时荷电状态设置限充、限放的界限[24]。本文在已有的混合储能系统超级电容荷电状态限值管理基础上，提出了对蓄电池承担高频功率分量限值控制方法。当超级电容限值后，为尽量减小高频功率分量对蓄电池电流、电压的影响，使蓄电池合理地消纳部分高频功率分量，将蓄电池消纳不了的多余高频功率分量通过PCC点闭合由大电网进行平抑，否则将PCC点断开。同时为减小大电网承担不平衡高频功率分量带来的不利影响，限制蓄电池允许承担高频功率分量的界限，分析如下。

（1）定义控制变量为

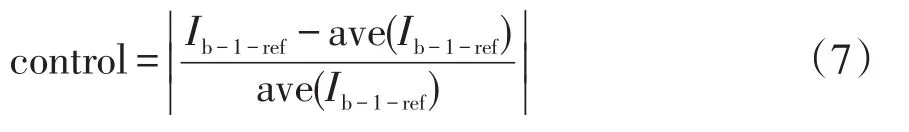
式中，Ib-1-ref为在SOC2限值与蓄电池限值承担高频功率分量期间（蓄电池功率限值期间）流过蓄电池的参考电流；ave(Ib-1-ref)为在超级电容SOC应限值但不进行限值运行条件下流过蓄电池的参考电流。计算得到的control作为一个控制变量，并将SOC2上、下限值（界限值）作为另一个控制变量。

（2）大电网处理的光储微电网系统功率差额约束条件变量，也即孤岛系统运行功率参数决定的约束为

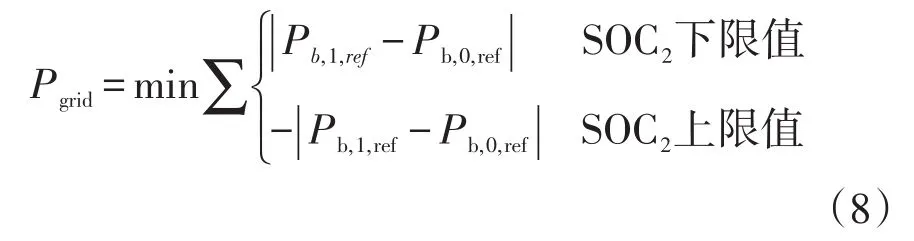
式中：Pb,1,ref为SOC2限值及蓄电池功率限值期间蓄电池承担的参考功率分量；Pb,0,ref为仅SOC2限值期间蓄电池承担的参考功率分量。尽量使得Pgrid与时间轴对称，在混合储能限值（SOC2及蓄电池功率限值）期间，使得通过PCC点的大电网承担不平衡高频功率分量总和最小。考虑到微电网容量较小，经功率限值管理后不平衡功率分量（Pgrid比例）更小，本文不考虑Pgrid对大电网的影响。

式（7）和式（8）共同确定蓄电池电流允许波动范围的限制区间[-b1b1]，以降低蓄电池电流波动的次数与幅度。图6给出了基于功率限值管理的混合储能控制流程。

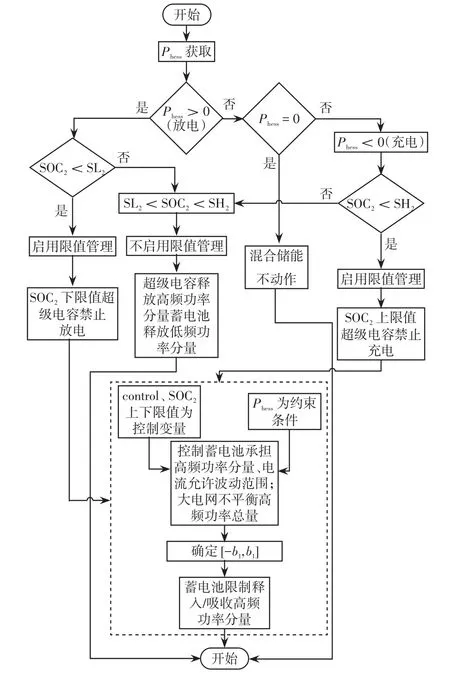
图6 基于功率限值管理混合储能控制流程Fig.6 Flow chart of hybrid energy storage control based on power limit management

图中，SL2与SH2分别表示SOC2下限值与上限值，分别设置为20%和80%。

3 算例分析

为验证所提出的控制策略及光储能量管理系统的适用性与有效性，搭建经典光储微电网系统模型进行分析[16]。设置模型仿真时间为2 s，光伏发电功率在0.8 s时发生突变，负荷随机变动，以验证控制策略的可行性。考虑蓄电池SOC变化缓慢，假定在运行期间蓄电池荷电状态运行在合理区间范围内。主电路与控制电路模块主要运行参数如表1所示。

表1 主要参数Tab.1 Main parameters

仿真期间设置改进新型MPPT中变量k范围为[0，60]，并获取系统中指标数据进行控制分析。图7给出了变步长电导增量法与改进反余切函数变步长电导增量法光伏输出功率对比。0.8 s前输出参考功率约为3 745 W，0.8 s后输出参考功率约为3 400 W；0.3～0.8 s期间传统变步长电导增量法输出功率的波动范围约为[3 680 W，3 765 W]，相对于参考功率，输出功率最大波动率（功率最大值与最小值之差除以输出参考功率）为2.27%，且在该运行时间内功率波动幅度较大，稳态波动明显；改进方法中输出功率的波动范围约为[3 742 W，3 765 W]，输出功率最大波动率为0.06%，输出功率波动幅度明显减小；在0.80～1.36 s间波动幅度与功率波动率也相对较小。分析结果表明，改进型方法具有更好的稳态精度，能够减小稳态波动的幅度，降低光伏输出功率波动损失。

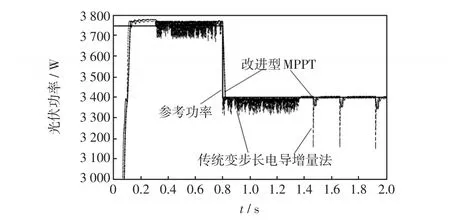
图7 光伏输出功率对比Fig.7 Comparison of photovoltaic output power

在其他模型参数一致情形下，分别采用传统PI控制与优化PI控制进行对比分析，优化方法中参数如表1所示。图8给出了传统PI控制与优化PI控制情况下直流母线电压对比。当PI参数为0.2、0时，图8（a）表明：传统PI控制使得直流母线电压趋于平稳但速度较慢，1.0 s后趋于稳定；优化PI控制使得直流母线电压能够快速趋于稳定（约0.45 s）。图8（b）表明，当PI参数为0.25、0.50时，传统PI控制下直流母线电压波形变化较大，出现较为严重的超调现象，且电压平稳缓慢，1.8 s后逐渐趋于稳定，而优化PI控制使得电压更快更平滑的趋于平稳。从图8可以看出，传统方法控制效果对PI参数要求较高，需要合适的参数才能使得直流母线电压较好地趋于稳定，优化PI控制方法能够在PI参数波动较大范围内，仍使得直流母线电压具有快速的稳定性，扩大了PI参数平稳电压范围。

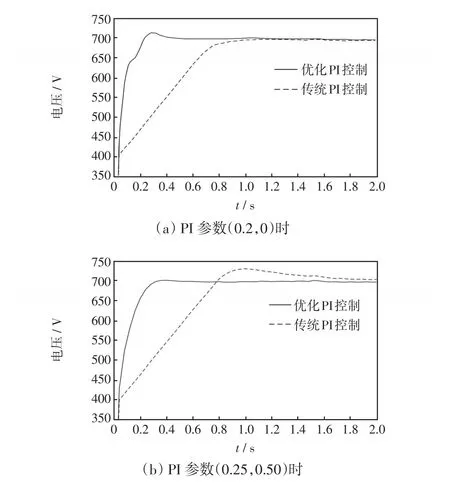
图8 PI控制公共直流母线电压对比Fig.8 Comparison of common DC bus voltage between PI controls

当HESS承担的功率波动较大时，超级电容SOC限值期间，依据式（7）和式（8）条件，设置流过蓄电池电流的波动范围限制(b1)。大电网相比于微网具有很强的承受波动的能力，故当SOC2已达到限值，且蓄电池充放电的电流允许波动超出范围后，将多余高频功率分量交由大电网进行消纳；在SOC2及蓄电池功率限值期间（或一个周期内），尽量使向电网投入与吸收的高频分量总量最小。本文通过大量仿真分析，获取经验数据，确定蓄电池电流允许波动范围界限设置为[-0.012 5，0.012 5]，即允许蓄电池电流相对于正常运行（SOC2应限值但不限值运行）情况下电流波动的2.5%左右。

电网消纳的功率差额曲线如图9所示，可见，达到了较理想的控制效果，其中图9（b）和（c）分别表示超级电容SOC下限值与上限值期间功率差额曲线放大。算例分析中以超级电容SOC限值上限（SOC2达到上限但仍有富余功率）、蓄电池有无采用功率限值为例进行分析，混合储能系统中以充电电流为负，放电电流为正。

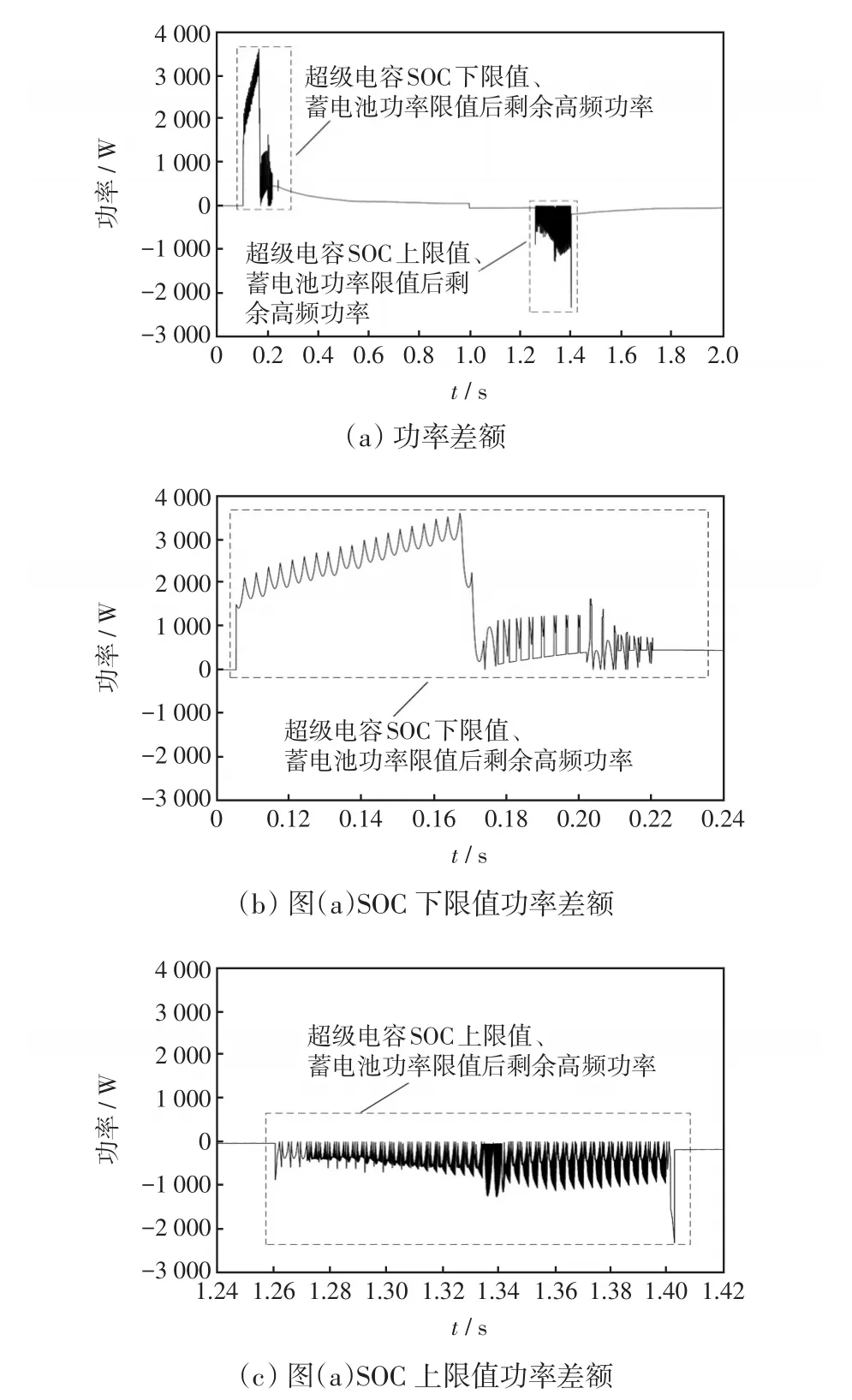
图9 电网消纳功率差额曲线Fig.9 Power consumption difference curves of power grid

图10给出了蓄电池采用功率限值管理前后时蓄电池电流局部放大。图10（a）表示SOC2限值但蓄电池未功率限值期间（1.25～1.40 s），蓄电池承担系统所有高频功率分量时电流曲线（相当于b1值设置较大（0.05）），其电流波动范围相比于正常运行情况下电流变化幅度的10%左右；在该情况下电流波动次数急剧增加，降低了蓄电池使用寿命[21-22]；当此剧烈波动现象发生在蓄电池充放电界限处时，表明蓄电池短期内充放电次数增加，也将严重影响其使用寿命[20]，应避免该现象产生。图10（b）给出了功率限值期间蓄电池电流曲线，与图10（a）相比电流波动次数与幅度明显改善，能够避免蓄电池电流急剧变化对其寿命的影响。依据蓄电池电压与电流关系可以得出蓄电池电压波动次数与幅度也相对减小，不再赘述。

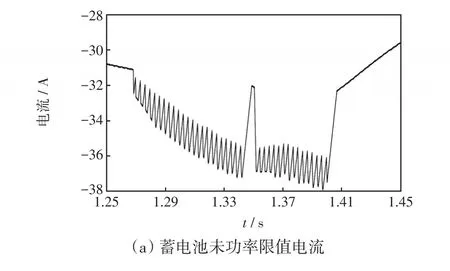
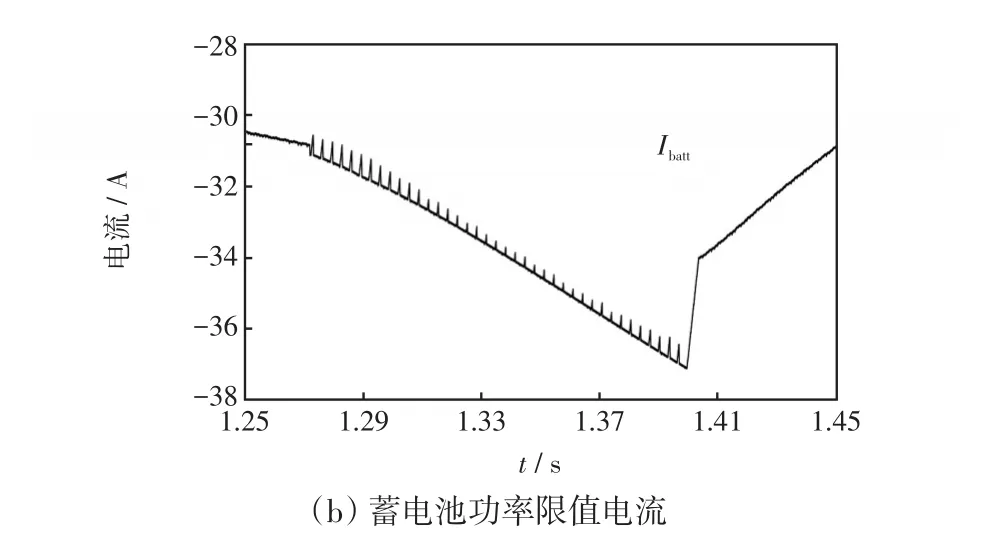
图10 蓄电池有无功率限值期间电流波动曲线Fig.10 Current fluctuation curves of battery with or without power limit management

4 结论

本文搭建了光储微电网系统模型，针对光伏MPPT提出一种改进新型变步长电导增量法，提升光伏输出功率利用效率；在传统PI控制基础上进行优化PI控制，使得直流母线电压能够快速地趋于稳定；对蓄电池在SOC2限值期间承担的高频功率分量进行限制，避免流过其电流、电压急剧变化。通过模型进行了验证分析，得出如下结论。

（1）结合0.8Uoc、反余切函数及光伏功率-电压曲线自身特性，提出了改进新型变步长电导增量法进行光伏MPPT，该方法能够较好地跟踪光伏最大功率，有效减少功率波动引起的能量损失。

（2）依据模糊PI控制理论，在传统PI控制基础上进行改进，提出了优化PI控制方法，该优化方法能够有效扩大PI参数设置的适应度范围，降低了控制系统中对PI参数的要求范围，同时能够使得直流母线电压更快地趋于稳定，减小电压稳定过程缓慢及超调现象对系统稳定的不利影响。

（3）针对超级电容SOC限值管理期间，系统高频功率分量处理问题，提出了对蓄电池充放电功率限值管理策略，避免蓄电池在SOC2限值期间承担过多的高频功率分量使流过蓄电池电流、电压频繁波动对其造成的损害，延长蓄电池使用期限，提升混合储能系统经济效益。