非理想通信环境下主动配电网多源协同调控策略
2022-12-15田美君刘沈全汪隆君曾德辉
田美君,刘沈全,汪隆君,王 钢,曾德辉
(1.华南理工大学电力学院,广州 510640;2.广州嘉缘电力科技有限公司,广州 510610)
分布式电源规模化接入配电网是电力系统发展的趋势之一,给配电网的安全、经济运行带来了巨大挑战。主动配电网ADN(active distribution network)技术应用先进的网络通信技术与调控策略对分布式电源进行主动管理与调控,是实现分布式电源有序并网、可再生能源高效消纳的重要技术路径。
如何确保多种分布式电源的协同运行,是主动配电网亟待解决的问题。传统配电网采用集中式调控策略[1-2],当分布式电源大规模并网后,该策略使调控中心运算负担显著增加,无法较好地应对分布式电源“即插即用”的运行特性,使得主动配电网无法容纳大量分布式电源,且该策略对于通信时延等非理想通信因素的容错性也较低,难以满足主动配电网的技术需求[3-4]。
为避免集中式调控策略的局限性,有学者提出分布式协同调控策略[5-6]。该策略通过节点间相互通信、各控制器并行处理数据的方式,实现分布式自主控制,虽可以减轻调控中心的运算负担[7],但这种调控策略[8-12]需要遍历网络中通信节点的信息,增加运算复杂度的同时放大了通信时延等非理想通信因素对运算速度与准确性的影响,且要求所有节点均安装可靠的通信与控制装置,经济性较差。
对此,有学者综合集中式与分布式调控策略的优点,提出了半集中式-半分布式的调控策略[13],其典型代表为基于Leader-Follower一致性算法的调控策略。该策略仅需要在部分节点安装控制装置,且可通过调整通信网络中领导节点接收到的联络线功率补偿控制信号,实现对配电网联络线功率指令值的快速可靠跟踪。然而,目前针对这种调控策略的研究大多默认领导节点能够直接测量或计算配电网的功率缺额,没有指出其中的具体办法[14-16]。大多数研究采用配电网联络线功率偏差的比例项作为功率补偿控制信号,容易造成联络线功率产生较大偏差[15,17]。
此外,现有研究提出的调控策略常基于理想通讯环境[18-20],对非理想通信环境的考虑较为欠缺,对非理想通信因素的分析不够全面。文献[21]仅分析了通信时延、信道噪声等对协同控制的影响,并未对实际运行过程中存在的节点通信故障情况予以考虑;文献[14,22]仅考虑了普通节点通信故障的情况,并未考虑领导节点通信故障的情况;文献[15]仅分析了非理想通信环境对算法收敛性的影响,并未给出抑制这种影响的具体办法。另外,部分研究仅从配电网经济运行的角度对分布式电源进行有功输出的协同控制,缺少对于无功输出的协同控制以及对配电网电压均衡的考虑[23-24]。
为实现非理想通信环境下主动配电网的分布式电源协同运行,本文提出综合经济性和电压均衡技术指标的多源协同调控策略。首先,考虑非理想通信环境中通信时延、信道噪声等因素的影响,提出基于熵权法的一致性算法状态转移矩阵改进方法;其次,提出在配电网联络线功率补偿控制信号中引入积分控制项,以实现对联络线功率指令值的快速、无差跟踪;接着,在分布式协同调控策略中结合集中式通信,提出变结构通信的实现方法;进而,以改进一致性算法为基础,建立非理想通信环境下考虑多种分布式电源功率特性的主动配电网多源协同调控模型。最后,通过仿真验证所提策略的有效性。
1 基于一致性理论的分布式控制
1.1 图论概述
主动配电网中各节点通过通信网络进行信息交互。本文以无向图G=(V,E)表示多源协同控制的通信网络拓扑,其中,V为节点的集合,E为边的集合。若节点i与节点j间存在通信信道,则记为(i,j)∈E。无向图G的拓扑结构可用对称n阶方阵表示,其元素aij定义为
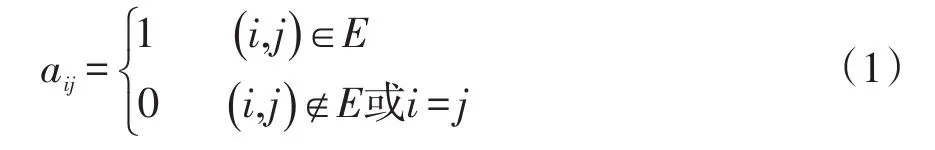
节点连通度为与节点直接相连的节点个数,记无向图G中节点i的连通度为di,节点连通度矩阵为D=diag(d1,d2,…,dn);在此基础上,得出无向图G的拉普拉斯矩阵为L=D-A,记为

式中,lij为拉普拉斯矩阵中第i行第j列的元素。
1.2 理想通信环境下的一阶离散一致性算法
一致性算法通过规定各节点的控制协议,利用节点间少量信息交互、自主控制,最终使分布式控制系统中各节点的状态变量,如电压、电流、频率、增量成本等,收敛于稳定的共同值。其中,各节点的状态变量也称为一致性变量,记xi(t)为节点i在t时刻的一致性变量。
为维持配电网联络线功率于指令值,本文使用结合牵引策略的Leader-Follower离散型一致性算法,其表示为
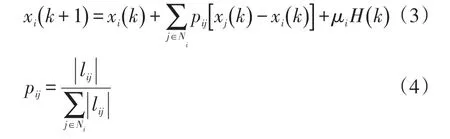
式中:k为离散时间序列;Ni为与节点i相连的节点集合;pij为状态转移矩阵的元素;H(k)为领导节点的牵引控制项,选定为配电网联络线功率补偿控制信号;μi为领导节点牵引控制项系数,当节点i为领导节点时,μi取1,否则取0。
2 非理想通信环境下的改进一致性算法
2.1 考虑非理想通信因素的改进一致性算法
非理想通信因素会使多源协同调控传输的数据偏离准确值,从而影响分布式算法的收敛速度以及求解准确性。设xij(k)为非理想通信环境下k时刻节点i接收到节点j发送的一致性变量,其表示为
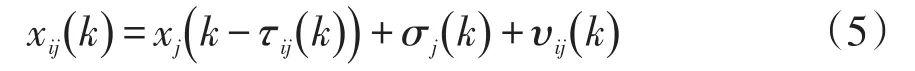
式中:τij(k)为通信时延;σj(k)为测量误差;υij(k)为信道噪声。
为减少通信时延的影响,加快算法收敛,本文在一致性算法中引入增益调整函数c(k),有

在满足式(6)条件下,c(k)可保证在信道噪声、测量误差影响下,一致性算法仍能收敛且静态误差有界[25]。于是,一致性算法可表示为
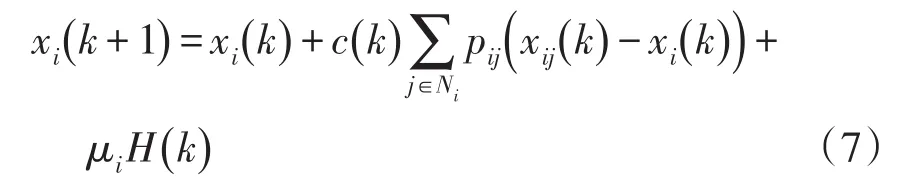
为加快算法收敛速度,依据文献[16]所得实验结果,本文取。
2.2 基于熵权法的改进状态转移矩阵
在引入增益调整函数的基础上,为进一步降低通信时延对算法收敛速度的影响,本文利用熵权法依据通信时延以及节点的连通度给出相邻节点对应的权重,以此改进状态转移矩阵P。改进后状态转移矩阵的元素表示为
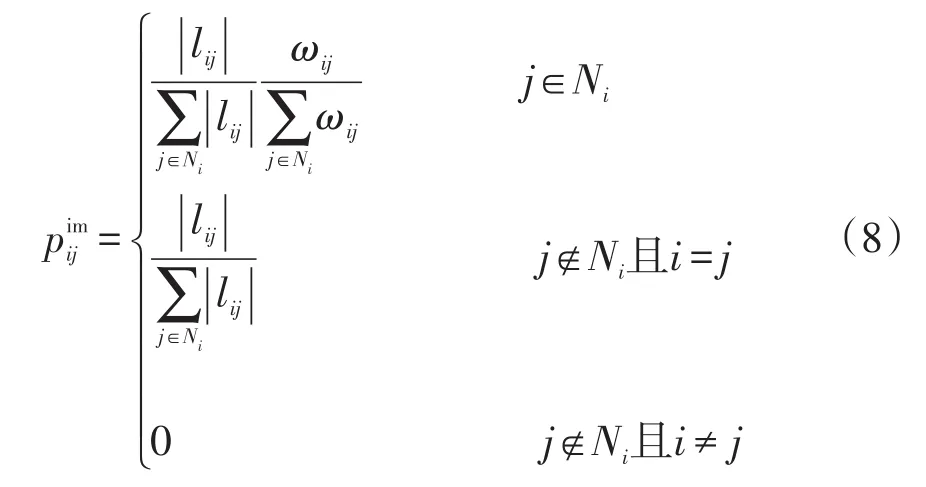
式中,ωij为相邻节点j对节点i的重要程度,ωij=ωi,tτij+ωi,ddj,ωi,t为节点i通信时延的指标权重,ωi,d为节点i节点连通度的指标权重。
2.3 基于比例-积分控制的领导节点牵引控制项
为了减少跟踪配电网联络线功率时的稳态误差,本文基于比例-积分控制原理构造领导节点的牵引控制项,有功和无功补偿控制信号HP和HQ分别为
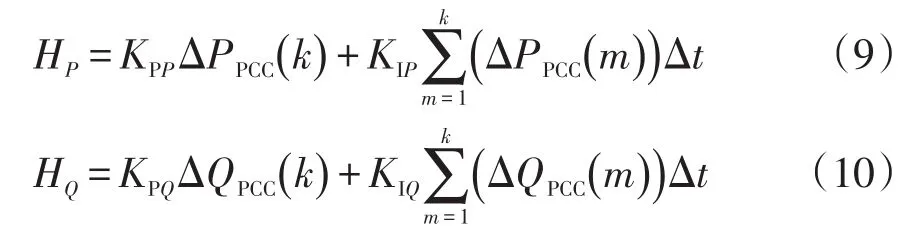
式中:KPP、KPQ为比例控制参数;KIP、KIQ为积分控制参数;Δt为调度时间步长;ΔPPCC(k) 、ΔQPCC(k)分别为配电网联络线实时有功和无功功率PPCC(k) 、QPCC(k)与相应有功和无功指令值PPCC,ref(k)、QPCC,ref(k)间的偏差。
综上,非理想通信环境下的改进一致性算法可表示为
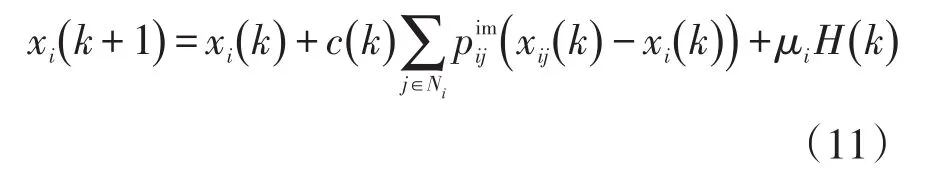
2.4 结合集中式通信的变通信结构调控策略
除通信时延、信道噪声等非理想通信因素外,通信线路故障、网络攻击等情况也会导致节点间无法正常进行信息交互,影响算法性能,甚至破坏配电网安全稳定运行。
对此,本文提出了结合集中式通信的变通信结构多源协同分布式调控策略,如图1所示。
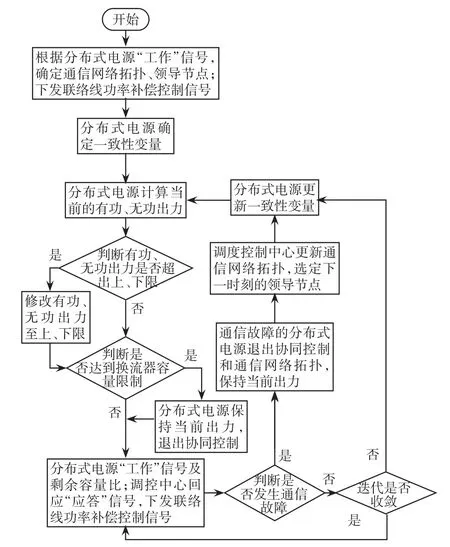
图1 主动配电网多源协同调控策略流程Fig.1 Flow chart of multi-source coordinated control strategy for ADN
该策略的具体流程步骤如下。
步骤1初始化。对于调控中心,根据分布式电源发送的“工作”信号确定初始通信网络拓扑及领导节点,并向作为领导节点的分布式电源下发配电网联络线功率补偿控制信号;对于分布式电源,确定初始一致性变量。
步骤2分布式电源依据信息交互后得到的一致性变量计算当前的有功、无功出力,并判断有功、无功出力是否超出上、下限,若超出上、下限,则将出力调整至上、下限。
步骤3分布式电源依据计算得到的有功、无功出力,判断输出功率是否超出换流器容量限制,若超出限制,则分布式电源维持当前出力,退出协同控制。
步骤4分布式电源向调控中心发送“工作”信号及剩余容量比;调控中心回应“应答”信号,同时向领导节点下发联络线功率补偿控制信号。
步骤5调控中心和分布式电源分别根据分布式电源发送的“工作”信号和调控中心回应的“应答”信号,各自判断是否发生通信故障,若发生通信故障,则转至步骤6,否则转至步骤7。
步骤6对于调控中心,根据接收的分布式电源“工作”信号,及时更新通信网络拓扑,并选定下一时刻的领导节点,领导节点选取原则为:优先选取节点连通度大且剩余容量比大的非可再生分布式电源作为领导节点;同时,对于通信故障的分布式电源,则退出协同控制和通信拓扑,并维持当前出力不变,转至步骤8。
步骤7各节点判断一致性算法是否收敛,若仍未收敛,则转至步骤8,否则转至步骤4。
步骤8分布式电源更新一致性变量,转至步骤2。
该策略在循环运行时可实现分布式电源个体间的信息交互与自主控制,进而有效减轻调控中心的通信与计算负担,使配电网能够拓展容纳更多的分布式电源。同时该策略也能解决分布式电源节点通信故障等造成的通信网络拓扑多变问题,并且确保对联络线功率的可靠追踪及对分布式电源剩余容量的合理利用,最终实现主动配电网的经济、安全、可靠运行。
3 基于一致性算法的多源协同调控
3.1 多类型电源运行成本建模
1)风力发电机WT(wind turbine)模型
选取双馈异步风力发电机为原型,为高效利用风能,设弃风成本为目标函数,风力发电机在最大功率点跟踪MPPT(maximum power point tracking)模式下的最大输出有功限制、最大定子电流限制、最大转子电流限制、变流器容量限制为约束条件。考虑市场机制下弃风造成的费用损失,本文将弃风成本构造成二次函数[8,21],具体模型为
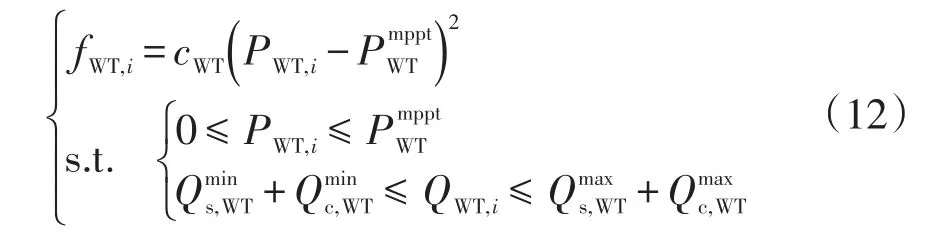
式中:cWT为弃风单位成本;PWT,i、QWT,i分别为风力发电机输出有功功率、无功功率;为MPPT模式下的最大输出有功功率;为定子侧输出无功功率上、下限;为网侧变流器输出无功功率上、下限。
2)光伏PV(photovoltaic)发电模型
为尽可能消纳光伏发电,设弃光成本为目标函数,光伏发电在MPPT模式下最大输出有功限制、逆变器容量限制为约束条件。考虑市场机制下弃光造成的费用损失,本文将弃光成本构造成二次函数[8,21],具体模型为
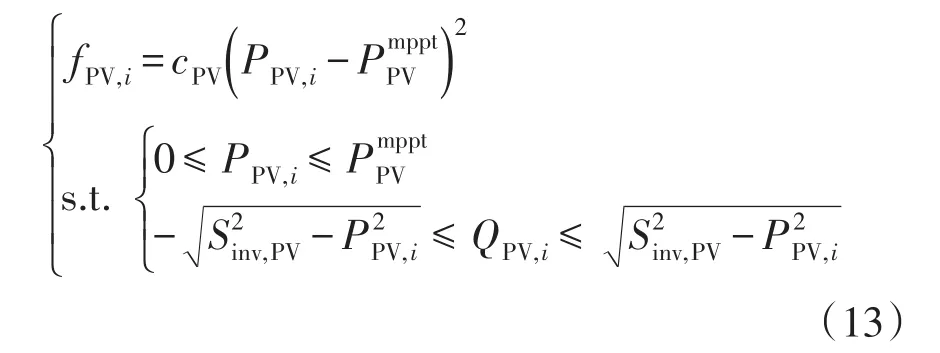
式中:cPV为弃光单位成本;PPV,i、QPV,i分别为光伏发电输出有功功率、无功功率;为在MPPT模式下最大输出有功功率;Sinv,PV为逆变器容量。
3)微型燃气轮机MT(micro gas turbine)模型
设运行成本为目标函数,微型燃气轮机有功输出上下限、变流器容量限制为约束条件。微型燃气轮机的运行成本可由二次函数拟合得出[18],具体模型为
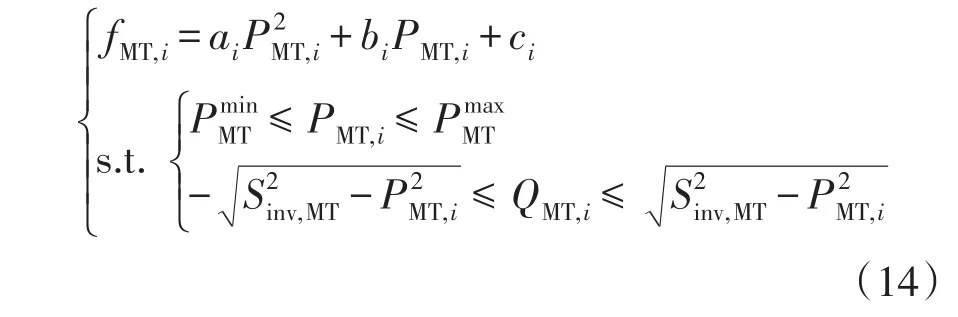
式中:PMT,i、QMT,i分别为微型燃气轮机输出有功功率、无功功率;ai、bi、ci为运行成本系数;P为输出有功功率上、下限;Sinv,MT为变流器容量。
4)储能装置ESS(energy storage system)模型
设充放电成本为目标函数,储能装置充放电上下限、逆变器容量限制为约束条件。储能装置的充放电成本可由过原点且开口向上的二次函数拟合得出[21],具体模型为
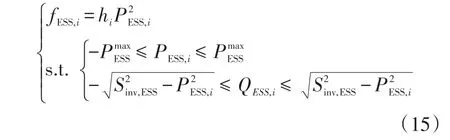
式中:PESS,i、QESS,i分别为储能输出有功功率、无功功率;hi为充放电成本系数;为充放电功率上限;Sinv,ESS为逆变器容量。
3.2 多源协同调控一致性算法模型
1)有功控制模型
为实现主动配电网经济运行,以分布式电源总运行成本为分布式电源控制有功输出的目标函数为

式中:ΩDG为分布式电源节点集合;fDG,i为节点i处分布式电源的运行成本。约束条件包括式(11)~式(14),以及配电网有功功率平衡约束,即
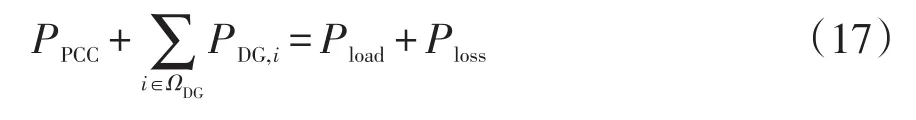
式中:Pload为配电网总有功负荷;Ploss为有功网损。由于有功控制模型中含有等式约束和不等式约束,根据拉格朗日乘子法以及卡罗需-库恩-塔克KKT(Karush-Kuhn-Tucker)条件,对由有功控制模型构造的拉格朗日函数进行求导可得:当各分布式电源运行成本微增率一致时,分布式电源总运行成本达到最小。因此,取各分布式电源的运行成本微增率为其一致性变量xP,i,即
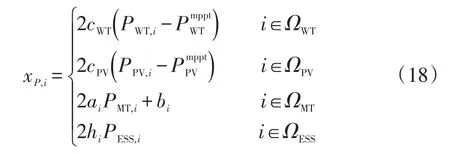
式中:ΩWT为风力发电机节点集合;ΩPV为光伏发电节点集合;ΩMT为微型燃气轮机节点集合;ΩESS为储能装置节点集合。则在非理想通信环境下各分布式电源关于有功出力的一致性变量可表示为
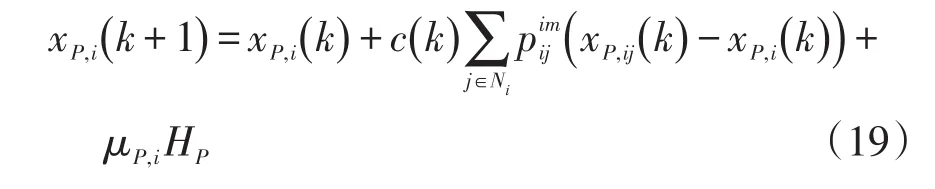
式中,μP,i为领导节点有功牵引控制项系数。
2)无功控制模型
为了保证主动配电网安全运行,以分布式电源节点电压均衡为目标控制分布式电源的无功输出,约束条件包括:式(11)~式(14),以及配电网无功功率平衡约束,即
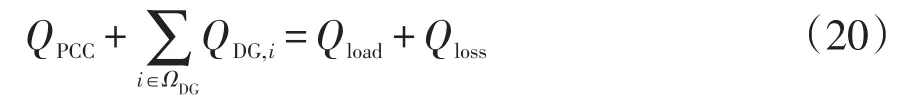
式中:Qload为配电网总无功负荷;Qloss为无功网损。
取分布式电源节点电压与基准电压的偏差为其一致性变量xQ,i对分布式电源的无功进行控制,即
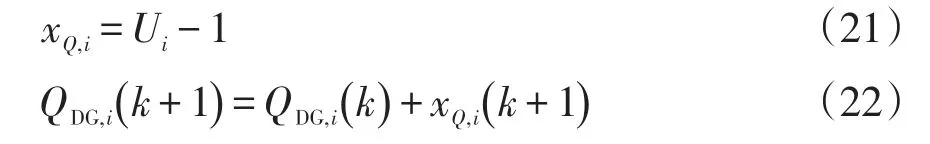
式中,Ui为节点i的实际电压标幺值。则在非理想通信环境下各分布式电源关于无功出力的一致性变量可表示为

式中,μQ,i为领导节点无功牵引控制项系数。
4 算例验证
选取如图2所示的含风力发电、光伏发电、微型燃气轮机以及储能装置的10 kV主动配电网为算例,进行仿真验证。配电网总负荷为(2.124+j0.896)MV·A,功率基准值为1 MV·A。
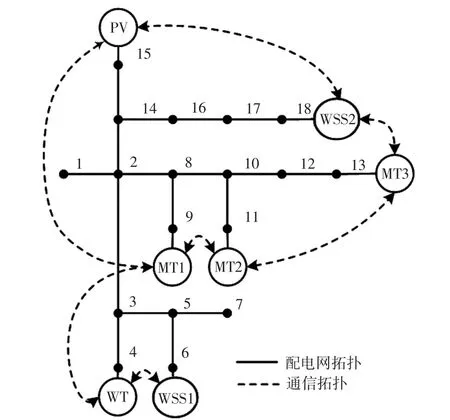
图2 主动配电网拓扑Fig.2 Topology of ADN
设调度时间步长为0.01 s;各通信节点间的通信时延服从上限为0.1 s、下限为0 s的截断正态分布,其均值为0,方差为0.025;信道噪声以及测量误差服从均值为0、方差为0.025的正态分布;MT1为初始领导节点;配电网联络线的初始有功指令值为-0.1 MW,无功指令值为0.2 Mvar。表1和表2分别列出了分布式电源的基本参数和主动配电网的网络拓扑参数。
该算例验证基于Matlab R2019a平台,所有测试运算均在CPU主频为3.40 GHz、内存为8 GB的Windows10 64位计算机上进行。
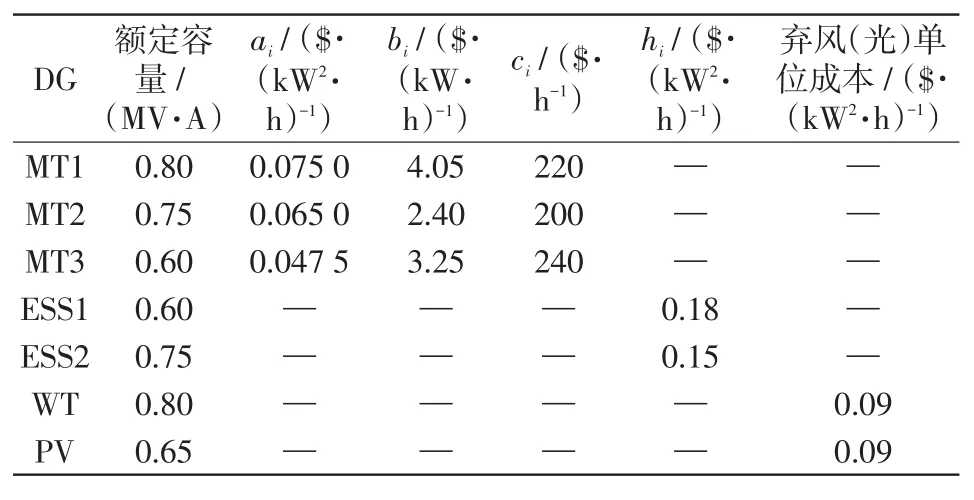
表1 分布式电源的基本参数Tab.1 Basic parameters of distributed generators
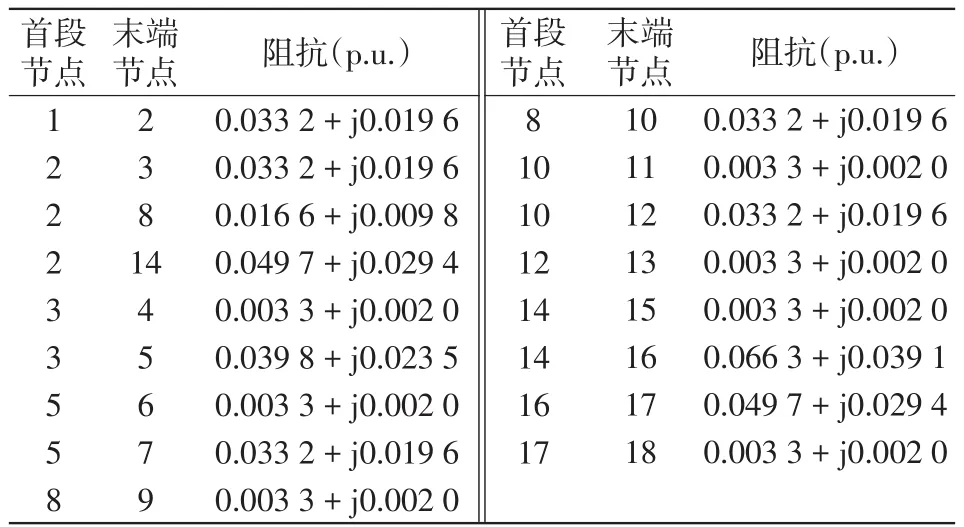
表2 主动配电网的网络拓扑参数Tab.2 Network topological parameters of ADN
4.1 改进状态转移矩阵的影响
为验证改进状态转移矩阵对一致性算法收敛性的影响,本文分别采用改进前以及改进后的状态转移矩阵进行了仿真,仿真结果如图3所示。

图3 改进状态转移矩阵前后一致性变量迭代过程Fig.3 Convergence process of consensus variable with and without the improvement of state transition matrix
由图3(a)可见,在未改进节点转移矩阵前,各分布式电源的成本微增率收敛速度较慢;在10 s时,成本微增率仍有较大收敛误差。由图3(b)可见,改进节点转移矩阵后,各分布式电源的成本微增率在6 s时已基本收敛。由仿真结果对比可知,改进后的状态转移矩阵能够减少通信时延对一致性算法收敛性的影响,能够加快一致性算法在应对非理想通信环境下的收敛速度。
4.2 引入比例-积分控制项的影响
为观察在联络线功率补偿控制信号中引入积分控制项的影响,本文通过迭代仿真得出了不同比例积分控制参数下多源协同控制系统收敛时配电网联络线的功率偏差值,如表3所示。

表3 不同比例积分控制参数下主动配电网联络线功率偏差Tab.3 Deviations of ADN tie line power with different PI control parameters
由表3可知,在联络线功率补偿控制信号中仅含有比例项时,配电网联络线无功功率偏差比较大,为kvar级别;在引入积分项后,不仅配电网联络线有功功率偏差减小,而且无功功率偏差减小尤其明显。
4.3 通信故障场景
为测试所提策略在通信故障时的整体控制效果,本文进行普通节点通信故障、领导节点通信故障2种不同场景下的仿真验证。
1)普通节点通信故障
设6 s时普通节点MT3突然出现通信故障,“工作”信号发送失败,因此被迫退出通信网络拓扑和多源协同控制,但继续维持原有出力。由于在规定时间内没有接收到MT3的“工作”信号,调控中心更新通信网络拓扑。由于多源协同调控并未达到调控目标,各分布式电源功率以及电压继续经历调控,通信正常的分布式电源继续通过一致性变量的信息交互自主控制,直至各通信正常的分布式电源一致性变量完全收敛且配电网联络线功率恢复至指令值。普通节点通信故障仿真结果如图4所示,可见,约8 s时各通信正常的分布式电源一致性变量收敛于共同的稳定值,配电网联络线的有功功率、无功功率也稳定至指令值;12 s时调控中心更新该时段配电网联络线功率的指令值,令有功指令值为0、无功指令值为0.15 Mvar。通信故障的机组继续维持原有出力,通信正常的分布式电源则共同响应调控中心,通过各自的控制器调节有功、无功出力,使各机组的一致性变量收敛,同时使配电网联络线实际功率快速可靠地调整至功率指令值。
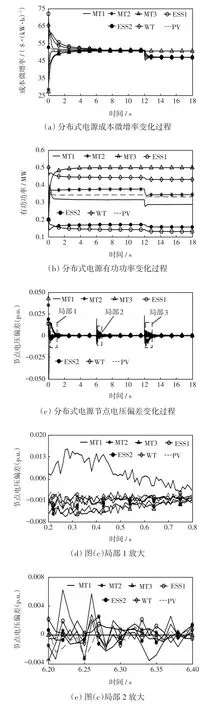
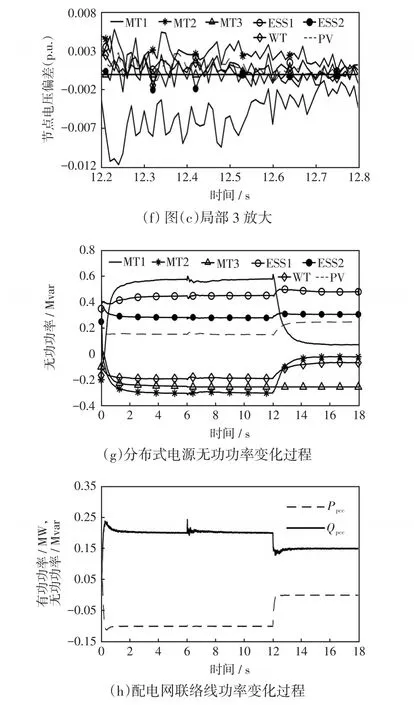
图4 普通节点通信故障情况下多源协同调控策略仿真结果Fig.4 Simulation results of multi-source coordinated control strategy in the case of communication failure at ordinary node
2)领导节点通信故障
设6 s时领导节点MT1突然出现通信故障,“工作”信号发送失败,被迫退出通信网络拓扑,无法参与协同控制。领导节点通信故障导致原全连通的通信网络拓扑被分为由 MT2、MT3、ESS2、PV 和WT、ESS1组成的2个独立连通拓扑。由于在规定时间内没有接收到MT1的“工作”信号,调控中心更新通信网络拓扑,并依据节点连通度、剩余容量比及分布式电源性质,选取ESS1、ESS2为2个独立连通拓扑的领导节点,并发送配电网联络线功率补偿控制信号至2个新的领导节点。领导节点通信故障时仿真结果如图5所示,可见,由于仍未达到调控目标,两组分布式电源继续自主进行协同控制,共同承担调整配电网联络线功率的任务,再经过约2 s,两组分布式电源的节点电压偏差达到一致性收敛,配电网联络线功率也稳定到指令值。在12 s时,调控中心更新该时段配电网联络线功率的指令值,令有功指令值为-0.05 MW、无功指令值为0.1 Mvar。如图5所示,2组分布式电源快速响应调控中心下达的功率控制信号,约14 s时,两组分布式电源的一致性变量收敛,配电网联络线功率达到指令值。
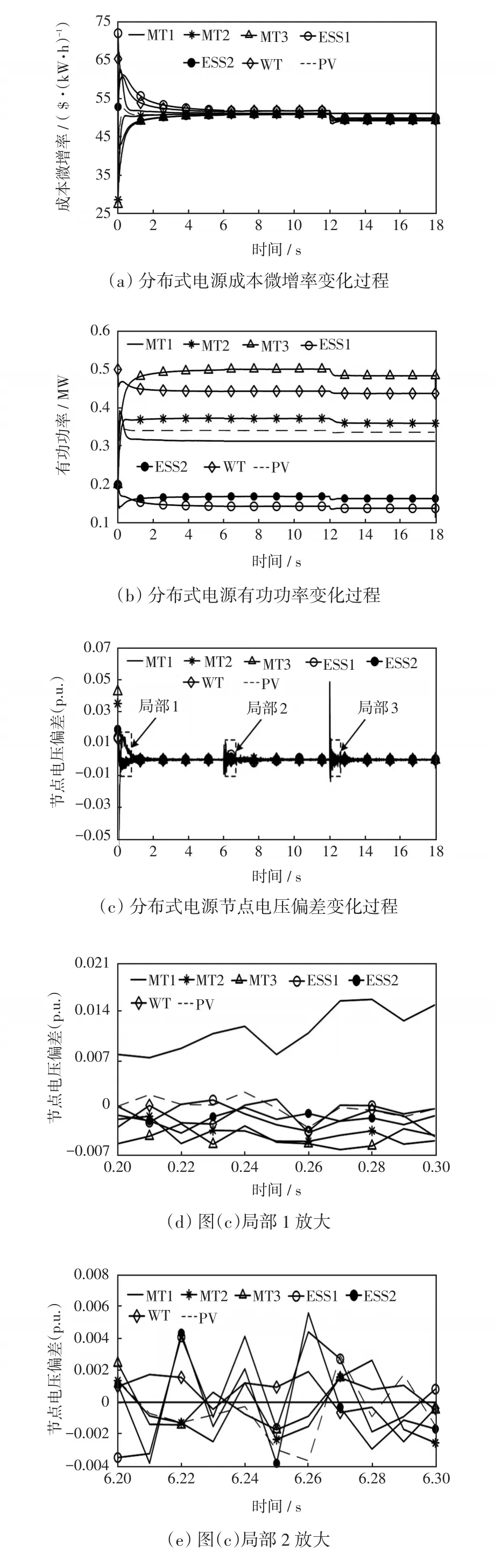
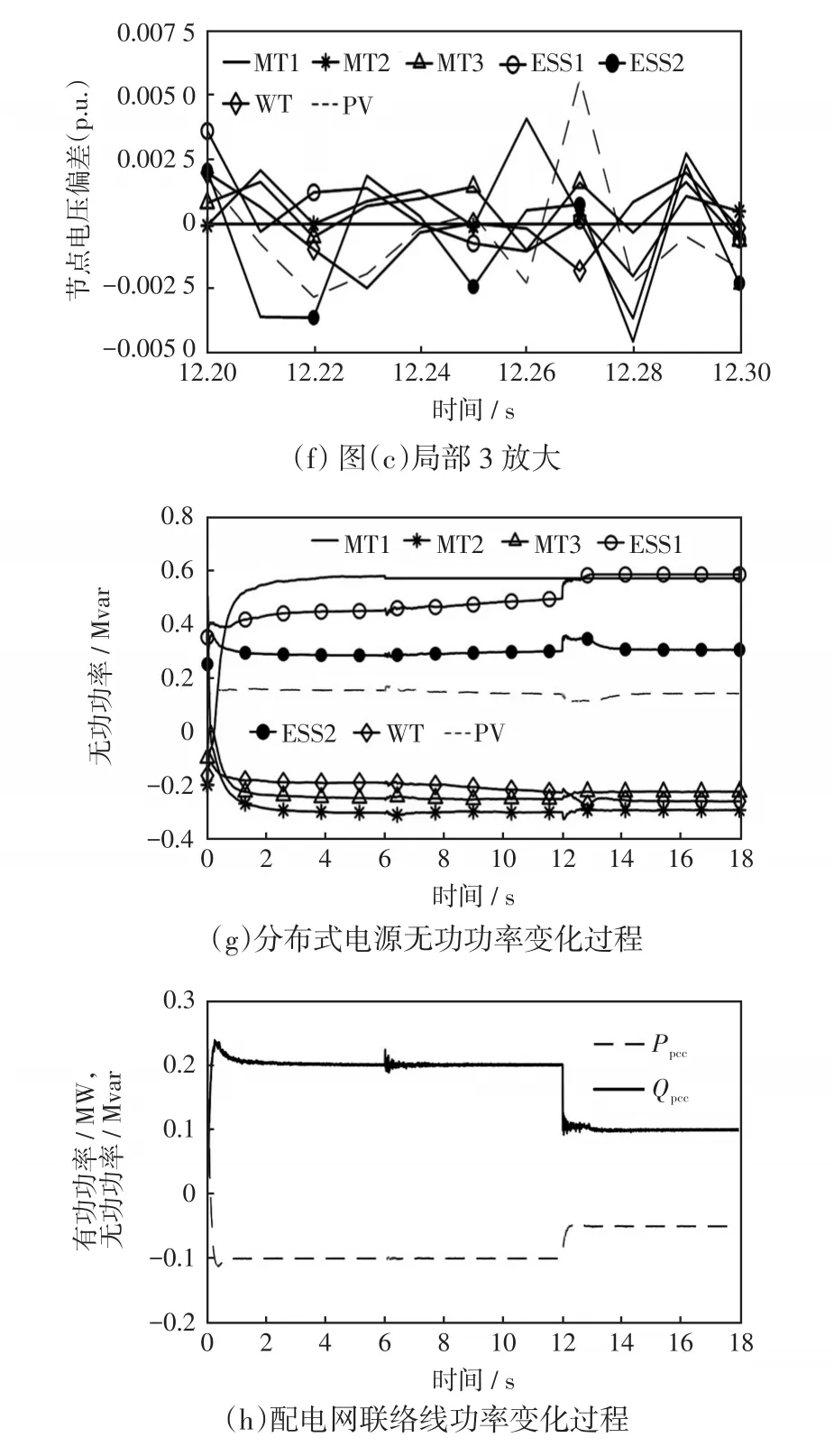
图5 领导节点通信故障情况下多源协同调控策略仿真结果Fig.5 Simulation results of multi-source coordinated control strategy in the case of communication failure at leader node
综上,该多源协同调控策略在应对通信故障的情况有很好的鲁棒性,能够有效地保证对主动配电网联络线功率的可靠追踪。
5 结论
针对非理想通信环境下含多种分布式电源主动配电网的安全经济运行,本文提出了一种结合集中式通信结构、考虑各种分布式电源功率特性、基于改进一致性算法的多源协同调控策略。通过算例验证,结论如下。
(1)根据通信时延以及节点连通度改进一致性的状态转移矩阵,能够加快一致性算法的收敛速度,有效减小非理想通信环境的影响。
(2)在Leader-Follower一致性算法的领导节点牵引控制项中引入积分控制项,能够使牵引控制项的收敛误差明显减小。
(3)结合集中式通信结构的变结构多源协同调控策略能够实时响应配电网功率变化,对各分布式电源的出力进行实时动态调整,保证了配电网功率平衡,实现了配电网的安全、经济运行。
本文的一致性算法控制模型仅考虑了配电网的功率平衡约束、分布式电源出力上、下限约束等,未来将进一步研究考虑潮流、节点电压等网络约束的配电网多源协同优化运行方法。
