执行器约束下基于数据驱动的参数化前馈控制器设计

杨亮亮,张 晖,张 华,鲁文其

(浙江理工大学机械与自动控制学院,浙江杭州 310018)

1 引言

在高速高精度运动控制中,一般采用反馈加前馈的二自由度复合控制策略[1–2].其中反馈控制器用来保证系统的稳定性和对扰动及参数摄动的鲁棒性,前馈控制器用以提高系统响应速度以及轨迹跟踪性能[3–5].常见的前馈控制方法有两种,一种是基于前馈力注入的控制方法;另外一种是基于模型的前馈控制.基于前馈力注入的前馈控制方法一般通过最优化方法获取最优前馈力后将其注入到控制系统中以获得最优控制性能,但是由于最优前馈力是轨迹的泛函,当轨迹发生变化时,需要重新计算最优前馈力,否则会导致控制性能恶化[6–9],因此,基于前馈力注入的设计方法一般用于固定轨迹的重复运动场合.而基于模型的前馈控制器设计方法其前馈控制器一般为被控对象模型的逆,因此,不会因为运动轨迹的变化而导致性能恶化,但是当对象为非最小相位系统时,其模型逆是不稳定的,基于该模型逆设计的前馈控制器会导致前馈力过大超出执行器输出范围[1–2,7,10–11].针对这一问题,Zou等[10,12]提出了有限时间预览的稳定逆的方法,但是该方法不仅要通过辨识方法获取被控对象模型,对于复杂系统模型建立难度较大,而且稳定逆逼近设计的方法相对比较复杂且对预览时间有要求.

另一种基于模型的前馈控制方法是将前馈控制器参数化,得到的最优参数与系统的模型有关,同样不会随着轨迹的变化而变化,也能实现良好的跟踪性能[13–20].该方法避免了繁琐的模型辨识过程,并且该前馈控制器是一个稳定的有限脉冲响应滤波器[21–22].Boeren等[21–23]提出了引入基函数方法对前馈控制器参数化[24–25].文献[21]采用基函数对前馈控制器进行参数化,通过最小二乘法进行最优参数辨识,并运用在两质量运动模型上,验证了前馈参数化算法能够实现不依赖参数模型而实现较高的轨迹跟踪性能,但是当被控对象非单位分子时,算法性能会恶化.文献[23]中改进了参数化前馈控制算法,加入了输入整形滤波器,并对整形滤波器以及前馈控制器进行参数化,然后再经过最小二乘法进行参数辨识,得到参数最优值,适用于被控对象非单位分子的情况.文献[26]在输入整形与前馈参数化的基础上,通过梯度下降法求解最优前馈控制器,并运用于伺服控制平台,实现良好的变轨迹跟踪性能.这些方法中采用最小二乘法或梯度法进行最优参数辨识,其中最小二乘法的性能指标只是误差的二范数,虽能够通过一次迭代得到最优参数,但是对于执行器受约束的情况,可能会导致得到的最优前馈力超出了执行器的输出范围,同样,梯度法的性能指标也只是误差的二范数,其只能限制误差随辨识参数的变化快慢,未能考虑执行器输出受限时,前馈力超出其输出范围的问题.

因此,本文在文献[23]的基础上提出一种改进的前馈算法,改进算法的最优控制目标函数考虑了系统的误差,控制信号的迭代变化以及控制信号能量大小,通过数据驱动的方法逐步迭代达到参数最优值,从而适用在执行器受约束情况下的非重复性轨迹跟踪任务,使运动控制系统在执行器受约束时能够实现对非重复性轨迹的良好跟踪性能.

本文结构如下: 第2节问题定义中介绍了参数化输入整形滤波器与前馈控制器的前馈控制,并分析了现有控制方法辨识参数无约束造成的影响;第3节对改进算法的输入整形滤波器与前馈控制器的参数辨识;第4节对改进算法与现有算法进行了比较,并对改进算法的参数收敛性进行了分析;第5节通过仿真与实验对算法进行验证,并对仿真与实验结果进行分析;第6节进行总结.

2 问题定义

2.1 参数化输入整形滤波器与前馈控制器

参数化输入整形滤波器与前馈控制器控制系统框架如图1所示.控制系统中输入整形滤波器Ty对参考轨迹进行整形,前馈控制器Tff改善伺服性能,反馈控制器Cfb保证系统闭环稳定,被控对象P为离散单输入单输出线性时不变系统.系统传递函数可写为

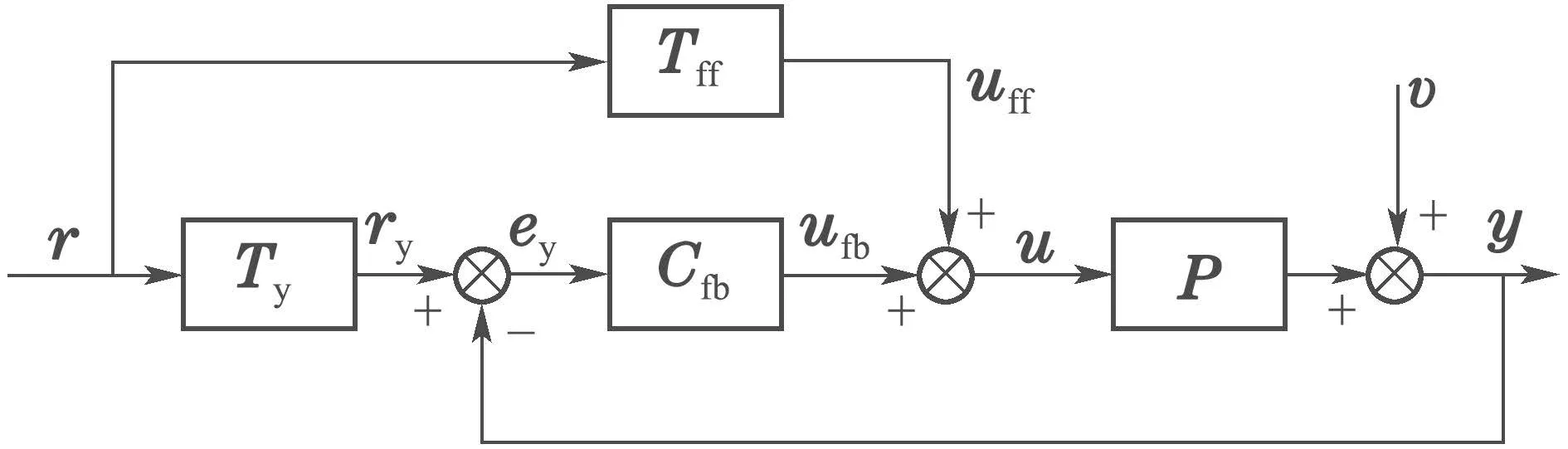
图1 控制系统框架Fig.1 Control system framework

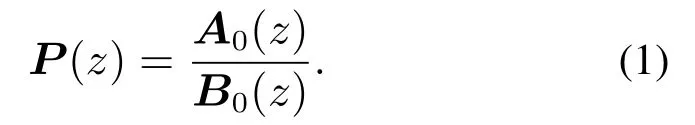
此外,r为事先规划好的输入轨迹信号,ry为整形输入轨迹信号,y为输出信号,ey为整形输入信号与输出信号的误差,uff为前馈控制信号,ufb为反馈控制信号,u为被控对象的控制信号,v为干扰信号,其中规定敏感函数为T=CfbTy+Tff,系统敏感函数为S=(1+P Cfb)−1.

参考输入轨迹为S型点到点轨迹[27],如图2所示.当t ∈[t1,t2]时,为执行段;当t ∈[t2,t3]时,为稳定段,其中t1为运动起始时刻,t2为轨迹达到终点时刻,t3为轨迹达到终点位置后经过一段时间后的运动稳定时刻.

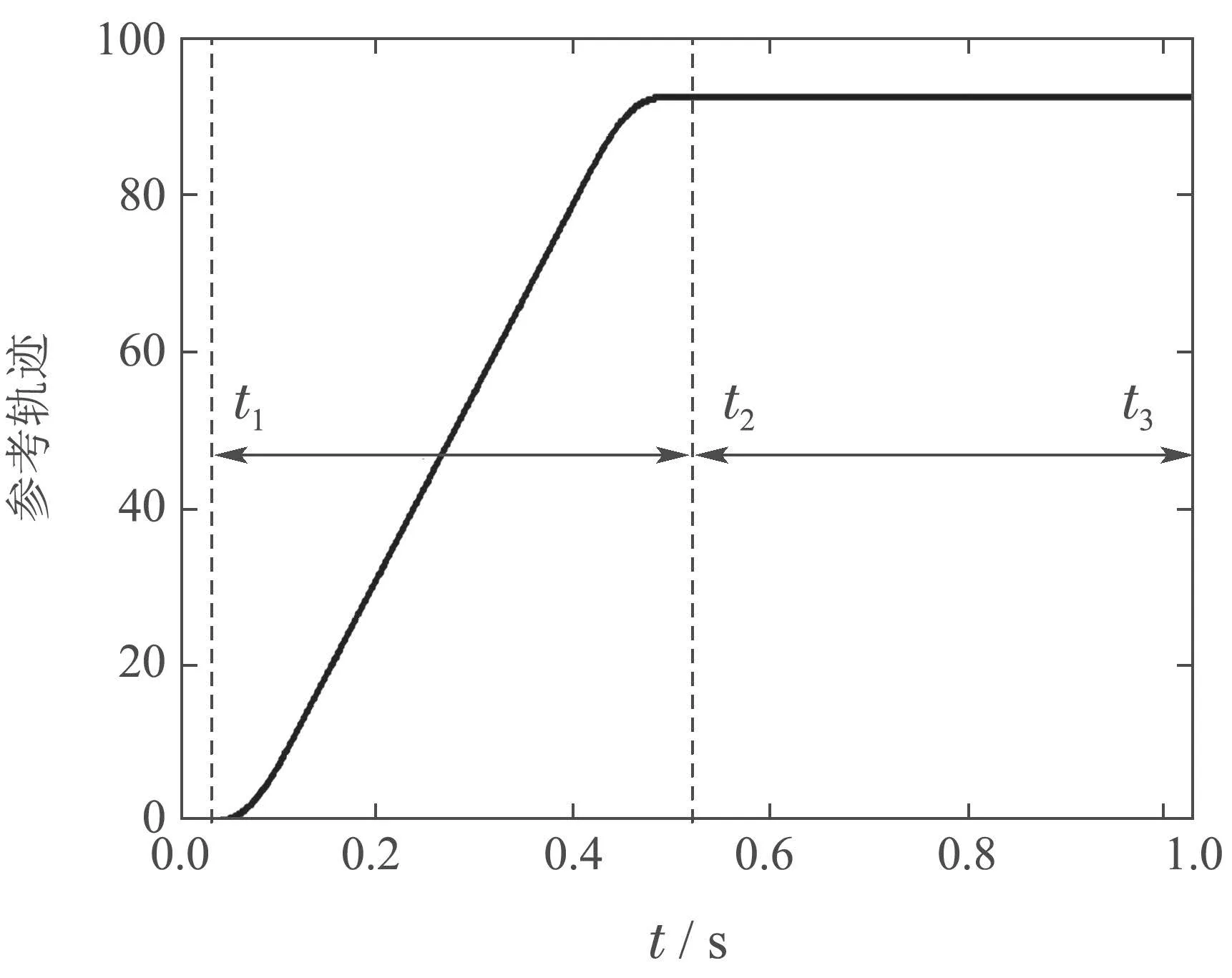
图2 S型点到点参考轨迹Fig.2 S-shaped point-to-point reference trajectory

通过引入基函数将输入整形滤波器Ty和前馈控制器Tff参数化为

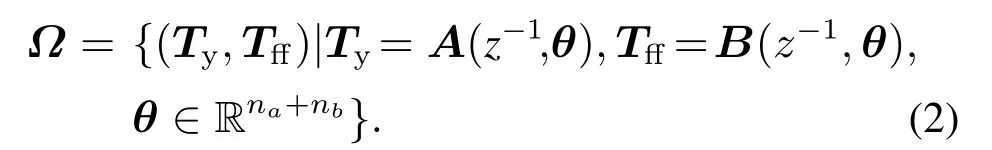
式中:

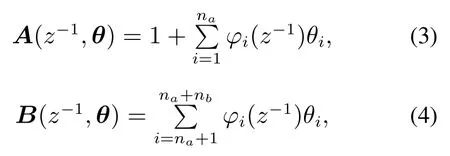
其中:A(z−1,θ),B(z−1,θ)分别为输入整形滤波器和前馈控制器的参数化多项式,θ为参数化基函数多项式要辨识的参数,na,nb为组成Ty和Tff的基函数的个数,Ts为采样时间.基函数φi(z−1)可将输入轨迹分解为各阶导数,例如在A(z−1,θ)中的加速度基函数φ2(z−1)可表示为

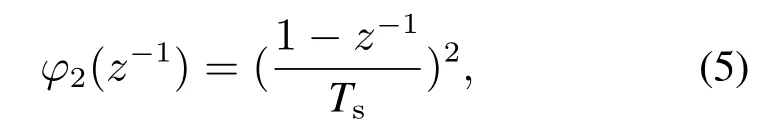
对应的参数θ2为系统质量.

为了简化符号的表达,辨识参数和基函数向量形式表示为

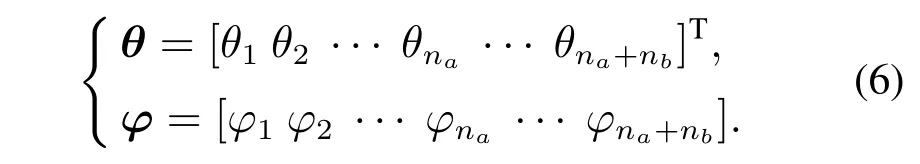
在图1的控制框架中,第j+1次输入整形滤波器和前馈控制器的更新公式为

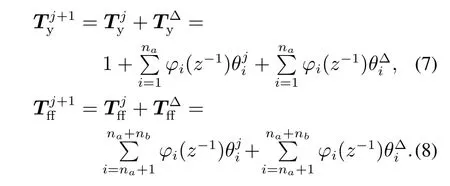
文献[22–23,26,28–29]中,为了使稳定段误差e最小,目标函数均定义为

由图1可知ry=Tyr,图2中在稳定段时Ty|z=1=1,此时ry=r,但执行段有一段延时,延时时长等于Ty中基函数的个数na.故当t ∈[t2+na,t3]时

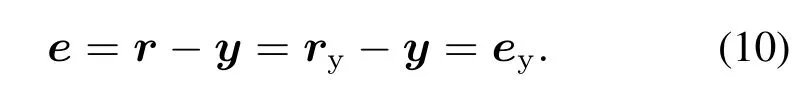
因此在稳定段目标函数J可写为

由图1可知

2.2 参数化前馈辨识参数无约束的影响

在文献[21,23]中,根据式(11)通过最小二乘法获得辨识参数的变化量θ∆为

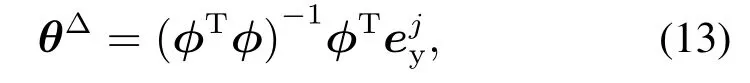
其中

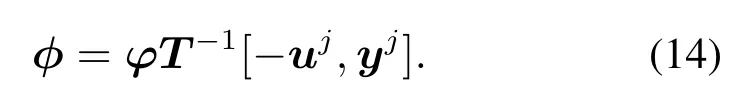
由式(13)辨识参数θ的变化量θ∆是无约束的,能够使辨识参数θ一次得到最优值.由图1,式(7)–(8)可知,当θ∆变化量过大可能导致前馈控制信号uff过大,从而造成控制信号u过大,对于执行器受约束的系统,控制信号过大会造成超出执行器输出范围而导致性能恶化.

因此,一方面为了控制θ变化步长,另一方面为了防止控制信号u输出过大超出执行器的输出范围,本文引入新的目标性能函数式(15),对控制信号u和控制信号变化量∆u进行约束,从而达到对辨识参数的约束.

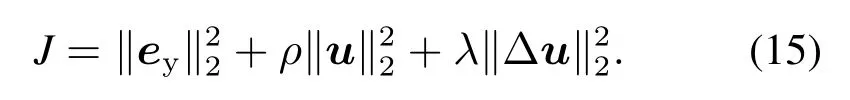
3 改进算法的参数辨识

迭代控制系统框架如图1所示,在不考虑干扰v的情况下,由第j次迭代测量得到,uj,yj的数据,可得

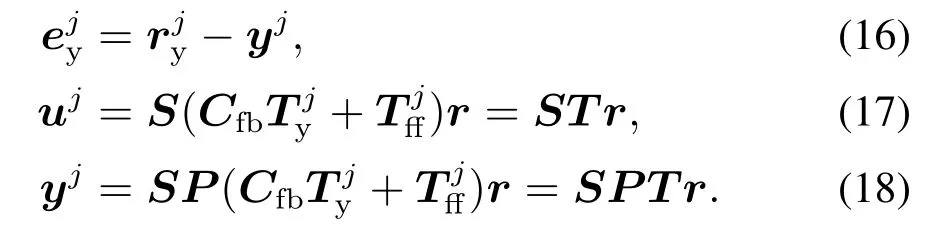
S与SP都跟参数模型有关,为了消除对模型的依赖,根据式(17)–(18)将其转化为基于数据驱动的形式

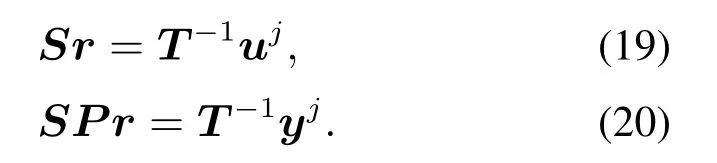
在第j+1次迭代,由上述式子可知

参数的最小二乘估计,就是使目标函数J取极小值的参数θ∆.使上式(32)取得极小值,求J对θ∆的一阶导数,并令其为0,则

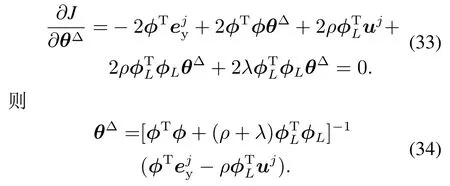
其中:λ为控制信号变化量的约束参数,ρ是控制信号的约束参数.要得到ϕ,ϕL需要求解T−1,如果T−1不稳定,可通过文献[7,10]中方法进行稳定逆逼近,也可参考文献[11]中3种稳定近似逆进行求解,相对于稳定逆逼近,稳定近似逆设计更为简单,本文对于不稳定逆采用稳定近似逆的零相位误差跟踪技术[11,28].

4 改进算法的分析

4.1 改进算法与现有算法的比较

文献[21,23]中最小二乘法辨识参数如式(13)所示,文献[26,29–30]中采用梯度下降法求解最优前馈控制器,通过计算误差ey对辨识参数的梯度值,来求解最优参数值,其迭代学习律为

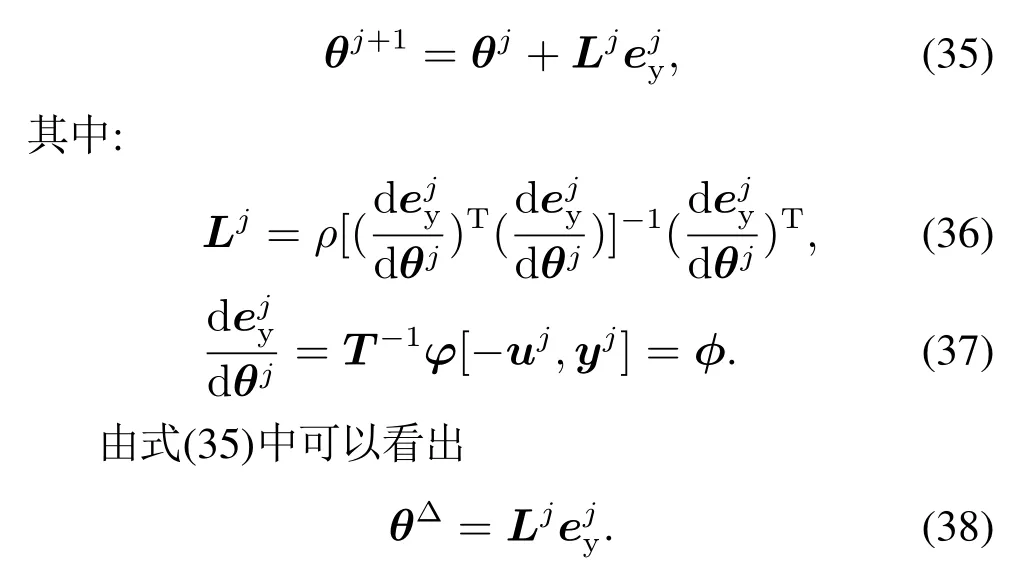
由式(13)(34)(38)可知,现有的最小二乘法是无约束的,未考虑执行器的执行能力,梯度下降法直接通过ρ影响辨识参数变化量θ∆的收敛速度,相对于现有方法,本文算法是针对执行器有约束的情况,通过约束参数λ和ρ直接限制控制信号变化量和控制能量的大小,同时间接的去约束辨识参数变化量θ∆来影响辨识参数θ的收敛速度和收敛值,可以更直接有效防止执行器超出输出范围.

4.2 改进算法的收敛性

输入整形滤波器Ty和前馈控制器Tff均为有限脉冲响应滤波器,而在式(25)中误差ey与有限脉冲响应滤波器参数成线性关系,由文献[15,26]可知误差ey是全局收敛的.由式(25)可知

因此可知,辨识参数θ收敛.

由式(34)可知通过调整约束参数λ和参数ρ,即可约束θ的变化量,当λ=0且ρ=0时,即是退化为式(13)的最小二乘算法.当ρ保持不变,λ取值越大,θ变化量越小,θ收敛到最优值越慢,系统前馈控制信号达到最优值的速度越慢,从而使得误差收敛速度越慢,反之,则收敛速度越快.当λ保持不变,ρ越大,对控制信号约束作用越大,辨识参数变化量越小,误差收敛值越大,反之误差收敛值越小.

4.3 算法实现步骤

综上所述,改进的前馈参数化算法实现步骤如下:

1) 选取θ初值和合适的约束参数λ和ρ.

2) 测量,uj,yj的值.

3) 通过测量值uj,yj计算

6) 不断重复步骤2)–5),直到系统收敛到最优跟踪性能.

5 仿真与实验

5.1 仿真设计与结果

采用MATLAB/Simulink对上述控制算法进行仿真.仿真时参考轨迹采用四阶S型点到点轨迹规划如图3所示.仿真对象模型如下所示:

图3 四阶S型点到点轨迹Fig.3 Fourth-order S-shaped point-to-point trajectory

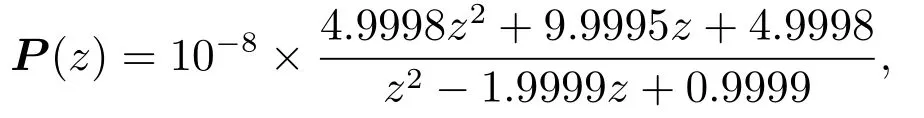
其中采样时间为Ts=5.0×10−4s.

反馈控制器Cfb为

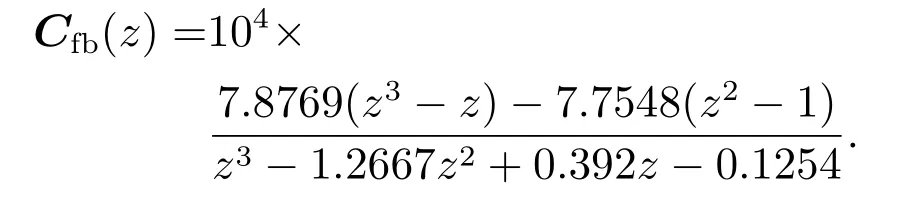
建立输入整形滤波器Ty和前馈制器Tff参数化多项式为

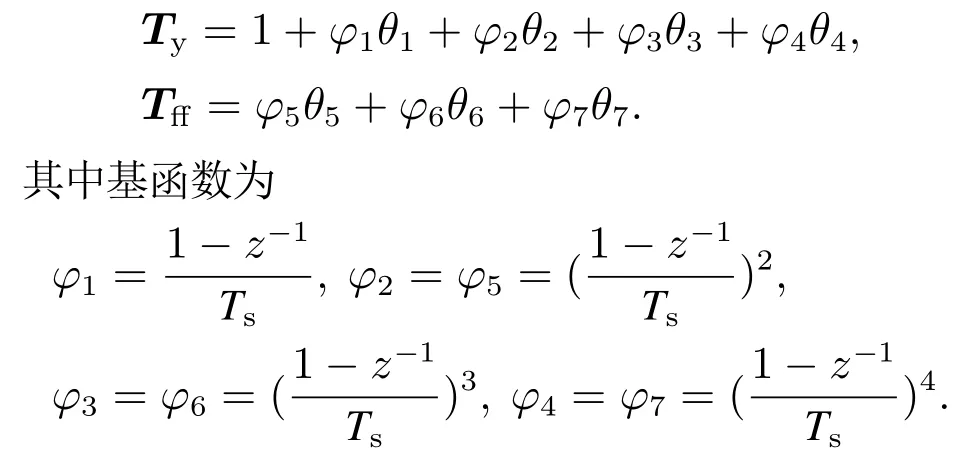
选取初始值θ1=[0 0 0 0 0.1 0 0]T,仿真实验的执行器的输出范围选为−25 N∼25 N.

图4为当约束参数ρ保持不变,只考虑约束参数λ变化时,稳定段误差的二范数随迭代次数变化的曲线.由图可知当ρ=1×10−10时,λ越小,稳定段误差二范数衰减到最优的速度越快.

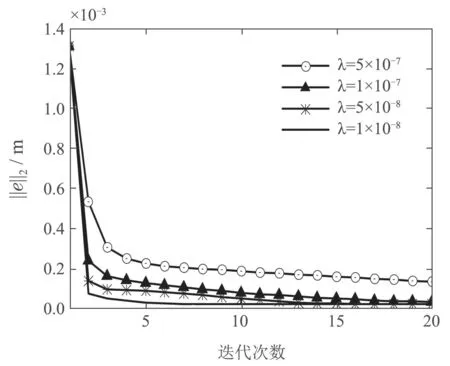
图4 ρ=1×10−10时,约束参数λ对误差二范数的影响曲线Fig.4 Curve of the effect for the constraint parameter λ on the two-norm for the error when ρ=1×10−10

图5为当约束参数λ保持不变时,只考虑约束参数ρ变化时,稳定段误差的二范数随迭代次数变化的曲线.由图可知当λ=1×10−8时,ρ越小,稳定段误差二范数收敛值越小.

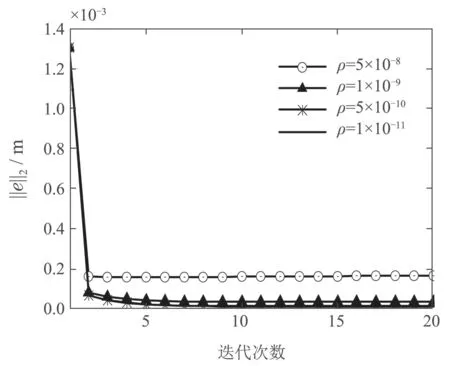
图5 λ=1×10−8时,约束参数ρ 对误差二范数的影响曲线Fig.5 Curve of the effect for the constraint parameter ρ on the two-norm for the error when λ=1×10−8

表1为当约束参数λ保持不变时,不同约束参数ρ下的控制信号最大值,由表可知当λ=1×10−8时,ρ越小控制信号的最大值越大;从上述两个试验可以看出通过约束参数λ可以调整算法的迭代收敛速度,通过约束参数ρ可以调整算法迭代收敛最优值与控制信号最大值的大小.

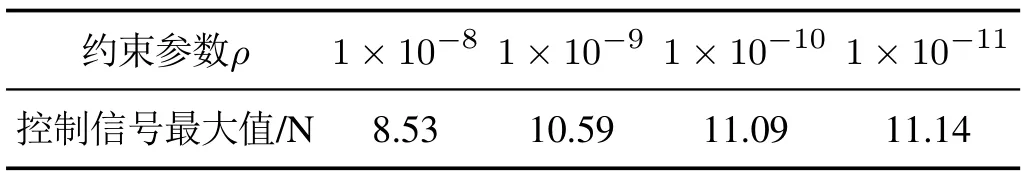
表1 不同约束参数ρ 下的控制信号最大值(λ=1×10−8)Table 1 The maximum value of the control signal with different constraint parametersρ(λ=1×10−8)

因此,执行器受约束的运动控制系统在运用改进算法时,可以根据执行器的输出范围选择合适的约束参数λ和ρ,来调整所提出算法的收敛速度和所需的控制信号.

整段轨迹的迭代前后误差ey如图6所示.图7为迭代前后的稳定段误差e变化曲线.由图可知,第1次迭代时最大轨迹跟踪误差为10−4m量级,第20次迭代时最大轨迹跟踪误差降为10−6m量级.上述仿真实验结果表明改进算法实现了当前约束参数下(λ=1×10−8,ρ=1×10−10)不超出执行器输出范围的轨迹最优跟踪性能.

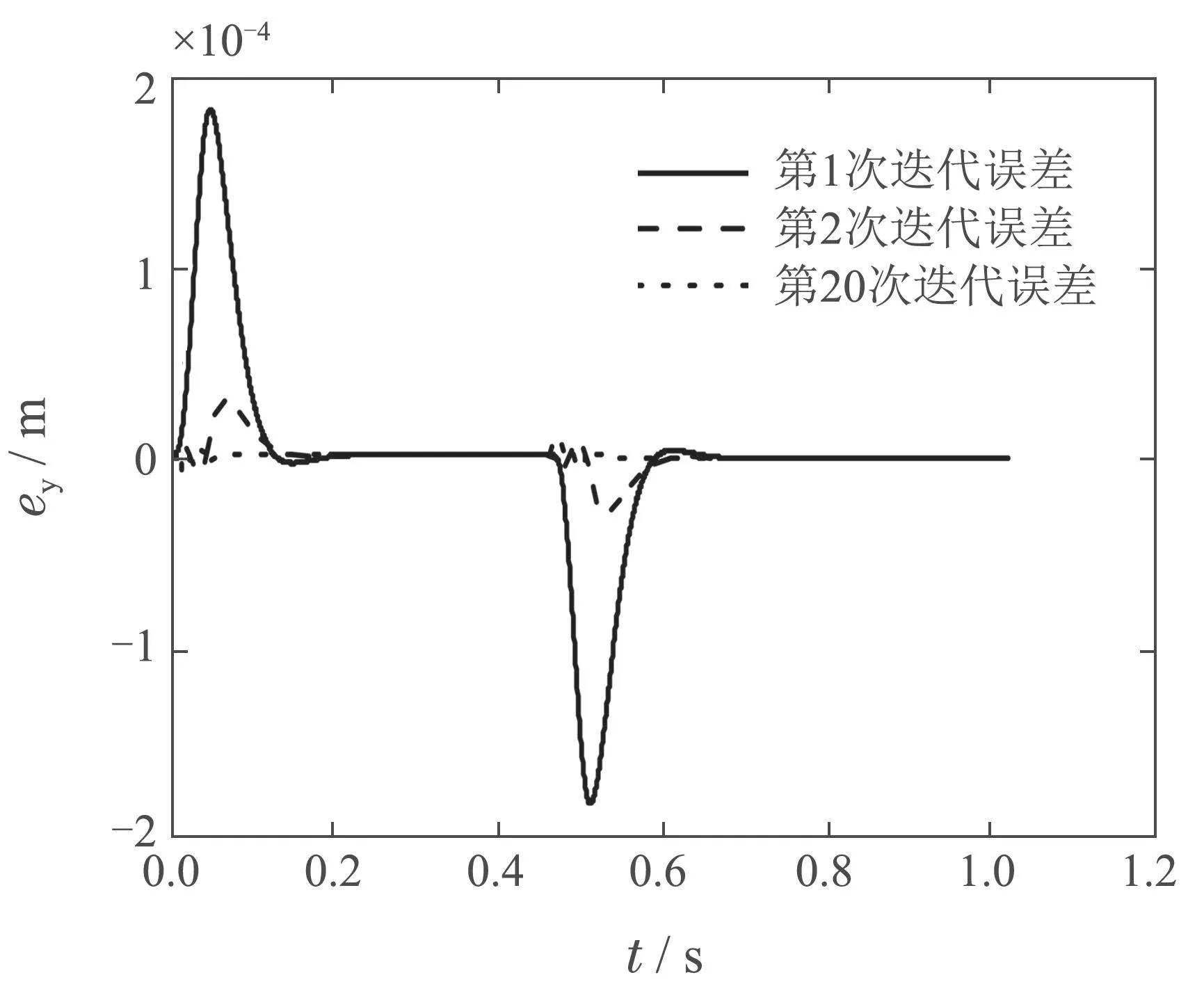
图6 λ=1×10−8,ρ=1×10−10时,迭代误差比较Fig.6 Comparison of iterative errors when λ=1×10−8,ρ=1×10−10

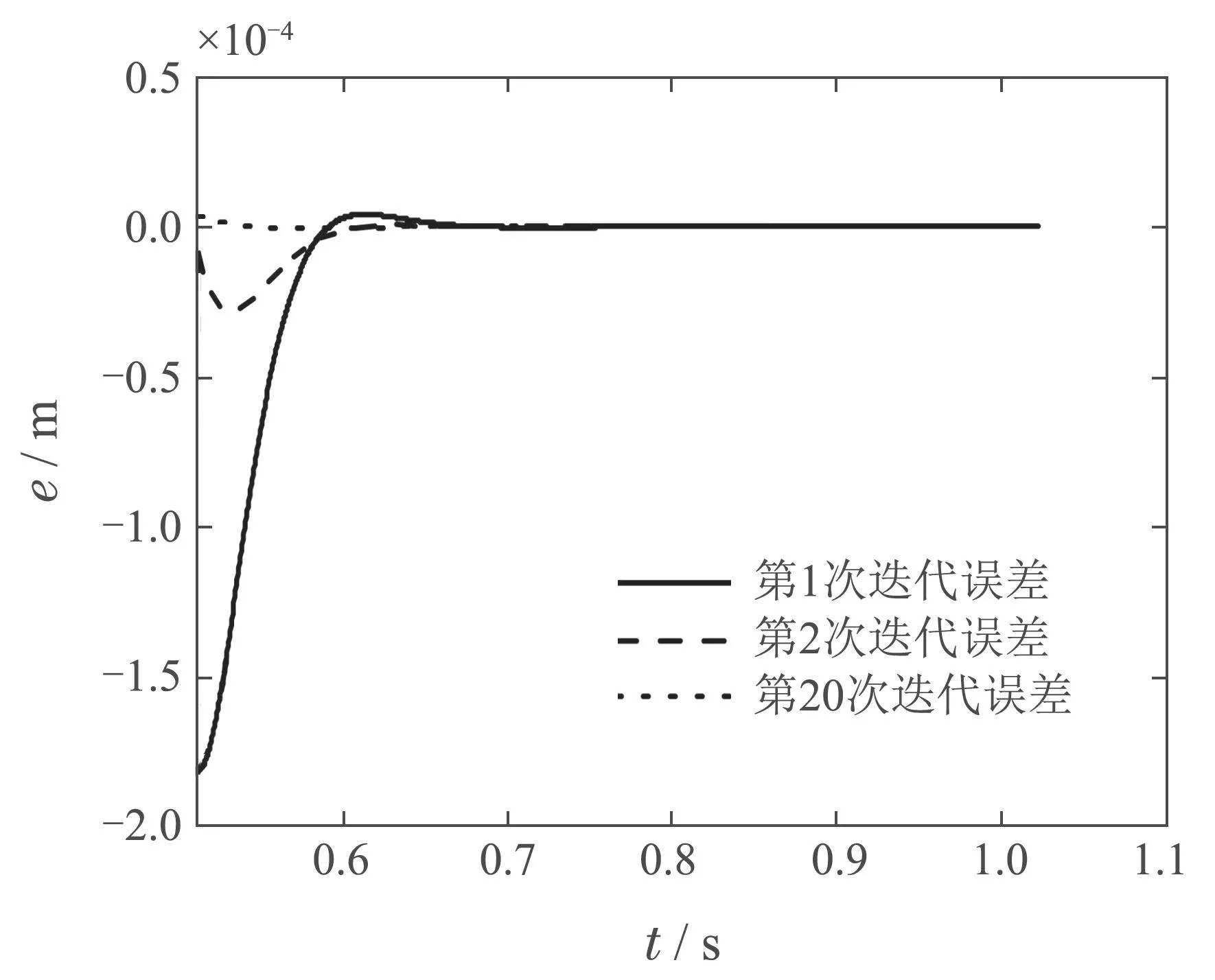
图7 λ=1×10−8,ρ=1×10−10时,稳定段迭代误差比较Fig.7 Comparison of iterative errors in the settling section when λ=1×10−8,ρ=1×10−10

辨识参数θ变化曲线如图8所示,由图可知,辨识参数θ1∼θ7在第7次迭代后收敛到最优值,最优值如表2所示,该结果验证了改进算法辨识参数的收敛性.

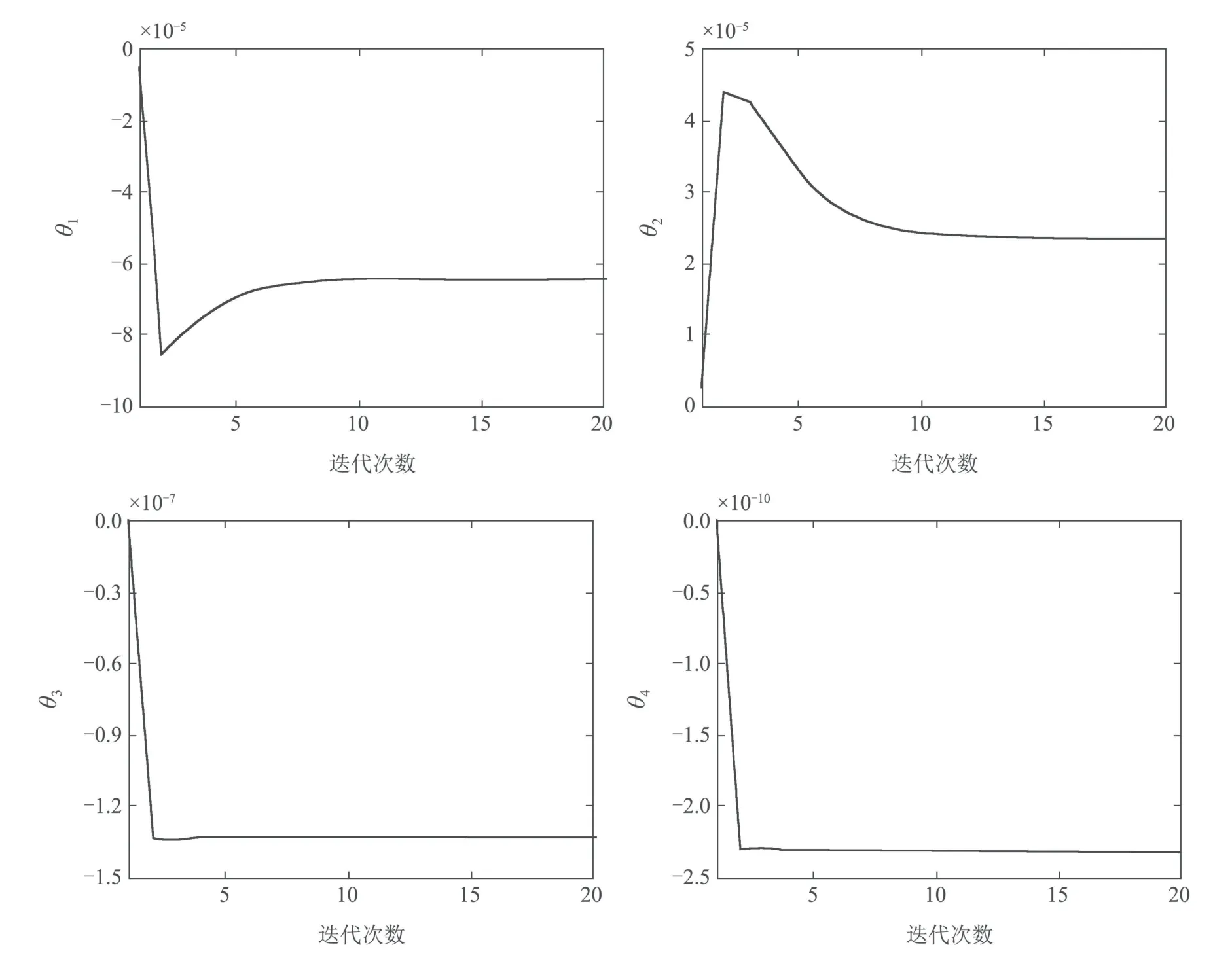
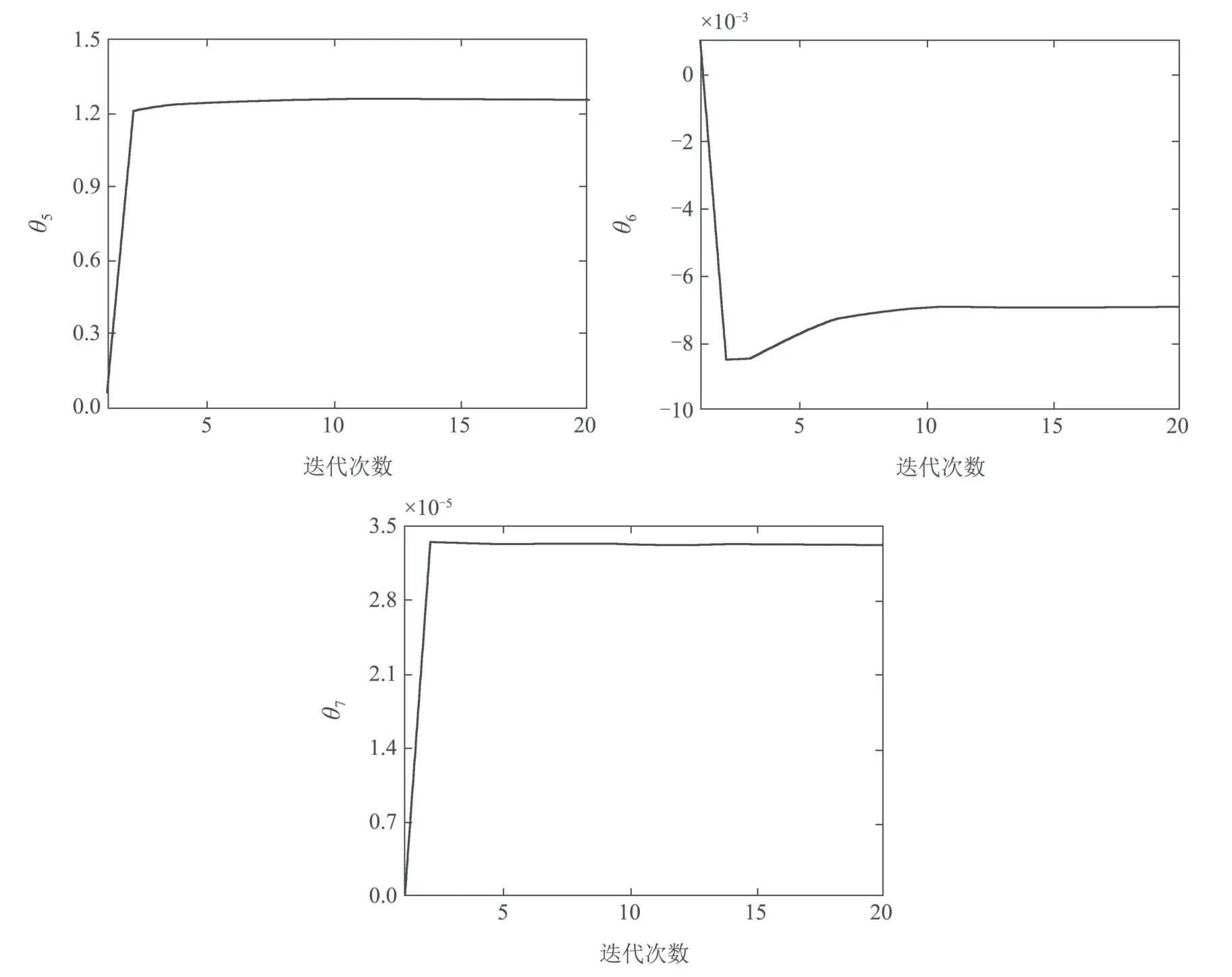
图8 λ=1×10−8,ρ=1×10−10时,辨识参数θ 变化曲线Fig.8 The variation curve of identification parameter θ when λ=1×10−8,ρ=1×10−10

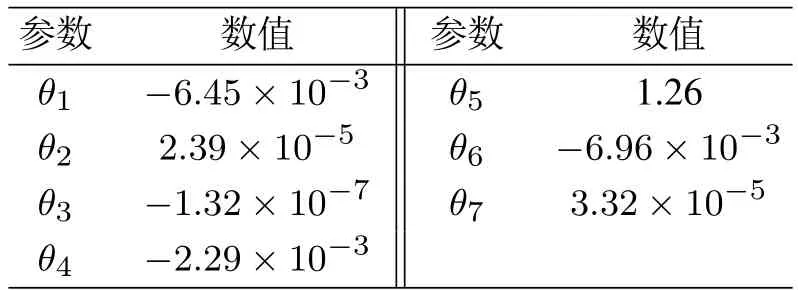
表2 参数θ最优值(λ=1×10−8,ρ=1×10−10)Table 2 The optimal value of the parameter θ(λ=1×10−8,ρ=1×10−10)

5.2 所提出算法与现有算法比较

图9为文献[17]中现有无约束参数的算法(λ=0,ρ=0)与所提出有约束参数的改进算法(挑选λ=1×10−8,ρ=1×10−10)控制信号曲线的比较图.由图可知,在无约束参数算法运行的情况下,控制信号最大值超出执行器输出范围−25 N∼25 N,加入约束后的改进算法控制信号最大值未超出执行器输出范围.

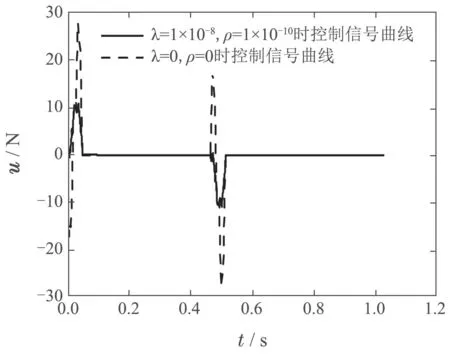
图9 加入约束参数前后的控制信号u的比较Fig.9 Comparison of control signals u before and after adding constraint parameters

5.3 实验验证

本文的实验平台为图10所示两个直线电动机构成的X-Y运动平台,两个直线电动机均采用Baldor公司的LMCF02C-HCO,电动机的连续推力为58 N,峰值推力为173 N,直线电动机的运动位置由GSI公司分辨率为0.5µm的光栅尺测量,读数头型号为MII1600-40.伺服驱动器为Baldor公司的FMH2A03TR-EN23,采用电流控制方式.由于位于上层直线电动机具有相对较低的惯量,为了验证高速高精性能,实际试验时采用下层直线电动机锁死,只对上层直线电动机进行试验.由于电动机的连续推力为58 N,因此为了保证实验的安全性和验证算法的有效性,实验平台的执行器的推力输出范围选为−60 N∼60 N.

图10 直线伺服电机实验平台Fig.10 Linear servo motor experiment platform

实验的反馈控制器采用PID反馈控制,其参数如表3所示.

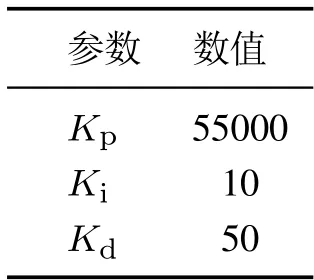
表3 PID参数Table 3 PID parameters

实验采用参考轨迹如图11所示,四阶S型点到点轨迹,伺服采样时间为5×10−4s,迭代运行20次,参数初始值θ1=[0 0 0 0 0.1 0 0]T,输入整形滤波器和前馈控制器参数化多项式与仿真实验一致,实验过程中采集输出轨迹,误差和控制信号数据.

图11 四阶S型点到点参考轨迹Fig.11 Fourth-order S-shaped point-to-point reference trajectory

图12为当约束参数ρ保持不变时,只考虑约束参数λ变化时,稳定段误差的二范数随迭代次数变化的曲线.由图可知当ρ=1×10−6时,λ越小,稳定段误差二范数衰减到最优的速度越快.图13为当约束参数λ保持不变时,只考虑约束参数ρ变化时,稳定段误差的二范数随迭代次数变化的曲线,由图可知当λ=0.001时,ρ越小,稳定段误差二范数的收敛值越小.

图12 ρ=1×10−6时,约束参数λ对误差二范数的影响曲线Fig.12 Curve of the effect for the constraint parameter λ on the two-norm for the error when ρ=1×10−6

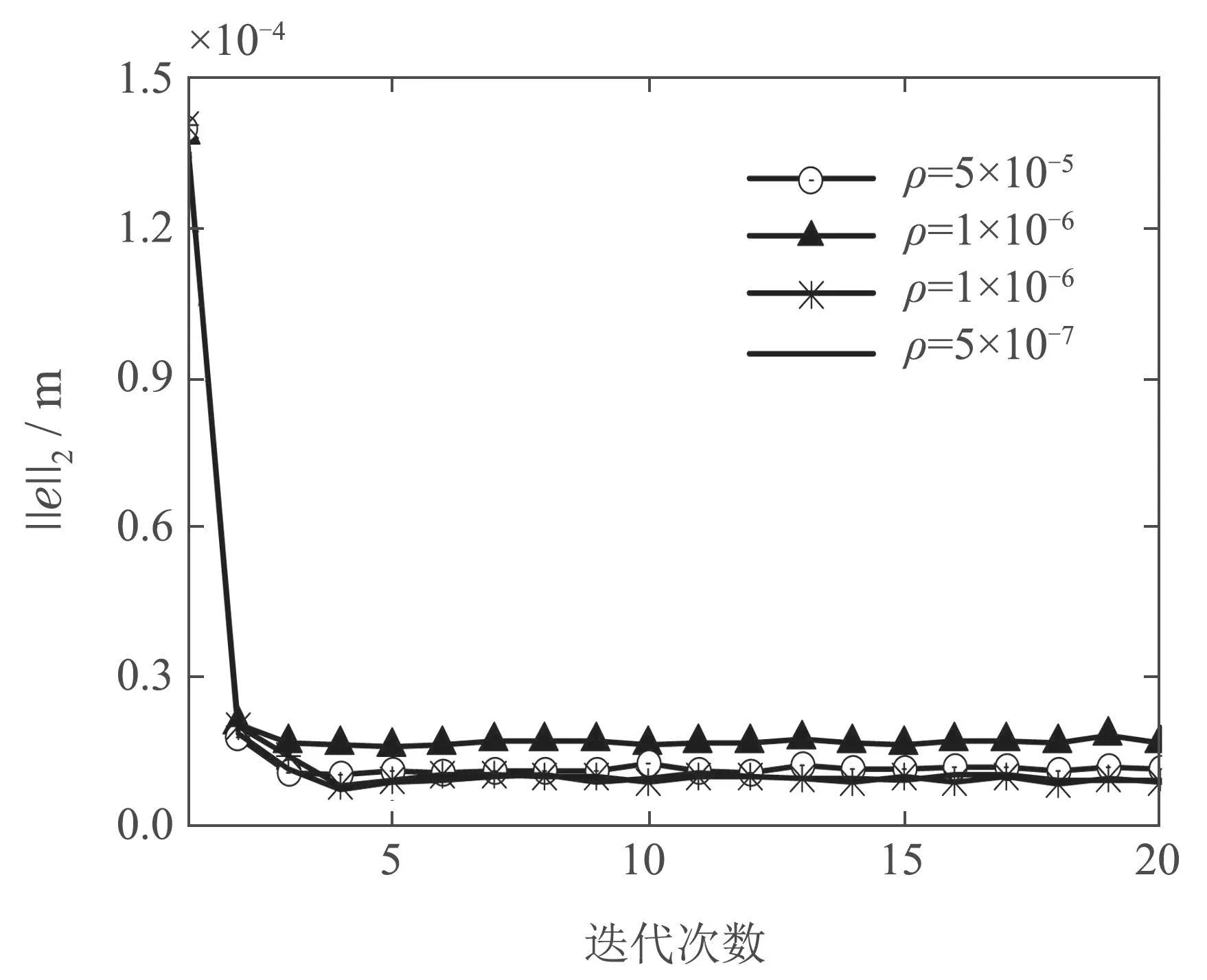
图13 λ=0.001时,约束参数ρ对误差二范数的影响曲线Fig.13 Curve of the effect for the constraint parameter ρ on the two-norm for the error when λ=0.001

表4为当约束参数λ保持不变时,不同约束参数ρ下的控制信号最大值,由表可知当λ=0.001时,ρ越小控制信号的最大值越大.上述实验结果与仿真实验结果一致,表明了算法可以通过约束参数λ调整算法的迭代收敛速度,通过约束参数ρ调整算法迭代收敛最优值与控制信号最大值的大小.

表4 不同约束参数ρ下的控制信号最大值(λ=0.001)Table 4 The maximum value of the control signal with different constraint parameters ρ(λ=0.001)

整段轨迹的迭代前后误差ey如图14所示.图15为稳定段迭代前后的误差e变化曲线,由图可知,实验效果与仿真一致,由第1次、第2 次和第20 次稳定段误差的变化趋势可知,稳定段误差得到了明显的抑制,表明了改进算法能够实现在当前约束参数下(λ=0.001,ρ=1×10−6)不超出执行器输出范围的轨迹最优跟踪性能.

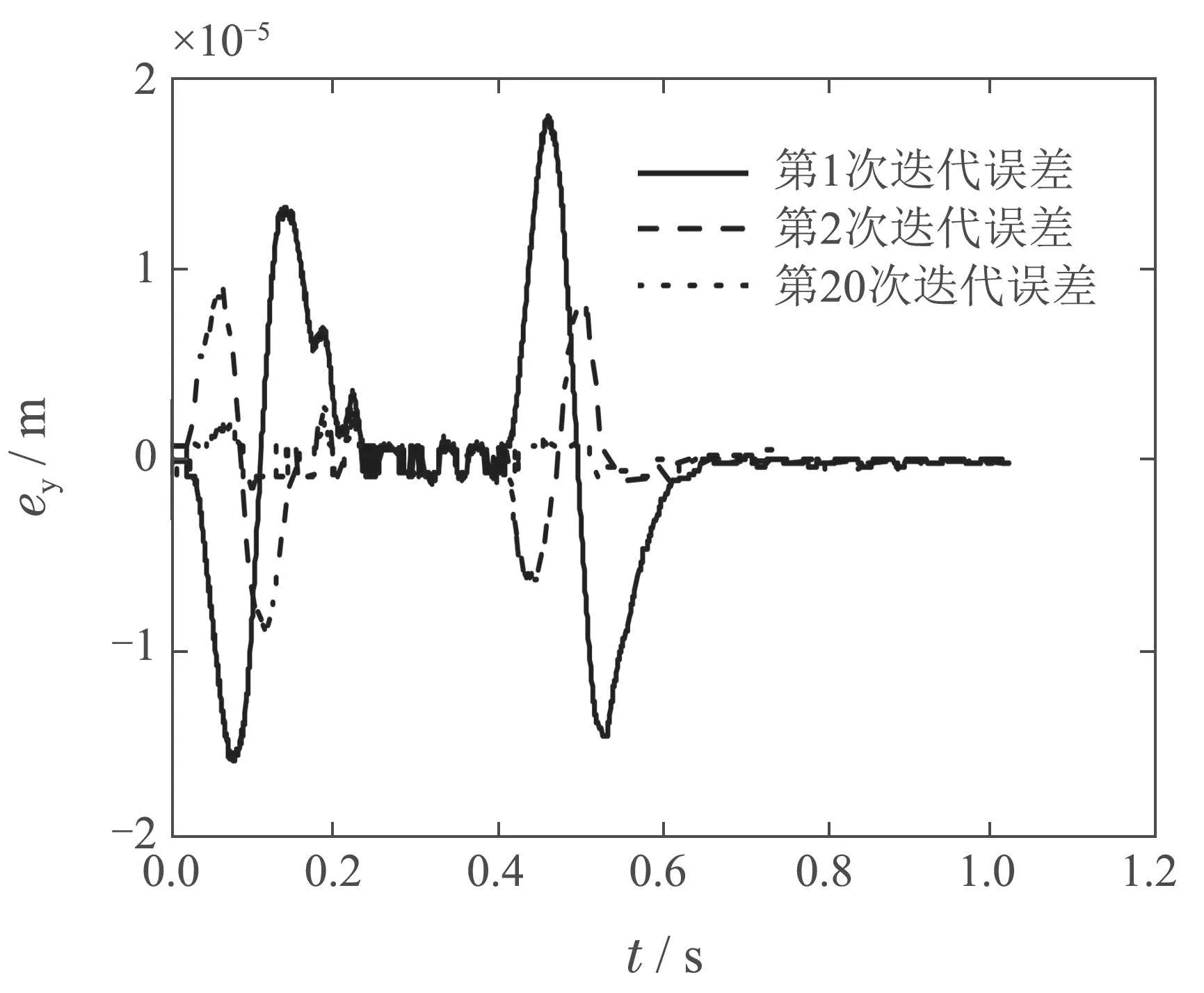
图14 λ=0.001,ρ=1×10−6 时,迭代误差比较Fig.14 Comparison of iterative errors when λ=0.001,ρ=1×10−6

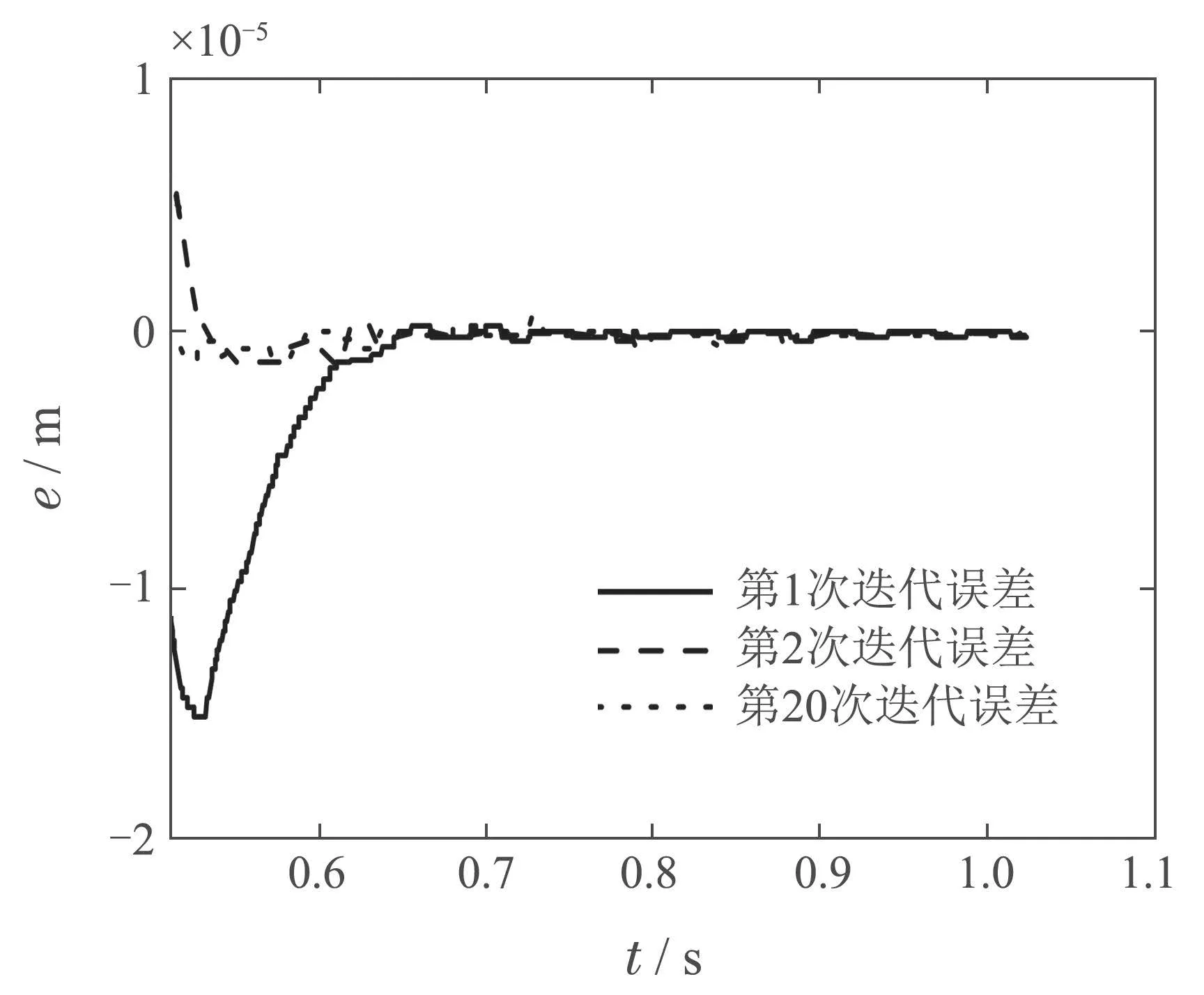
图15 λ=0.001,ρ=1×10−6 时,稳定段迭代误差比较Fig.15 Comparison of iterative errors in the settling section when λ=0.001,ρ=1×10−6

辨识参数θ变化曲线,如图16所示,由图可知,辨识参数θ1∼θ7在第5次迭代收敛到最优值,辨识参数的最优值如表5所示.实验结果进一步验证了改进算法辨识参数的收敛性.

表5 参数θ 最优值(λ=0.001,ρ=1×10−6)Table 5 The optimal value of the parameter θ(λ=0.001,ρ=1×10−6)

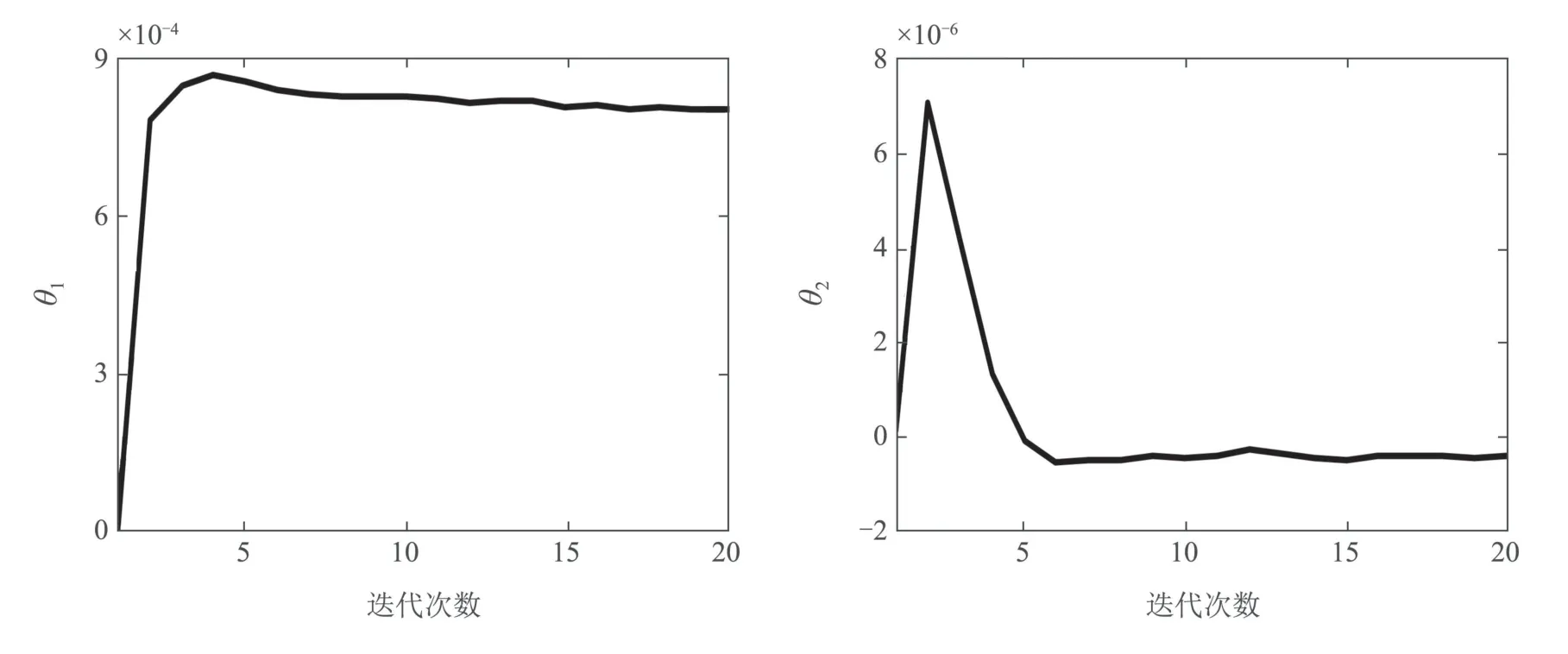
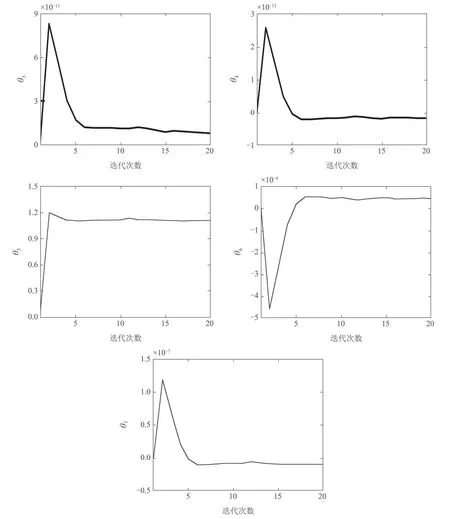
图16 λ=0.001,ρ=1×10−6 时,辨识参数θ变化曲线Fig.16 The variation curve of identification parameter θ when λ=0.001,ρ=1×10−6

5.4 非重复性轨迹实验

为了验证改进算法在执行器约束下对非重复性轨迹的性能,实验选用的参考轨迹如图17所示.非重复性轨迹实验,前10次迭代采用图中参考轨迹1,后10次迭代采用参考轨迹2.该实验采用与上述实验同样的控制结构、伺服采样时间和初值,约束参数选为λ=0.001,ρ=1×10−6.

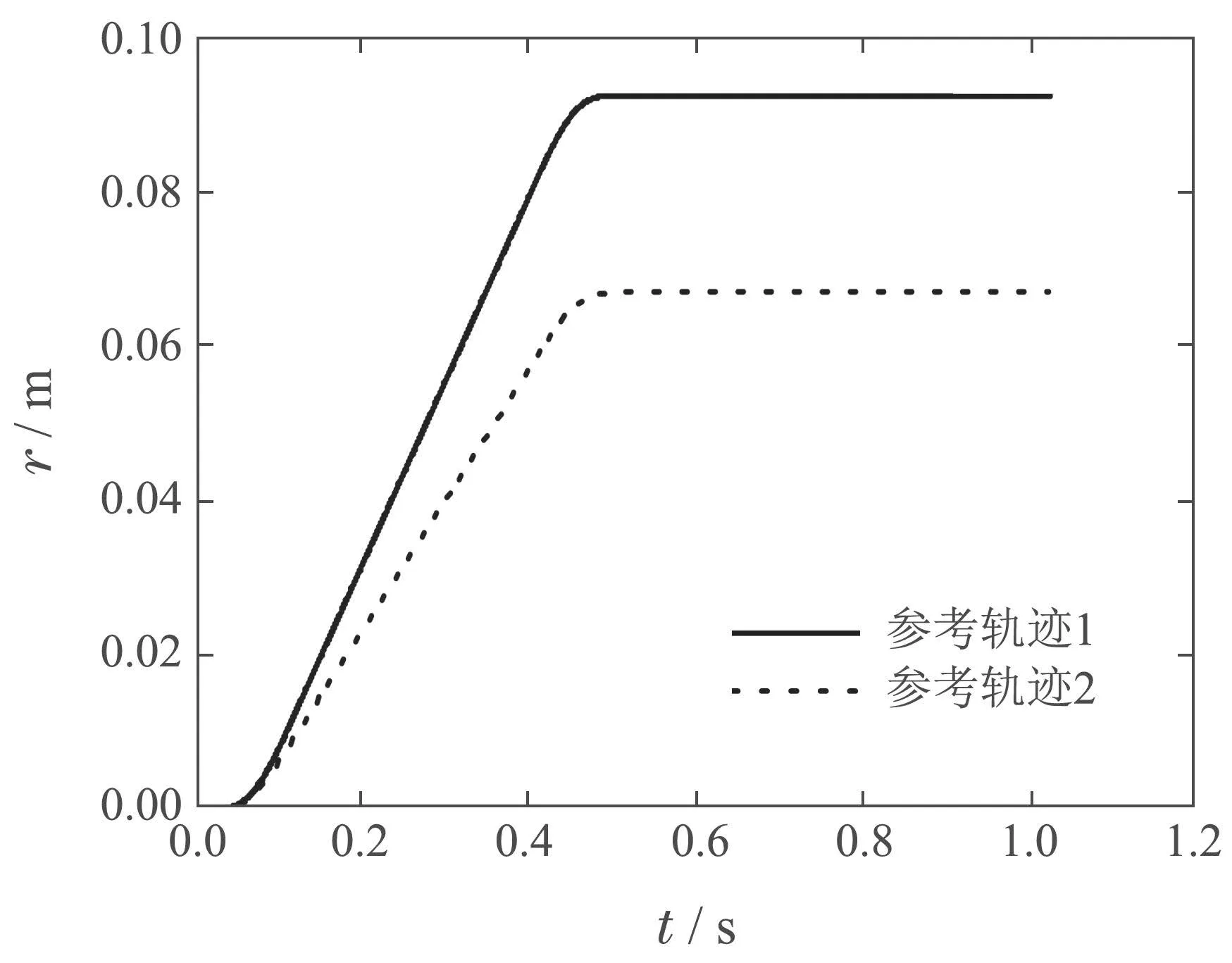
图17 非重复性轨迹实验中四阶S型点到点参考轨迹1和2Fig.17 Fourth-order S-shaped point-to-point reference trajectories 1 and 2 in non-repetitive trajectory experiment

非重复性轨迹实验中,稳定段误差二范数变化曲线如图18所示,前10次迭代稳定段误差二范数收敛到最优值,在第11次迭代轨迹发生变化时,稳定段误差二范数的值略微上升,但与轨迹1性能差别不大,在经过一次迭代后又收敛到最优值,与轨迹1时的最优性能一致.

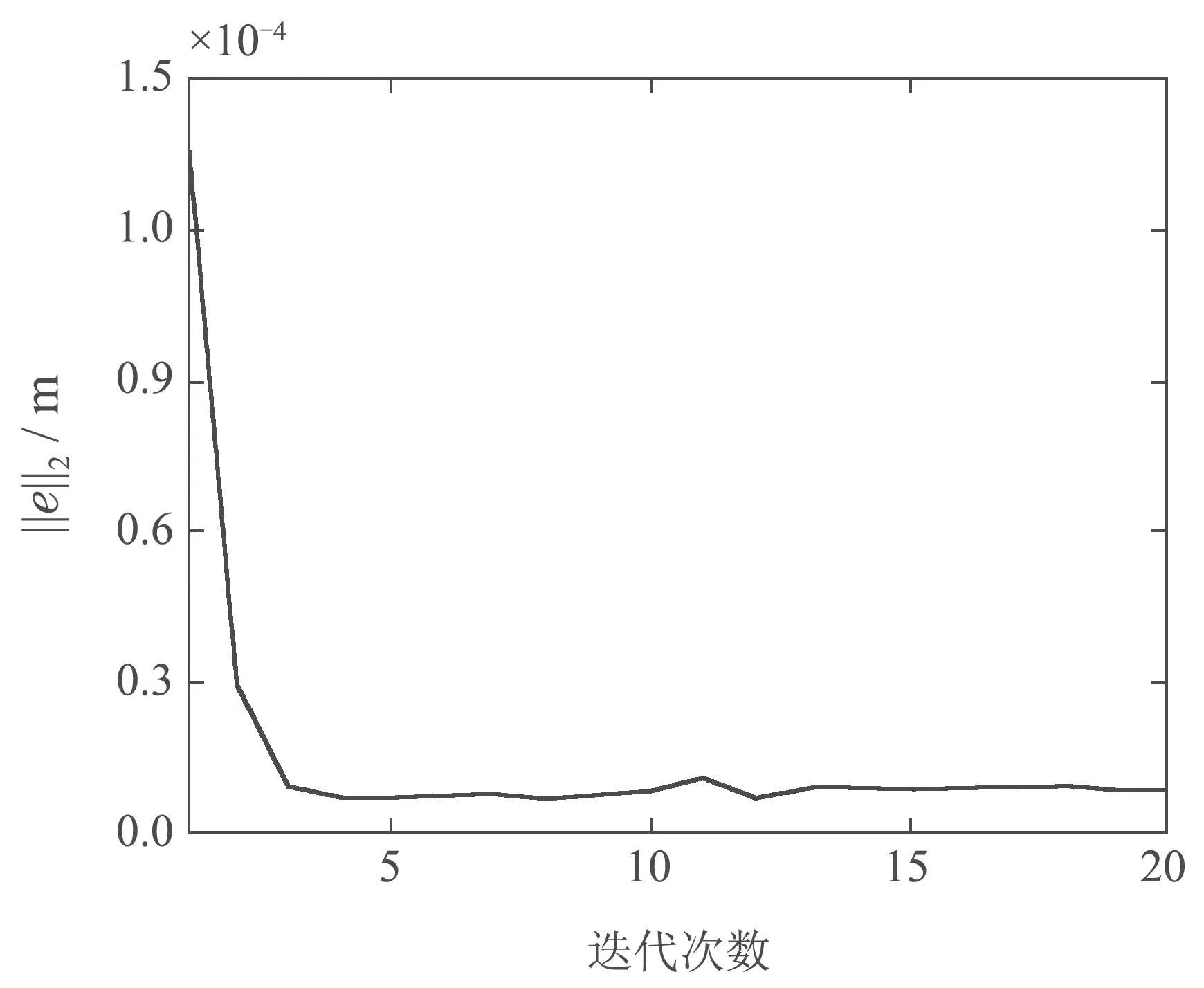
图18 非重复性轨迹实验误差二范数的变化曲线Fig.18 The variation curve of the two-norm error for the non-repetitive trajectory experiment

非重复性点到点轨迹运动实验中,运行轨迹1达到收敛时的控制信号曲线如图19所示,运行轨迹2 达到收敛时的控制信号曲线如图20所示.由图可知,两条轨迹运行达到收敛时的控制信号最大值均为未超出执行器的输出范围.非重复性轨迹实验结果表明了改进算法在执行器约束下对非重复性点到点轨迹具有一定的鲁棒性.

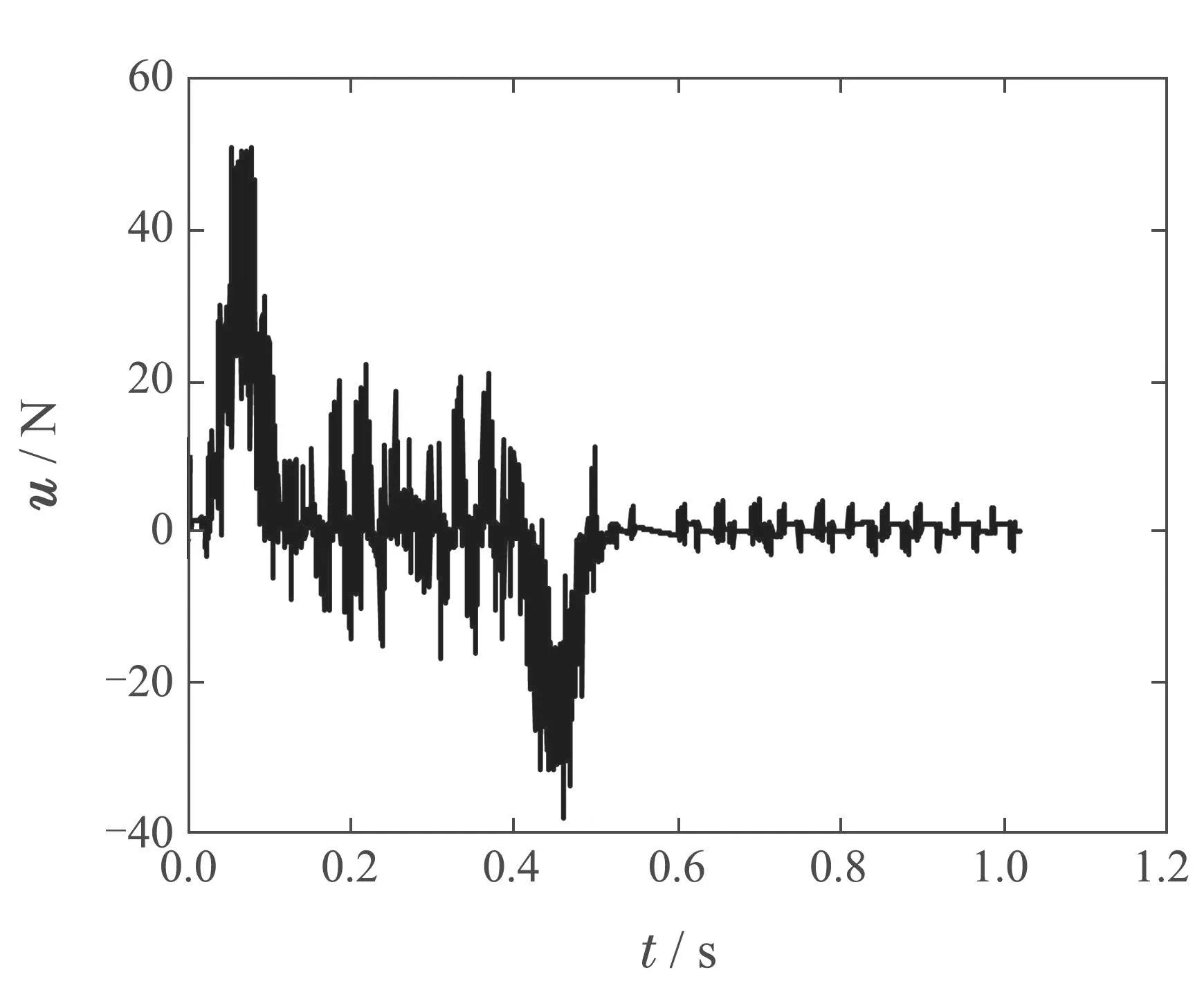
图19 运行轨迹1时的控制信号u曲线Fig.19 Control signal u curve when running trajectory 1

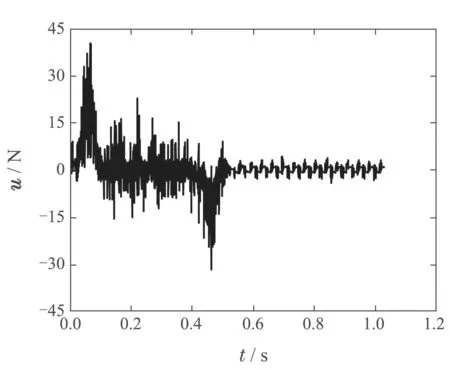
图20 运行轨迹2时的控制信号u曲线Fig.20 Control signal u curve when running trajectory 2

6 总结

为了实现在执行器受约束情况下非重复性点到点轨迹的最优跟踪,本文提出了一种在执行器约束情况下参数化输入整形滤波器和前馈控制器的数据驱动控制算法.算法运用了数据驱动的方法进行迭代更新辨识最优参数,不依赖被控对象数学模型,并通过限制控制信号变化量和控制能量来达到对辨识参数的约束,从而满足在执行器约束条件下实现非重复性轨迹跟踪,并且跟踪误差和辨识参数收敛到最优值.通过仿真和实验验证: 本文算法能够实现在执行器约束下对点到点轨迹的最优跟踪性能,并且对非重复性点到点轨迹具有一定的鲁棒性.