基于转子分段的永磁电机齿槽转矩抑制方法研究

姜富宽

(驻马店技师学院，河南 驻马店 463000)

0 引 言

磁通反向电机永磁体放在定子齿表面，安装方便，转子是简单的磁阻结构，适应于高速和高温运行，同时其又具有功率密度高、容错性好、调速性能好、动态响应快、效率高等性能特点，因此磁通反向电机适合于多种调速运行场合，如新能源汽车等。此外，磁通反向电机具有磁场增速特性，因此磁通反向电机也适用于要求低速大转矩的直驱场合，例如新能源发电和长轨道直线直驱场合[1]。然而，磁通反向电机控制系统的转矩脉动相对比较严重，较大的转矩脉动势必会降低整个系统的控制精度，进而影响整体的性能，此外，转矩脉动也会导致电机系统的振动和噪声。因此，有必要对其进行研究和抑制。

由于磁通反向电机的磁钢直接放在气隙之中，且转子为磁阻结构，因此该电机的齿槽转矩相对比较大，这也是引起该类电机转矩脉动的主要原因之一。事实上，国内外学者针对磁通反向永磁电机齿槽转矩及其抑制技术的探索做了许多的研究工作，包括齿槽转矩建模、齿槽转矩优化以及从控制角度进行抑制等[2-8]。

在齿槽转矩建模方面，其中文献[2]基于磁共能法及磁势-磁导模型，首先推导了磁通反向永磁电机齿槽转矩解析模型，并在此模型的基础上，分析了电机参数对齿槽转矩波形及谐波分布的影响，提出了优选定、转子齿宽以降低齿槽转矩的方法。文献[3]则基于有限元法，建立了电机的仿真模型。一般而言，解析法常常忽略磁饱和以及漏磁等因素，因此，精度相对较低，但是其能反应齿槽转矩与电机尺寸参数之间的关系，对齿槽转矩的抑制措施提供指导意义。

而在齿槽转矩优化方面，文献[3]以电机输出转矩最大化和齿槽转矩最小化为优化目标，采用田口法对选定的优化参数设计了正交试验，分析了各优化参数对优化目标的影响，从而确定了优化方案。研究结果表明，所采用的方法确实不仅能减小齿槽转矩还能提高输出转矩。此外，文献[4]将磁通反向电机运用于直线旋转电机领域，通过在三维磁路结构中增加可变磁阻单元，建立了磁通反向直线旋转永磁电机的三维非线性等效磁路模型。文献[5]对比研究了4种具有“consequent pole”结构的磁通反向电机电磁性能，分析了各自的工作原理和气隙磁场谐波特性，从而筛选出具有较大转矩输出的电机拓扑结构。

在电机控制方面，文献[6]从控制的角度出发，提出了一种基于电压矢量优化的模型预测转矩控制方法，降低了磁通反向电机控制系统的转矩脉动。此外，在转矩测试领域，文献[9-13]则更多的是从测试的角度分析了减小转矩脉动测试误差的方法。

可见，虽然国内外学者们对磁通反向永磁电机的研究较多，但是在电机优化设计尤其是对齿槽转矩的抑制方面研究往往缺乏理论指导。因此，本文基于解析的方法，推导了齿槽转矩的解析模型，进而从电机设计的角度提出了一种基于转子分段的齿槽转矩抑制方法，文章的技术路线概括如下：

首先，建立了磁通反向永磁电机齿槽转矩的解析模型，推导了转子分段的关键尺寸；然后运用有限元仿真，以一台12槽10极电机为例，验证了所推导的公式正确性；同时，也制作了相应的实验测试用样机，并进行了齿槽转矩的测试；最后得到了一些有用的结论。

1 电机模型

磁通反向永磁电机的结构如图1所示，可以看到，与常见的表贴式永磁电机类似，该电机的永磁体也位于气隙中，只不过它是安装在定子侧（定子齿表面），而非转子侧。本文以一台12槽10极结构的磁通反向永磁电机为研究对象，电机的关键尺寸参数详见表1。

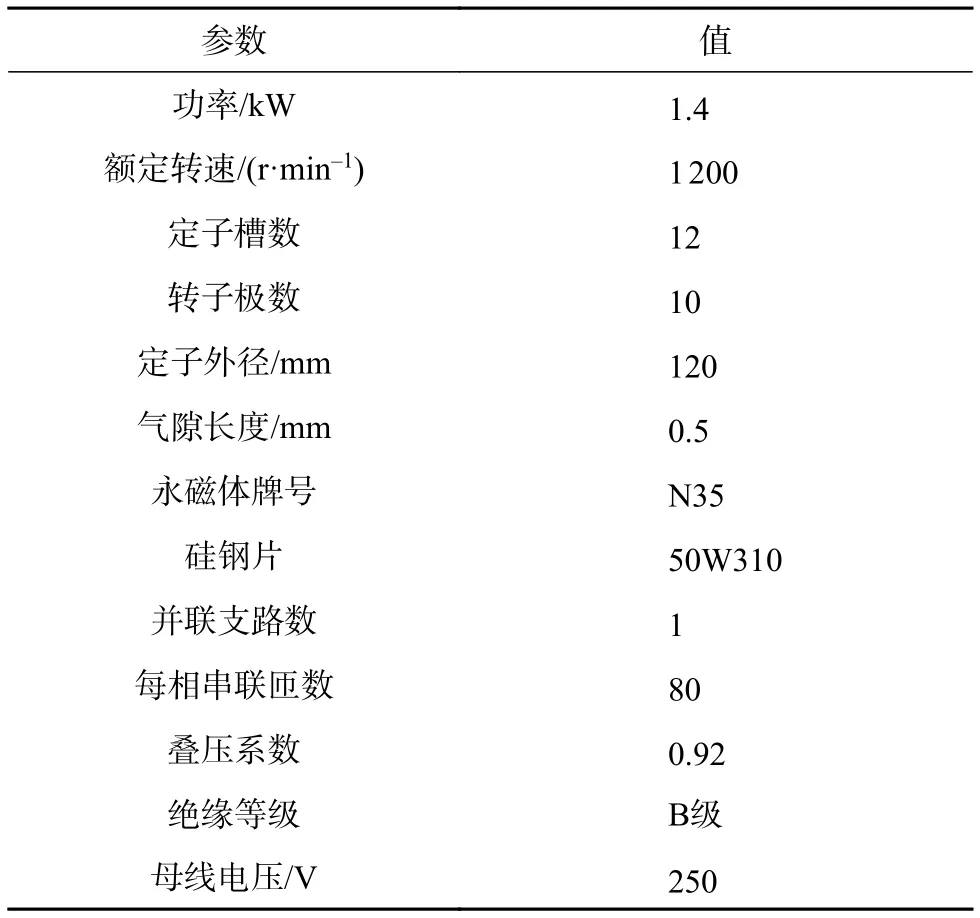
表1 电机关键尺寸参数

图1 常规磁通反向永磁电机3D模型

本文所提出的改进新结构如图2所示，可以看到，转子分为两段结构，每一段的齿宽不同，本文通过合理选取这两个齿宽的组合以达到齿槽转矩优化的目的，进而抑制电机的转矩脉动。

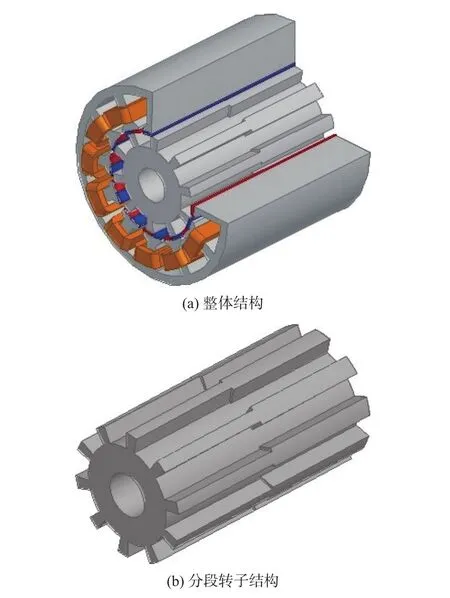
图2 采用转子分段的磁通反向永磁电机

2 齿槽转矩

一般而言，永磁电机的电磁转矩可以由虚功法求解得到[7]：

因此，由式（2）可以判断，从电机本体的角度而言，引起转矩脉动的主要原因包括反电动势谐波、磁阻转矩以及齿槽转矩。一般而言，在磁通反向永磁电机中，由于其空载反电动势波形较为正弦，且电感波形几乎不随转子位置变化而变化，如图3（a）和3（b）所示，因此，该电机转矩脉动产生的主要原因是齿槽转矩，而由磁阻转矩和反电动势谐波引起的转矩脉动可以忽略。因此，本文主要研究如何减小该电机齿槽转矩，进而降低转矩脉动。

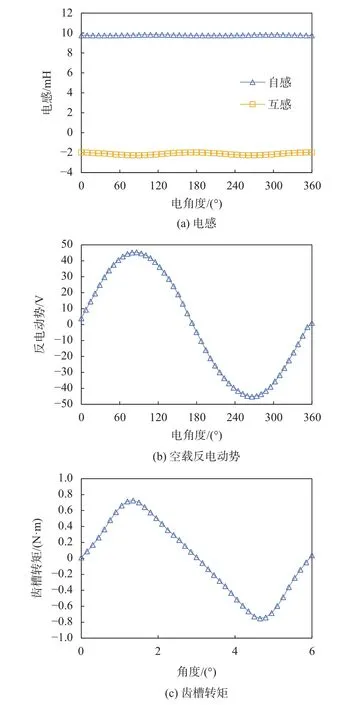
图3 12槽10极磁通反向电机电感、反电动势和齿槽转矩

图3（c）是运用有限元计算得到的一台12槽10极磁通反向永磁电机的齿槽转矩波形，其峰峰值达到了将近1.5 N·m。

3 有限元验证

本节内容以12槽10极磁通反向电机为例，运用有限元模拟仿真，验证第2小节中所推导的公式正确性。

根据式（8），求得该分段12槽10极磁通反向电机每一段的转子齿宽和分别为：

为了验证上述分析，图4（a）为运用有限元仿真得到的齿槽转矩峰峰值与每一段转子齿宽组合的变化关系图。可见，过大或者过小的转子齿宽组合（图中4个角的位置）都会导致较大的齿槽转矩。而当齿宽组合取在图的中心位置时，同样会导致较大的齿槽转矩。而对于式（9）所得到的9°和15°组合附近，齿槽转矩确实较小，这也验证了所推导的解析公式正确性。

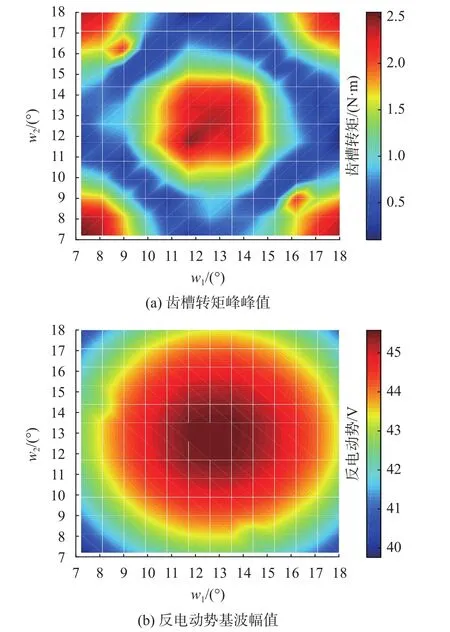
图4 齿槽转矩、反电动势随分段转子齿宽组合的变化关系

图4（b）为运用有限元仿真得到的空载反电动势基波幅值与每一段转子齿宽组合的变化关系图。由图可以看到，反电动势幅值随转子齿宽组合呈现向四周辐射状变化，即越靠近图中中心位置处反电动势幅值越大，而过大或者过小的转子齿宽组合（图中4个角的位置）都会大大降低反电动势的基波幅值。

进一步地，图5运用有限元软件，计算并对比得到了电机优化前后齿槽转矩变化情况。其中，优化结构即图2所示的采用分段转子的结构，而未优化结构即图1所示的常规结构。显然，从图5中可以看到，优化后的电机结构齿槽转矩基波被大大抑制，但是仍然存在少量2次谐波，若要进一步减小齿槽转矩，需要对该2次谐波进行抑制。

相应地，图6对比了电机优化前后额定电磁转矩的变化，可以看到，优化完的电机结构转矩波形比较平滑，转矩脉动由18.3%降低到了3.7%，而平均转矩只减少了5%。

图5 电机优化前后齿槽转矩对比

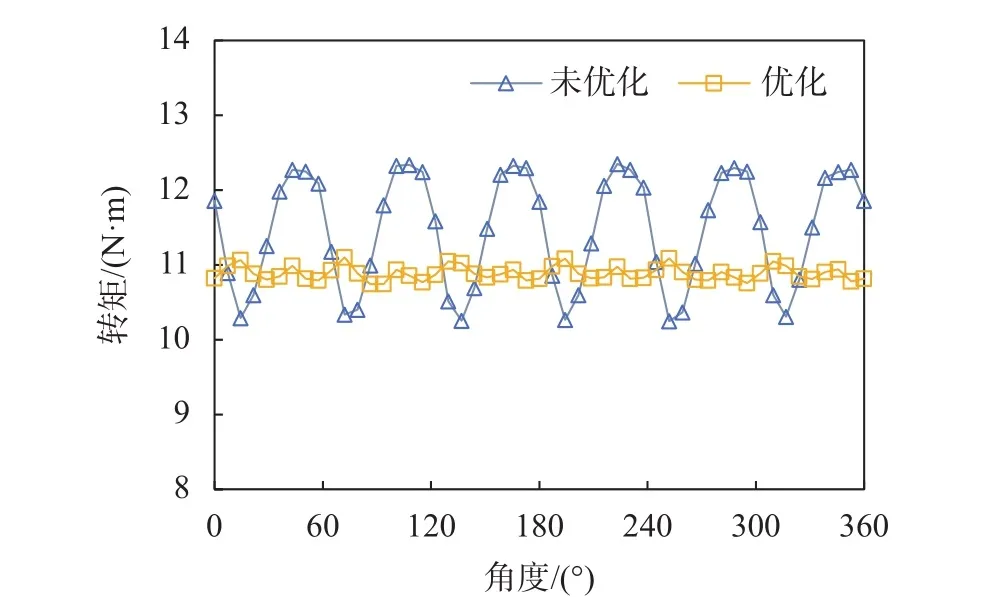
图6 电机优化前后额定转矩对比

如图5（c）进一步研究其他尺寸时的齿槽转矩情况。这里需要说明的是，在这里将一段转子宽度固定在9°，而另一段宽度由5°增加到18°。可见，确实当转子齿宽取15°和9°这个组合时，齿槽转矩达到最小值。

由图5（b）也可以分析得到虽然采用图2所示的分段结构之后，齿槽转矩的基波被大大抑制，而二次谐波仍然存在。因此，为进一步降低齿槽转矩，有必要对其进行抑制。本节内容采用转子分段斜极的方法，如图7所示，斜极的角度如下：

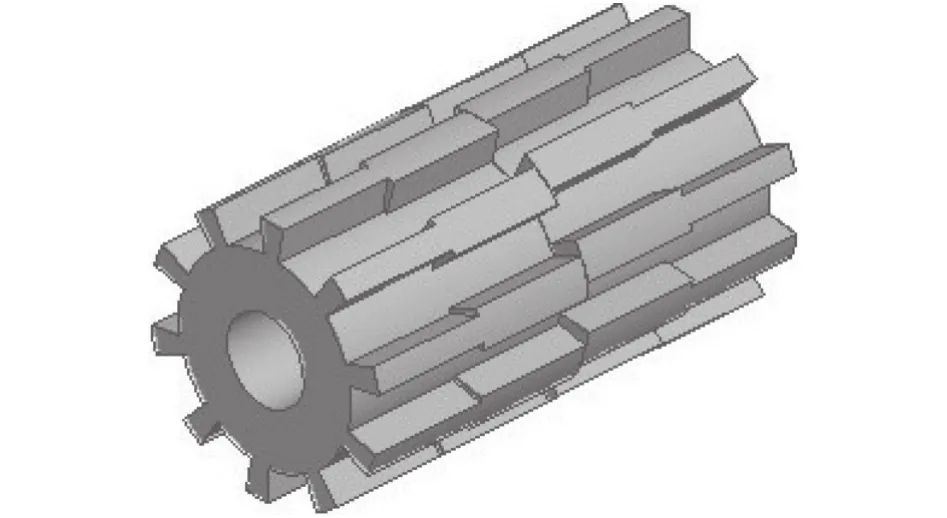
图7 分段斜极

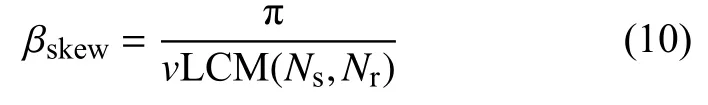
v——齿槽转矩谐波。

因此，针对12槽10极磁通切换电机，通过前面式（10）可以计算得到，理论上的 βskew值为1.5度。为了验证上述分析，图8为通过有限元计算得到的齿槽转矩波形对比。可以看到，当进一步对转子采用分段错极后，齿槽转矩的抑制效果确实最好。这与以上理论分析相符合。当仅对转子采用一次分段时，齿槽转矩峰峰值由1.5 N·m减小到了0.4 N·m，而当进一步对转子采用第二次分段错极后，齿槽转矩的抑制效果确实最好，齿槽转矩峰峰值从1.5 N·m减小到了0.2 N·m，降低了86.67%。

图8 分段错极对齿槽转矩影响

4 测 试

实验是检验理论分析最直接有效的办法[14-16]。为验证本文所提出方法的有效性，试制了相应的实验测试用样机，如图9（a）所示。

4.1 测试平台

齿槽转矩的测试原理如图9（a）所示，整个测试平台最为关键的是其中的转矩传感器，由于齿槽转矩峰值往往较小，因此传感器的精度大小将直接决定测试结果的准确性。测试过程中，需将实验电机固定在平台上，并且与齿槽转矩测试设备保持同心。测试平台的关键参数概括如表2所示。

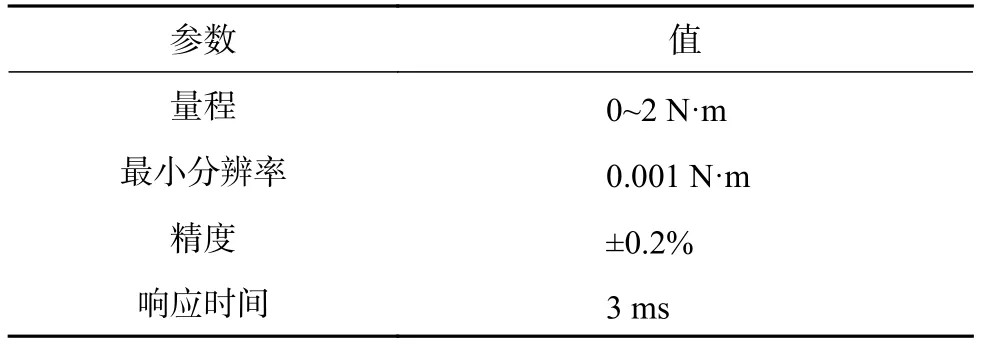
表2 测试平台参数

此外，这里需要强调的是本次实验应在保持实验条件完全相同的情况下重复多次进行以最大程度地保证测试精度。为了减小测试误差，在实验过程中原动机拖动被试样机以0.5 r/min、1 r/min、2 r/min的低转速进行旋转，这样有利于降低因传感器延迟而产生的误差，且每一个转速下同时测量正转和反转两组数据，并且进行多次重复实验。

4.2 测试结果

通过上述实验平台，相应的齿槽转矩测试结果如图9（b）所示，同时，有限元计算结果也在图中进行了对比。可以看到，两者的波形较为吻合，这也验证了本文所提出方案的可行性，样机的关键参数如表3所示。

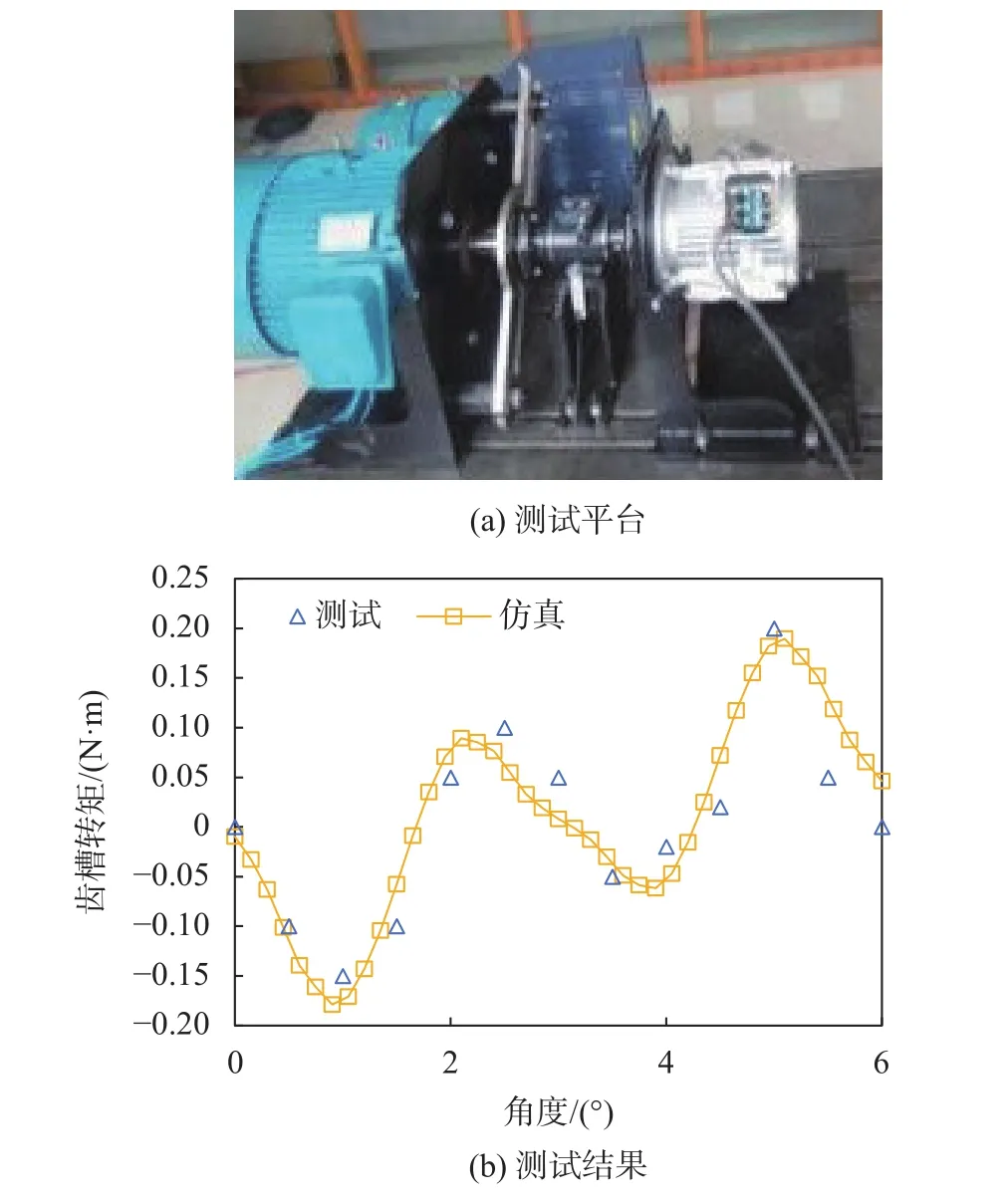
图9 实验测试用样机及其测试结果

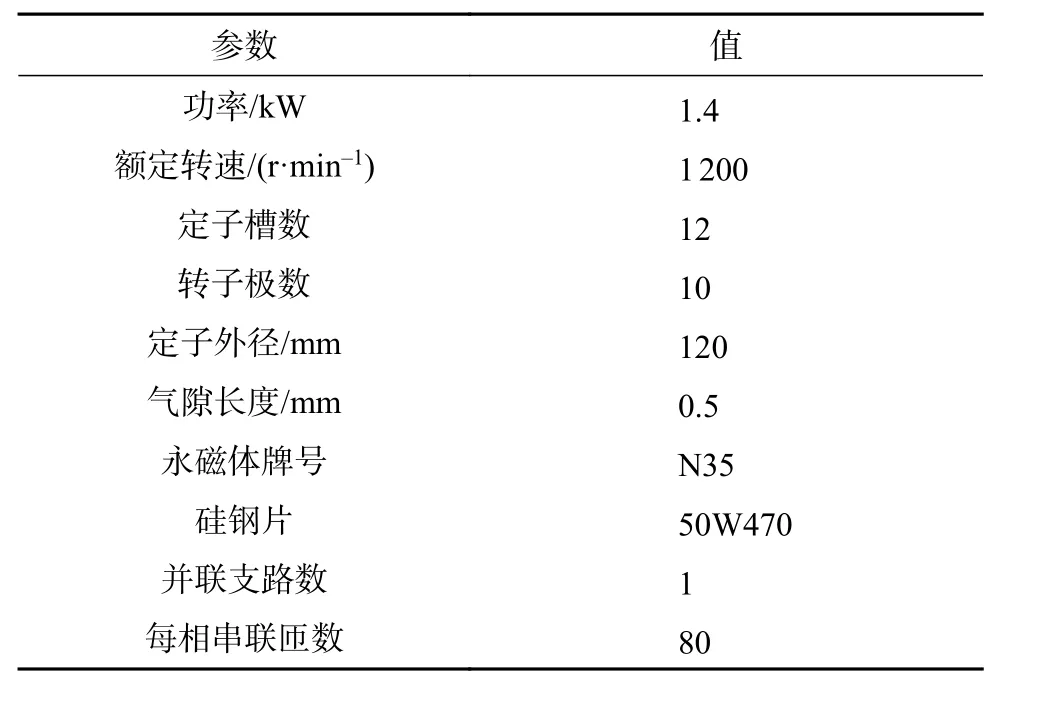
表3 样机参数

5 结束语

本文基于转子分段的方法，提出了一种用于磁通反向永磁电机齿槽转矩抑制的新结构。在该结构中，每一个分段转子的齿宽不同，通过优化齿宽的组合以达到削弱齿槽转矩的目的。建立了磁通反向永磁电机齿槽转矩的解析模型，并且推导了转子分段的关键尺寸。以一台12槽10极电机为例，进行了有限元仿真验证，经研究发现，采用本文所提出的方法，电机的转矩脉动由18.3%降低到了3.7%，而平均转矩只减少了5%。此外，也得到如下结论：

1）当转子采用一次分段错极时可以显著降低齿槽转矩的基波幅值，但是其二次谐波分量依然存在；

2）转子采用两次分段错极后，二次谐波也被大大抑制。