机场飞行保障力量编配辅助决策方法

■刘君阳

引言

空军航空兵作为空中作战力量的主体，肩负着极其重要的战略任务使命。航空兵飞行保障能力和效率的高低能够左右空天战场的胜负，关乎航空兵作战的最终效能。而飞行保障信息化建设的最终目的是为飞行保障力量提高保障效率，保证全面、实时、不间断地满足航空兵部队在进行训练、作战过程中对后勤的需求。飞行保障辅助决策正是为了完成和解决这个问题而提出的。其主要任务是协助生成飞行保障方案，帮助飞行保障指挥员定下保障决心，使飞行保障准备阶段工作更加顺畅。

1 飞行保障辅助决策概念

飞行保障辅助决策以数据挖掘理念为基础，利用传感采集、无线物联、定位技术及相关格式处理与数据存储技术，对保障人员信息、保障装备信息和保障物资信息等相关信息进行收集、处理与分析，基于上级下达的飞行计划和场站的物资装备保障能力，通过科学的计算和优化，最终形成与预定要求相符、与客观情况相容、运行切实可靠的保障计划。

2 飞行保障辅助决策模型构建

2.1 提取保障力量分布状态

构建飞行保障辅助决策模型的关键是提取历史保障活动的力量分布状态，即在明确任务下，外场某一随机流程段的整体保障力量情况。

定义某一流程α 的力量强度

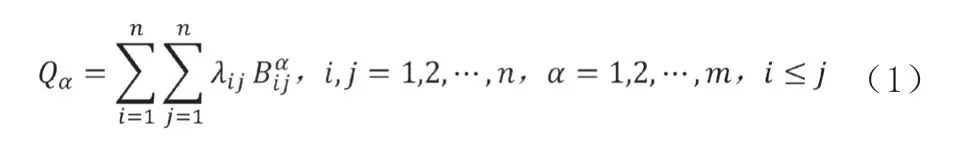
式中：λij表示阶段i，j之间的分布的保障力量需求强度；为各专业保障力量在流程段α 内工作时长的比例，由历史保障活动统计采集数据通过多次迭代取其平均值得到；n为阶段数目；m为流程数量。

为描述某一保障阶段的强度，定义平均保障需求表示为：

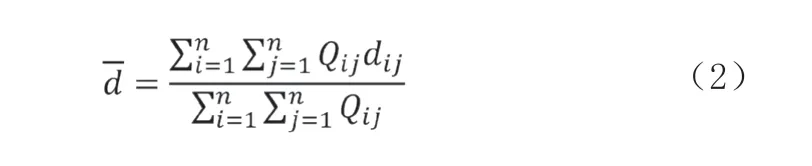
式中：Qij为某一流程下阶段i，j的力量强度；dij为i到j的历史最少需求量。

利用单位矩阵推算方法，进行采用车流平衡约束思想[1]反推保障力量需求强度λij，引入单位矩阵行、列约束系数，对构建的模型进行双重约束，该约束系数的一般计算表达式为：

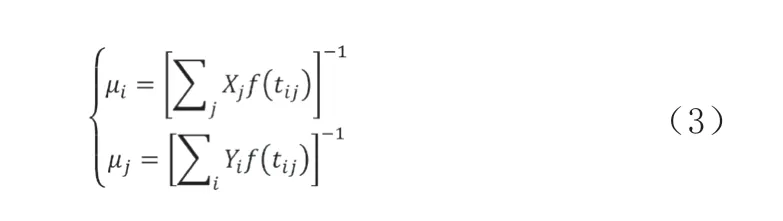
式中：μi、μj分别表示单位矩阵的行、列约束系数；Xj为阶段j的力量需求量；Yi为阶段的i力量空闲量；f(tij)为阻抗函数。

根据式(3)得到阶段i，j之间的能够传递的保障力量

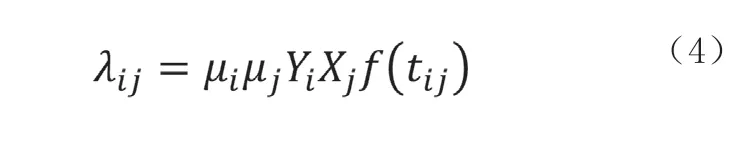
将式(4)带入(1)得到某一时间段的保障力量。

按照上述过程，通过分析飞行保障过程中的人装物力量活动状态，即可得到某一随机流程段的保障力量计算结果。

2.2 基于贝叶斯网络量化保障活动

首先根据贝叶斯网络特点，进行变分贝叶斯推断。利用最小化奇异距离准则[2]，优化虚拟分布函数u(θt)以及后验概率密度函数v(θt|pt)，定义2 个函数对称中心之间的距离

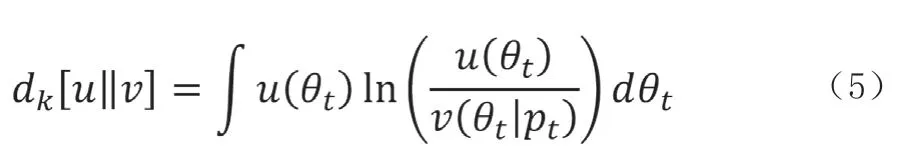
式中：θt为全局变量，pt为观测向量后验概率。假设全局变量θt对应的虚拟分布函数可分解为：

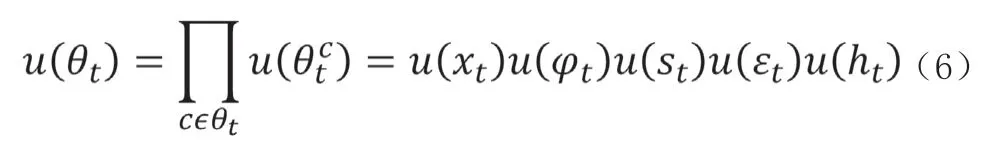
根据式(6)结果，利用贝叶斯网络分析保障活动的进程转移量，预测下一时段需要选择的保障活动。由似然分布的基本定义可知：非线性结果与精度存在不确定性，此时的后验分布v(θt|pt)会失去闭合表达能力。因此根据贝叶斯网络的多层动态特征，对后验分布v(θt|pt)进行调整，得到单变量的最佳变分近似值

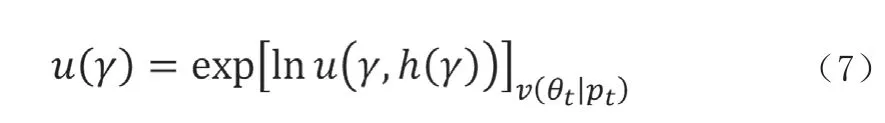
式中：γ 为先验参数，h(γ)为贝叶斯网络中的马尔可夫毯[3]。

根据式(7)，对保障活动中的保障进程状态量化跟踪，近似掌握保障人员的实时进程，再通过贝叶斯网络进行数据融合，为决策模型提出基础规划决策数据。

2.3 构建满足平衡力量编成的辅助决策模型

2.3.1模型目标函数及约束条件

假设飞行保障力量编成平衡规划指标为K，则该指标的计算表达式为：

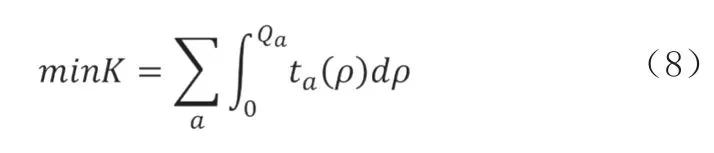
式中：ta(ρ)表示保障强度密度为ρ 时的某一个保障力量活动时间。其表达意义为：对确定流程的保障任务，运用更少的力量就能够在规定时间完成相同保障任务，相对应的支援和应急力量就能更加充裕，对整体来说就是对保障效能得到了更高的释放。

保障强度密度ρ 定义为单位时间内处于工作状态的保障力量强度，即。

其中ℇ ∈(0 ∪1)，属于判断系数，主要取决于l阶段任务需求。

飞行保障力量编成平衡规划限制条件为：

当式(9)基本条件成立时，式(8)计算成立。

2.3.2平衡力量编成等价性评估

对于流程D，式(8)关于式(9)的拉格朗日方程为：

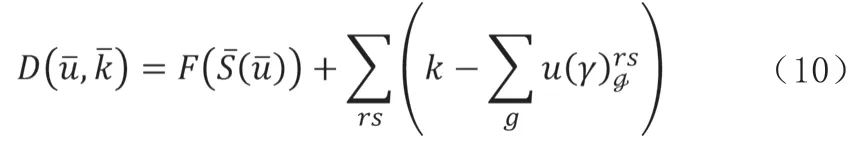
式中：D(u,k)为拉格朗日函数，F(S(u))为力量编成阻抗函数，k为留守恒约束的拉格朗日乘子。

辅助决策模型需要满足某一流程保障时间函数的假设，即

式中t(q)为某一流程中保障活动时间参数。

3 仿真及验证

3.1 验证评估标准制定

定义保障力量出动率体现保障活动强度：

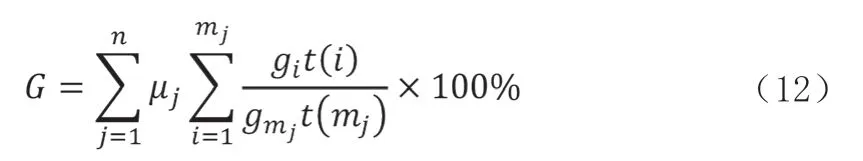
其中μj为第j个部门的保障活动系数，n为保障单位总数，mj为第j个单位保障人装物总数；gi为每个单位每项人装物出动调拨数量，t(i)为对应人装物参与保障活动的时间函数；gmj为gi对应人装物编制上限，t(mj)为该单位保障活动的时间函数。

定义保障满足率体现决策优化程度：

式中：按照既定流程安排条件，NTk为每项保障活动预先需求时间，STk为仿真环境下保障活动运行时间分布取期望值，n为保障活动总项目数。

3.2 仿真结果

3.2.1流程仿真输出决策依据

设定保障业务为机务检查与维护、燃油与特种油料加注、充气、充电及弹药挂载，设定保障人员编制、装备编制、物资存储量可变可控，规定保障活动时间与资源消耗服从相关分布[6]，使用Anylogic 软件对保障流程仿真，输出模型所需路程、时间、空间信息。

3.2.2理想约束条件下决策结果

基于已完成的活动数据进行决策仿真；此时力量出动率G=82%，保障满足率Q=102%，活动总时长T=80min。得到飞行保障活动流程甘特图如图1 所示：

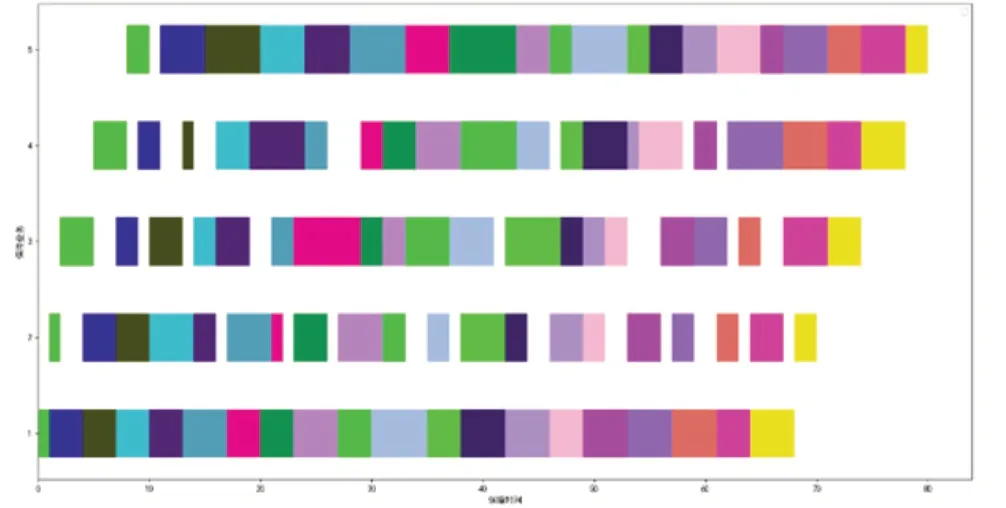
图1 理想约束决策下运行仿真结果

3.2.3过负荷条件下决策结果

在保证保障活动流程与资源消耗服从相关分布不变的情况下，改变人装编制、物资库存数据，使部分保障力量小于理想决策方案数量，此时强调战时非理想条件的决策活动；此时力量出动率G=97%，保障满足率Q=74%，活动总时长T=100min。得到飞行保障活动流程甘特图如图2 所示：

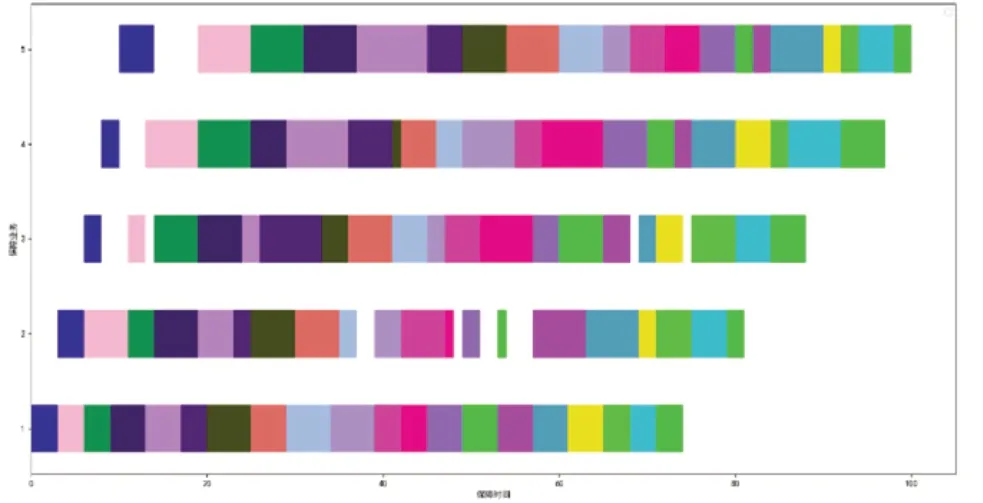
图2 过负荷决策下流程运行仿真结果

由以上结果可以看出，该辅助决策模型通过与流程规划配合工作，可以根据不同保障流程与力量编制制定不同保障计划方案，其对活动要素的决策由飞行保障力量编成平衡规划指标为K决定，决策能力通过流程仿真得到的力量出动率及保障满足率共同体现，最终目的是保证更低力量出动率条件下实现更高保障满足率和更快的保障活动时长，能够达成科学决策辅助的功能。

4 结论

本文提出了一种基于贝叶斯网络的飞行保障辅助决策模型，通过计划流程——制定决策——优化流程——优化决策——计划流程的闭环实现，一定程度上填补了飞行保障辅助决策问题领域由理论上升至实践的空白。结果表明对飞行保障的辅助决策需要明确流程任务和力量编成情况，在此基础上采用基于贝叶斯网络的飞行保障辅助决策模型，能够较为科学地实现保障力量编配组织，对该领域相关问题的研究有一定借鉴意义。