Hilbert空间中关于有限时滞随机发展方程的Trotter-Kato逼近体系*
2022-12-13戴凌飞
刘 明,戴凌飞,张 霞
(天津工业大学数学科学学院,天津 300387)
0 引 言
近年来,随机发展方程的逼近理论研究已引起了国内外许多相关领域著名学者的关注,如:Ichika‐wa[1]研究了半线性随机发展方程的Yosida逼近体系,并给出了该体系下适定解的指数稳定性,在此基础上,Govindan 和 Ahmed[2]进一步证明了此类方程适定解的鲁棒稳定性;Ahmed和 Ding[3]研究了半线性随机发展方程中的非线性漂移项同时依赖于解过程在给定时刻的状态和概率分布,且常数可加扩散项为正对称有界算子时适定解的性质,并建立了方程关于适定解的Yosida逼近体系,从而给出解的指数稳定性;Govindan 和 Ahmed[4]研究了当方程中的非线性漂移项如文献[3]中定义,但常数可加扩散项为算子值函数时的情况,接着通过方程适定解建立了 Yosida逼近体系;Govindan[5-7]研究了上述3类随机发展方程适定解的Trotter-Kato逼近体系,并给出了其在该逼近体系下适定解诱导概率测度的弱收敛性,以及关于方程参数依赖性的经典极限定理.而且Trotter-Kato逼近理论研究在自然科学、工程学以及金融数学等众多学科所诱导的随机动力系统的模拟计算中起着越来越重要的作用.本文拟介绍随机发展方程的Trotter-Kato逼近理论的研究进展,并将在此基础上研究有限时滞随机发展方程关于适定解的Trotter-Kato逼近体系.
首先,回顾半线性随机发展方程
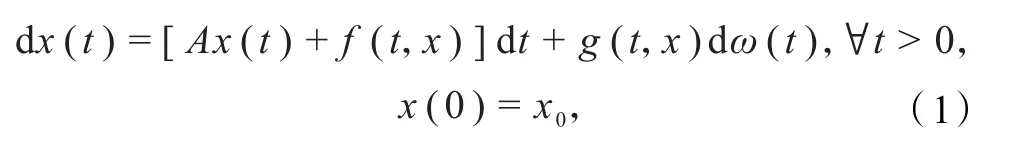
式中:A是Hilbert空间X上有界线性算子强连续半群{S(t), t≥ 0}的无穷小生成元;f是定义在 R+×X上的X值函数;g是定义在R+×X上的L(Y,X)值函数;ω(t)是Y值维纳过程;初值x0是F0可测X值随机变量 .1982年,Ichikawa[1]证明了方程(1)适定解的存在唯一性;2015年,Govindan[6]通过适定解将Trotter-Kato逼近体系引入到该方程并得到了一些重要的结论;2015 年,Govindan 和 Ahmed[4]对方程(1)中的非线性漂移项f进行了推广,使其同时依赖于随机过程x(t)在t时刻的状态和概率分布μ(t),改进后的方程为

1995 年,Ahmed 和 Ding[3]考虑了当常数可加扩散项的情形.此时上述方程变为:

式中Q是X上的正对称有界算子.2006年,Govin‐dan[5]研究了方程(3)上的 Trotter-Kato 逼近体系 .2018 年,Govindan[7]根据方程的适定解引入了 Trot‐ter-Kato逼近体系,并给出在该体系下适定解诱导概率测度的弱收敛性.
基于此,本文将致力于研究有限时滞随机发展方程的Trotter-Kato逼近体系,进而得到一些有意义的结果.方程的具体形式为
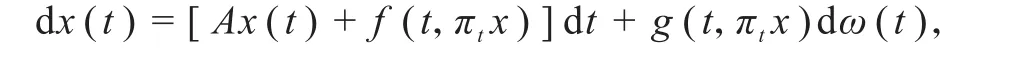

1 预备知识


2 Trotter-Kato逼近体系
随机发展方程(4)适定解的存在唯一性可由命题2.1得到,本文在主要结论定理2.1中证明了当p≥2时Trotter-Kato逼近体系下的适定解收敛于方程(4)的适定解;在此基础上,定理2.2给出关于零阶逼近的结论用以估计逼近的误差.

2.1 适定解的收敛性
现考虑如下随机发展方程



2.2 零阶逼近

为得到关于零阶逼近的结果,先给出如下假设:



3 经典极限定理



4 应 用


这证明了 f:R+× X → X.类似地,也可证明 g:R+×X → L(Y,X).因此方程(19)中的 A、f和 g均符合方程(4)中所给出的定义,即方程(19)可以看作是方程(4)的抽象形式.
这表明在一定的假设条件下,本文前面所给出的在Trotter-Kato逼近体系下适定解的收敛性,零阶逼近以及经典极限定理等结论对方程(19)都是同样成立.
