RFID标签冲突分离的最大后验概率聚类
2022-12-13郭佳雯吴海锋桂妮霞吴晓刚陈跃斌
郭佳雯,吴海锋,2,桂妮霞,吴晓刚,曾 玉,2,陈跃斌
(1.云南民族大学电气信息工程学院,昆明 650500;2.云南省高校智能传感网络及信息系统科技创新团队,昆明 650500)
引 言
无线射频识别(Radio frequency identification,RFID)技术兴起于20世纪80年代,目前已成为“物物互通”的物联网核心技术之一。由于RFID采用无线射频通信,数据交换无需物体间接触和人工参与,因此在物联网信息采集层发挥了重要作用。
物联网中,当RFID阅读器同时识别多个附有标签的物品时,各标签信号在共享信道中难免发生冲突。标签冲突一般在介质接入控制(Media access control,MAC)层[1⁃4]中解决,其基本原理为:标签和阅读器随机通信,若发生冲突则再随机选择时间重发,直到发送成功。然而,该方式在标签过多时,重发次数增多,通信效率不高。冲突信号实质为各标签信号的叠加,对冲突信号分离后可被成功解码。此时,冲突信号不会被视作无效信号,因此可降低重发次数,从而提高通信效率。
在传统的分离方法中,无监督聚类[5⁃8]是一种常用方法,由聚类结果对冲突信号进行判决即可完成分离,其主要步骤则是确定聚类中心[9]。K均值[10]是应用较为广泛的无监督聚类算法,该算法通过不断迭代获得聚类中心。为获得准确的聚类中心,K均值通常需较多的迭代次数,当样本数量较大时,该算法的运行时间较长,且其还需预知聚类数才能有较好的聚类效果。为减少运算时间,可采用一维投影图法[11]进行聚类,将原二维平面聚类投影至实轴或虚轴上,计算冲突信号采样点落在实轴或虚轴区间上的点数,通过寻找点数的局部最大值确定聚类中心坐标。相比K均值,一维投影图法可显著降低算法复杂度,但由于信号簇分布随机,因此该方法的稳定性不高。例如,当多个信号簇中心的某一轴的坐标比较接近时,该轴方向上多个局部最大值会退化为单个值。
本文提出一种蒙特卡罗最大后验概率(Monte Carlo⁃maximum posteriori probability,MC_MAP)聚类方法来完成冲突信号分离。首先,将冲突信号的采样点映射至一个具有若干网格的二维平面中。然后,计算落在各网格中采样点数。最后,利用窗口法计算点数的局部最大值,该值对应的网格坐标即是聚类中心点。与上述两种传统算法不同,本文算法无需预知聚类数和不断迭代,算法复杂度较低。二维平面窗口法可防止一维投影法局部最大值退化引起的算法稳定性不高的问题,继而实现较准确的信号分离。实验中,分别采用仿真和软件无线电的FM 0码[12]信号来测试本文方法的分离性能,并对分离后信号用匹配滤波器和相位跳变[13]进行解码。实验结果表明,本文算法的误码率、分离效率能达到与K均值近似的性能,但运行时间可大幅减少。另外,在某些特定的信号衰减系数下,本文算法聚类准确度优于一维投影图算法,可达到较好的分离效果。
1 研究背景
当多个RFID标签发送信号,对于同一阅读器,将接收到多个标签信号的叠加。通常,标签信号为单极性码,则经同相正交(Inphase quadrature,IQ)解调后,其采样点映射到复平面上会出现M=2N个簇[14],即聚类的类别数,其中N为冲突标签数。图1(a)给出了两个标签的冲突信号,图1(b)为冲突信号映射至复平面。由该簇中心点构成的集合可表示为H={0,h1,h2,h1+h2}[11],其中h1、h2分别为两个标签的衰减复系数。经聚类后,任何一个采样点均可根据式(1)中的中心点分离成两个标签信号采样点构成的矢量,分离结果构成的集合表示为D={[0,0],[1,0],[0,1],[1,1]},其中D和H的每一元素构成[15]一一映射关系,表示为

图1 两个标签冲突信号示意图Fig.1 Schematic diagrams of conflict signal be⁃tween two tags

式中:d m(m=1,2,…,4∈H)分别为元素[0,0],[1,0],[0,1]和[1,1];δm(m=1,2,…,4∈H)分别为0,h1,h2和h1+h2。
上述分离过程中,核心步骤是聚类,即寻找各簇中心点。由于信道衰减系数h1和h2未知,因此上述聚类是无监督聚类,可采用K均值实现。K均值首先需要预知聚类数,选取与聚类数相等的一些随机点作为初始聚类中心[16]后,计算每个数据点与初始聚类中心的距离,再将这些数据归类至与其距离最近的类,由归类的点重新获得新的聚类中心[16],然后计算新聚类中心下的距离值,重复迭代,使得计算的距离值逐渐减小直至收敛,则算法结束。近年来,对初始中心的选择和预先确定确切聚类数有一些相关研究实验结果表明所提方法的有效性[17],并对迭代次数作出改进,其实验结果表明在不降低聚类效果的前提下[18],迭代次数有所降低。为进一步减少复杂度,在RFID冲突信号的分离中,目前,还可采用一维投影图法[11]来寻找聚类中心坐标,不仅聚类效果更好,且计算复杂度更低[19⁃20]。将冲突信号映射至二维复平面后,在实轴和虚轴上划分若干等距离区间,计算冲突信号采样点在实或虚轴上的投影落在各区间的点数,各点数的局部最大值所对应区间位置即是中心点坐标,如图2所示。

图2 一维实轴和虚轴方向投影示意图Fig.2 One⁃dimensional projections on real axis and imaginary axis
2 问题提出
在K均值算法中,调整一次聚类中心需迭代一次,准确的聚类中心与迭代次数相关,较多的迭代次数可保证较准确的中心点,但计算复杂度会随之增加,该计算复杂度O可表示为

式中:s为数据样本的数目为调整数据样本与聚类中心距离的复杂度;x a、x c分别为数据样本点和聚类中心点的位置,其与维度有关,例如,当投影到一维平面时,其为标量,l为迭代的次数。另外,较多的数据样本点数也会增加迭代次数,延长计算时间。在RFID冲突分离中,若采用复杂度较高的聚类算法会增加分离时间,从而降低了阅读器与标签的通信效率。
一维投影法在一维坐标轴上寻找峰值,其优点是无需迭代,因此计算复杂度可大幅下降。然而,冲突信号的聚类中心分布是随机的,该方法在某些分布情况下并不适用。图3给出了一个例子,圆圈中两个簇的位置在其中一个投影方向上较为接近,因此在该方向的投影上形成了峰值重叠,最终只能得到3个局部最大值。

图3 一维投影法聚类点缺失情况示意图Fig.3 Missing clustering points by one⁃dimensional pro⁃jection method
3 算 法
3.1 系统框图和模型
图4给出RFID冲突信号分离和解码的系统框图。当一个阅读器的电磁场范围内存在多个标签时,阅读器采用随机多址方式与标签通信,如ALOHA方法[21],即标签随机选择时隙与阅读器通信,当一个时隙内有两个或两个以上的标签发射信号则发生冲突。此时,冲突信号是多个标签信号的叠加信号,采用聚类方法对其分离。对该叠加信号进行IQ解调,然后映射至二维复平面,经聚类后得到聚类中心,再由聚类中心进行分离,分离的信号经解码后即可得到标签ID。

图4 系统框图Fig.4 System block diagram
假定在一个时隙内有N个标签发送信号,则阅读器接收的将是这些信号的叠加,经IQ解调后得到的信号y(t)可表示为
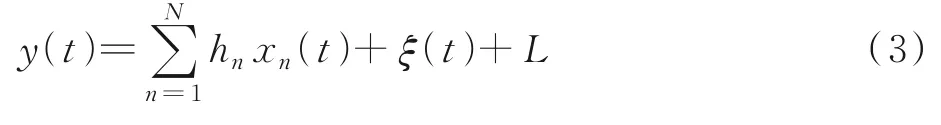
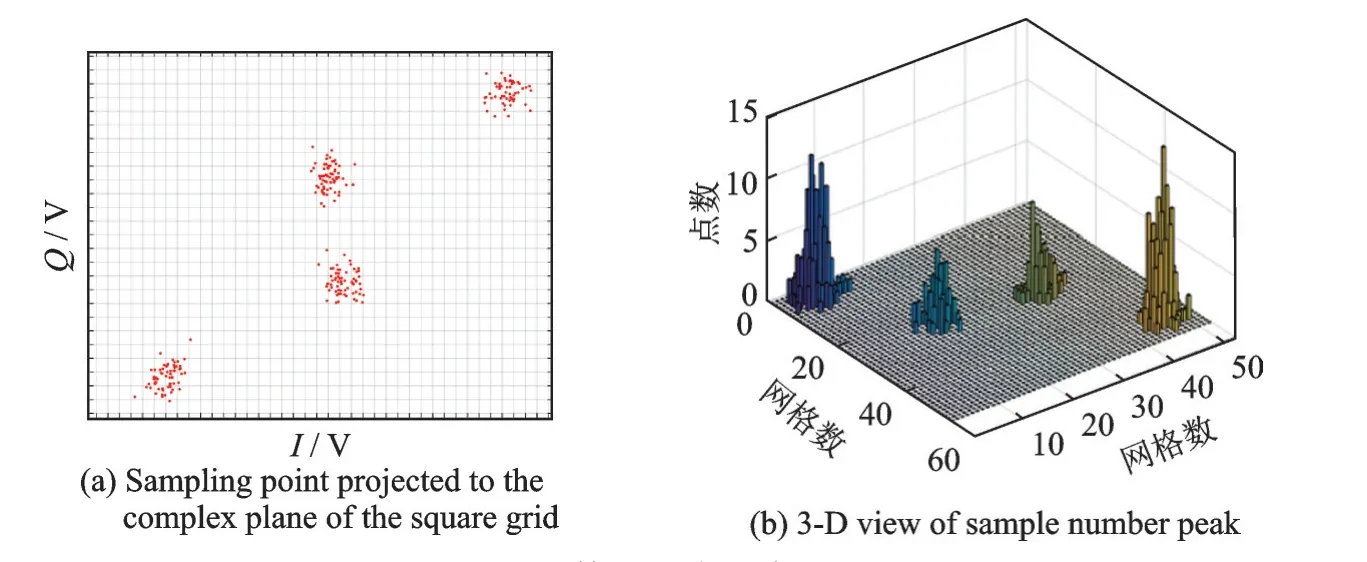
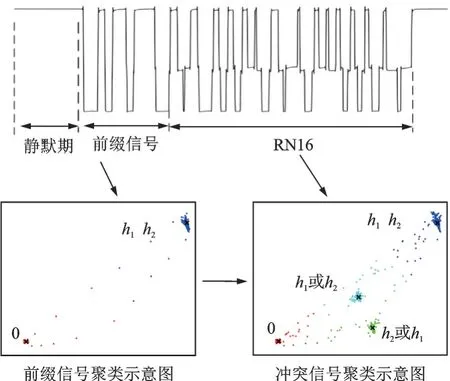
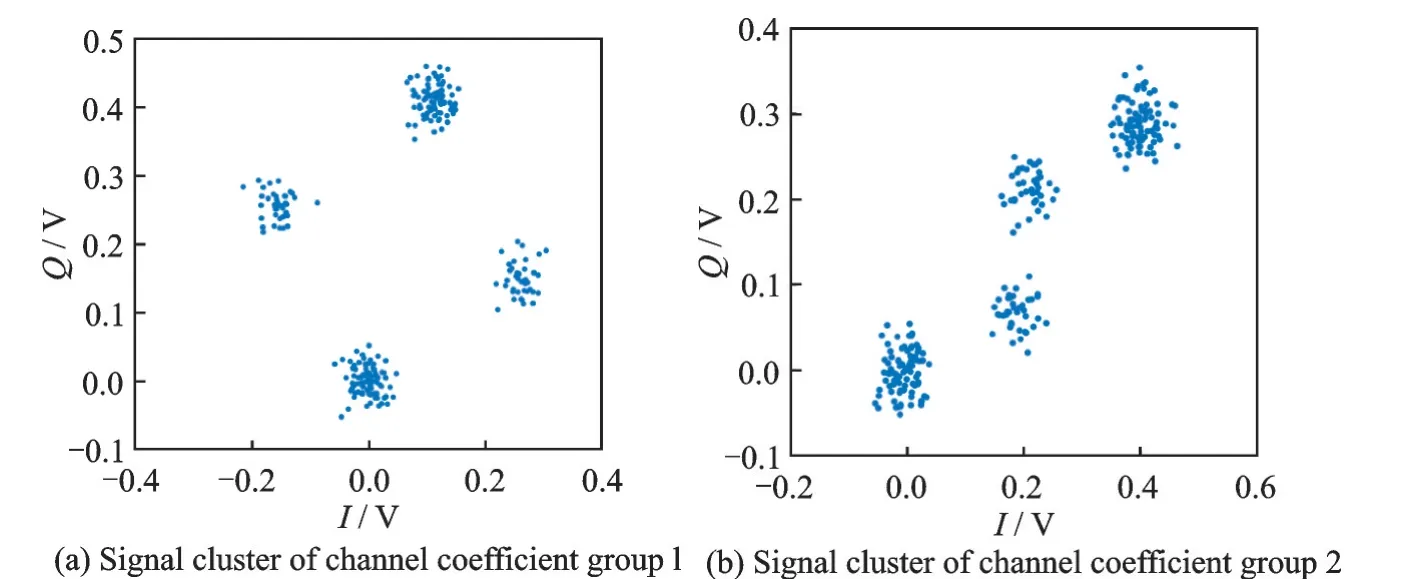
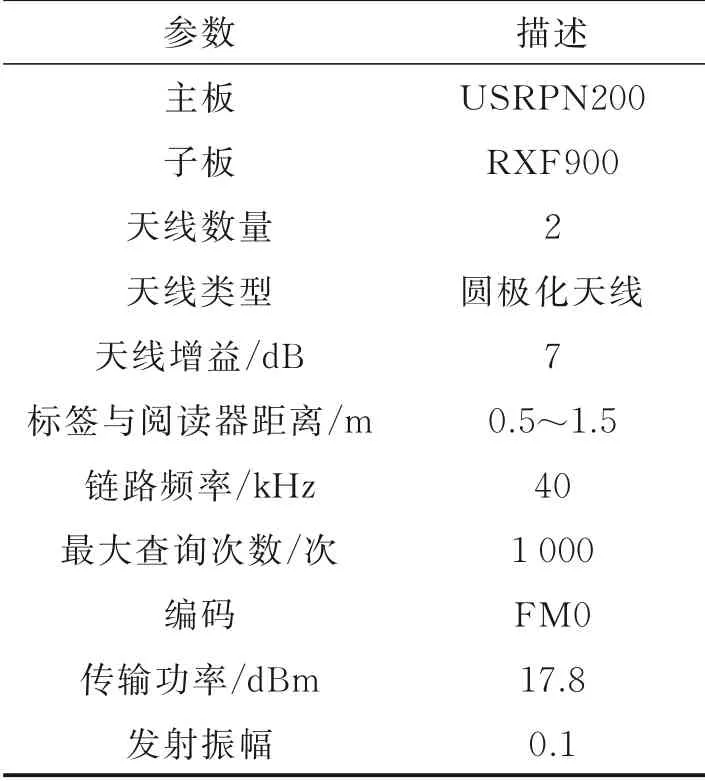
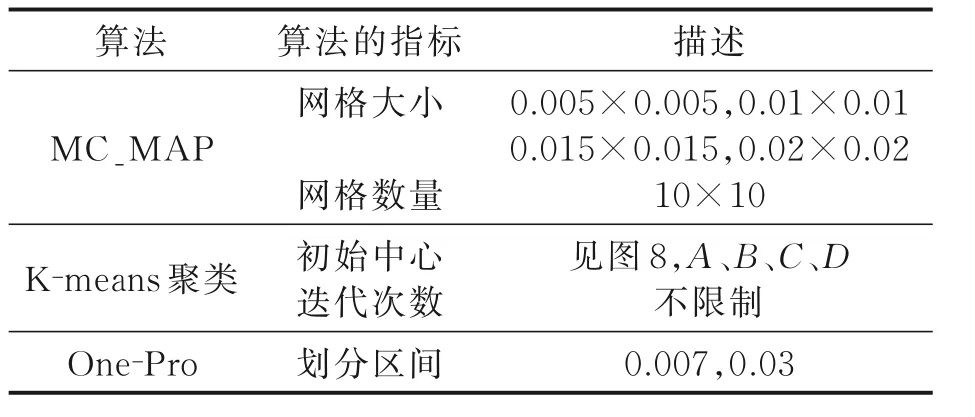
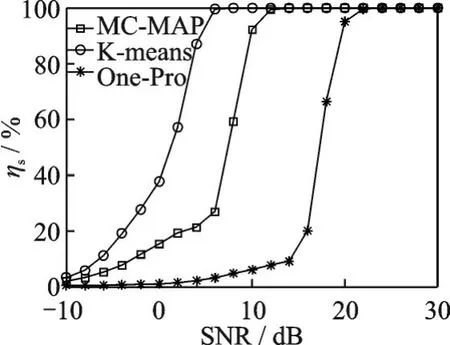
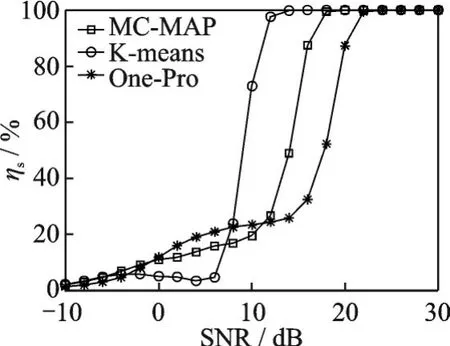
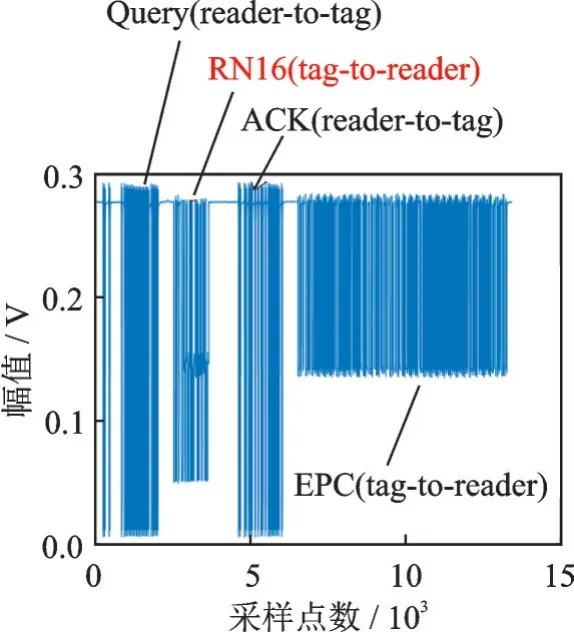
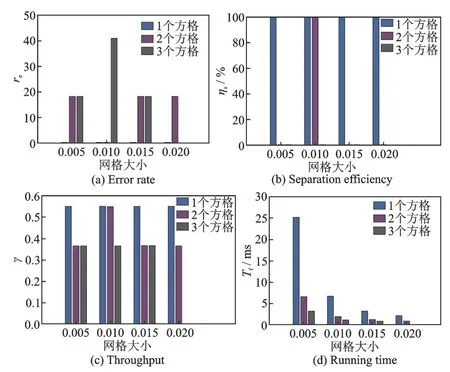
式中:L为载波泄露[22];hn为第n个标签信号的复衰落系数,该衰落系数在很短的一个通信时间内可视为平坦性衰落的线性时不变信道[23];为第n个标签信号;sn,k∈{0,1}为二进制数序列;K为序列长度;g(t)为矩形脉冲波形,当0≤t MC_MAP聚类过程如图5所示,先将解调后的冲突信号采样点映射至一个二维复平面中,该平面被划分为若干个正方形网格,然后统计落在每个网格中的点数,根据统计的点数画出柱状图,各局部峰值就可视为每个簇的聚类中心点。 图5 算法聚类示意图Fig.5 Clustering process 设yi=y(iΔt),i=1,2,…,I为冲突信号y(t)采样后的I个采样点,其中Δt为采样周期,将yi投射至一具有J个正方形网格的复平面上。令p(j|y i∈Cm)为采样点yi属于第m个簇时落在第j个网格的概率,其中Cm表示第m簇点的集合,那么第m个聚类中心点所在网格的位置ĵm可通过最大后验概率估计得到,表示为 该式表明,若属于第m簇的采样点落在第个网格的概率最大,那么该网格就为第m簇中心所在网格。 为求解(4),可采用蒙特卡罗方法[24]。对式(4)中的后验概率有 式中:为第m簇的点落在第j个网格中的数目,|·|为集合势。原后验概率可以用某簇的采样点落在网格内的数目来表示,若I足够大。将式(5)代入式(4)中,最后的蒙特卡罗最大后验概率估计可以表示为 因此,求解式(5)只需在二维平面上找到网格内采样点数的峰值。设cj表示第j个网格的中心,则将峰值对应网格的中心点cĵm近似作为第m簇的聚类中心点。 得到聚类中心点后,应确定中心点对应于式(1)集合H的何元素,以此完成分解。例如,若对应0,则属于该类的采样点y i分解为[0,0];若对应元素h1+h2,则y i分解为[1,1]。将确定两个冲突标签中4个聚类中心,m=1,2,…,4与集合H的各元素的对应关系。 标签在发射信号前会出现一段静默期[25],此时阅读器接收的信号仅含有载波泄露L,因此该时刻的信号幅值应与集合H的0元素的幅值相等。据此,与L最近的聚类中心将对应元素0。另外,在EPC C1 Gen2标准中,每个标签在发射RN16之前均有一段前缀信号[12],由于每个标签的前缀信号均相同,因此对于两个标签的冲突情况,在该段时间内的两个聚类中心将对应元素0和h1+h2。由于对应0元素的聚类中心已经确定,因此剩下的聚类中心将为h1+h2,如图6所示。最后,对于两个冲突标签,剩余的两个聚类中心将分别对应于元素h1和h2,或h2和h1,如图6所示。由于此时的冲突标签只有两个,以上两种对应的情形所得到的分离结果只会导致标签的分离顺序不同,并不改变分离结果,因此任选一种对应关系即可。 图6 确定中心点对应关系图Fig.6 Determination of correspondencediagram of the center point 确定对应关系后,通过计算距离对采样点yi判决以确定其对应何类,表示为 式中为通过判决所估计的类别。然后,由式(1)可对采样点yi进行分离,表示为 信号分离后,本文中采用FM 0编码[26]方式对标签信号进行编码,解码采用匹配滤波器和传统的相位跳变,得到标签ID。算法步骤如下。 输入: 冲突信号数据采样点[yi][i=1,2,…,I] 输出: 聚类分离矢量[d m|yi] 已知条件: 正方形网格[j]的中心坐标[cj][j=1,2,…,J] 步骤: (1)由式(2~5)得到聚类中心点坐标[cjm]; (2)由式(6)判决确定其类[δm]; (3)由式(7)得到分离信号[d m|yi]。 实验中,采用动态帧时隙ALOHA[21]和物理层分离联合解决标签冲突问题,由于动态帧时隙ALOHA中,帧长将近似设置为标签数目,因此平均一个冲突时隙中,冲突标签为2.33[27],大部分冲突时隙内的标签为2~3个。据此,本文算法主要解决一个冲突时隙中存在两个冲突标签的分类情形,此时,聚类簇的数目为4,当冲突标签大于2时将视为无法分离。 RFID系统参数设置参照EPC C1 Gen2标准[12],数据采用模拟数据和实测数据。仿真实验中,冲突信号由式(3)得到,为两个RFID标签的基带信号与高斯白噪声的叠加,主要参数设置如表1所示。不同的信道衰落系数会产生不同的冲突信号簇类图,从而影响聚类结果,因此表2给出了两组衰落系数,其映射至复平面的信号簇如图7所示。信道衰落系数为组1时,信号簇如图7(a),各簇中心在实轴或虚轴上均未有重合现象。信道衰落系数为组2时,信号簇如图7(b),此时有两个簇中心在实轴方向相近。 表1 仿真数据参数设置表Table 1 Simulation data par ameter setting 表2 信道系数衰落设置Table 2 Channel coefficient fading setting 图7 两组信道系数产生的信号簇Fig.7 Signal clusters generated by two sets of channel coefficients 实测数据由USRP软件无线电产生,依据EPC C1 Gen2标准构建超高频RFID系统,软件采用GNU Radio实现,详细参数参见表3,代码下载地址为https://github.com/nkargas/Gen2⁃UHF⁃RFID⁃Reader[28]。 表3 USRP系统设置Table 3 USRP system setting 为评判本文算法性能,实验对蒙特卡罗最大后验概率法、K均值和一维投影图法进行性能对比,3种算法分别用MC_MAP、K⁃means和One⁃Pro来表示。另外,由于划分的网格大小对算法的性能指标有影响,因此实验中对比了4组大小网格结果。以上算法参数设置详见表4。表4中4组网格大小数据为实测数据实验网格大小的参数设置。由于仿真数据样本取值范围受信噪比影响不断变化,因此表里固定了网格的数量。A、B、C、D点为取实部和虚部的最大值和最小值两两组合得到。确定初始中心点后使之不断迭代调整,直至中心点收敛,因此不限制迭代次数。 表4 各算法描述Table 4 Description of each algorithm 实验中,采用如下指标对算法的性能进行对比。误码率re定义为解码有误的码元数Ne与标签总码元数Nt的比值,表示为 式中分离效率ηs定义为成功解码标签个数ns与总标签个数nt之比,表示为 式中只有当标签一次发送的所有码元均被成功解码才视为该次标签被成功解码。吞吐量γ定义为平均一个帧中成功解码[15]的标签数Ls与该帧长Lt的比值,可表示为 实际聚类中心点与期望中心点的误差值ε用来衡量各算法的准确度,计算第m簇中心点第w次的实验结果与第m簇期望中心点cm的误差,可表示为 式中W为算法重复次数。 图8 K均值聚类初始中心点选取图Fig.8 Initial center selection of K⁃means clustering 当信噪比取值为-10~30 d B时,图9~14给出了在不同信道系数下3种算法的误码率曲线图、分离效率曲线图以及吞吐量曲线图来验证各算法的性能。另外,为了说明各算法的准确度和复杂度,还给出了在第1组信道系数下各算法计算得出的聚类中心点坐标与期望中心点坐标的误差和各算法计算中心点所需的平均运行时间。 图9给出了第1组信道系数下各算法的误码率,从图9中可以看出,MC_MAP算法的误码率低于One⁃Pro算法,但高于K⁃means算法。图10为第2组信道系数下各算法的误码率曲线,在信道系数第2组中,实轴方向有两簇信号位置相近,信号簇分布示意图见图7(b),One⁃Pro算法在该情况下实轴方向无法计算出完整的聚类中心点,在虚轴方向得到的实验结果曲线图与第1组时类似,误码率仍高于本文算法。MC_MAP算法与K⁃means算法受到信道系数的影响误码率都有升高,但是MC_MAP算法受信道系数影响程度高于K⁃means算法4 dB,此时MC_MAP算法的抗衰落性能强于K⁃means算法。 图9 第1组信道系数下各算法误码率Fig.9 Bit error rates of the three algorithms under the first group of channel coefficients 图10 第2组信道系数下各算法误码率Fig.10 Bit error rates of the three algorithms under the second group of channel coefficients 图11,12给出了两组信道系数下的分离效率。从图11,12可得,在高信噪比时3种算法的分离效率都能达到100%。图12中,受到信道系数的影响,信噪比在-8~8 d B时,3种算法的分离效率都较低,且分离效率达到100%的速度也落后于第1组。然而,MC_MAP算法曲线可以保持上升趋势,并没有因信道系数的影响与K⁃means算法和One⁃Pro算法曲线在分离效率上升过程中发生类似波动。 图11 第1组信道系数下各算法分离效率Fig.11 Separation efficiencies of the three algo⁃rithms under the first group of channel coef⁃ficients 图12 第2组信道系数下各算法分离效率Fig.12 Separation efficiencies of the three algo⁃rithms under the second group of channel co⁃efficients 图13,14给出了将各算法嵌入到ALOHA随机多址所得到的吞吐量,其中在ALOHA中帧长和标签数均设为128,当标签发生冲突时则执行冲突分离解码算法。此外,图13,14中还给出了未采用分离型冲突分解的纯ALOHA系统吞吐量,其吞吐量接近理论值0.367[21]。由图13,14中显示,当信噪比逐渐增大时,各分离型冲突分解算法的吞吐量均大于纯ALOHA系统吞吐量[15]。即使在两组不同信道系数的影响下,系统吞吐量也大于纯ALOHA吞吐量,且MC_MAP算法吞吐量同样高于One⁃Pro算法,但低于K⁃means算法。与分离效率曲线图类似,在信道系数的影响下,曲线仍然可以保持上升趋势。 图13 第1组信道系数下各算法的吞吐量Fig.13 Throughputs of each algorithms under the first group of channel coefficients 图14 第2组信道系数下各算法的吞吐量Fig.14 Throughputs of each algorithm under the sec⁃ond group of channel coefficients 图15给出了在第1组信道系数下各算法计算得出的各簇中心点与期望中心点的误差,该误差值可反映算法的聚类准确度。从图15中可以看出,MC_MAP算法的误差跟随信噪比的增加逐渐接近于零,准确度在高信噪比时比较高。K⁃means算法的准确度在低信噪比下优于MC_MAP算法,但在高信噪比时二者相似。One⁃Pro算法由于只是一维坐标,误差值起点有起伏,22 dB后才逐渐趋于零,算法准确度较低。综合各算法四簇误差来说,MC_MAP算法的误差范围波动是最小的,可得到较准确的聚类准确度。 图15 各算法计算出的各中心点与期望中心点的误差Fig.15 Errors between the center point calculated by the three algorithms and the expected center point 表5给出了同一信噪比下各算法计算1次中心坐标点所需的平均运行时间,从表5中可以看出,One⁃Pro算法平均运行时间在三者中最短,MC_MAP算法比K⁃means算法平均运行时间少1 ms。因此在相同信噪比下,MC_MAP算法的时间复杂度高于One⁃Pro算法,但低于K⁃means算法。 表5 各算法运行时间Table 5 Running time of each algorithm ms 本部分的实测数据由USRP平台产生,图16给出了当阅读器与标签通信时截取一段RN16作为冲突信号,其信号幅值为计算实部和虚部构成复数的模[15]。由于实测数据中信道系数未知,因此实验结果中未给出各算法实际中心点与期望值中心点的误差。图17给出了实测数据下本文算法在不同网格大小下的性能指标,运行时间T f定义为各算法计算一次聚类中心点平均运行时间以衡量算法的复杂度。从图17中可以看出,网格越大,算法平均运行时间越少,但算法的准确度会降低,误码率也会随之增大,最终影响系统吞吐量。需要注意的是,当网格为0.02×0.02,步长为3个方格时,此时网格过大,MC_MAP算法无法找到正确聚类中心点。综合各个性能指标来看,网格为0.01×0.01,步长为两个方格时,MC_MAP算法计算得出聚类中心点为最佳,此时,该算法可使系统吞吐量达到0.55,相比达到相同解码性能的K⁃means算法,性能指标见表6,本文算法运行时间节约了1 ms。One⁃Pro算法虽运行时间最短,但聚类准确性低,吞吐量只有0.366,接近于纯ALOHA系统吞吐量理论值。 图16 双向通信下阅读器捕获的波形Fig.16 Waveform captured by reader in bidi⁃rectional communication 图17 实测数据下MC_MAP算法不同网格大小的性能Fig.17 Performance of MC_MAP algorithm with different mesh sizes based on measured data 表6 实测数据下各算法的性能指标Table 6 Perfor mance indexes of the two algorithms under the measured data 针对RFID标签冲突问题,本文研究了聚类对冲突标签分离和解码的影响,提出了MC_MAP聚类方法。在仿真实验中,设置了两组不同的信道系数,其中一组信道系数所得到的聚类中心在实轴或虚轴方向有投影重叠。实验结果表明,无论何组信道系数,本文算法均有较准确的聚类准确度,相反,一维投影算法在有重叠的一组信道系数中无法得到所有聚类中心。K⁃means算法也能计算出准确的聚类中心点,并且在低信噪比时就能达到较好的聚类性能,但是该算法复杂度较高,运行时间较长。此外,本文算法虽然在高信噪比下才能达到与K⁃means算法相近的聚类性能,但算法的时间复杂度低于K⁃means算法,这点从实测数据实验结果中能得到反映。因为所用的实测数据信噪比较高,所以本文算法达到了与K⁃means算法相似聚类性能,但运行时间远低于K⁃means算法,最终可使系统吞吐量到达0.55。另外,网格大小对本文算法的性能指标也有所影响,适当的网格大小可提高算法的准确度,减少算法运行时间。 本文算法虽在低信噪比下聚类性能有所减弱,但实验结果表明,信噪比在12 dB以后,本文算法的适用性和时间复杂度将是两种传统算法的折衷,因此在信噪比较高情形下,本文MC_MAP算法可成为标签冲突中聚类分离的候选方案。另外,在实测数据中把从USRP平台所采集的数据送至MATLAB软件中进行处理,以此评判各算法性能,更完整的工作应是将算法直接嵌入至USRP平台,完成测试,这将在未来中进一步完善此工作。3.2 MC_MAP聚类



3.3 信号分离
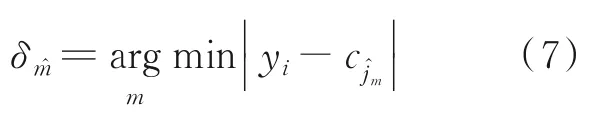
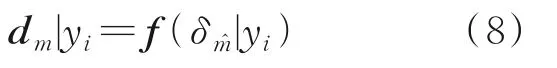
4 实验设置
4.1 数据来源


4.2 实验算法
4.3 性能指标



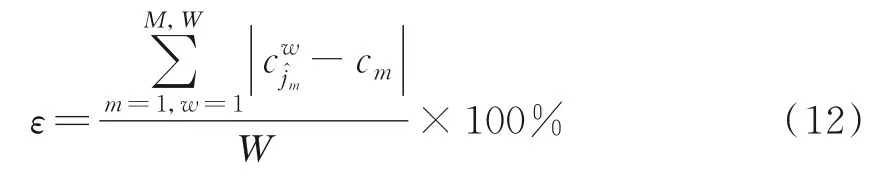
5 实验结果与分析
5.1 仿真数据







5.2 实测数据

6 结束语
