基于特征融合的通信辐射源个体识别
2022-12-13刘志文郑恒权
刘志文,陈 旗,郑恒权,满 欣
(海军工程大学电子工程学院,武汉 430033)
引 言
辐射源个体识别(Specific emitter identification,SEI)是指利用特殊的信号处理手段,结合分类算法、机器学习和深度学习等技术,对侦收到的辐射源信号进行细微特征的提取分类,以达到区分不同辐射源个体的目的。而通信信号与雷达信号由于技术参数存在很多的共同点,从而导致通信辐射源个体之间差异很难直接从接收信号中提取[1]。因此,近年来关于通信辐射源个体识别技术的研究逐渐成为一个研究热点。
现有的辐射源个体识别研究大多是基于单一信号特征,主要是针对所采集到的暂态信号和稳态信号进行。Yuan等[2]对提取的暂态信号进行希尔伯特‑黄变换(Hilbert‑Huang transform,HHT)得到时频能量分布,并提出了13种指纹特征用于个体的分类识别,取得了较好的识别效果。贾济铖等[3]通过采集对讲机的开关机信号,提取暂态信号的围线积分双谱值作为辐射源的特征向量,在此基础上实现通信辐射源的个体识别。暂态信号的优点是包含了丰富的个体细微特征,但是缺点也很明显,即采集相对困难,对噪声比较敏感,抗噪性能差,在非合作通信中的适用性大打折扣[4]。稳态信号是指通信电台工作稳定后所发射的信号,比暂态信号更容易被侦察接收,且受噪声干扰影响较小,具有更好的稳定性,因此是辐射源识别的研究重点[5]。基于稳态信号特征的研究主要针对信号的时域特征[6]、时频特征[7‑8]、高阶谱特征[9‑10]和信号变换特征[11‑13]等进行。文献[6]通过对信号I/Q路矩阵进行拼接,得到IQ图特征,利用卷积神经网络在图像识别方面的突出能力确定辐射源个体。该方法实现简单,具有较强的实用性,但是在噪声较强的情况下识别率不高。文献[7‑8]使用传统的时频分析方法如Wigner‑Ville分布、Choi‑Williams分布以及小波变换等,这些方法都是通过基函数对信号进行处理,在基函数的选择上存在人为主观影响,对于通信信号容易产生交叉项干扰等问题。文献[9]提取矩形积分双谱(Square integral bispectra,SIB)特征参数,在较低信噪比的情况下也能取得较高的识别率。文献[10]提出巴氏距离选择双谱和改进的矩形积分双谱两种算法,对实测通信辐射源进行个体识别,验证了所提方法在鲁棒性、稳定性和复杂度方面的优势。文献[11]通过对信号进行Hilbert‑Huang变换得到Hilbert谱,提取Hilbert谱中的特征作为辐射源指纹特征,从而对辐射源进行个体识别。但是Hilbert‑Huang变换中的经验模态分解(Empirical mode decomposition,EMD)变换存在端点效应,且计算复杂度较高。文献[12‑13]使用固有时间尺度分解(Intrinsic time‑scale decomposition,ITD)的方法对信号进行分解,该方法克服了EMD存在的缺陷,更适合于非线性非平稳信号的分析。但是上述方法为人工提取信号时频能量谱图的细微特征,存在泛化能力差,效率低的问题。
在实际通信场景,尤其是非合作通信的情况下,电磁环境复杂,信号状况多变,单一的信号特征在体现辐射源个体之间的细微特征方面有所欠缺,导致个体识别准确率受到局限[14]。基于以上讨论,本文采用特征融合的方式,对信号进行短时傅里叶变换(Short‑time Fourier transform,STFT)和双谱变换提取时频特征及高阶谱特征,通过小波变换融合技术实现特征融合,达到特征优势互补的目的,而后输入残差神经网络ResNet进行特征提取与分类识别。
1 基于特征融合的个体识别算法
1.1 算法流程
SEI研究在本质上是一个对信号进行分类的过程,对接收端所采集的信号数据进行预处理后,通过特定的变换得到信号特征,提取这些特征的细微差异,从而实现信号的分类。本文基于特征融合算法实现通信辐射源个体识别的过程主要包括5个部分:数据预处理、特征提取、特征融合、细微特征提取和分类识别,整体流程图如图1所示。

图1 算法流程图Fig.1 Algorithm flowchart
首先对采集的短波通信信号进行预处理,裁剪掉信号数据中存在的无信号部分和噪声数据,并进行分段处理。对处理过的通信信号进行STFT和双谱变换得到时频特征和双谱特征,利用小波融合技术进行特征融合。由于残差神经网络具有更深层次的网络结构,能够挖掘更细微的特征,并且解决了网络退化、梯度爆炸等问题,故本文采用残差神经网络进行细微特征提取与分类识别。
1.2 特征提取算法
1.2.1 短时傅里叶变换
STFT作为一种经典的时频分析方法,具有原理简单、适用性好且能够充分体现通信信号时频特性的优点。STFT通过在时间轴上滑动窗函数,截取窗内的信号片段来表示某一时刻的特征。不仅体现信号在瞬时的频率特性,又能体现频率特性随时间的变化。
短时傅里叶变换的定义为
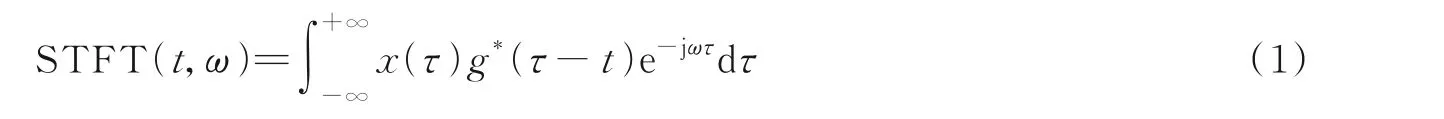
式中:x(t)为源信号,g(t)为窗函数。
1.2.2 双谱变换
高阶累积量和多谱不仅能够抑制高斯噪声,还保留了通信信号的幅度和相位信息,并且与时间无关[15]。其中双谱作为三阶累积量,既具有高阶累积量的优点,且计算较为简单,在通信辐射源个体识别研究中得到了广泛的应用。
假设接收到的通信辐射源信号为x(t),其随机序列为{x(n),x(n+t1),…,x(n+tk-1)},且k阶累积量的Ck,x(τ1,τ2,…,τk-1)满足绝对可求和的条件,即

信号的k阶累积量的k-1阶离散傅里叶变换表示为
当k=3时,三阶谱(双谱)Bx(ω1,ω2)表示为

式中C3,x(τ1,τ2)为信号的三阶累积量。
1.3 小波融合算法
小波变换(Wavelet transform,WT)相比于STFT最显著的特点就是可以根据不同信号频率来自适应地改变窗口面积[16]。设ψ(t)∈L2(R),其傅里叶变换为ψ̂(ω),在信号连续情况下,∀f(t)∈L2(R)小波变换的逆变换都可以表示为
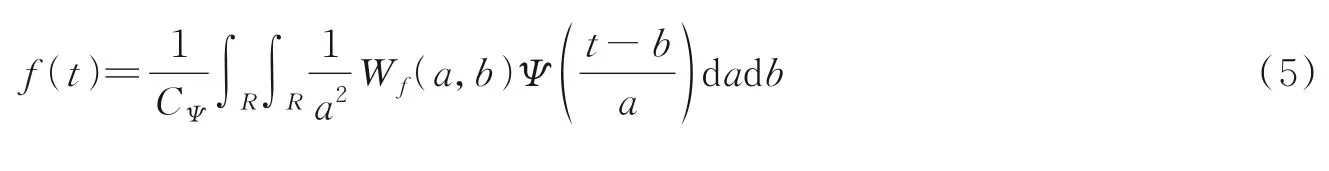
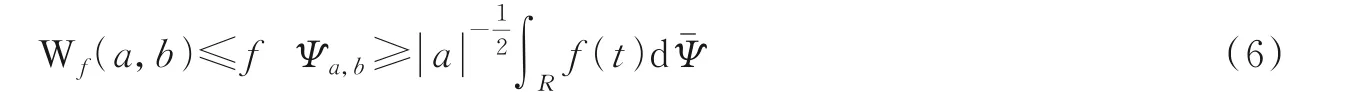
算法流程图[17]如图2所示。由图2可见,在小波融合过程中,首先对输入的各个特征数据分别进行离散小波变换(Discrete wavelet transform,DWT),然后对各分解层分别进行融合处理;最后对融合后的小波金字塔进行小波逆变换,得到重构后的新特征。在此过程中,融合规则和融合算子的选择对最终的融合质量至关重要。针对通信信号这样的高频信号,通常选择使用区域特性量测及加权平均算子。
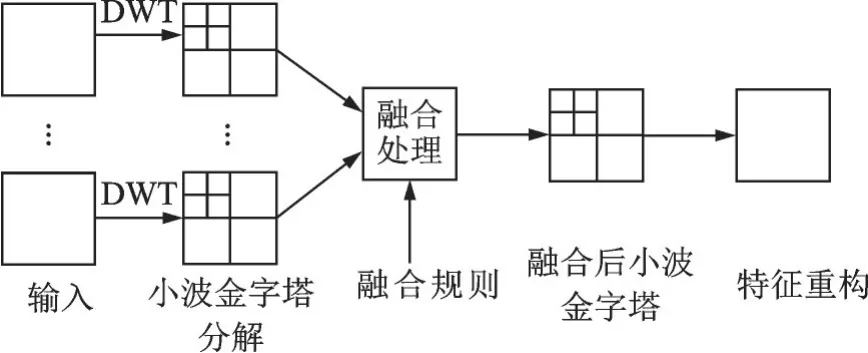
图2 小波变换融合算法流程图Fig.2 Wavelet transform fusion algorithm flowchart
1.4 残差神经网络设计
近年,深度学习已经被证明在各种应用中都有效,特别是在识别方面。具有非线性逻辑功能的多重隐藏层,可以学习隐藏在数据中的更高层次的信息[18]。在现有SEI研究中,卷积神经网络(Convolution‑al neural network,CNN)是一种最常用的神经网络。经典的CNN随着模型深度的增加,其性能也会有相应的提高。但是如果一味地增加网络层数,容易出现梯度消失、网络退化等问题,限制了其网络性能,而残差神经网络可以很好地解决这一问题。残差网络的基本结构如图3所示。

图3 残差神经网络基本结构Fig.3 Basic structure of residual neural network
本文采用50层的残差神经网络,网络结构如表1所示。残差神经网络模型结构为1层卷积层,1层最大池化层,4个残差块,1层平均池化层和1层全连接层。设置激活函数为ReLu函数,学习率为自适应型,优化算法选择Adam算法。网络经过公开数据集ImageNet进行预训练,调整网络参数,以减少网络过拟合的问题,提高网络的适用性。
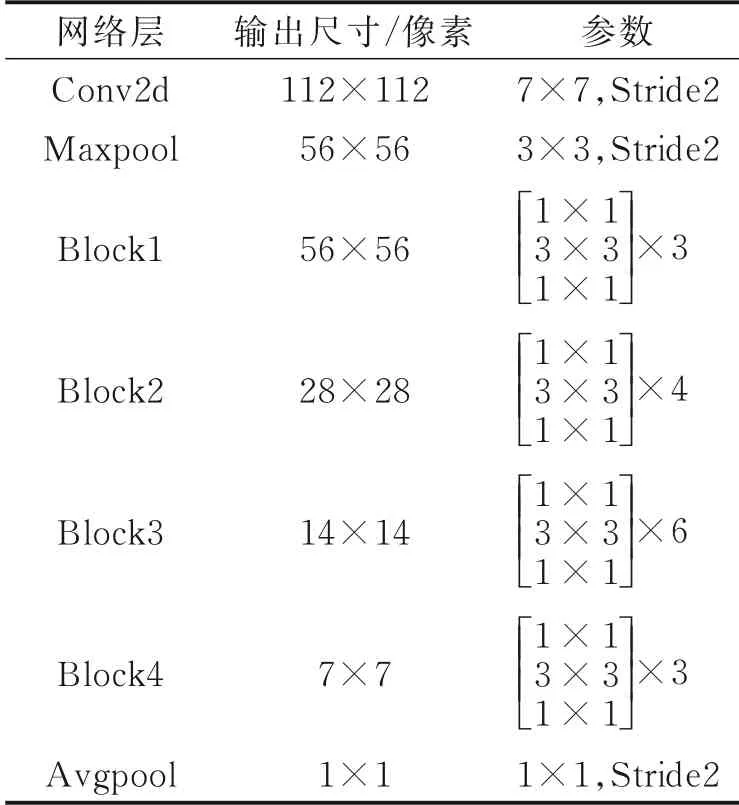
表1 残差神经网络结构Table 1 Structure of residual neural network
2 实验测试与结果分析
2.1 实验参数与数据处理
为了使本文中提出的算法更贴合实际应用,本文使用的通信信号为实际采集两种型号的7部模拟信号源发送的短波通信信号,其中,4部模拟信号源为型号1,编号为辐射源A、B、C、D;3部模拟信号源为型号2,编号为辐射源E、F、G。信号中心频率为8 MHz,信号带宽3 kHz,调制方式都为单边带调制,信号采样率为50 kHz。信号采集地点为室内,以模拟较为理想的通信环境。为了对比算法在不同信噪比(Signal‑to‑noise ratio,SNR)情况下的识别性能,后期通过仿真软件对采集到的信号加入全频段[19]高斯白噪声以模拟不同信噪比下的噪声环境。
实验仿真环境运行在Windows10系统上,计算机处理器为AMD Ryzen 9 5900X 12‑Core Processor 3.69 GHz,RAM 32 GB,显卡为NVIDIA GeForce RTX 3080 Ti,显存12 GB。信号处理、特征提取及融合的编程环境为Matlab 2020a,深度学习环境为Python 3.6,神经网络的搭建采用Pytorch框架。
在通信侦察领域,接收方面对的通信信号往往不是连续发送的,不能保证信号接收的连续性和完整性,尤其是非合作通信的情况下,电磁环境复杂,信号状况多变,受信道特性干扰、接收机自带滤波功能和人为操作不当等影响,接收到的信号存在空白信号、噪声污染等问题,数据预处理的目的就是减少这些问题对辐射源个体识别的影响。本文数据预处理过程为对采集的短波通信信号使用Adobe Audi‑tion2020软件手动裁减掉信号中受接收机影响导致的无信号数据和因接口接触不良、操作不当导致的噪声信号数据,并将每50 000个采样点作为一个信号样本。
本文STFT选择窗函数为Hanning窗,设置窗口长度为256,重叠长度指定为128个点,快速傅里叶变换(Fast Fourier transform,FFT)长度设置为和窗口长度相等的256。设置双谱算法的滞后数为21,每个片段样本数为512,重叠百分比为0,无偏移量,FFT长度为256,窗口为具有单位值的六边形窗口。设置小波分解层为4,小波基为Haar,融合规则为在高频系数中取输入绝对值大的小波系数,在低频系数中取平均值,进而生成一个新的系数矩阵,最后利用新的系数矩阵进行小波逆变换重构出融合后的新特征。
2.2 实验结果及对比分析
2.2.1 特征融合算法测试
输入网络的训练数据集为7部模拟信号源的融合特征图,每台辐射源取600个训练样本,200个测试样本,总共4 200个训练样本,1 400个测试样本。残差神经网络训练次数为50次,Batchsize设置为16,初始学习率设置为0.000 01。ResNet对7部模拟信号源融合特征训练集的训练准确率与损失值如图4所示。
由图4可以看出,随着训练迭代次数的增加,网络的识别准确率迅速上升,损失值Loss迅速下降,并在20轮之后逐步趋于收敛。网络训练结束后,保存网络模型,调用保存好的网络模型对测试集进行测试,得到测试混淆矩阵如图5所示。本文取训练过程中收敛后的10次准确率平均值作为训练准确率,测试准确率为个体识别准确率如表2所示。

表2 辐射源个体识别准确率Table2 Accuracy of specific emitter identification %
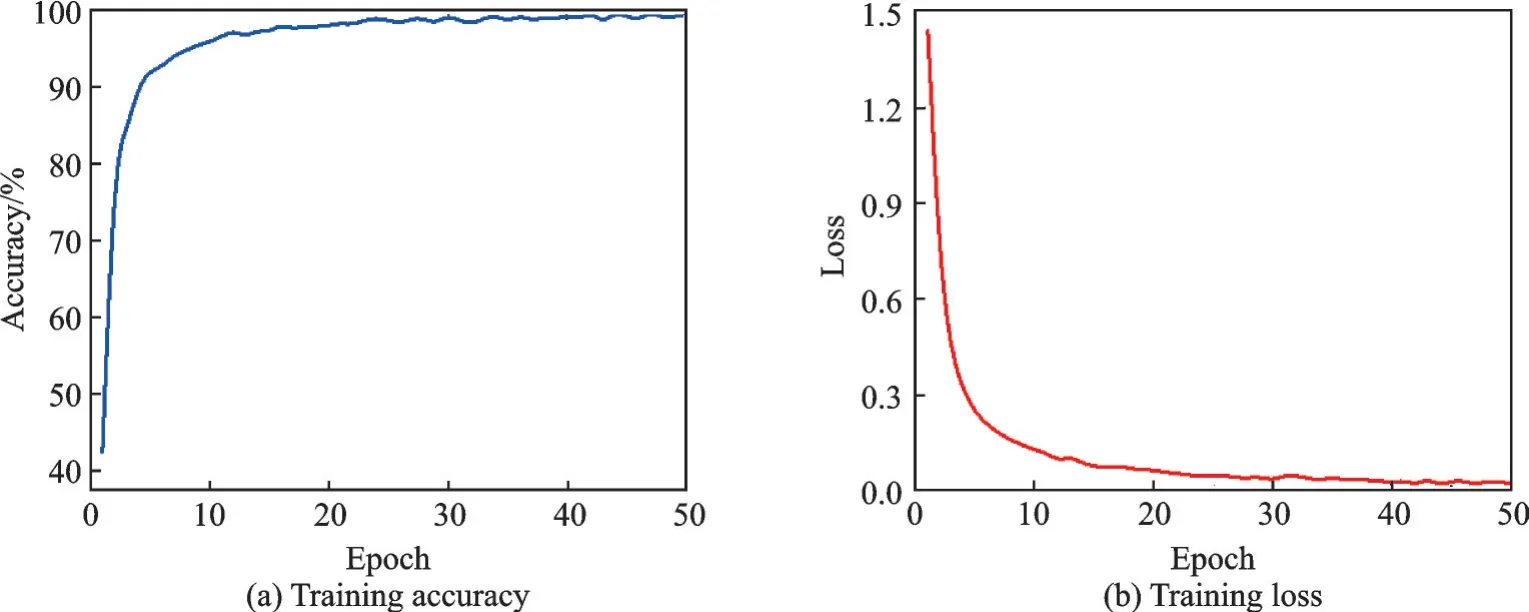
图4 训练结果Fig.4 Training results
通过图5可以看出,ResNet对于经过特征融合后的7部模拟信号源个体有着较好的识别效果。信号源A、C、D、E、G能够完全区分开,信号源B有一小部分被错误分类为A和D。分析原因可能是信号源B的融合特征与A和D存在一定的相似程度,导致网络对B存在误识别的情况。信号源F有一个数据被错误识别成E,分析原因可能是偶然事件导致误识别。总体来说,本文提出的特征融合算法在不加噪声的理想情况下对两种型号的共7部模拟辐射源有着较好的识别能力。
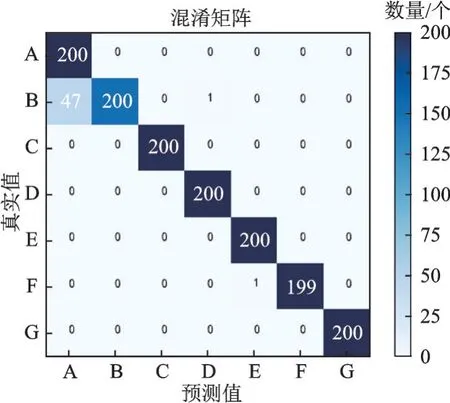
图5 测试混淆矩阵Fig.5 Test confusion matrix
2.2.2 对比实验结果及分析
文献[7‑8]通过提取时频特征,如Wigner‑Ville分布、Choi‑Williams分 布(Choi‑Williams distribution,CWD)、WT等特征对辐射源个体进行识别。由于Wigner‑Ville分布存在严重的交叉项干扰,Choi‑Williams分布可以抑制交叉项,故本文选择Choi‑Williams分布特征和小波变换特征进行对比实验。通过提取7部模拟信号源的Choi‑Williams分布和小波变换特征,分别将其与双谱进行特征融合,与本文提出的STFT‑双谱融合算法进行对比实验。同时,比较单独使用Choi‑Williams分布、STFT、小波变换和双谱变换作为特征的个体识别实验,得到的识别结果如表3和图6所示。算法的耗时程度可以从侧面反映该算法复杂度和计算量的大小[20],因此,记录进行特征融合过程的平均耗时,和单独使用各个算法在处理信号样本时的平均耗时,如表3所示。
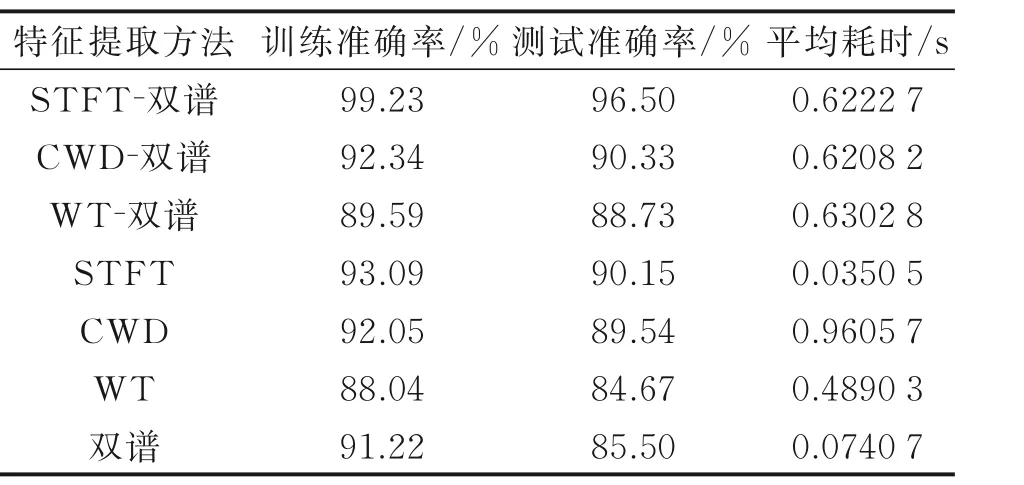
表3 识别准确率Table 3 Accuracy of identification
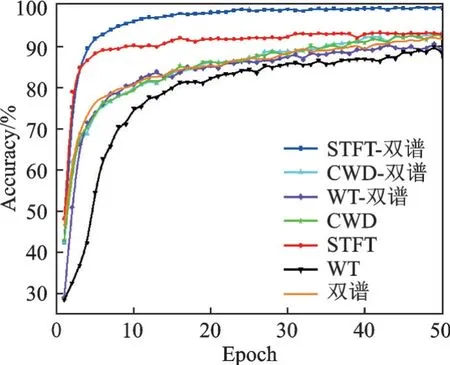
图6 不同特征训练结果Fig.6 Training results with different features
通过对比实验可以看出,本文提出的特征融合方法对于7部模拟信号源个体识别的准确率最高。且融合后的识别率高于单独使用ST‑FT和双谱的识别率,是因为STFT能够体现模拟信号源发射信号的时频特征,双谱能够体现模拟信号源发射信号的幅度与相位特征,单一特征对于不同辐射源存在的细微特征差异的表征能力有限,将STFT与双谱进行特征融合,可以更全面地体现出不同个体之间存在的细微特征差异,从而提高了对7部模拟信号源个体识别的准确率。可以看出,经ST‑FT与双谱进行特征融合的识别率高于CWD和WT分别与双谱进行特征融合的识别率,分析原因是因为单独使用ST‑FT的识别率高于单独使用CWD和单独使用WT的识别率,说明STFT更能提取本文使用的模拟信号源的时频特征差异,并且CWD和WT分别与双谱进行特征融合后也在一定程度上提高了个体识别准确率,从而证明特征融合算法的有效性。通过算法的平均耗时可以看出,使用3种不同的时频分析方法和双谱进行特征融合,平均耗时程度相似,说明小波融合算法的算法复杂度与输入图像数据的类型无关。单独使用STFT的平均耗时最低,单独使用双谱次之,单独使用CWD的平均耗时最高,说明本文提出的STFT结合双谱的特征融合算法的算法复杂度从整体上要优于使用其他方法。通过图6可以看出,使用不同特征开展残差神经网络的训练时,本文使用的STFT‑双谱进行特征融合的算法收敛速度最快,并且保持着最高的准确率,单独使用STFT的训练收敛速度和准确率次之,说明STFT与双谱进行特征融合,从一定程度上提升了使用单一特征的训练速度和准确率。
接下来对信号进行加噪处理,开展验证实验。对采集的短波通信信号添加SNR取值区间为[-15,15]dB,递进5 dB的全频段高斯白噪声,利用特征融合算法进行处理,按照上述参数对网络模型进行训练,测试算法在不同SNR下的性能,识别结果如表4。表4对本文提出的算法在不同SNR下的识别准确率进行了对比实验,可以看出,随着SNR的增加,本文提出的特征融合算法对模拟信号源的个体识别准确率也在不断增大。在15 dB的SNR下识别准确率有93.29%,仅比理想情况下的识别准确率96.50%低3.21%。在0 dB的SNR下识别准确率仍有82.43%,在低SNR的情况下仍有较好的识别性能。

表4 不同SNR下的识别结果Table 4 Recognition results with differ ent SNRs
3 结束语
本文提出了基于特征融合的通信辐射源个体识别方法,通过对所采集的短波通信信号进行STFT和双谱变换,提取辐射源的时频特征和双谱特征,结合小波融合技术进行特征融合,输入残差神经网络进行训练,得到最终的分类结果。实验结果表明,本文提出的特征融合技术与其他相关SEI研究所用的单一特征的方法有着更高的识别准确率,STFT与双谱进行特征融合能够更充分地体现通信辐射源个体细微差异。同时,通过SNR实验可以看出本文提出的算法在低SNR的情况下仍有较好的识别性能。
