改进GA⁃BP神经网络的无线信道预测方法
2022-12-13王智宁彭潇祺
王智宁,江 虹,彭潇祺
(1.西南科技大学信息工程学院,绵阳 621000;2.南洋理工大学电气与电子工程学院,新加坡 639798)
引 言
无线信道预测对无线通信的规划、运行与优化具有重要作用。在电磁波和几何光学等理论的支撑下,射线跟踪(Ray tracing,RT)算法是一种充分考虑电磁波和周围环境相互作用的确定性预测模型,是电磁波传播预测的重要方法。但为了保证RT算法的精确性,需要保证必要的射线发射数量、最大反射次数与最大绕射次数,这带来了巨大的计算量,虽然射线跟踪算法的加速方法层出不穷[1‑2],但对算法效率的提升仍为有限。
神经网络已成为无线通信领域的研究热点[3]。文献[4]提出一种基于反向传播神经网络(Back propagation neural network,BPNN)的三维无线信道特征预测模型。通过对比传统融合信道模型与BP神经网络模型,表明反向传播(Back propagation,BP)能快速预测无线信道特性。但其没有涉及BP结构,该网络在训练优化时易陷入局部最优解的情况。文献[5]基于神经网络,利用基站特征和用户特征的相关性,对基站特征进行训练,以预测用户侧的特征参数。文献[6]提出一种基于机器学习算法和卷积神经网络的信道特性预测方法,当获取收发节点的三维位置信息时,可对室内场景中的子信道进行统计特性的预测,但未考虑预测比室内空间更小的空间环境。文献[7]提出一种模块化神经网络的场强预测模型,基于射线跟踪软件计算的理论值训练神经网络,通过神经网络模块化以及预测数据模块化的方式进行无线信道参数的预测。文献[8]改进了射线跟踪算法,对比了仿真所得路径损耗和BPNN拟合所得路径损耗,验证了BP神经网络算法能够很好地对无线信道参数进行预测。文献[9]基于少量实测数据,构建了基于人工神经网络的路径损耗预测模型,与传统Log‑distance模型进行对比,证明了其模型的优越性。文献[10]通过多层感知器神经网络估计信道中的莱斯K因子,实验结果表明该方法对于莱斯K因子具有很高的精度。文献[11]采用线性回归,支持向量机和深度神经网络来预测眼图指标,数值结果表明向量机和深度神经网络回归都能够捕获收发射机模型在高速信道中所产生的非线性特性。
由上述可知,相较于其他神经网路,BP神经网络具有更好的非线性映射能力、更为强大的自适应和自学习能力,作为目前较为流行的一种算法数学模型,已在多种领域被证实上述能力,非常适用于求解内部机制复杂的问题。传统射线跟踪算法进行场景精确建模具有较大计算复杂度,而将BP神经网络模型与射线跟踪算法相结合进行无线信道预测,既能够将两者的优点相综合,又能够有效地克服现存射线跟踪算法的一些缺点。
BP神经网络本质上仍然是基于梯度下降思想的搜索算法,其本身存在不足之处,诸如易陷入局部极值点、全局搜索能力差等缺点。许多学者做了大量研究以克服这些缺点,有代表性的是蚁群算法[12]、粒子群算法[13]和传统遗传算法[14]等。但上述算法均存在不同缺点,其中蚁群算法寻优盲目,收敛较慢,易陷入局部最优解;粒子群算法后期较难保持种群多样性,同样较易陷入局部最优解;传统遗传算法易早熟收敛,在后期收敛较慢。
鉴于此,基于RT进行信道仿真生成数据集,将信道参数预测模型建模成一个基于BP网络的信道参数预测模型,通过改进遗传算法(Genetic algorithm,GA)优化BP中的权值和阈值来提升BP的全局搜索能力和收敛效率。该模型的优点在于:(1)基于电磁波理论的RT算法进行信道建模仿真所产生的数据精确性高;(2)结合神经网络进行无线信道参数预测,能极大提高信道预测的效率;(3)改进GA对BP网络进行优化,能有效改进局部最优以及种群早熟等缺陷。
1 射线跟踪算法
无论4G还是5G,甚至于未来的6G,通过将通信理论与计算机相结合的方法已是解决无线通信问题的一种有用且高效的方法[15‑16]。RT算法通过模拟射线的传播方式,预测电磁波在传播中的有效路径,结合不同的传播机制,计算每条有效路径的特征参数,对接收节点处所有有效传播路径进行矢量和处理,能够有效进行无线信道建模与仿真。
首先,进行高精度的RT仿真实验,得到某场景无线信道特征参数。论文使用文献[17]中的真实场景,通过对比文献数据,验证了RT算法的精确性和正确性。
其次,通过建模仿真数据进行数据预处理。通过RT算法获取收发节点间的有效射线,包括传播路径长度、传播时间等参数。根据电磁波理论计算出各有效射线到达接收点的场强,并通过对接收点处的信号值进行矢量叠加的计算。得出接收点总场强Etotal为

式中:l为有效射线的总数,E i为第i条射线末场的矢量场强,由式(2)计算[18]。
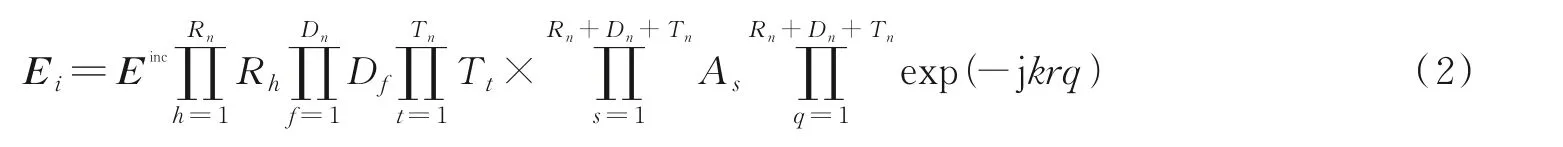
式中:Einc为射线发生下一次传播机制前的矢量辐射场;Rn、D n、T n分别为反射、绕射和透射的总次数;Rh、D f、T t分别为并矢反射、绕射、透射系数;A s为产生各种传播机制后的扩散因子;r q为所跟踪射线发生一次传播机制的距离,q为传播机制节点数。
接收点处的接收功率Pr由接收点的总场强计算,可由式(3)计算[19]。
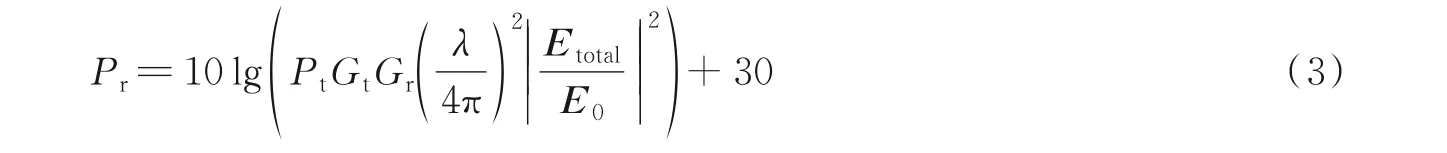
式中:Pt和E0分别为发射功率和电场强度,Gr和Gt分别为收发天线增益,λ为波长。
最后,为了评估所提出的基于多种群遗传算法的BP神经网络性能。论文在目标场景中固定发射点,随机布置接收点,进行该目标场景下的无线信道仿真实验,存储大量标签样本用于BP训练。
2 改进GA⁃BP神经网络的无线信道预测方法
在某场景中,对于一个固定的收发点位置,功率随着收发点间的距离和收发点间障碍物的数量增大而减小,可以看作收发点三维坐标点间的非线性函数。基于此,提出一种基于BP的多输入单输出非线性函数建模方法。BP网络包含非线性激活函数,它将输入信号映射到不同的非线性域。这些非线性域输出与适当的权值相乘,并以一个常数值偏置,使这些输出的总和最终等于所需的输出。
2.1 神经网络算法
BP网络由输入层、隐藏层和输出层3部分构成,每层由相应神经元构成,总体采用单向连接方式,层与层之间实行全连接,并通过梯度下降算法,寻求误差小、预测精准的神经网络[20]。BP网络通过适应度值的调整不断更新网络中的权值和阈值,逼近期望输出值,生成输入和输出的非线性关系函数。然而,BP网络中隐藏层到输出层的连接权值和阈值采用随机取值方法,存在收敛慢、易陷入局部极小值的问题。
2.2 遗传操作
GA可以在不需要误差函数梯度信息的情形下学习近似最优解,从而具备优秀的全局搜索能力,尤其适用于求解复杂的非线性问题求解[21]。GA通过对种群进行遗传、变异、选择以及交叉等操作,筛选出最优个体。
本文将GA中对种群的操作整合成遗传操作。即首先将待优化值转化成二进制编码,以二进制编码为个体构建初始种群,接着依次进行各遗传操作,然后将二进制个体解码成实数个体,转换成可用于BP训练的实数串,最后将完成操作的个体代入BP中迭代计算适应度,寻找适应度最小的个体。本文中的适应度值L由复数场强模的预测值和期望值计算,计算方式如下

式中:m为BP输出节点总数,y i和p i分别为BP网络节点的期望值和预测值。
2.3 基于改进GA的BP神经网络
2.3.1 优化GA‑BP算法构建思想
传统GA能在一定程度上提升神经网络算法的全局搜索能力和收敛速度。然而,传统遗传算法初始种群的产生和遗传操作的执行都具有随机性,导致该算法仍存在收敛慢和易陷入局部最优解的缺点。针对该问题,本文构建了多种群遗传算法。
多种群遗传算法(Multi‑population genetic algorithm,MPGA)的基本思想是:采用多种群并行计算方式,进行多种群同步遗传操作,择取各种群中的最优个体,组成最优种群,再次进行遗传操作,进化出最优个体。由于多个种群间保持相互独立,利用各子种群进行多代遗传操作后的最优个体,重组为最优种群,进行最优基因之间的信息交换,即增加了基因模式数的同时,又保持了最优个体进化的稳定性,还可以通过最优种群进化出更优个体。该方法能增强GA的全局搜索能力,加快算法的收敛效率。
MPGA具体步骤如下:首先,初始化Npop个权值和阈值种群,每个种群中所具有的个体数都相等,并且将个体中的所有权值和阈值组成二进制数串。然后,对各子种群进行遗传操作,进化出子种群中的最优个体。接着,选择各个子种群中的最优个体,组合成最优种群。最后,对最优种群进行遗传操作,进化出最优个体。
2.3.2 数据预处理
射线跟踪算法基于几何理论和一致性绕射理论,能够识别收发节点间的所有有效射线,并计算出无线信道特征参数,如接收场强、接收功率和路径损耗等。
本文通过将收发节点三维坐标值进行归一化处理,组成六元组,作为输入

根据射线跟踪算法计算的无线信道特征参数构成神经网络输出

式中输出参数可分别为接收场强、接收功率和路径损耗等多种无线信道特征参数。
基于射线跟踪算法在目标场景中进行多次仿真,搜集到能够用于训练的数据集。对数据集进行随机选取,按照7∶3的比例分为训练集和测试集,用于神经网络的训练和测试。
2.3.3 构建MPGA‑BP神经网络
基于改进GA优化BPNN算法的流程如图1所示。图1中共有9个步骤,从确定网络拓扑结构到使用BP进行预测,将MPGA与BP进行结合形成新的BP网络模型。整个模型确定所需神经网络结构后,采用MPGA优化BP神经网络,确定初始权值和阈值,输入训练数据集,训练网络,直至当前BP满足精度要求为止。步骤如下:

图1 基于改进GA优化BPNN程序流程图Fig.1 Program flow chart of BPNN optimization based on improved GA
(1)确定网络拓扑结构。本文神经网络中的输入层采用6个神经元,隐藏层由两层全连接层构成,各11个神经元,用h表示;输出层由1个神经元组成,用m表示。
(2)初始化权值和阈值。将BP中的权值和阈值赋值为随机产生的8位二进制数串。
(3)获取最优权值和阈值。通过MPGA优化初始权值和阈值,获取最优值。
(4)计算隐藏层输出。阈值为bh,激励函数为f,输入两层之间的权值为ωij,且采用ReLu函数,输出值为

(5)计算输出层输出。阈值为bo,两层之间的权值为ωjk,输出值为
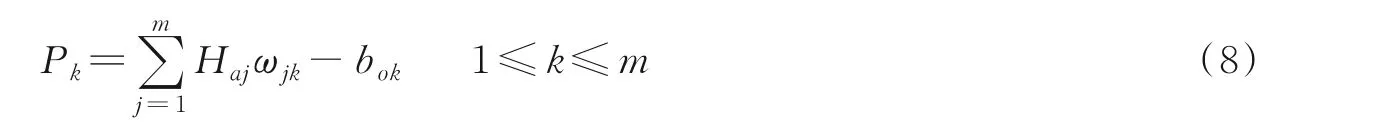
(6)计算误差。误差e为预测值和期望值之差,计算方式如下

(7)更新权值和阈值。根据上述步骤计算出误差e,更新ωij和ωjk,计算方式如下
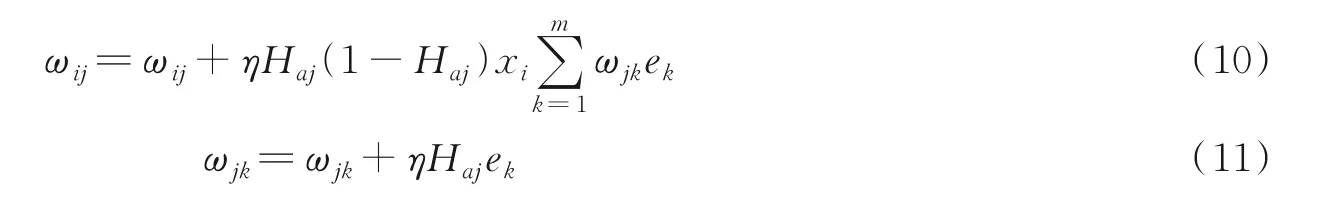
式中η为学习速率,本文中设置为0.1,阈值修正计算如下
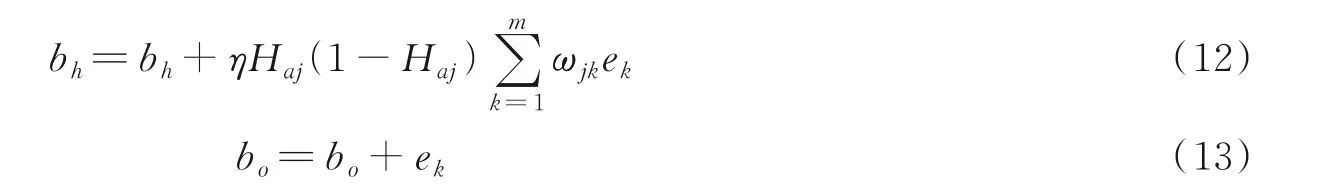
(8)对网络误差进行判断。若误差满足要求,则达到结束条件。否则,回到步骤6继续学习。
(9)测试数据,进行预测。神经网络达到预期设定后,对当前神经网络模型进行保存,然后进行预测。
2.3.4 多种群遗传算法收敛性分析
为便于MPGA算法收敛性分析,本节使用符号定义如下。
符号1:种群大小和空间分别为Psize和SN,个体染色体长度为l,种群迭代次数为n。
符号2:使用大写表示当前种群,如X。
符号3:使用小写和下标表示当前种群个体,如x i。
符号4:使用f(·)表示个体的适应度值,如f(x i)表示种群X中个体i的适应度值。
各算子符号的定义如下。
(1)选择算子Ts
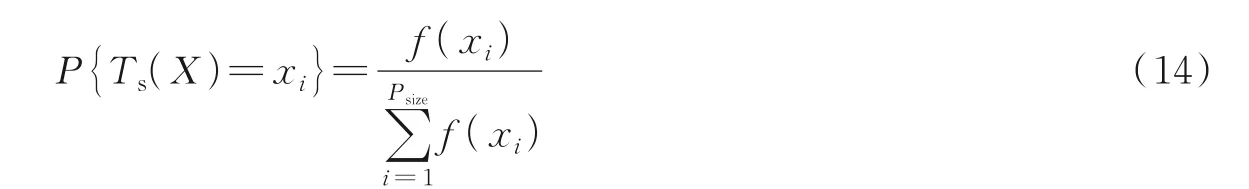
(2)交叉算子Tc

式中:Pc为交叉概率,l为杂交点可选择的数量。
(3)变异算子Tm
定义式与Tc相似。
(4)满意值算子Tg

MPGA算法的个体更新过程可表示为

MPGA算法迭代过程可表示为
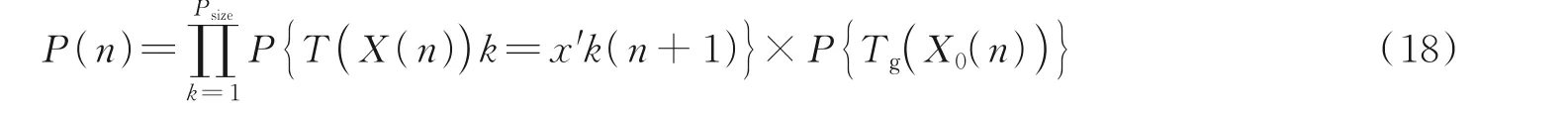
由定义可知,P(Tc)、P(Ts)和P(Tm)均大于0,所以有

由算子Tg定义可知,,证得该算法依概率收敛。
2.4 算法时间复杂度分析
2.4.1 传统GA与改进GA的时间复杂度分析
传统GA的时间复杂度主要来源于对适应度函数的多次调用[22]。通常可以基于遗传算法中间点的染色体编码长度、种群规模和迭代次数来对适应度函数的调用次数进行计算[23]。
结合文献[22‑24],通过分析本文中适应度函数的设计,假设交叉概率为1,可以得出在优化BP神经网络结构问题中,传统GA的时间复杂度为

式中:TGA1为初始化种群个体染色体编码的耗时;TGA2为针对种群进行遗传操作的耗时;Tfit为适应度函数的耗时;Nfit为适应度函数的调动次数;ip为染色体编码长度中间点数目;ps为种群规模;gn为迭代次数。相比于对种群进行遗传操作的耗时,初始化种群个体染色体编码的耗时可以忽略不计。因此,传统GA的时间复杂度为

通过分析改进GA,得到采用改进GA进行BP神经网络优化的计算时长TNGA由以下几个部分构成:(1)时间TNGA1为初始化多种群个体染色体编码;(2)时间TNGA2为对多种群个体并行进行遗传操作的耗时;(3)时间TNGA3为组合最优种群的耗时;(4)时间TNGA4为对最优种群进行遗传操作的耗时。则可知
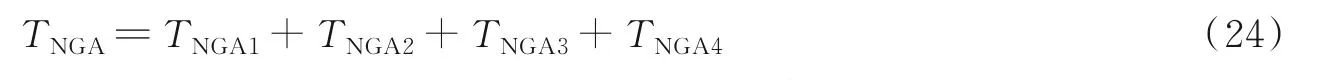
相较于对多种群和最优种群进行遗传操作的耗时,初始化多种群染色体编码和组合最优种群的耗时可以忽略不计。
由于对多种群进行遗传操作是并行进行,所以时间TNGA2和时间TNGA4均可与传统GA的时间复杂度相等。所以,改进GA的时间复杂度为

据式(23,25)可得,改进GA的时间复杂度与传统GA的时间复杂度相等。因此,改进GA算法并未增加算法的时间复杂度。
2.4.2 传统RT与改进BPNN的时间复杂度分析
通过分析传统射线跟踪算法,单根射线完成传播的耗时TRT由以下几个部分构成:(1)时间T1为射线跟踪过程中发生一次传播机制的耗时;(2)时间T2为判断当前射线是否被接收点所接收;(3)时间T3为计算所有有效射线特征参数的耗时。则可知

相较于射线数量,仅需单次计算的T3可以忽略不计。
假设场景中障碍物表面总数为Fall;单次线面求交计算耗时为k1;单条射线从开始到结束发生传播次数平均为Tavr,则时间T1为

T2为判断所跟踪射线是否被接收。假设相关耗时为k2,则时间T2为

相对于T2,T1的耗时更为巨大,因为求交运算、传播机制判断等相关计算的计算过程复杂,而判断是否被接收点所接收的计算过程相对简单,因此k1远大于k2。其次,因为T1同时与整体环境中的物体表面总数为Fall和传播机制的次数Tavr都有关,且物体表面总数Fall与T2无关,并且其值远大于Tavr。因此可以忽略T2,则算法最终时间复杂度TRT可表示为

由于BP神经网络通过适应度值逆向调整各神经元的权值和阈值,且所构建神经网络为两层神经网络,其时间复杂度为

式中S为单层网络中的网络节点数。
由于此两层神经网络隐含层节点数S通过误差和节点数的测试后经人为设定,与传播机制次数Tavr通过衰减计算后的最大值近似,物体表面总数Fall远远大于节点数S和传播机制次数Tavr,且随着场景复杂度的提升,呈现几何级增长。因此TRT≫TBP。由此可得,BP神经网络的预测效率是远优于传统射线跟踪算法的预测效率。
2.4.3 传统RT与改进GA优化BPNN的时间复杂度分析
通过分析改进GA优化BPNN算法,得到整个神经网络训练的时间复杂度TGABPNN为

式中TTBPNN为训练神经网络的时间复杂度。
根据2.4.1和2.4.2节,可得改进GA优化BPNN的时间复杂度为

根据2.4.2节,可得训练神经网络的时间复杂度为

式中∂为训练集的数据数量。
相对于训练集的大小∂,适应度函数的调动次数Nfit可以忽略不计,因此改进GA优化BPNN进而进行BPNN训练的时间复杂度为

由于神经网络训练集的大小∂通常在万级数量以上,因此神经网络训练消耗的时间常是大于单次传统RT算法的。然而,在固定场景中,采用传统RT进行多次无线信道预测的耗时将远大于训练神经网络的耗时。即使训练神经网络有较大的耗时,但换来了在应用该网络进行无线信道预测时更高的效率。
3 仿真结果对比分析
3.1 目标场景
为了验证本文所提出方法的有效性,论文构建场景的三维图形进行建模。该场景为立方体的密闭小空间,上下底半径均为2 m,高为6.5 m,内部分为3层:上层空间中有3个立方体形障碍物模型;中层空间共有6个立方体形障碍物模型;下层空间中有1个圆柱形障碍物模型,整个场景如图2所示。在无线信道仿真中,场景中障碍物材料介电常数为4.5,导电率为0.8 S/m。导出场景STEP文件,将目标场景的形状、尺寸和材质等信息导入仿真平台进行数据解析以及三维建模仿真。
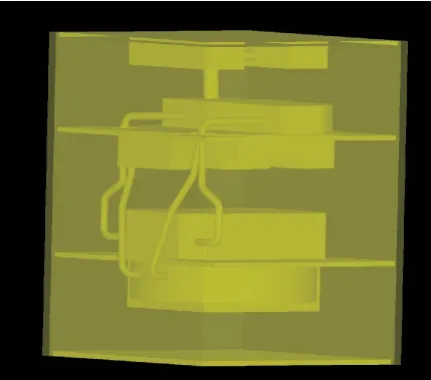
图2 导入系统后的环境模型Fig.2 Environment model after importing the system
3.2 验证BP神经网络算法精确性
首先与RT算法结果进行对比,验证两种BP神经网络模型的精准性。神经网络结构如2.3.2节所述,MPGA设置的种群数为20,单个种群个体数为20,模型训练结束条件为迭代次数达到10 000次。
本次验证的环境模型如3.1节所描述,设定发射频率为1 GHz,收发节点均为全向天线,射线发射数量为4万条。发射点坐标固定为(234,144,352),单位均为cm。仿真使用In‑tel i7处理器,16 GB内存,Qt仿真平台。
图3是GA‑BP神经网络的预测值和期望输出对比图,图4是MPGA‑BP神经网络的预测值和期望输出对比图。从图3可以看出,各测试样点都具有良好的精度,但极个别处的测试样点误差偏大。而图4中MPGA‑BP神经网络模型则具有更高的精度,尤其在一些GA‑BP神经网络效果不好的点。从以上两个对比图中可以看出,MPGA‑BP神经网络模型具有更高的精度,证明了两种BP神经网络模型无线信道预测的精确性。这是因为两种网络的数据集均来自射线跟踪算法仿真数据,而射线跟踪算法是一种充分考虑电磁波和周围环境相互作用的确定性模型,通过大量的射线发射数量和必要的射线传播次数,保证了极高的预测精度。因此两种网络均具有较好的预测精确性。

图3 GA-BP神经网络输出与期望输出对比图Fig.3 Comparison between GA-BP neural network output and expected output

图4 MPGA-BP神经网络输出与期望输出对比图Fig.4 Comparison between MPGA-BP neu‑ral network output and expected output
3.3 验证改进算法有效性
为验证本文所提出的模型的有效性,本节从两方面进行分析。(1)分别将GA和MPGA优化BP网络前后的结构参数进行对比,验证GA和MPGA优化BP网络的有效性。(2)将GA‑BP和MPGA‑BP网络模型应用于无线信道多种特征参数的预测,例如接收功率、路径损耗和时延扩展等参数,通过平均绝对误差、标准差和均方根误差等参数对混合模型的预测能力进行比较,验证混合模型进行无线信道预测的有效性。平均绝对误差的定义为

式中RSSd和RSSp分别表示期望值和预测值。Sn为所预测的样本总数。标准差为

而均方根误差表示为

两种网络都具有两层隐藏层的网络结构,隐藏层神经元个数均为11个,种群交叉概率均为0.7,种群变异概率均为0.05,种群迭代次数均为20。传统遗传算法模型种群个体数为400,多种群遗传算法模型种群个体数为20,种群数量为20。分别预测接收功率、路径损耗和时延扩展。通过将两种网络预测结果的平均绝对误差、标准差和均方根误差进行对比,比较两种网络的预测精确度。
图5,6分别给出了GA和MPGA优化BP网络的结构参数前后对比图。从图5,6可以看出,在经过GA和MPGA两种算法优化后,BP网络中的结构参数均有不同程度的变化。展示了GA和MPGA均具有对BP网络中的结构参数进行优化的能力。图5中部分结构参数并未发生改变,图5中参数的变化程度小于图6中参数的变化程度。这是因为MPGA具有更强的基因交换能力,增强的基因交换能力,能够有效改善种群早熟等缺陷。
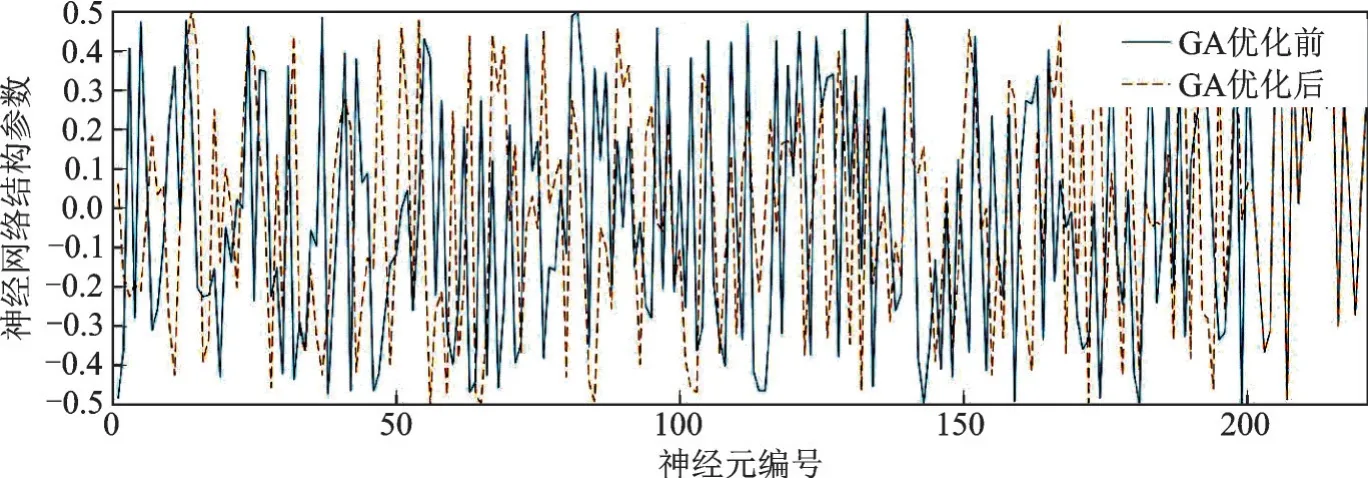
图5 GA优化BP网络前后的结构参数对比图Fig.5 Comparison of structure parameters before and after GA optimization of BP network

图6 MPGA优化BP网络前后的结构参数对比图Fig.6 Comparison of structure parameters before and after optimizing BP network by MPGA
表1~3分别给出了两种模型对于接收功率、路径损失和时延扩展多次实验下的平均预测误差对比。从表1~3中可以看出,无论是接收功率、路径损失还是时延扩展,本文所提出的MPGA‑BP神经网络模型比GA‑BP神经网络模型都具有更高的预测精度,且具有更小的标准差。这是因为MPGA相对于GA拥有更多的基因和基因交流次数,给予了MPGA更强基因交换能力,而具有更强基因交换能力的MPGA的优化能力则更强,进一步提升了模型的预测精确度。就目前所训练的3种无线信道特征参数,本文所提出的MPGA‑BPNN相对于GA‑BPNN都具有更高的预测精度。
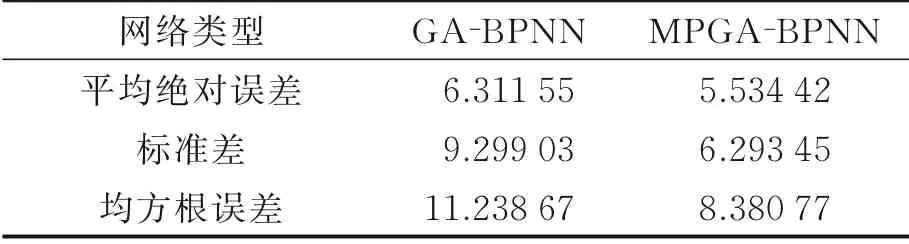
表1 两种模型接收功率预测误差比较Table 1 Comparison of received power prediction err ors between two models dBm
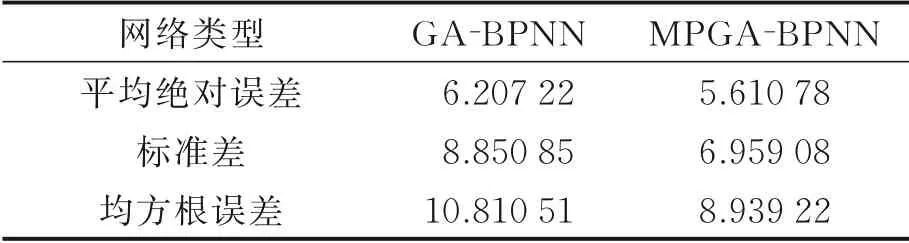
表2 两种模型路径损失预测误差比较Table 2 Comparison of path loss prediction err ors between two models dB
4 结束语
针对传统射线跟踪算法仿真效率低、GA‑BP网络预测精度差的问题,本文改进传统遗传算法,提出了一种基于射线跟踪算法结合BP神经网络的无线信道预测方法。改进遗传算法的全局搜索能力使得神经网络连接权值和阈值得到了更精确的调整,得到了最优的BP网络算法,MPGA‑BP网络能够高精度对无线信道进行预测。通过比较可知,所提出的MPGA‑BP网络相对于GA‑BP网络具有一定的精确度提升,说明了本文模型的有效性。
然而,实验采用训练集和测试集均为仿真数据,缺少实际信道数据,虽然射线跟踪算法已经是很可靠的无线信道预测模型,但仍与实际信道的测量数据存在差别。另外,由于数据集来源于固定场景的无线信道仿真试验,造成该神经网络只能反映目标场景的无线信道特性,更换场景则需重新进行网络训练,普适性较差。因此,下一步的研究方向主要是进行实际环境的信道分析,并采用多场景的无线信道数据进行神经网络训练。

表3 两种模型时延扩展预测误差比较Table 3 Delay spread prediction error comparison of two models s
