尾缘射流式垂直轴风力机气动特性数值分析

2022-12-13李东旭

哈尔滨工业大学学报 2022年1期

李东旭，李春,2

(1.上海理工大学，能源与动力工程学院，上海 200093；2.上海市动力工程多相流动与传热重点实验室(上海理工大学)，上海 200093)

世界能源结构变化使得水能、风能、太阳能、地热能和生物质能等可再生能源成为各国关注重点，其中风能是最具前景的新能源之一[1-3]。进入21世纪，风电技术高速发展极大提高了风能使用率，由此迎来风能开发的新一轮热潮[4-6]。风力发电作为燃烧化石燃料的替代方式，不仅在运行过程中不产生任何温室气体，且几乎不占用耕地资源[7]。

风力机是将风能转换为电能的一种动力装置，其中垂直轴风力机(VAWTs,Vertical Axis Wind Turbines)旋转轴垂直于地面并具有以下优点：1)传动机构位于地面，易于运行及维修[8]；2)叶片重力载荷力矩恒定，不易发生疲劳损伤[9]；3)适用于任何风向，无需偏航装置[10]。尽管VAWTs存在诸多优点，但因其自身固有特性导致叶片有效攻角不可避免地随运行方位角发生大幅变化，致使翼型极易处于失速状态并发生流动分离现象。

流动控制是指针对叶片绕流气体进行人为控制，最终使叶片达到所需技术要求[11]。射流技术因具有结构简单及控制方法多样性等优势，逐渐被应用到风力机叶片的流动控制领域。Ciuryla等[12]通过风洞实验研究机翼射流对流动分离的控制效果，结果表明内侧副翼射流可将分离点向尾缘推迟并减小分离区域。Liu等[13]和Rimasauskiene等[14]研究了不同种类及参数的激励器对射流频率影响，得出所需不同频率下射流激励器相应的最佳输入功率。Bazdidi-Tehrani等[15]通过数值模拟方法研究进口边界条件和射流速度的关系，结果表明，选用运动活塞和滑动膜片两种进口作动方式对射流速度峰值有显著提高作用。Montazer等[16]基于NACA0015翼型，在改进零质量射流装置结构后，得出对射流孔合理优化可使翼型最大升阻比提高约66%的结论。Mcdonald等[17]通过数值模拟发现，合成射流不仅可使圆柱表面阻力系数减小，而且能降低远场尾迹区湍流强度。Yen等[18]通过实验研究，分析了共流射流对水平轴风力机气动性能影响，实验发现，在低尖速比时采用间断性共流射流可有效提高风力机安全稳定性并减小叶尖损失。

射流技术已广泛应用于流动控制领域，但针对垂直轴风力机的相关研究并不多，且大多数研究仅基于静态翼型对升阻力进行分析。本文将尾缘射流技术应用至旋转状态下的垂直轴风力机中，通过数值模拟方法比较不同射流角度对垂直轴风力机气动性能的影响，并对流场控制效果等进行分析。

1 气动性能数值计算

1.1 VAWTs主要气动参数

图1为垂直轴风力机翼型在不同方位角时的受力及速度三角形，翼型攻角表示如下：

(1)

式中：θ为风力机相位角；λ为叶尖速比，为风轮叶片尖端速度与来流风速之比，表示为

(2)

式中：R为风力机旋转半径，ω为旋转角速度，V∞为来流风速。

力矩系数Cm与风能利用率Cp也都是VAWT重要的气动参数，分别为

(3)

式中：A为风力机扫风面积；P为输出功率；T为转矩；ρ为空气密度。

图1 翼型受力及速度三角形Fig.1 Airfoil force and velocity triangle

1.2 垂直轴风力机模型

H型风力机是垂直轴风力机中的典型代表，由于气动性能和结构优势等综合因素，已成为达里厄升力型风力机的研究热点[19]。本文采用H型风力机作为研究对象，其几何模型及参数如图2所示。为与实验结果[20]进行对比，依据表1选取主要参数。

图2 垂直轴风力机几何模型Fig.2 Geometric model of VAWT

表1 垂直轴风力机主要参数Tab.1 Main parameters of VAWT

1.3 尾缘射流方法及模型

吹气射流是一种射流强度可观、实用性较强且应用广泛的射流方法[21]。本文采用定常吹气实现风力机尾缘射流，结构装置如图3所示。气体从叶尖吸入透平式压缩机，由叶轮压缩后流入储气室再经管道从尾缘射流孔处射出。当风力机发生流动分离时，通过叶片表面压力传感器将信号传入压缩机的控制系统，进而结合管道特性调节压缩机功率，实现以40 m/s匀速吹气射流。由于所需气流具有连续稳定、流速较高且流量较小等特点，故选用透平式压缩机。装置中储气室不仅可以降低压缩空气中的水分，平稳管道压力，还可以存储一定量的临时气体以便在突发故障时做应急使用。

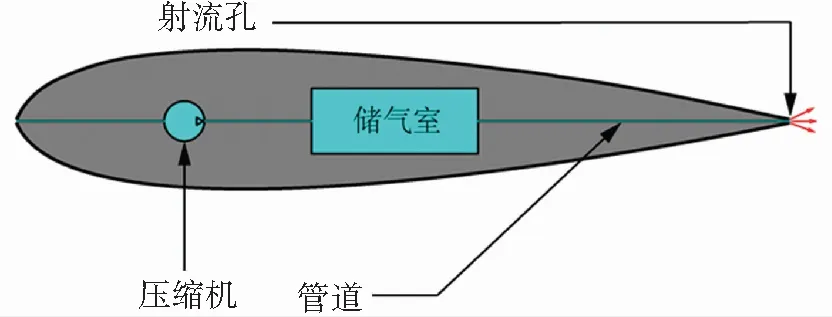
图3 吹气射流装置Fig.3 Device of blowing jet

图4为尾缘射流孔的局部放大图，射流孔中心距翼型尾缘水平距离为D(0.003c)，射流孔径宽为L(0.002c)，射流速度为v(40 m/s)。射流角度φ定义为翼型弦线与过尾缘中点且垂直于尾缘的直线夹角，由于尾缘边界几何参数的限制，φ取-20°到20°之间，且定义射流吹向风轮内侧为负值，相反为正值。

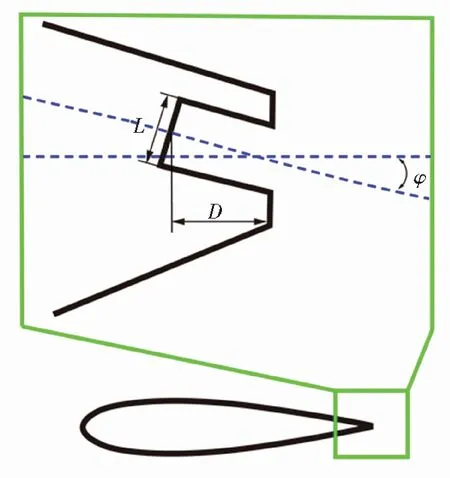
图4 尾缘射流孔位置及参数Fig.4 Position and parameters of trailing edge jet slot

1.4 计算域网格及计算方法

计算域拓扑结构如图5所示，流场计算域被划分为内流域、旋转域及外流域。其中,外流域由半径为10R的半圆形区域和长为20R的长方形区域组成，内流域和旋转域半径分别为0.58R与1.36R。各计算域及翼型附近网格划分如图6所示。

将进口AC边界设置为速度入口，来流风速为9 m/s；出口BD边界设置为压力出口，相对压力为0 Pa；外流域AB、CD两边界设置为wall；其余边界条件为interface。Transition-SST湍流模型在工程需求中应用广泛，且可较为准确地反应宏观流动现象，故选择Transition-SST作为湍流计算方法。使用压力基求解器耦合求解动量方程与连续性方程，为节省计算资源，提高计算稳定性，采用SIMPLE算法，二阶迎风离散格式，收敛误差为10-6。

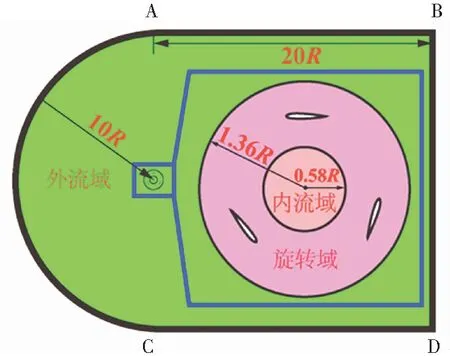
图5 计算域拓扑结构Fig.5 Topological structure of computational domain

(a)外流域网格 (b)旋转域网格

1.5 湍流模型与网格无关性验证

如图7所示为不同湍流模型的实验对比验证。由图7可知，无论是在高尖速比还是低尖速比时，采用Transition-SST湍流模型均能较为准确地计算出所对应的风能利用系数(CP)，其中在λ=3.1时，实验数据[20]与模拟值误差最小，为0.49%，其他尖速比时误差最大不超过5%。因此，本文针对尾缘射流式VAWTs采取的Transition-SST湍流模型合理且可信。

图7 湍流模型验证Fig.7 Verification of turbulence model

表2给出了5种不同密度的计算域网格。由于本文主要针对翼型附近网格进行验证，且需要良好的网格过渡性，所以在翼型网格密度增大的同时旋转域网格数量也随之增多。选取并验证λ=2.63时翼型周围网格数，由表2可知，当网格为G3、G4和G5时，CP的计算偏差很小，并且G5总网格数量是G4的3倍，而计算得到的CP却十分接近，因此综合考虑计算精度与计算资源，选用G4网格用于本文的模拟计算。

表2 网格分布参数Tab.2 Parameter of grid distribution

2 计算结果与分析

图8为不同射流角度下风能利用系数曲线。由图8可知，无射流与有尾缘射流式垂直轴风力机CP曲线变化趋势基本相同，且最佳尖速比均在2.63左右。在较小尖速比时(1.68以下)，-20°射流角度对CP的提升效果优于-10°;而随尖速比逐渐增加，射流角度为-10°的风力机CP接近并超过-20°。因此，增加尾缘负射流角度对CP的影响并不具有线性关系。除λ=1.68、3.30外，10°射流风机的CP优于20°射流风力机的CP，其他尖速比时，10°和20°射流CP基本接近，故增加尾缘正射流角度对CP几乎没有影响。整体上，在尾缘射流角度为0°时的CP明显低于其他射流角度的CP；随尖速比增加，不同射流角度在提升CP能力方面都表现出积极效果，当达到最佳尖速比附近时，0°射流对CP提升效果可达5%左右，其他射流角度提升作用更加明显可到11%左右。在较高尖速比时(大于2.63)，虽然射流式垂直轴风力机CP逐渐降低，但仍高于无射流情况。这说明尾缘射流通过对翼型吸力面边界层提供更多动能，增强叶片表面流体再附着能力，有效抑制流动分离，进而提升风力机气动性能。

图9为无射流与尾缘射流式垂直轴风力机整机力矩系数(Cm)的变化曲线，所有曲线均呈现出周期性变化。由图9(a)可知，在λ=1.68时，无射流风力机的Cm峰值小于除0°射流外所有尾缘射流，且随射流角度的增加，Cm提升效果更为显著；λ=2.63时所有射流方式都对Cm有提升效果且在整个周期内均优于无射流情况，此时CP基本可以提升10%左右，但射流角度为0°时，平均力矩系数与其他角度相比提升较小，因此CP在最佳尖速比附近提升效果仅为5%左右；图9(c)是λ=3.3时不同射流角度的Cm曲线，在整个运行周期内，0°射流角度出现Cm最小值，-20°射流出现最大值，但此时不同射流角度的风力机Cm变化范围基本一致。整体上在λ=1.68时，Cm波动幅度较大，λ=2.63、3.30时，不同射流角度Cm波动幅度较小，但周期性表现上略有差异。在较低尖速比时，尾缘射流角度从-20°增加至20°，除0°射流外Cm均逐渐提高，其中10°射流对Cm提升效果最好。在较高尖速比时，尾缘射流在射流角度从-20°至20°，Cm基本没有变化，此过程Cm对射流角度的敏感程度较低，即尾缘射流对力矩系数影响较小。

图8 不同射流角度下的风能利用系数Fig.8 Wind power coefficient with different angles of trailing edge jet

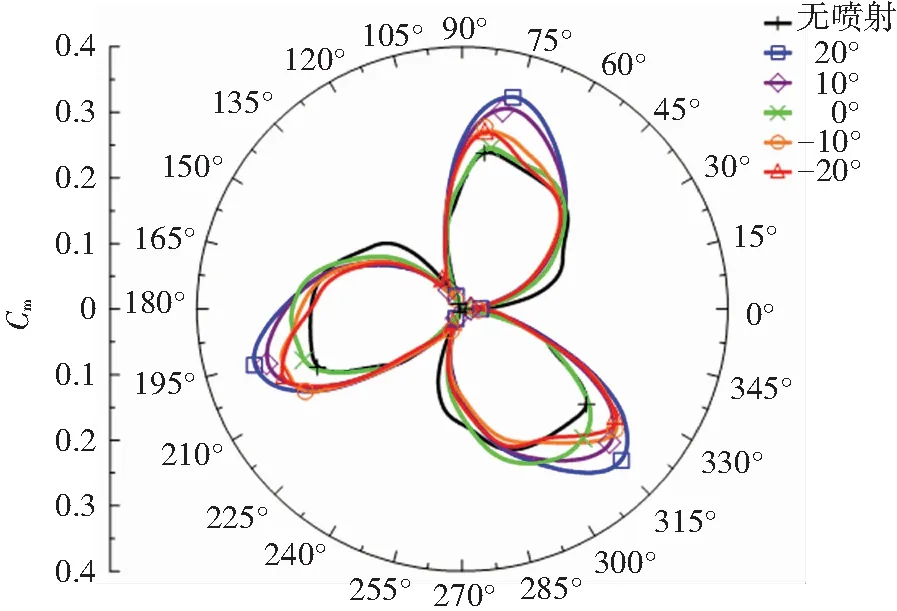
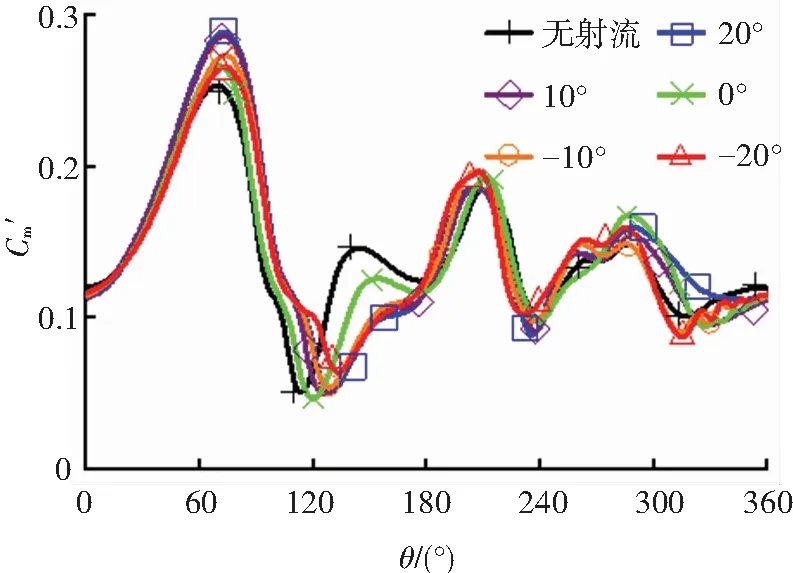
(a)λ=1.68

图11 不同方位角时单叶压力云图Fig.11 Single blade pressure contour of different azimuth angles

图12给出了λ=2.63时，0°与10°尾缘射流式垂直轴风力机叶片旋转一周内不同方位角的绕流场流动细节，并与无射流风力机进行对比分析。由图12可见，无射流风力机整机流场存在较大尺度的脱落涡，并且在多个相位角处都发生了旋涡从翼型吸力面直接产生并脱落的现象。由于垂直轴风力机动态尾迹效应，旋转过程中某一叶片会受到来自其他叶片尾流脱落涡或其他周期未耗散的尾涡干涉，这将导致流场中流动的非线性增强，气动载荷分布不均匀及转矩输出不稳定，进而使风力机气动性能、结构应力等受到严重影响。由图12还可观察到，0°与10°射流对风力机整机气动性能均有改善效果，但流场结构及旋涡运动也存在明显差异。10°射流可有效减弱翼型尾流脱落涡强度，缩小涡结构，削弱同一周期内尾流对下游翼型的干涉影响，并使上一周期翼型拖曳尾涡耗散更迅速，故整机涡斑区也明显减小，作用效果优于0°射流。通常叶片大范围流动分离会造成升阻比降低并致使风力机整体气动性能下降，此外还会导致非稳定的涡脱落，造成叶片受载更为复杂。合理角度的尾缘射流不仅会延缓流动分离，还会对动态尾迹效应产生良好的控制作用，使脱落涡与叶片撞击频率和强度减小，进而提高风力机的整机效率及运行稳定性。