松江有轨电车T1线轨下基础设计方案比选*
2022-12-13宋志慧秦晓光
宋志慧 秦晓光
(1. 山西电力职业技术学院建筑工程系, 030021, 太原;2. 上海市城市建设设计研究总院, 200011, 上海∥第一作者,高级工程师)
1 工程概况
松江有轨电车T1线位于长江三角洲堆积平原,地貌为湖沼平原Ⅰ-2区类型。该线路沿松江主要道路荣乐路贯穿松江老城。综合研究区域地质勘察资料以及室内试验数据得知,沿线地基土属于第四系地层。地基土主要由饱和黏性土、粉土及砂土组成,一般具有成层分布特点。地基土主要具有以下特征:① 呈流塑状态,压缩性高,承载力低;② 分布广泛,沉积厚度大;③ 潜水水位高。
本文应用有限元方法研究深厚软土地基有轨电车路基不均匀沉降问题,对有轨电车采用桩板结构、换填、复合地基等3种轨下基础设计方案进行了分析和比选。
2 桩板结构沉降计算
2.1 桩板结构方案介绍
针对铁路系统中桩板结构的特点,以及现代有轨电车荷载及其速度指标,提出了该有轨电车线路的轨下基础采用道床板-减沉疏桩一体化结构(以下简称“桩板结构”)方案。如图1所示,该桩板结构选用长度为21 m、φ400 mm的PHC(预应力高强度混凝土)管桩,施工作业面宽度为11 m。轨道采用短轨枕,轨枕埋入路基板中,并一次浇筑完成。
管线资料显示,埋深0.8~1.0 m的地下管线较多。桩板结构方案可减少大量管线的搬迁,且工期短、造价低、结构耐久性好,对周边管线的杂散电流腐蚀性较小。
桩板结构中每个结构单元长约20 m,单元之间设置变形缝。无砟轨道板与支撑板合二为一,采用钢筋混凝土结构承担有轨电车轮载。桩径为300~400 mm。每股道横向布置两根桩,桩间距沿线路纵向为5~7 m。桩顶设置横梁,中跨位置桩、横梁与支撑板浇筑成整体固结,边跨位置桩与横梁固结,两侧承载板搭接于梁顶。
2.2 地基固结引起的沉降计算
2.2.1 有限元模型的建立
为了较真实地得到路基施工期间沉降和工后沉降情况,利用有限元软件Plaxis 3D对这两部分沉降变形进行了模拟计算。路基土体模型采用实体单元,本构模型为理想弹塑性模型,屈服准则采用摩尔-库仑准则;钢筋混凝土板及横梁采用结构单元模拟,桩采用Embedded桩模拟。路基土层物理力学参数见表1。
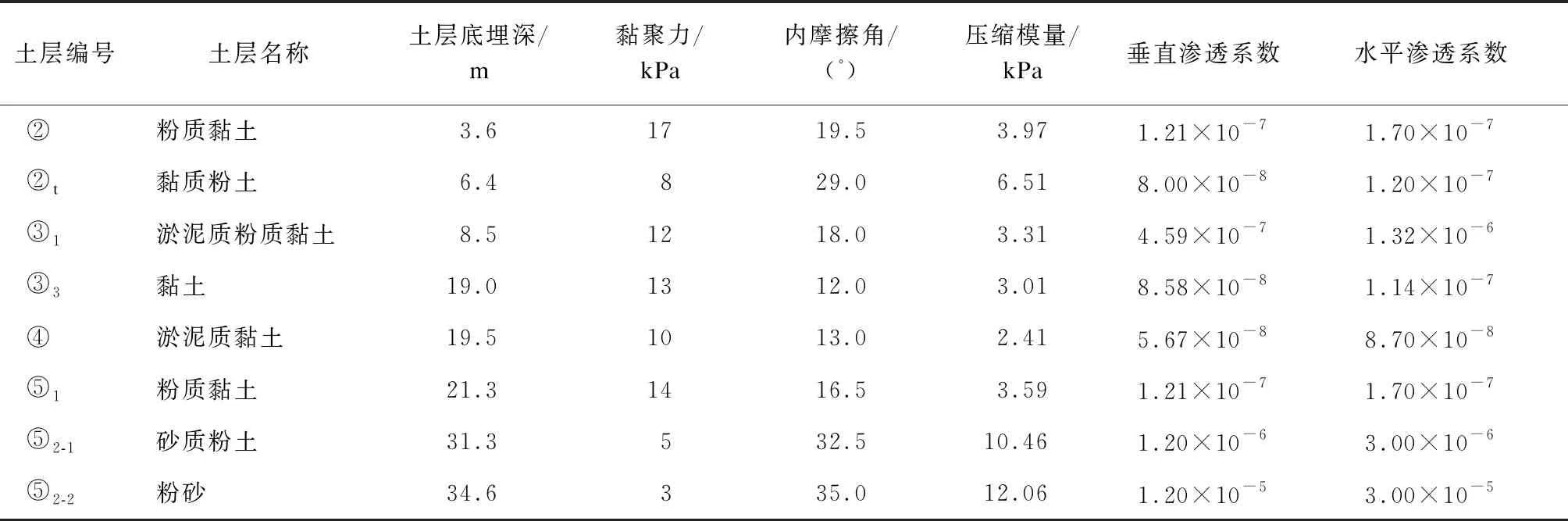
表1 路基土层物理力学参数
桩板结构沉降计算过程分为如下4个步骤[1]:① 土体自重应力的平衡计算;② 在模型中,激活管桩和承载板;③ 在模型中对有轨电车施加车辆荷载,计算该荷载作用下路基的瞬时沉降;④ 在车辆荷载作用下,对有轨电车路基固结沉降进行计算分析。
2.2.2 地基主固结沉降的分布规律
为研究路基土体固结引起的土层沉降,提取固结度达到95%时土体中超孔隙水压力的分布,如图2所示。由图2可知,持力层⑤2-1砂质粉土的渗透系数较大,因此土中的水压力全部消散;而其上部⑤1粉质黏土和④淤泥质黏土层的渗透系数较小,且桩板结构使桩周围土体中的超孔隙水压力并未完全消散,此时超孔隙水压力主要集中在④淤泥质黏土和⑤1粉质黏土层桩体周围。
根据路基固结沉降计算结果可知,路基固结沉降主要集中在上部粉土和黏土层,而下部砂层固结沉降接近于0。由于桩板结构将力通过桩向下传递,因此最大固结沉降发生于④淤泥质黏土层和⑤1粉质黏土层中,由固结引起的路基沉降为8.2 mm[2]。
本文分析时桩长取为21 m,桩底土层为砂土层。相关研究表明,无黏性土层的次固结绝对沉降一般不很大。而21 m深处的砂性土在自重应力和其他车辆、房屋荷载的作用下,已基本达到压密稳定状态,且有轨电车荷载并不大,因而对桩板结构的次固结沉降变形影响不大,可忽略不计。
2.3 有轨电车动荷载引起的沉降计算
2.3.1 土体动应力分布规律
采用ANSYS-DYNA软件建立车辆-轨道-路基三维耦合模型。建立模型时,车辆、转向架及轮对均采用刚体模拟,二系悬挂及扣件均采用弹簧阻尼单元模拟,钢轨采用梁单元模拟,轨下结构采用实体线弹性单元模拟[2]。
路基中土体竖向动应力分布如图2所示。由图2可见,有轨电车在动荷载作用下,土体竖向动应力在路基顶面达到最大,且其沿着深度增加逐渐递减,当深度在6 m以下时土体动应力则很小。因此,土体动应力仅需考虑埋深6 m以上区域。
桩板结构路基中土体动应力沿线路横向分布如3所示。由图3可见,桩板结构承担大部分土体动应力;当动应力传到路基中时,有轨电车荷载通过钢轨、桩板结构后其动应力已基本均匀;土体动应力集中现象出现在桩板结构边缘和路基的交界处,且此处竖向动应力最大;而两侧路基中土体动应力则呈迅速减小的趋势。
图4为板结构下表面路基中钢轨正下方两个点的竖向动应力时程曲线。由图5可见,当有轨电车通过时,车轮及转向架到达该点的正上方时,该点的竖向应力达到最大值;当车轮及转向架驶过后,该点的竖向应力迅速减小。
2.3.2 动荷载作用下的路基沉降量计算
对土体累积塑性应变沿着深度方向积分,得出路基的累积塑性变形S:
(1)
式中:
εp,i——第i层的累积塑性应变;
hi——第i层土体的厚度;
n——土体分层总数。
由于土层多为粉质黏土及淤泥质黏土,再加上埋深6 m之后路基的动应力及其变形较小,因此动应力引起的沉降仅需考虑埋深6 m范围内,即仅需考虑②粉质黏土和②t黏质粉土两层即可。根据上述粉质黏土和黏质粉土的物理性质勘查指标,利用累积塑形应变模型,可计算得到有轨电车动荷载作用100万次所引起的路基的沉降量为3.3 mm。
3 换填方案下路基沉降计算
3.1 换填方案介绍
根据有轨电车的轴重、轴距、运营速度进行分析,常规有轨电车可采用200 mm厚素混凝土支承层、400 mm厚水稳碎石表层和800 mm厚基床底层的换填路基,总开挖深度约为1.9 m。
3.2 路基沉降计算
3.2.1 路基固结沉降计算
3.2.1.1 主固结沉降计算
采用Plaxis 3D软件对路基施工期沉降和工后沉降进行模拟计算。土层参数见表1。根据地基固结沉降计算结果,得到最大固结沉降为52 mm,发生于地表轨道结构正下方。
3.2.1.2 次固结沉降计算
地基次固结沉降S0的计算公式为:
(2)
式中:
Ca,i——第i层土体的次固结系数;
e0,i——第i层土体的初始孔隙比;
t1——主固体时间;
t2——次固体时间。
结合松江有轨电车的实际情况及工程勘测资料,对土层次固结沉降值进行估算,见表2。
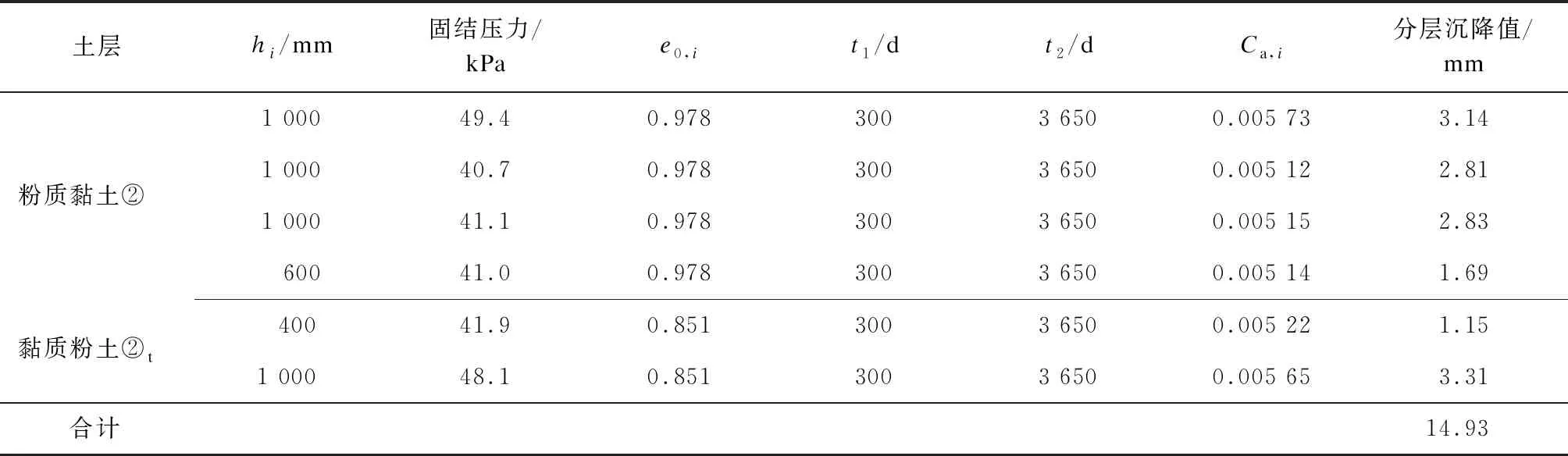
表2 换填方案下土体次固结分层沉降值估算
由表2可见,10年内路基土体次固结沉降约为15 mm。
3.2.2 有轨电车动荷载引起的路基沉降
图5为有轨电车动荷载引起的竖向动应力随深度分布曲线。由图5可见,土中竖向动应力在路基顶面最大,且沿着深度逐渐递减;当深度达到3 m以下时动应力水平很小,因此仅需考虑埋深3 m范围内土中动应力即可。基床表层动应力最大值达30~35 kPa左右。
图6为有轨电车动荷载引起的应力沿线路横向分布曲线。由图6可见,动应力在路基中的分布呈标准的马鞍形分布;在钢轨正下方,路基最大动应力达32 kPa;线路中心处路基动应力略有减小;而在轨道两侧向外,路基中动应力迅速衰减。
图7为有轨电车动荷载引起断面轨下某点竖向动应力时程曲线。由图7可见,有轨电车在轨道上运行,当车轮及转向架到达该点的正上方时,该点的竖向应力达到最大值;当车轮及转向架驶过后,该点的竖向应力迅速降低。
与桩板结构的计算方法相同,利用累积塑形应变模型,计算得到有轨电车动荷载作用100万次,引起的路基的沉降值为16 mm。
4 复合地基方案沉降计算
4.1 复合地基方案介绍
复合地基的加固原理是桩和桩间土共同直接承担荷载。本文复合地基方案中,选用φ0.5 m、桩间距为1.2 m、桩长为 21 m的三轴搅拌桩[3],在桩顶设置厚0.4 m左右的加筋垫层。
4.2 路基沉降计算
4.2.1 路基固结沉降计算
4.2.1.1 主固结沉降计算
采用Plaxis 3D软件对路基施工期沉降和工后沉降进行模拟计算。土层参数见表1。根据地基固结沉降计算结果,最大固结沉降为18 mm,发生于地表轨道结构正下方。
4.2.1.2 次固结沉降计算
据式(2)对土层次固结沉降值进行估算,见表3。
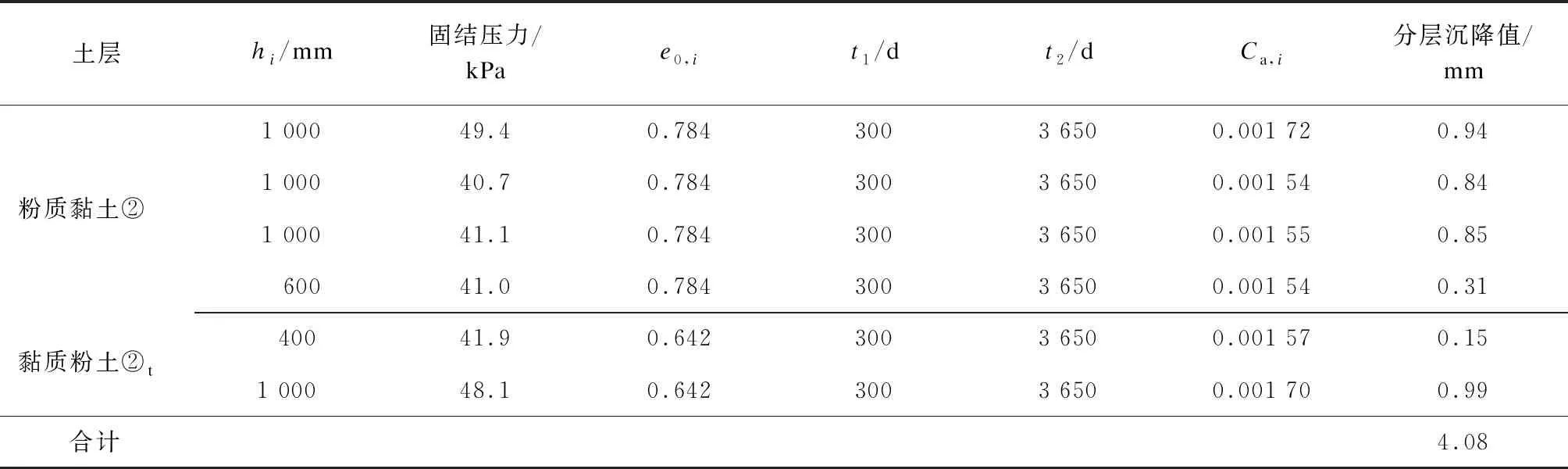
表3 复合地基方案下路基土体次固结分层沉降值估算
由表3可见,10年内路基土体次固结沉降值为4 mm。
4.2.2 有轨电车动荷载引起的路基沉降
图8为有轨电车动荷载引起的竖向动应力随深度分布曲线。由图8可见,土中竖向动应力在路基顶面最大,且沿着深度逐渐递减;当深度达到6 m以下时动应力水平很小,因此仅需考虑埋深6 m范围内土中动应力即可;埋深越浅处,路基土体的动应力越大,最大值达40~45 kPa左右。
图9为基床表面动应力沿线路横向分布曲线。由图9可见,土体动应力在路基中的分布呈标准的马鞍形分布;在轨道最下方,路基最大动应力达40 kPa;线路中心处路基动应力略有减小;而在轨道两侧向外,路基中动应力迅速衰减。
图10为路基左、右钢轨正下方两点的竖向动应力时程曲线。由图10可见,有轨电车在轨道上运行,当车轮及转向架到达该点的正上方时,该点的竖向应力达到最大值;当车轮及转向架驶过后,该点的应力迅速降低。
与换填方案计算方法相同,即仅需考虑埋深6 m范围内的②粉质黏土和②t黏质粉土两层即可。利用累积塑形应变模型,计算得到有轨电车动荷载作用100万次所引起路基的沉降值为8.9 mm。
5 考虑土层参数变异性引起的地基沉降
应用随机有限元,使各土层物理力学参数在地勘报告中的参数取值范围内随机变化,得到不同的地层参数组合形式,从而得出均质地层的最大和最小总沉降计算结果,如表4所示。由表4可见,由于均质地层物理力学参数在空间分布上的差异性,在有轨电车荷载作用下,桩板结构方案下有轨电车路基总沉降为10.1~13.3 mm,换填方案下有轨电车路基总沉降为67.6~97.4 mm,复合地基方案下有轨电车路基总沉降为25.8~35.1 mm。
6 结语
综上,与换填方案和复合地基方案相比,桩板结构方案的有轨电车路基总沉降值最小,为10.1~13.3 mm。此外,该方案在管线迁改、施工周期、后期维修养护和经济性等方面亦具有优势。经综合比选,推荐松江有轨电车路基处理采用桩板结构方案。

表4 各方案土层参数变异性引起的地基沉降值
