新一代信息技术产业中企业研发投入影响因素研究
2022-12-12张汝飞徐谢婷
张汝飞,徐谢婷,赵 彤
(1.河北地质大学 经济学院;2.自然资源资产资本研究中心,河北 石家庄 050031)
新一代信息技术产业是中国政府确立的战略性新兴产业之一,历经“十三五”期间的成长壮大,其规模和龙头企业数量已居各战略性新兴产业之首。“十四五”期间,中国政府更是指明新一代信息技术企业要持续向“数字产业化、产业数字化”方向取得新进步,加深传统行业数字化规模、优化经济结构、提高创新能力[1]。为了实现信息技术企业投资合理化、提升企业竞争力,本文通过二阶段变量选择方法,针对沪深两市181家信息技术类上市公司的386个财务相关指标,筛选出影响企业研发投入的重要因素。
近年来,在变量选择研究领域,Lasso、自适应Lasso(Adaptive Lasso,ALasso)、SCAD等惩罚回归模型是较为常用的方法。当特征维度大于样本量(即p>n),且在噪声变量与重要变量相关的情况下,这些方法会保留更多的噪声项,预测效果不尽理想[2]。因此,本文提出在高维普通最小二乘投影(Highdimensional Ordinary Least-squares Projection,HOLP)的基础上,结合自适应Lasso(ALasso)的组合二阶段模型以获得更小的均方误差(Mean Square Error,MSE),筛选出的变量用于描述企业研发投入更具代表性。
本文结构如下:(1)综述高维回归模型变量筛选方法的发展以及相关领域内的应用情况;(2)介绍HOLP-ALasso二阶段变量选择模型及估计步骤;(3)通 过 数 值 模 拟 比 较 基 于HOLP-Lasso、HOLP-ALasso、SIS-Lasso、FR-Lasso方 法 的 优 劣;(4)实证分析信息技术产业相关上市公司企业研发投入情况。
1 文献综述
在过去二十年中,国外有关高维数据的特征筛选方法已有大量研究成果,例如LASSO(Tibshirani,1996)[3],SCAD(Fan and Li,2001)[4],the Adaptive Lasso(Zou,2006)[5]等,但在变量个数p远大于样本量n时,上述方法在估计精度和计算效率上均难以得到保障。近年来,Fan等人(2008)提出确定独立筛选法(SIS),该方法第一阶段先对超高维数据进行降维,使得特征数降到样本量之下(p 相比国外学者,国内更侧重于应用层面。冯盼峰等(2018)研究基于随机森林两阶段逐步变量选择算法,第一阶段确定变量重要性排名,第二阶段进行逐步回归,实证显示该二阶段算法相比于SCAD、Elastic Net具有较高预测精度[9]。郭林等(2020)提出两阶段判别的信用评价指标组合方法,ROC曲线的有效性检验表明基于二阶段Logistic回归的判别模型预测概率高,能有效区分企业的违约损失率[10]。郭宇潇等(2021)提出一种排序和搜索策略的组合模型,将其结合不同机器学习方法,该模型筛选变量的准确度要优于偏最小二乘法-变量重要性投影(PLS-VIP)[11]。 综上所述,国外针对p远大于n的变量选择问题,是将特征维度快速降至样本量之下,再运用Lasso、SCAD等方法进行筛选;国内在变量选择方面的应用主要集中于机器学习领域,鲜有Lasso、ALasso、SCAD等方法与二阶段模型相比较的探索。因此,本文在Wang等人(2016)研究基础上,提出利用ALasso进行二层过滤变量,并通过比较HOLPLasso、HOLP-ALasso、SIS-Lasso、FR-Lasso的 预 测误差来评估组合模型的效果。 首先考虑线性回归模型: Y∈Rn是响应变量,X∈Rn是设计矩阵,ε∈Rn是独立同分布的误差项,εi~N(0,σ2)。 假定当p>n时,XXT可逆,XTX不可逆,引入Moore-Penrose广义逆处理Gram矩阵不可逆性。记全模型为M={x1,…,xp},真模型为MS,其中S={j:βj≠0,j=1,…,p}是基数为s=|S|的非零βj的指标集。为得到高维情况下筛选变量的方法,先给出β的一般线性估计类: A∈Rp×n把响应变量映射到估计值,在SIS中A=XT。 式(3)中Aε由零均值随机噪声项的线性组合组成,(AX)β是信号部分。在变量筛选的过程中要尽可能地保留信号变量部分,所以理想情况下的A将满足条件AX=I。如果满足上述情况,信号部分将会控制噪声部分。显然,当p 将变成普通的最小二乘估计。 但针对高维情况时,式(4)中的XTX是退化的,不满足AX是单位矩阵的条件。Wang等人(2016)提出使用X的某种广义逆:Moore-Penrose逆,令A=XT(XXT)-1。虽然在这种情况下AX不再是单位矩阵,但只要AX是对角占优矩阵,信号变量仍旧可以决定噪声变量。 定义高维普通最小二乘投影的估计量: 即 式(5)的第一项可以将估计量看成β的投影。 HOLP选择变量遵循的原则是对估计量β^进行排序并选择其中最大项。确切地说,令d为筛选后保留预测变量的数量,有子模型Md如下: 或者 Chen(2008)提出的改进BIC准则(Extended Bayesian Information Criteria,EBIC)或直接挑选个变量均可确定HOLP的筛选数目[12]。 最小化式(7)确定子模型中的变量个数d,其中p为特征维数 Zou(2006)针对Lasso估计存在有偏性且不满足Oracle性质而对L1惩罚项赋予了不同的权重,提出Adaptive Lasso,定义为: Zou(2006)指出用最优子集选择解决OLS估计解释能力弱的问题,但是模型不具有稳健性,微小的数据差异会引起较大偏差,降低预测精度;岭回归是一个连续的变量系数收缩过程,较为稳健,但是在拟合过程中没有系数被估计到0,达不到变量筛选的目的;Lasso存在变量选择不一致的情况,不具有Oracle性质,且估计是有偏的[5]。Adaptive Lasso解决上述模型中的问题,具有相合性及渐近正态性等性质,克服Lasso有偏估计的缺点,通过凸优化问题实现全局最优解。 HOLP的优点是具有确定筛选性质且计算过程高效,p>n情况下HOLP的计算复杂度为O(n2p)仅略次于SIS的计算复杂度O(np)[8];Wang等人(2016)发现HOLP的另一个优点是信号部分的尺度不变性,相比SIS可能会受缩放方式影响的缺点,HOLP更加稳定。在p>n时,HOLP中XXT矩阵总是满秩的,这表现出在相同情况下比OLS更优的变量选择。 Friedman(2010)提出沿正则化路径计算的坐标下降算法(Coordinate Descent),处理高维数据的同时还可以保留模型中的稀疏特征[13]。第二阶段基于Adaptive Lasso的凸优化问题保证用于求解Lasso的坐标下降算法可以同等效率地应用于Adaptive Lasso。具体步骤如下: (1)考虑第一阶段HOLP子模型中估计量个数d。 1Md为示性函数。使用EBIC准则对估计量进行排序,选择排序后的最大β^,剔除系数为0的不重要变量。 (2)应用基于坐标下降算法的Adaptive Lasso对β^进行二次处理。 惩罚参数λn由十折交叉验证(N=10)确定。λn=据此选择出系数不为0的变量为HOLP-ALasso最终筛选结果。 (3)评估不同二阶段模型的拟合效果。设第t次在训练集上的拟合值为,在预测集上的观测数据为yt,定义评价指标MSE,MSE越小,模型预测精度越高,特征筛选方法更优。 在此通过数值模拟评估HOLP-ALasso等二阶段模型预测效果,利用现有R包“glmnet”“screening”分析模拟数据筛选特征。本文参考Wang等人(2016)设置的模拟场景条件,结合实证研究的样本数据,综合确定所需样本量和特征维数[8]。 考虑线性模型: 其中x=(x1,…,xp)是预测变量,具体分布形式见下文讨论。样本量n=200,特征数p=500,随机误差ε~N(0,σε2)。根据信噪比SNR=Var(xTβ)/σε2,分别探讨SNR=50%和SNR=90%情况下计算得到的σε2,由模型形式生成响应变量y。具体而言,第一阶段比较HOLP,SIS和FR等模型选择正确模型的概率,已由Wang等人(2016)证明HOLP选择正确模型的概率总体上要优于SIS和FR,能更有效地进行特征筛选。本文重点对比Lasso和ALasso第二阶段模型拟合效果。考虑到特征之间的相关性对预测结果产生的影响,对自变量进行以下三种情况讨论并设定具体参数值: 场景1:自变量x=(x1,…,xp)独立同分布于标准正态分布N(0,1),令S={1,2,3,4,5},并将系数设定为: 场景2:自变量x=(x1,…,xp)服从多元正态分布N(0,Σ),协方差矩阵,其中ρ={0.4,0.6,0.8},将系数设定为: 场景3:自变量x1,…,x15构造形式如下: 其中k=0,1,2,3,4且Zi~N(0,1),控制组结构强度的参数δ2={0.1,0.05,0.01},x16,…,xp独立同分布于N(0,1),将系数设定为 以上三种场景各重复模拟T=100次,计算MSE判断二阶段变量选择方法的优劣。 当(n,p)=(200,500)时,表1展示了三种场景下的模型均方误差,第二阶段ALasso总体上比Lasso具有更低的均方误差,由于ALasso对Lasso系数的压缩程度进行了调整,使其具有Oracle性质且保持Lasso的凸性,从而模型预测精度高于Lasso。模拟实验表明ALasso的特征筛选效果优于Lasso,为探究二阶段组合模型的优劣,一并与其余四种方法进行比对。 表1 模型均方误差(MSE) 在SNR=50%的低信噪比情况下,基于二阶段HOLP-ALasso的组合方法均优于HOLP-Lasso、SIS-Lasso、FR-Lasso;HOLP-Lasso仅 次 于HOLPALasso,而SIS-Lasso效果最不理想。由此可以明显看到SIS的缺点,因SIS强烈依赖于重要特征与响应y之间有很强的边际相关性,但在高维数据中,预测变量之间往往存在相关性,这很有可能将与特征高度相关的不重要变量选入模型,这在场景2中很好地体现了这一点。 在SNR=90%的高信噪比情况下,尽管所有方法都有了显著提升,但HOLP-ALasso仍然保持整体的优良性。整体上来看,FR-Lasso与HOLPLasso效果相近,但在场景3中ρ=0.8时,FR-Lasso的表现优于HOLP-Lasso,这得益于FR能一步完成变量筛选,同时Wang(2009)证实了在高维环境下FR也能进行确定性筛选,但FR的计算成本显著高于其他方法,考虑到计算的简便性和效率,HOLP-ALasso仍然是效果最优的二阶段组合模型。 根据数值模拟结果,应用HOLP-ALasso实证筛选影响信息技术产业上市公司企业研发投入的关键因素。数据来自于国泰安数据库,包括2020年181家上市公司386个影响研发投入的财务指标,具体包括资产负债指标、利润指标以及现金流量指标等8个方面,如表2所示。 表2 影响研发投入的财务指标 将数据以7:3划分为训练集和测试集,分别用上述6种方法在训练集上拟合模型,并计算测试集上的均方误差,具体模型评估结果如表3所示。可以看出,基于二阶段HOLP-ALasso的均方误差最小,预测精度为0.110,模型拟合效果最优。 表3 模型评估结果 HOLP-ALasso最终从386个特征中筛选出9个变量,具体变量名见表4,其中有形资产带息债务比与研发投入呈负相关,其余9个变量与研发投入呈正相关。观察表4中的估计系数,管理费用、所有者权益和销售收入增加额较大程度地影响了研发投入金额,而其余6个变量虽然系数较小,但作为筛选出的重要变量也对结果产生了不可替代的作用。 表4 HOLP-ALasso法筛选的变量和估计系数 本文研究高维数据下不同二阶段模型的筛选效果,通过比较HOLP-Lasso、HOLP-ALasso、FRLasso等组合方法,证明HOLP-ALasso能有效选择变量并且具有较高的预测精度,最后将该方法应用于新一代信息技术产业中企业研发投入影响因素的分析。 在数值模拟中,本文提出的基于HOLP-ALasso模型从整体上看具有最小预测误差,相较于传统Lasso、ALasso和 二 阶 段HOLP-Lasso、SIS-Lasso、FR-Lasso,该方法能更有效的进行特征筛选。 此外,实证研究进一步验证了HOLP-ALasso能筛选出变量个数少且与响应变量较强相关的特征子集。最终筛选出的9个指标表明信息技术类上市公司的利润和盈利能力对企业研发投入产生较大的促进作用。企业在创新发展的道路上需要不断提高盈利能力,可以关注以下两个方面:一是紧跟市场需求,选择自身具有竞争力且拥有较好市场空间的发展方向;二是在企业成长过程中,及时对经营模式做出调整,以更好地适应市场需求的变动。2 模型建立
2.1 基本假设




2.2 高维普通最小二乘投影(HOLP)
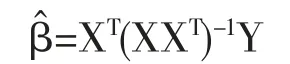



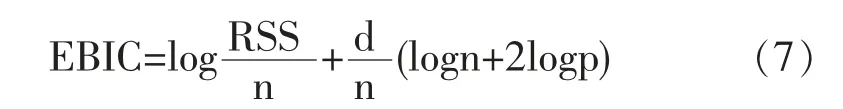
2.3 自适应LASSO(Adaptive Lasso)

2.4 算法求解
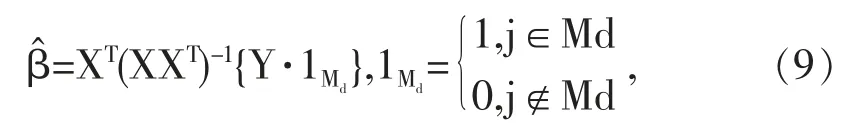
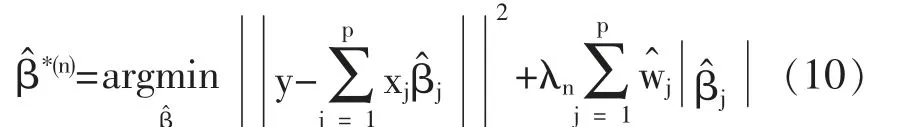
3 数值模拟
3.1 模拟参数设置

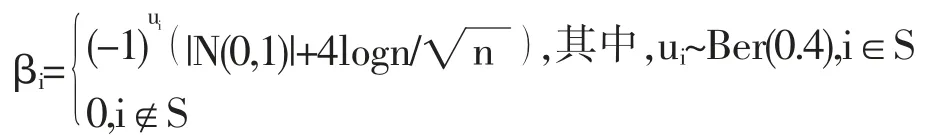
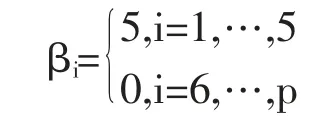

3.2 结果分析

4 实证研究
4.1 样本选取

4.2 结果分析
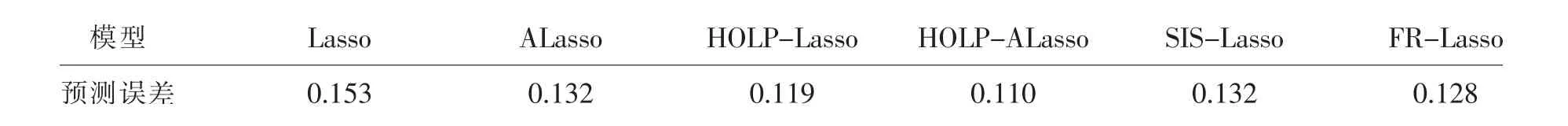

5 结论
