基于SVM步态分类的柔性外骨骼助力周期预测

赵朝勇，郭士杰，丁常松，陈强，孙磊

（1.河北工业大学省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2.河北省机器人感知与人机融合重点实验室，天津 300130；3.河北工业大学 机械工程学院，天津 300130；4.天津理工大学 电气电子工程学院，天津 300384）

0 引言

随着下肢外骨骼机器人的发展，其被广泛应用于医疗康复等领域。下肢助力外骨骼根据结构不同可分为刚性外骨骼和柔性外骨骼。刚性外骨骼提供较大的辅助扭矩，其缺点有关节中心与人体生物关节中心较难对齐、本身的惯性力大[1,2]、限制人体运动的自由度并影响穿戴的舒适性[3,4]。而柔性外骨骼相对刚性外骨骼使用柔性组织结构，具有灵活性高、惯性低、穿戴舒适等优点[5]。其在增强行走能力和补偿神经肌肉缺陷方面有明显的效果[6]。

柔性外骨骼通常根据助力函数生成期望辅助力的波形，助力周期参数（下文简称助力周期）影响助力波形的完整性[7]，现有的方法通过假定步态周期来提高步外骨骼的助力性能。哈佛大学Ding等[8～10]通过使用前两步的平均步幅作为下一步态的助力周期，并在此基础上调整辅助力参考轨迹，穿戴该装置行走的代谢成本较未穿戴情况下降低了17.4±3.2%。日本九州大学Jin等[11,12]采用过去五个步态助力周期的平均值作为下一步态的助力周期，实验结果显示能量消耗平均降低了约5.9%。中国科学院深圳先进技术研究院研制的助力髋关节外骨骼[13～15]，其生成期望力曲线的助力周期根据前一个步态的助力周期获得，平均净新陈代谢率降低了约17.45%。河北工业大学郭士杰等[16,17]团队提出一种新型助力函数，只需要调节辅助力幅值、助力周期、助力峰值偏移三个参数即可生成助力辅助函数，助力周期参数采用前一步的助力周期值作为下一步态助力函数的助力周期，经过实验验证使用该助力函数助力下的效果明显并且减小代谢量约11.2%。

尽管以上助力参数的研究已经取得了可喜的成果，但如何实时获得下一步态准确的助力周期鲜有研究。基于上述分析，提出了一种基于SVM（支持向量机）步态分类的外骨骼助力周期预测方法。解决了在变速运动状态下难以实时获得下一步态的助力周期的问题，并以此生成较为完整的助力轨迹，实现柔性外骨骼对助力周期的自适应。

1 搭建柔性外骨骼实验平台

为了解决上述自适应性问题，搭建了一台前拉式下肢柔性髋关节外骨骼（下文简称柔性外骨骼）。下位机将IMU（MPU 9250，采样频率200Hz）采集到的髋关节和质心加速度惯性信息，通过蓝牙模块（HC05）发送到上位机。上位机利用MATLAB（2020b）软件处理接收到的姿态信息，预测下一步的助力周期，并将实时预测的助力周期发回下位机。下位机实时更新助力周期参数，并由此生成助力轨迹控制电机转动。电机通过牵引和释放柔性卷带，实现对髋关节前屈动作的助力，结构如图1所示。

图1 柔性外骨骼样机

根据文献[17]选用助力辅助函数为：

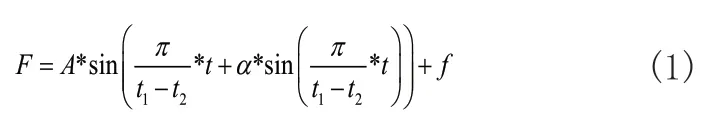
其中：

F为助力轨迹；

A为最大助力幅值，影响助力波形的峰值；

α影响助力波形峰值的偏移位置；f为预紧力，为提高控制器的响应能力，设置为3N；

T为助力周期（T=t1-t2），其影响助力波形的完整性，其中t1为助力结束时刻(未知参数)，是本文将要预测的重要参数；t2为助力起始时刻，为已知参数即髋关节伸展最大值对应时刻；

t为髋关节角度屈曲时间。

实时预测的助力周期为Td，Td小于T时外骨骼会提前结束助力。反之，外骨骼助力过程中会有力的突变，造成人体穿戴的不舒适性。为了提高外骨骼的自适应性以及舒适性，下文将对式(1)中助力周期T进行预测。

2 柔性外骨骼助力周期预测模型

2.1 基于SVM神经网络步态分类模型

在步态周期预测过程中，行走和跑步对于助力周期预测有很大的干扰性。为了能避免此类干扰，本文采取了基于Svm的步态识别算法，进行步态分类。利用其可以将低维非线性不可分转化为高维线性可分的特点[18]，能补充基于BP神经网络算法对大量样本的需求。

SVM算法利用内积核函数实现向高维空间的非线性映射，在高维空间构造步态分类超平面。针对步态非线性问题，采用径向基函数（RBF）映射得到的步态分类超平面可最大程度逼近样本空间，使得步态类型与步态分类超平面距离最大化，示意图如图2所示。所用的基函数表达式为：

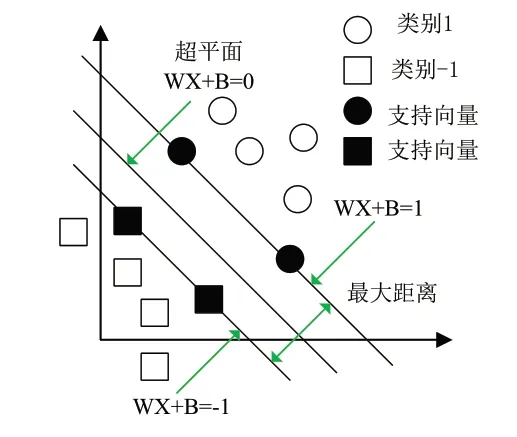
图2 最优超平面示意图

式(2)中||x1-x2||为两个样本点的距离，σ为核函数宽度。由此确定的超平面函数为：

式(3)中w为超平面法向量，φ(x)为输入步态特征向量x=(x1,x2,…,xn)由核函数K(x1,x2)映射到高维的新的特征向量，b为常数。

SVM步态分类问题转化为求步态类型的最大间隔问题，两类步态类型最大距离表达式为：

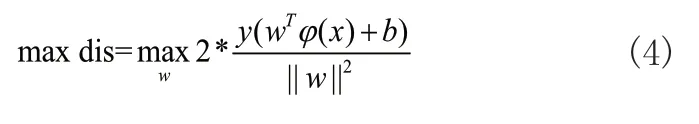
由于在步态分类面上满足：

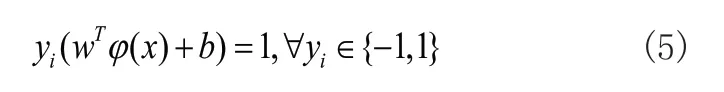
因此，SVM求解最优步态分类面的问题可归结为一个二次规划问题，如式(6)所示。为每个步态特征引入大于零的松弛变量ξi将不等式约束转化为等式约束如式(7)所示，根据拉格朗日乘子算法建立拉格朗日函数如式(8)所示。

式(8)中，λ，μ为拉格朗日乘子，C为惩罚因子，w，b，ξ为主要优化参数。

将式(8)两边分别对主要优化参数求导等于零并代回式(8)最终可得到最优步态分类超平面，其函数如式(9)所示：

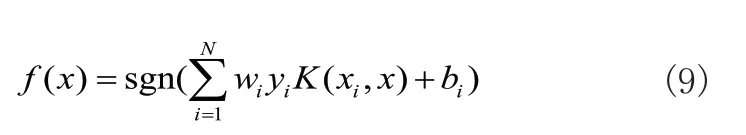
综上所述，SVM可应用于步态分类问题。选择二叉树结构的多分类方法训练SVM分类模型，最终可区分慢走、快走、小跑、上楼、下楼5种常规步态类型。

在SVM的输入特征选择方面，选择步态类型差异较大的特征如：下楼的髋关节角度曲线与其他步态差异较大[19]；跑步时脚着地时刻的加速度均小于零[20]；质心加速度标准差反映了加速度数据的离散程，人在静止时质心合加速度标准差几乎为零，而在运动时变化较大。由上述分析，可将髋关节角度信息和质心加速度作为SVM的输入特征向量。

采集髋关节摆动助力结束后1秒内的信息，根据重力加速度判断特征选取时刻，分类特征选取步骤如图3所示。

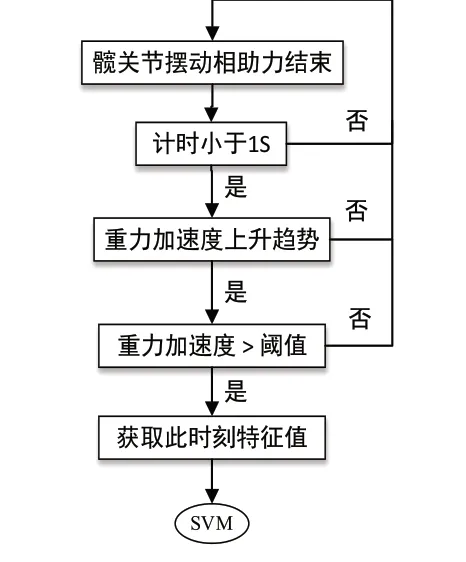
图3 步态类型特征选取流程图

图3中阈值通过实验获得取为1.2g(g=9.8m/s2)。

采集17名健康大学生慢走、快走、小跑上/下楼梯的数据，慢走步速约为4km/h，240步；快走步速约为6km/h，240步；小跑步速约为8km/h，240步；上下楼梯240节。

通过该SVM模型对测试集进行步态类型预测，得到五种步态类型的误检率和准确率如表1所示。

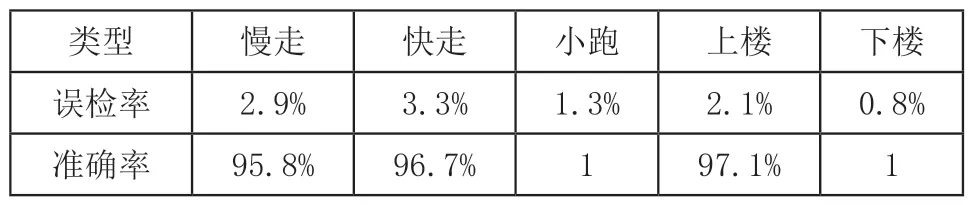
表1 基于SVM的外骨骼步态类型识别率

其中误检率是其他类型步态误认为是此步态类型的错误率，准确率为此步态正确判断为此步态。

实验表明SVM在步态分类上可以取得较高的识别率，可以排除助力周期预测的干扰性。

2.2 助力周期预测模型的建立

在SVM步态分类的基础上，建立针对变速行走步态下的助力周期预测模型(下文简称预测模型)。预测模型选择BP神经网络，其在理论和性能上都较为成熟，具有很强的非线性映射能力和泛化能力，是应用最广泛的神经网络之一[21]。

BP神经网络步态输入的特征对预测模型的精度有直接影响，尽可能将作用显著的自变量引入网络模型[22]。为此引入用以反映自变量与助力周期之间的相关密切程度统计指标[23](相关系数)，为BP神经网络输入的特征选择提供依据，相关系数计算公式如式(10)所示：

式(10)中，r为向量X与向量Y的相关系数，Cov(X,Y)为向量X与向量Y的协方差，Var[*]为向量*的方差。

预测模型的输入层为步态类型的特征向量，隐含层使用sigmod函数作为激活函数，提供非线性变化过程，其隐含层第i个神经元输出可表示为：

式(11)中wxi为输入层与隐含层之间的权值，xi为特征向量第i个特征，bi为输入层与输出层之间的权值。Purelin作为输出层线性激活函数，由公式(12)确定隐含节点数[24]。

式(12)中，[*]表示取整，m为隐含层的节点数；n为输入层节点数l为输出层节点数；c为1～10之间的整数。

预测模型的训练函数采用Trainbr算法避免产生过拟合。其效果评价指标采用均方跟误差（RMES）和决定系数（R2）。RMSE反映预测的助力周期与真的助力周期之间的偏差，其值越小表示预测效果越好，如式(13)所示；决定系数反映预测模型的回归拟合程度，其值越大拟合程度越好，预测性能也就越优，如式(14)所示。预测模型误差(error)计算公式如式(15)所示，准确率(accur)计算公式如式(16)所示：

其中：p为预测值,t为真实值，ā为真实值的均值，|*|表示取绝对值，N代表预测样本个数。

由上述分析可构建一个步态下的助力周期预测模型。将各种步态类型下的总体样本作为预测模型的样本空间，各种步态下的特征敏感性权重不同，由相关系数计算结果作为特征选择器来选择各步态的特征依据。

助力周期预测流程图如图4所示，整个预测模型共需10个svm步态分类模型和4个BP神经网络助力周期预测模型(对应慢走、快走、小跑、上楼梯)，下文将对此模型进行实验验证。

图4 助力周期预测流程图

2.3 助力周期预测模型的实验分析

选择17名健康大学生（身高：(170±5)cm，体重：(65±5)kg）穿戴柔性外骨骼采集慢走、快走、小跑、上下楼梯步态下的大腿部和后背处IMU惯性信息数据。走/跑的路线如图5中虚线箭头各2圈，上/下楼梯的路线为图5中6层教学楼，1层到6层4次往返。

图5 行走路线

采集步数如表2所示，取受试者各步态稳定的450步作为训练集，共3.825万个样本参与训练。

表2 每位受试者各步态下采集步数

由于在脚跟刚接触地时髋关节角度曲线会出现双波峰现象，为排除干扰，便于网络预测，对采集的髋关节角度、髋关节角速度进行0.5～2Hz的带通滤波。采集到的髋关节角度、髋关节角速度、重力加速度导入MATLAB的m文件，计算每个受试者髋关节伸展角度最大时刻的特征。

利用三层神经网络模型来构建预测模型，计算相关系数大于0.7的特征作为该步态类型下的模型输入特征。训练时采用均方根误差作为模型的损失函数，设置目标误差为10-3，学习率为10-2，训练次数为1000。根据特征选择器将各个步态下的特征输入相应BP神经网络预测模型，误差收敛速度如图6所示，以较快的速度收敛，迭代次数小于40次。

预测结果如图7所示，助力周期预测模型的预测准确率为97%，满足设计要求。需要指出的是下楼梯不参与助力周期预测训练，预测到下楼梯将切换至非助力的髋关节角度跟随模式。

图7中绿色线表示采用SVM进行步态分类的步态类型分界线，S1表示慢走，S2表示快走，S3表示小跑。

为验证模型的泛化能力需要对未参与训练的新受试者进行验证，为验证该方法对助力效果的影响，需要进行耗氧测试验证。

3 助力周期预测实验验证

3.1 实验

为了评估所设计预测模型的泛化能力，随机选择3名未参与模型训练的健康受试者(身高：(170±5)cm，体重：(65±5)kg)穿戴柔性外骨骼进行实验。受试者被要求沿图5路线以跑或走不恒定的速度各进行一圈，上1至6层楼梯一次，分别记录真实的助力周期和选用本文设计的助力周期预测模型计算模型预测助力周期的准确率。

为了评估所设计的外骨骼助力周期预测方法是否能为人体行走时为穿戴者提供有效助力，本文进行了另外一组实验。上述3名受试者穿戴柔性外骨骼，在室内跑步机上进行测试如图8所示。3名健康试验者被要求每次实验前需要测试受试者静息下5min内的呼吸代谢量，进行穿戴柔性外骨骼关电状态下4～8km/h的变步速行走5min，休息10min，穿戴柔性外骨骼工作状态下4～8km/h的变步速行走5min，用行走实验代谢量平均值减去静息阶段代谢量平均值以消除受试者随着时间累积的肌肉疲劳对每次实验初始状态的影响。通过耗氧装置(K4b2)进行耗氧代谢量测试，两组实验间隔1天，保证应试者体力充足。

3.2 实验结果分析

1）助力周期预测分析

3名受试者行走状态下助力周期预测结果如图9所示，准确率如表3所示。试验结果表明该助力周期预测模型可在变步速行走状态下可达到95.5%以上的准确率，比直接选用上一个步态的值作为下一步态助力的助力周期准确率提高了0.7%左右。如图9中对受试者A助力周期预测值局部放大，发现在速度变化较大时直接选用前一步的助力周期误差较，由于速度变化较大时采用前几步的助力周期平均值误差将更大，因此文中没有列出采用前几步的助力周期平均值。

表3 助力周期预测准确率 (%)

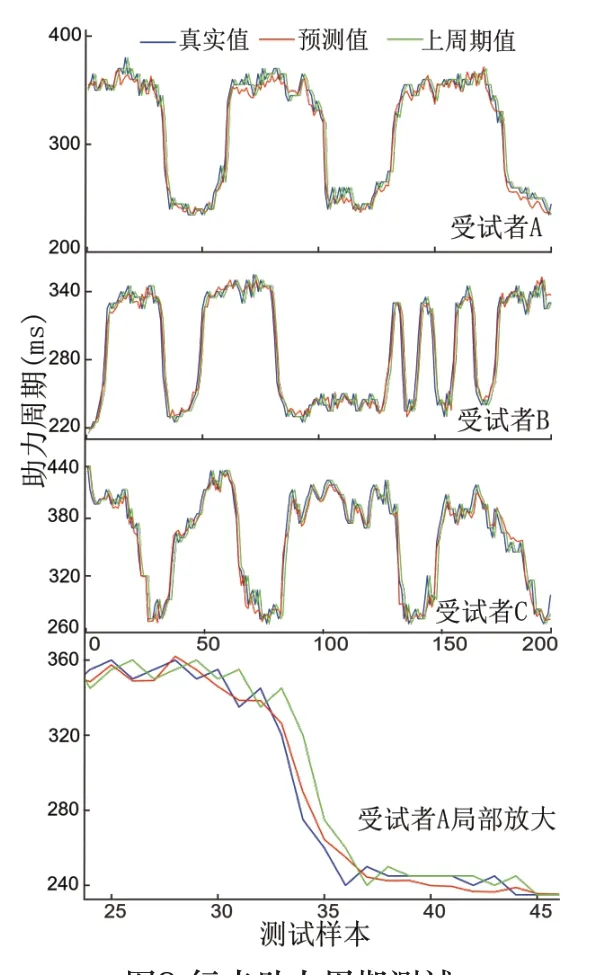
图9 行走助力周期测试

3名受试者上楼梯状态下助力周期预测结果如图 10所示。由于上楼梯行走速度相对变速行走较慢，相对变速行走状态下预测准确率有所下降，三名受试者助力周期预测准确率分别为90.439%、88.091%、90.104%，平均预测准确率为90.438%。

图10 上楼梯助力周期测试

2）耗氧量分析

对比预测助力周期参数后耗氧量的变化，可验证该助力周期预测的方法是否有助于降低代谢量，髋关节前屈助力对受试者耗氧量的影响如图11所示。相比穿戴外骨骼关机下行走，3名受试者在外骨骼采用该预测模型的辅助状态下行走净耗氧量分别减少了13.9927%、11.333%、13.769%，平均减少了13.031%，实验结果验证了该方法对助力效果的有效性。

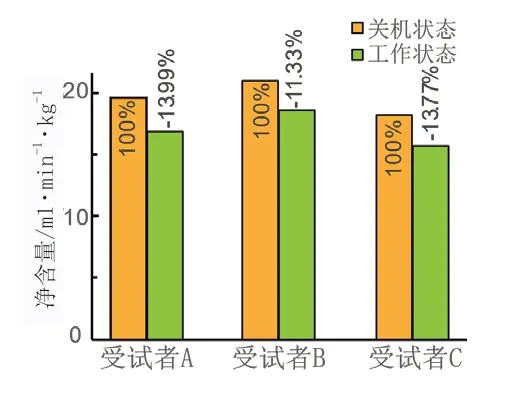
图11 耗氧代谢量测试对比

表3中，准确率1指助力周期预测模型预测结果相对真实助力周期的准确率；准确率2指直接选用上一个步态的助力周期值作为下一步态助力周期预测值相对真实助力周期的准确率。

4 结语

针对变速行走步态下柔性外骨骼难以实时预测下一步态助力周期参数的问题，在前人提出的柔性外骨骼助力函数基础上，提出了一种基于SVM+BP神经网络助力周期预测模型。该方法基于SVM算法模型对柔性外骨骼步态类型进行识别并针对不同的步态类型采用相应的BP神经网络预测模型预测下一步态下的助力周期。变速行走实验表明可以在变速行走情况下实时预测下一步态的助力周期并调整助力周期参数，预测准确率达到95.5%以上，通过耗氧验证了该方法对助力效果的有效性。穿戴外骨骼开电状态下采用预测助力周期相对比关电状态下耗氧量降低13.031%左右，实验结果表明在助力周期预测方面该方法能够使柔性外骨骼具有更好的自适应性，可满足柔性外骨骼助力系统在行走过程中的助力周期预测要求，为下肢外骨骼助力参数研究提供依据。

关于在更大的数据样本情况下，该方案的识别的准率有待进一步验证，在小于4Km/h的慢速行走状态下和上楼梯状态下该预测模型预测准确率有所降低，可结合其他传感器(如脑电)进行预判。今后工作的重点是优化网络模型和传感器配置，还需要进一步扩大不同人群的数据样本，确保方案的通用性和准确性。