基于高阻尼纳米复合材料的直角型黏弹性阻尼器的数值模拟

许俊红, 朱哲雨, 李爱群

(1. 南京林业大学 土木工程学院, 江苏 南京 210037; 2. 东南大学 土木工程学院, 江苏 南京 210096;3. 北京建筑大学 土木与交通工程学院, 北京 100044)

0 引言

梁柱节点是装配式钢结构中的重点部位,是极为薄弱的震害环节,其自身损伤形成塑性铰耗能的方式不仅容易造成节点破坏和结构整体倒塌,且在震后难以修复。因此,保证节点在地震中的良好性能尤为重要,这对于提高装配式钢结构建筑的抗震性能意义重大[1]。

近年来,国内外诸多学者基于被动控制思想,提出了在梁柱节点处设置阻尼器的方法来提高节点的抗震性能,并对节点转角阻尼器进行了理论试验和相关研究[2-3]。吴从晓等[4-5]、徐昕等[6-7]、朱琰洁等[8]、王艮平等[9-10]、Zhang等[11]和张恒[12]对扇形铅黏弹性或扇形黏弹性阻尼器进行了研究。考虑到节点处因变形过小无法充分发挥扇形黏弹性阻尼器的性能,李宏男等[13]提出了一种新型旋转放大式黏弹性阻尼器,可以通过放大节点处的位移使阻尼器产生较大变形,充分发挥了阻尼器的滞回性能。除了扇形铅黏弹性阻尼器,其他金属类型的节点阻尼器也受到了关注,如Yashar Bakhshayesh等[14]研究了一种放置在中心支撑钢结构框架节点处的新型钢阻尼器,其区别于普通钢阻尼器,具有剪切屈服机制,不仅经济且易于更换,可以耗散大部分地震能量。Soydan等[15]研究了一种在梁柱节点区域设置的铅挤压阻尼器,并进行了1/2缩尺比的不加固和加固结构模型的振动台试验和非线性动力时程仿真分析。Fathizadeh等[16]提出了一种新型弯曲钢阻尼器;Yang等[17]对一种放置在自复位钢筋混凝土基础和柱节点处的可更换阻尼器进行了研究;Piero Colajanni等[18]研究了一种布置在半预制混合钢桁架混凝土梁和现浇钢筋混凝土柱节点处的新型摩擦阻尼器,该阻尼器可以限制面板开裂,降低接头处剪切力的大小。

由以上研究可知,节点型阻尼器多以扇形阻尼器为主。但扇形阻尼器为一种异形结构[12],在制作过程中形状呈一定的弧形,制作构件的模具零件繁多[19],制作过程复杂。该特点成为扇形阻尼器加工过程中遇到的最大技术难点,这在一定程度上提高了阻尼器制作成本,制约了扇形阻尼器的推广应用。

鉴于此,为了能在有效保护结构节点的基础上进一步降低阻尼器的制作成本,并使节点阻尼器的制作简单化,本文提出了一种构造较为简单的直角型黏弹性阻尼器,其构造布置如图1所示。由图1可知,该阻尼器由螺栓连接于梁柱腋下,不仅具有体积小、不影响使用空间等优点,而且在安装装配式梁柱结构时还可以发挥固定框架梁的作用。该阻尼器的减震机理为:在地震水平作用下,节点处梁的弯曲变形引起框架梁柱节点的转动,使得分别连接于梁和柱的阻尼器钢板发生转动位移,从而带动直角型阻尼器材料层发生剪切变形,以达到耗能的目的。当阻尼器发生损伤时,虽然该部分功能会受到一定的影响甚至破坏,但结构整体损伤并不会过度发展,灾后可在合理的技术条件和经济条件下进行修复,恢复结构预期功能。

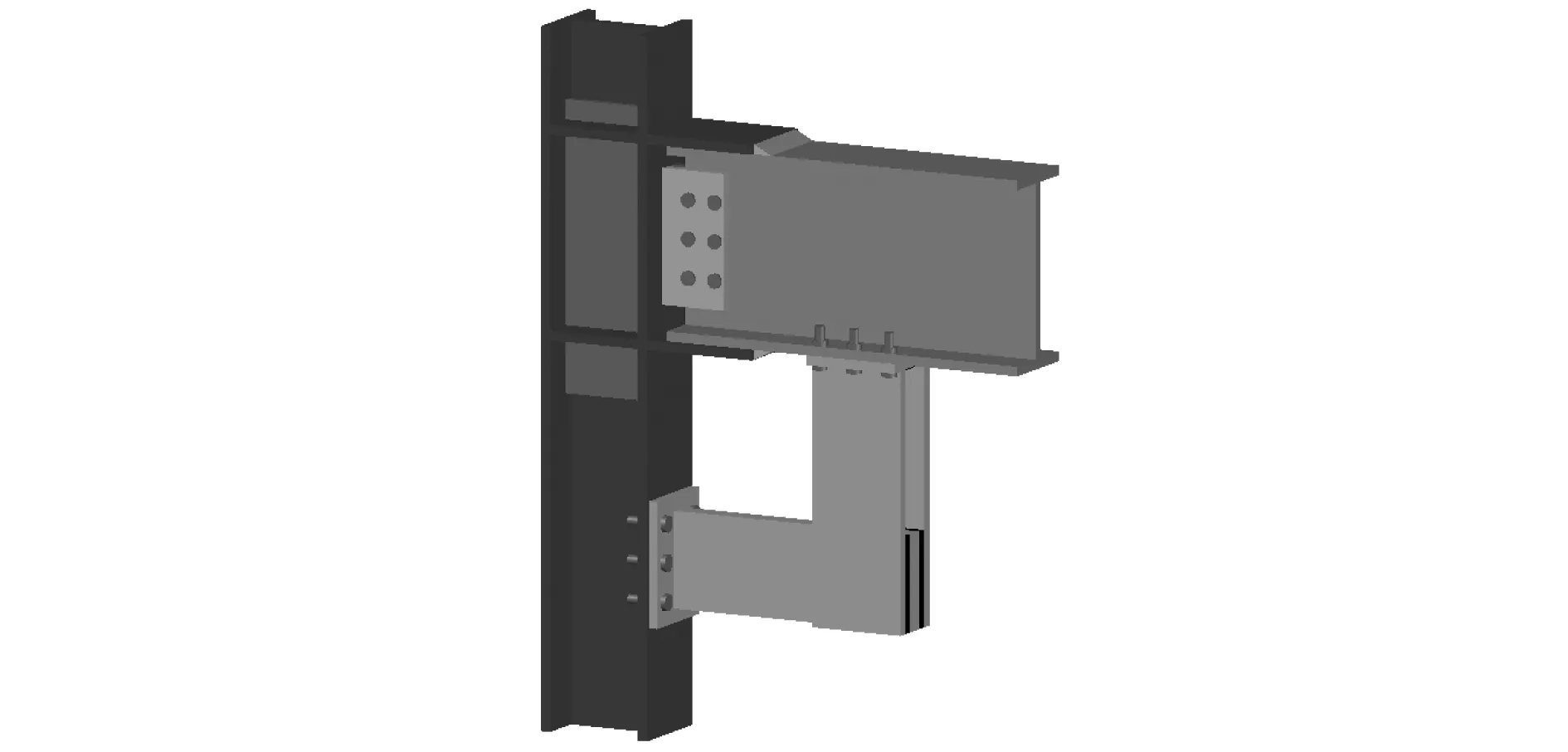
图1 梁柱节点处直角型黏弹性阻尼器布置图Fig.1 Layout of the right-angle viscoelastic damper at beam-column joints

作为高分子阻尼材料的典型代表,氟橡胶(Fluororubber,FKM)由于具有较高的氟氢比以及非常高的碳-氟键强度和饱和度(FKM分子结构式参看图2)[20],从而具有优异的热稳定性、耐腐蚀性和耐油性等特质。这些性能使得FKM广泛应用于高铁快轨、航空航天发动机、汽车工业、建筑结构等诸多领域[21-22]。使用填料对FKM进行改性不仅可以增大其体积,同时可以有效改善FKM的力学性能以及加工工艺性能,并降低使用成本。Righetti等[23]研究了炭黑填料浓度对溶胀交联和含氟弹性体橡胶的玻璃化转变温度的影响。Kader等[24]研究了硫化填料对FKM和丙烯酸橡胶-氟橡胶共混物硫化、机械、老化和溶胀性能的影响。目前对于FKM的改性材料多以石墨、碳纤维、碳化硼等为主,而将高岭土经过一系列的工艺制备成纳米偏高岭土(Nano-metakaolin,NMK),以此作为FKM的补强填料,具有白度高、粒度细、分散性好以及高分子化合物相容性好等特点[25]。同时,NMK是纳米级材料,在提供弱的阳离子交换性和强离子吸附性方面有独特优势,且方便易得、成本低廉,因此具有较广泛的应用价值、推广价值和现实工程意义。

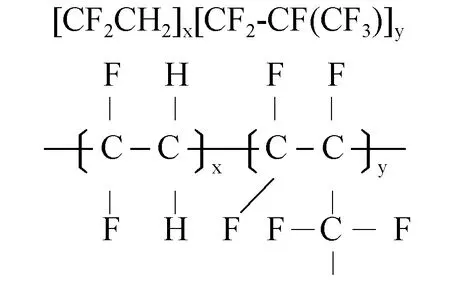
图2 26型氟橡胶分子结构式Fig.2 Molecular structure of type 26 fluoroelastomer

因此,本文首先制备高阻尼性能的纳米偏高岭土/氟橡胶(NMK/FKM)复合材料,并对该新型材料进行动态力学性能试验和静态力学试验;其次,以NMK/FKM纳米复合材料为核心耗能材料,对本文提出的直角型黏弹性阻尼器进行ABAQUS有限元模拟研究,得出直角型阻尼器力学性能参数的位移相关性、频率相关性以及黏弹性材料层和约束钢板的应力分布;最后探讨黏弹性材料层厚度和阻尼器高跨比对其滞回性能的影响。

1 宽阻尼温域NMK/FKM复合材料的制作与性能表征

1.1 NMK/FKM复合材料的制备

选用FKM基体胶,将其在室温下塑炼3遍,然后包辊、打三角包、出片,以此制得FKM。硫化条件如下:首先,分别选用AF和BPP作为硫化剂和促进剂;然后按质量比20/100计算称取相应质量的NMK(内蒙古超牌偏高岭土有限公司生产),和FKM进行共混,并于平板硫化机上硫化制备NMK/FKM纳米复合材料。其中,硫化参数包括:一段硫化(160 ℃下16 min,压力10 MPa)和二段硫化(180 ℃下6 h)。

1.2 NMK/FKM复合材料的动态力学热分析

动态力学性能表征采用德国NETZSCH公司生产的DMA 242E型动态热机械分析仪(图3)进行测试。试样剪裁成尺寸为50 mm(长)×9 mm(宽)×4.9 mm(高)的柱体。试验加载条件为:振幅10 μm;测试频率分别为0.5、1.0、1.5、2.0 Hz;温度扫描范围为-40～60 ℃;升温速率为5 ℃/min。

图3 DMA 242E型动态热机械分析仪Fig.3 DMA 242E dynamic thermomechanical analyzer

图4显示了复合材料在0.5、1.0、1.5、2.0 Hz工况下的损耗模量(E″)、存储模量(E′)和损耗因子(tanδ)随温度的变化曲线。由图4可知,NMK/FKM纳米复合材料在0.5、1.0、1.5、2.0 Hz工况下的阻尼性能发挥稳定,其宽阻尼温域(即损耗因子tanδ大于0.5的温度区间)随频率的增大呈先增大后减小的趋势,分别为23 ℃、56 ℃、60 ℃、30 ℃,在频率为1.5 Hz时达到峰值(60 ℃),即图4(c)中红色虚线所示横坐标范围。随着频率的增大,玻璃态转变峰温度(损耗因子达到峰值时所处的温度)由低温向高温处移动,存储模量峰值和损耗模量峰值亦表现出与宽阻尼温域相近的变化趋势,同样，二者的峰值均出现在1.5 Hz工况下。

图4 NMK/FKM纳米复合材料的E″-T、E′-T、tanδ-T曲线Fig.4 E″-T、E′-T,tanδ-T curves of NMK/FKM nanocomposite

表征材料阻尼性能更科学的一种方法是将聚合物损耗因子对温度的积分面积tanδArea(TA值)作为阻尼评价的指标。表1给出了NMK/FKM复合材料在不同频率下的TA值,即损耗因子-温度曲线(tanδ-T)下包裹的面积。由表1可知,复合材料的TA值在1.5 Hz时达到峰值14.2。综合材料在4种频率下宽阻尼温域的变化特征(图4)可知,该材料在1.5 Hz时阻尼性能最佳,其他频率工况下的阻尼性能与1.5 Hz工况下相差不大,皆有较好的耗能特性。

表1 NMK/FKM纳米复合材料的TA值

1.3 NMK/FKM复合材料的静态力学试验

为了验证和拟合数值模型,对NMK/FKM复合材料进行了一系列静态力学试验,试验过程如图5所示,图中红线圆圈部分为正在拉伸中的哑铃状试样。试验结果显示,复合材料的拉伸强度、扯断伸长率和扯断永久变形分别为16 MPa、382%和21%,满足建筑消能阻尼器规范的要求。将该试验结果用于下一节的ABAQUS建模当中。

图5 NMK/FKM纳米复合材料拉伸试验Fig.5 Tensile test of NMK/FKM nanocomposite

2 直角型黏弹性阻尼器设计

本文所提出的直角型黏弹性阻尼器包含三层钢板和两层黏弹性材料,其两侧剪切钢板与中间约束钢板呈90°夹角,构造形式如图6所示。其中,中间钢板厚度为20 mm,两侧黏弹性材料层厚度为10 mm,最外侧约束钢板厚度为12 mm。黏弹性材料层的规格为100 mm(长)×100 mm(宽),剪切钢板和约束钢板的截面尺寸均为270 mm(长) × 100 mm(宽)。为实现装配式钢结构快速施工的目的,阻尼器和梁柱结构之间采用螺栓连接,一则螺栓连接可以便于阻尼器的更换,二则螺栓连接的抗震性能要优于焊接[26]。

图6 直角型黏弹性阻尼装置结构尺寸图(单位:mm)Fig.6 Structural dimension of the right-angle viscoelastic damping device (Unit :mm)

3 直角型黏弹性阻尼器有限元模型的建立

3.1 有限元模型建立和单元类型选取

采用ABAQUS有限元软件对直角型黏弹性阻尼器进行模拟分析。在实际工程中,黏弹性材料与钢板之间是通过硫化等措施结合形成整体的,在使用过程中阻尼器各层结合也十分紧密。所以在建模中,黏弹性层与钢板之间通过Tie绑定的方式连接。对于钢板材料,采用C3D8R网格单元类型进行模拟,黏弹性材料则采用C3D8H网格单元类型进行模拟。

3.2 材料定义、边界条件和加载工况

约束钢板与剪切钢板均采用Q235钢,材料模型假定为线弹性材料,弹性模量取2.06×105MPa,泊松比为0.3。

在本次模拟中,对于黏弹性材料共赋予3种定义:质量密度、超弹性和黏弹性。质量密度为1.5 g·cm-3,超弹性和黏弹性参数则由1.3节中的试验结果拟合得出。超弹性属性参数采用各向同性,且每单位体积的应变能函数取Mooney-Rivlin模型(应变势能阶次为1)进行模拟，拟合得到的橡胶超弹性本构模型的具体参数如表2所列。表中,C10、C01为材料剪切性能参数;D1为材料压缩性能参数。

表2 NMK/FKM纳米复合材料的超弹性参数

黏弹性属性参数采用Prony序列来表达橡胶材料对时间的依赖特性,拟合得到的橡胶黏弹性松弛系数如表3所列。表中,gi和ki为对应的无量纲模量;τi为松弛时间。本次计算采用动力隐式分析步。

表3 NMK/FKM纳米复合材料的黏弹性参数Table 3 Viscoelastic parameters of NMK/FKM nanocomposite

模拟中,根据图1中直角型阻尼器的实际运动方向,加载模式为:在约束钢板的一端,采用固结的方式进行固定;对于剪切钢板的一端,在其顶端耦合一点,通过在耦合点施加正弦位移荷载模拟往返剪切运动,并约束除剪切方向之外的位移。在数值模拟中,考虑到与1.2节NMK/FKM纳米复合材料温度扫描试验的频率设置一致,对阻尼器的工况设计亦考虑4种频率工况,分别为0.5 Hz、1.0 Hz、1.5 Hz和2.0 Hz,且每种频率下包含2 mm、5 mm、10 mm、20 mm、30 mm和50 mm 5种位移幅值,共有24种加载工况,以深入考察阻尼器的位移相关性和频率相关性。数值模拟中设定破坏条件为:当阻尼层发生60 mm剪切应变时,钢板与阻尼材料撕裂,阻尼器破坏。

4 有限元结果分析

4.1 滞回曲线

基于上述建模方法,对阻尼器模拟结果与试验结果进行对比,图7所示为采用本文建模方法与试验所得滞回曲线的对比图。由图可知,二者吻合较为理想,上述的有限元建模方法可应用于直角型黏弹性阻尼器的有限元模拟分析。

图7 直角型阻尼器试验与模拟滞回曲线对比图Fig.7 Comparison diagram of experimental and simulated hysteretic curves of the right-angle damper

图8为加载频率分别为0.5、1.0、1.5和2.0 Hz,位移幅值分别为2、5、10、20、30和50 mm时,直角型黏弹性阻尼器的滞回曲线。由图8可以看出,滞回环形状良好,较为饱满。在频率相关性方面,滞回环斜率随频率的增大而增大,表现出频率越高刚度越大的动力特性。在不同频率作用下,随着位移幅值的增大,滞回环的面积均逐渐增大。当加载频率为0.5 Hz时,滞回环的斜率不随位移幅值的增加而增大;当频率大于0.5 Hz时,滞回环的斜率则随着位移幅值的增大而增大。可见直角型黏弹性阻尼器的动力特性表现为位移幅值越大,其刚度也越大。从图8可知,在0.5、1.0和1.5 Hz工况下,滞回环形状随着位移幅值的增大发生了不同变化,直角型阻尼器的滞回特性表现为非线性类型;当频率升至2.0 Hz时,滞回环形状则不随位移幅值的变化而变化,此时阻尼器的滞回特性为线性。需注意的是,非线性和线性两种类型下,对于等效刚度和等效阻尼比的计算是不同的。

图8 直角型黏弹性阻尼器在不同频率和不同位移幅值下的滞回曲线Fig.8 Hysteretic curves of the right-angle viscoelastic damper under different frequencies and different displacement amplitudes

4.2 骨架曲线

骨架曲线为往复荷载作用下所得各个滞回环的最大荷载点依次连接而成的曲线,直角型黏弹性阻尼器各频率下的骨架曲线如图9所示。由图9可知,模拟的最大荷载在正向加载和反向加载时相差较小,各频率下的骨架曲线大致呈中心对称。在不同位移加载下,阻尼器的刚度未发生下降现象;所有工况下的最大荷载为85 kN左右,阻尼器刚度并未发生很大变化,所以阻尼器在整个工作中状态良好。当阻尼器变形达到极限位移时,荷载仍未出现下降段,说明直角型阻尼器具有良好的变形和耗能能力。

图9 直角型黏弹性阻尼器在不同频率下的骨架曲线Fig.9 Skeleton curves of the right-angle viscoelastic damper at different frequencies

4.3 黏弹性材料层应力分布

为了研究直角型黏弹性阻尼器黏弹性材料层的应力分布,取1.0 Hz频率时不同位移幅值工况进行研究,结果如图10所示。由图10可知,在各位移幅值下,两块黏弹性材料层的应力分布基本对称,且随着位移幅值的增大各处的应力也增大。应力的极值点均出现在与中间钢板连接处的边缘,且在材料层中心点处出现应力变化。从变形来看,当位移幅值为50 mm时,黏弹性材料层发生了较大变形。

图10 频率1.0 Hz、不同位移幅值工况下黏弹性材料层应力图(单位:MPa)Fig.10 Stress diagram of viscoelastic material layers under a frequency of 1.0 Hz and different displacement amplitudes (Unit :MPa)

4.4 约束钢板应力分布

不同于常规黏弹性阻尼器,直角型阻尼器的约束钢板和中间钢板呈垂直构造,这可能会对阻尼器的耗能特性产生较大影响,因此有必要对钢板的应力分布进行研究。图11为频率为1.0 Hz时,不同位移幅值工况下约束钢板的应力分布图。由图11可以看出,钢板应力随着位移幅值的增大而增大。

图11 频率1.0 Hz、不同位移幅值工况下的钢板应力图 (单位:MPa)Fig.11 Stress diagram of steel plates under a frequency of 1.0 Hz and different displacement amplitudes (Unit :MPa)

对比图10可知,相对于黏弹性材料层的应力,钢板应力要大得多。所有位移幅值工况下,钢板应力的极值点皆出现在钢板固定端的角点处,且应力对称分布,从钢板固定端向另一端呈发散式分布。

5 力学性能指标分析

5.1 最大阻尼力

最大阻尼力是阻尼器在整个往复剪切过程中构件所承受的最大荷载,图12为直角型黏弹性阻尼器的最大阻尼力相关性分析图。由图12(a)可以得出,当位移幅值为50 mm且频率为2.0 Hz时,出现所有工况下的最大阻尼力(88.9 kN);4种频率下的最大阻尼力都呈现随位移幅值的增大而单调递增的趋势,且每种频率下增加的幅度相似。由图12(b)可知,在同一位移幅值下,随着频率的增大最大阻尼力也略有增大;当位移幅值达到20 mm及以上时,最大阻尼力随频率增加的幅度变大。

图12 最大阻尼力相关性分析图Fig.12 Correlation analysis of the maximum damping force

5.2 存储刚度

存储刚度为阻尼器最大位移时的荷载与最大位移的比值,表征了阻尼器构件在能量转换方面的性能,图13为直角型黏弹性阻尼器的存储刚度相关性分析图。从图13(a)可知,每种频率工况下构件的存储刚度随位移的增大呈单调递增的趋;各频率工况都在50 mm位移幅值时达到最大存储刚度,且2.0 Hz时存储刚度达到所有工况下的最大值1.78 kN/mm。由图13(b)可知,所有位移幅值下存储刚度都随频率的增大而单调递增,与位移相关性规律相似。

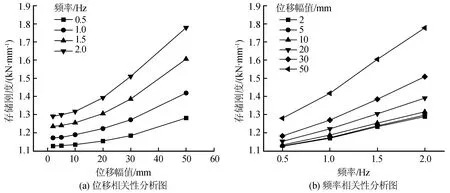
图13 存储刚度相关性分析图Fig.13 Correlation analysis of the storage stiffness

5.3 损耗刚度

损耗刚度是阻尼器零位移时的荷载与最大位移的比值,是反映阻尼器构件在能量损耗方面的能力指标,图14为直角型黏弹性阻尼器的损耗刚度相关性分析图。从图14(a)可知,当位移幅值小于20 mm时,各频率下阻尼器的损耗刚度无明显变化;位移幅值大于20 mm后,各频率下损耗刚度随着位移的增大也逐渐增大。频率为1.5 Hz时损耗刚度的曲线变化与其他三种频率工况有所区别,损耗刚度一直呈增长趋势。损耗刚度最大值出现在频率1.5 Hz且位移幅值50 mm的工况下,为0.896 kN/mm。从图14(b)可知,各种位移幅值下,损耗刚度随频率的增大呈现先增大后减小的趋势。

图14 损耗刚度相关性分析图Fig.14 Correlation analysis of the loss stiffness

5.4 等效阻尼系数

等效阻尼系数为阻尼器损耗刚度与加载频率的比值,图15为直角型黏弹性阻尼器的等效阻尼系数相关性分析图。由图15(a)可得,在位移相关性方面,当频率为1.5 Hz时，阻尼器等效阻尼系数随位移幅值的增大而增大；其他加载频率下，等效阻尼系数则随位移幅值的增大呈先减后增的趋势。由图15(b)可知，位移幅值大于10 mm后，等效阻尼系数呈开口向下抛物线型变化。在所有工况中,等效阻尼系数在1.5 Hz频率和50 mm位移幅值下出现最大值0.597 kN·s/mm。

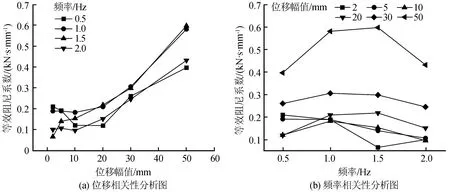
图15 等效阻尼系数相关性分析图Fig.15 Correlation analysis of the equivalent damping coefficient

5.5 损耗因子

损耗因子为阻尼器损耗刚度与存储刚度的比值,图16为直角型黏弹性阻尼器的损耗因子相关性分析图。由图16可得,阻尼器损耗因子的位移相关性与频率相关性的变化趋势与损耗刚度类似;当频率为1.5 Hz且位移幅值为50 mm时,损耗因子达到峰值0.56,5.4节中等效阻尼系数也在该工况下出现最大值。这与1.2节给出的结论“当频率为1.5 Hz时,阻尼材料的宽阻尼温域和TA值皆达到峰值,该工况下材料的阻尼性能最佳”,保持了一定程度上的一致性。该结论也从侧面验证了数值模型的有效性。

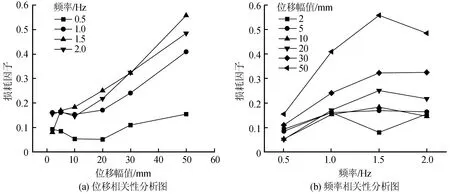
图16 损耗因子相关性分析图Fig.16 Correlation analysis of the loss factor

6 其他相关性分析

6.1 黏弹性材料层厚度相关性分析

为了更全面地探究直角型黏弹性阻尼器的性能,本研究考虑了黏弹性材料层厚度对阻尼器滞回性能的影响,在上述结构尺寸和形状的基础上,通过改变黏弹性材料层厚度对阻尼器进行研究。厚度分别取6 mm、10 mm、15 mm和20 mm,加载位移幅值与加载频率分别取10 mm和1.0 Hz,计算得出各工况下的滞回曲线如图17所示。由图17可知,随着黏弹性材料层厚度的增大,滞回曲线的面积逐渐减小,最大阻尼力也逐渐减小;随着厚度的增加,滞回环的斜率减小,说明阻尼器的刚度也在逐渐变小。

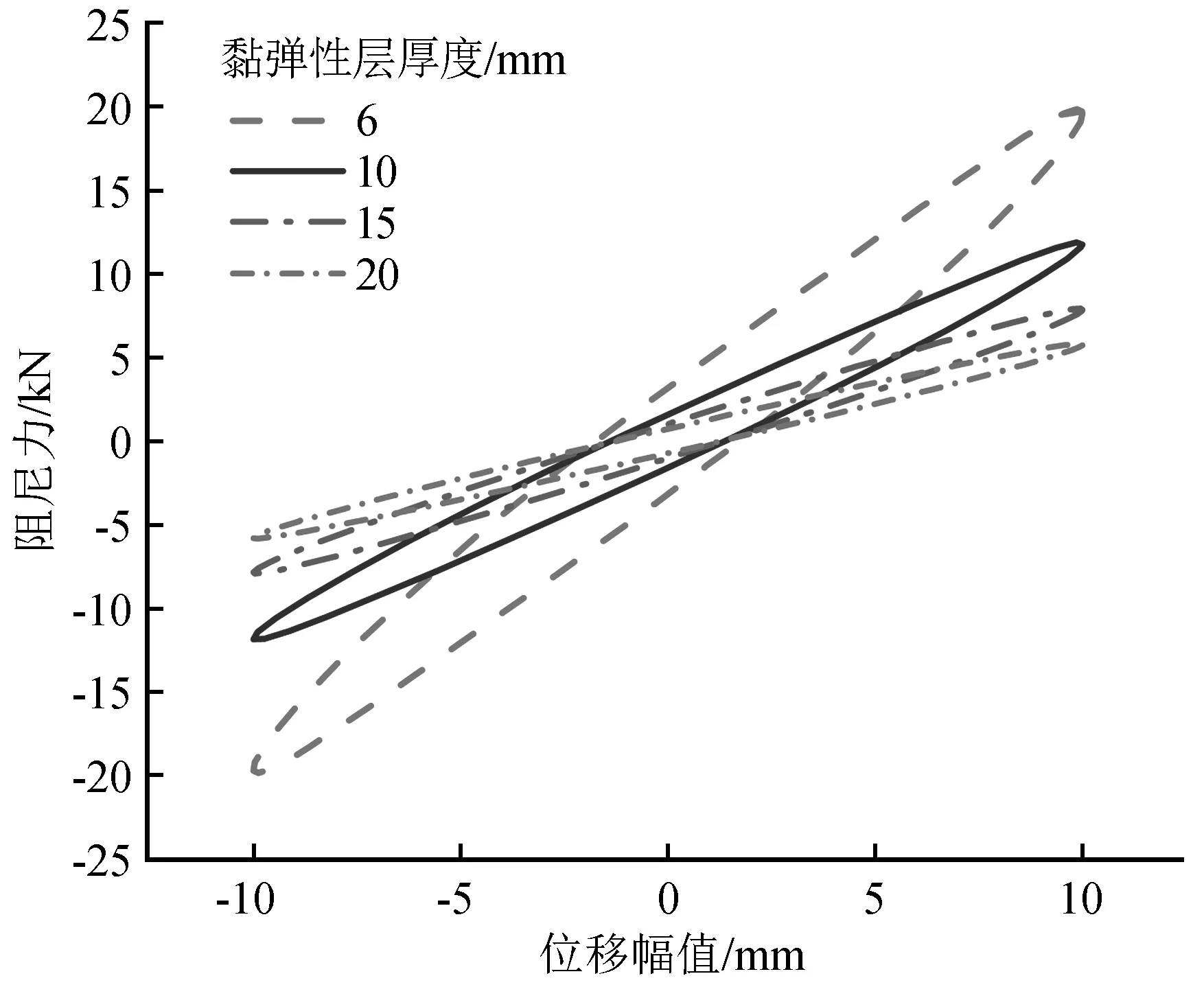
图17 黏弹性材料层厚度相关性分析Fig.17 Correlation analysis of viscoelastic material layers

从这一点来看,黏弹性材料层不宜设计过厚,以免对阻尼器的耗能性能产生不利影响。通过研究得出,当黏弹性材料层的规格为100 mm(长)×100 mm(宽)时,材料层最佳厚度为6 mm。在进行阻尼器设计的时候,宜通过有限元分析对最佳材料厚度进行计算验证,从而发挥阻尼器的最大效能。

6.2 阻尼器高跨比相关性分析

直角型结构的阻尼器可能会受到钢板长度的影响,所以对阻尼器的高跨比——两侧约束钢板长度(高度)和中间剪切钢板长度(跨度)的比值进行研究。为了更好地探究高跨比对阻尼器滞回性能的影响,将其设为3种工况,分别为200 mm∶400 mm(1∶2)、400 mm∶400 mm(1∶1)、400 mm∶200 mm(2∶1)。橡胶层尺寸为100(长) mm×100 mm(宽)×6 mm(高),加载频率和位移幅值分别为2.0 Hz和30 mm。

3种高跨比工况下直角型黏弹性阻尼结构的变形如图18所示。由图18可知,当两侧约束钢板较长时,在固定端的另一端会产生较大位移,而中间剪切钢板的长短则对位移影响较小。

图18 不同高跨比的阻尼器位移图Fig.18 Displacement diagram of the damper with different height-span ratios

3种高跨比工况下阻尼器的滞回曲线如图19所示。由图19可知,高跨比为2∶1时,阻尼器的滞回环面积最大,最大阻尼力亦有所提高;在其他两种高跨比工况下,阻尼器的滞回曲线基本重合。阻尼器高跨比的增大提高了直角型黏弹性阻尼器的滞回耗能性能,可能原因在于大高跨比工况下钢板端部发生位移,起到了塑性耗能的作用,从而增大了其滞回耗能性能。

图19 不同高跨比工况下的阻尼器滞回曲线Fig.19 Hysteretic curves of the damper under different height-span ratios

7 结论

(1) 当频率为1.5 Hz时,NMK/FKM纳米复合材料宽阻尼温域和TA值皆达到峰值,该工况下材料的阻尼性能最佳;对直角型阻尼器而言,损耗因子和等效阻尼系数均在1.5 Hz频率下取得最大值,这种一致性一定程度上验证了数值模型的有效性。

(2) 各频率下阻尼器骨架曲线大致呈中心对称。在不同位移加载下,阻尼器的刚度未发生下降现象,在整个工作中状态良好。当阻尼器变形达到极限位移时,荷载仍未出现下降段,说明直角型阻尼器具有良好的变形和耗能能力。

(3) 直角型黏弹性阻尼器表现出刚度随位移幅值的增大而增大的动力特性。当频率为0.5、1.0和1.5 Hz时,阻尼器滞回特性表现为非线性类型;当频率升至2.0 Hz时,滞回特性则为线性。当频率为1.5 H时,损耗刚度、等效阻尼系数和损耗因子均达到峰值,最大阻尼力、存储刚度则在2.0 Hz时达到最大值。

(4) 在各位移幅值下,两块黏弹性材料层的应力分布基本对称,且随位移幅值的增大各处的应力也增大。应力的极值点均出现在与中间钢板连接处的边缘,且在材料层中心点处出现应力变化。钢板应力较黏弹性材料层的应力大得多,所有位移幅值工况下,钢板应力的极值点皆出现在钢板固定端的角点处,且应力对称分布,从钢板固定端向另一端呈发散式分布。

(5) 阻尼器高跨比的增大提高了直角型黏弹性阻尼器的滞回耗能性能,原因可能是在大高跨比工况下钢板端部发生了位移,从而增加了塑性耗能的作用。增大黏弹性材料层的厚度会降低阻尼器的滞回耗能能力,减小阻尼器的最大阻尼力和刚度。