非圆齿轮冲压机构优化设计与分析

2022-12-11黄志东

制造业自动化 2022年11期

黄志东

(辽宁科技学院机械工程学院，本溪 117004)

0 引言

冲压机构是一种常见的机械结构，通过多个不同的杆件，实现滑块的直线往复运动，最终达到冲压效果。文献[1]采用遗传算法实现了一种冲压机构的优化设计。文献[2]针对薄壁零件提出一种优化设计方法。文献[3]对比分析了三种对称多连杆式冲压机构传动特性。文献[4]分析了一种新型多连杆冲压机构的运动过程。然而，冲压机构在工艺行程中速度波动仍然很大，不同程度地影响冲压质量。

非圆齿轮能够实现变速运动，很多研究人员已经尝试将非圆齿轮与典型机构结合使用，如曲柄滑块、曲柄摇杆、摆动导杆以及Hoeken机构等[5～9]；将非圆齿轮应用到一些设备中，实现机构对速度的特殊要求，如牛头刨床、颗粒包装机、抽油机、移栽机构和差速泵等[10～14]。本文提出将非圆齿轮作为前置机构引入冲压机构中，力求实现冲压机构在工艺行程中速度更均匀，工作过程更平稳。

1 冲压机构数学模型

冲压机构矢量简图如图1所示。AB为曲柄，长度为l1，杆BC、CD、CE的长度分别为l2、l3、l4，滑块E沿铅垂方向运动。以点O为坐标原点，以OA方向为X轴正方向，以OD方向为Y轴正方向，建立坐标系。OA长为a，OD长为b，DE在Y方向的距离为c。杆AB与X轴正方向的夹角为φ，杆BC与杆CD之间的夹角为γ，杆CD与Y轴正方向的夹角为θ。

图1 冲压机构矢量简图

根据几何关系，可知A(a,0)，B(a+l1cosφ,l1sinφ)，D(0,b)，于是可推出：

由余弦定理，可得：

故可推出：

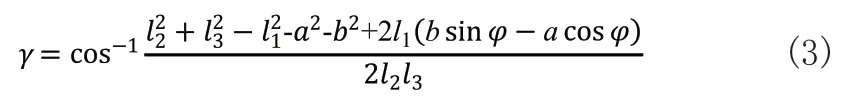
根据三角函数关系，可知：

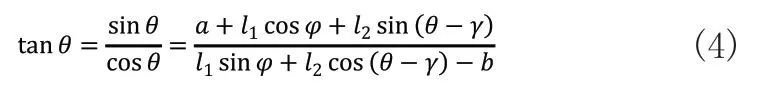
于是，可得：

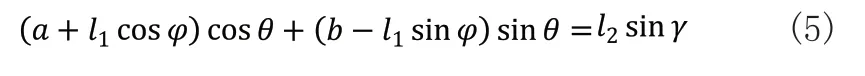
令

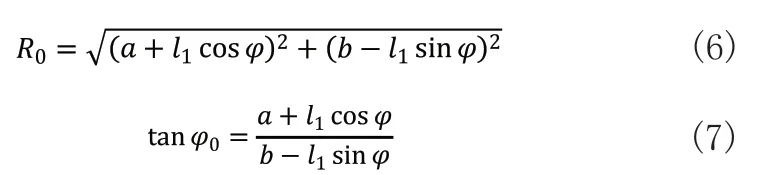
则有：

可得：

于是，可得点C和点E的坐标分别为：

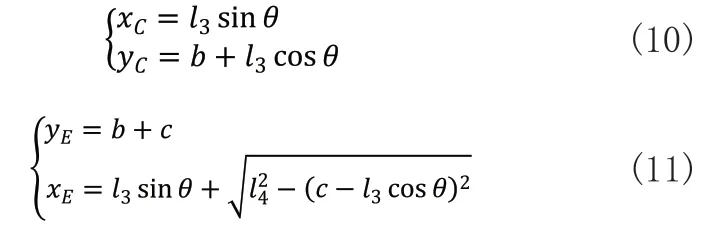
滑块E的速度为：

2 冲压机构运动特性分析

根据冲压机构基本参数[15](如表1所示)，可计算出γ、θ以及xE随φ的变化曲线，如图2～图4所示。

表1 冲压机构基本参数 mm

图2 γ-φ变化曲线

图3 θ-φ变化曲线

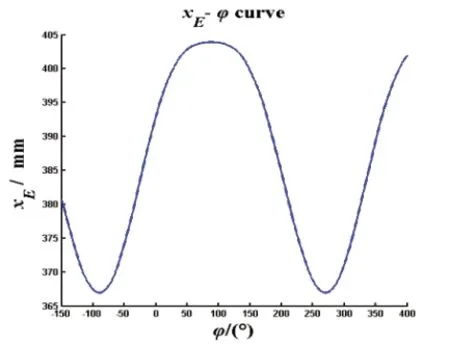
图4 xE-φ变化曲线

滑块的工艺行程对应φ的取值范围为58°～118°，由图5可知：xEmax=403.9096mm，xEmin=403.3325mm，∆xE=0.5771mm。

图5 滑块的工艺行程范围

当驱动杆AB的角速度ω=1°/s时，速度vE随φ的变化曲线如图6所示。

图6 vE-φ变化曲线

如图7所示，在工艺行程中，滑块E的速度在0附近波动，最大值为0.0498mm/s，最小值为-0.0472mm/s，速度极差为0.0996mm/s，平均值为8.0368×10-4mm/s，速度波动为5.8760×10-4(mm/s)2。

图7 工艺行程范围内的vE-φ变化曲线

3 椭圆齿轮基本理论

如图8所示，椭圆齿轮的回转中心在其上的一个焦点上。当主动齿轮转过Ф1角时，从动齿轮转过Ф2角，节曲线上转过的弧长相等。这时，主动齿轮的向径R1与从动齿轮向径R2之和应等于两轮的中心距，即R1+R2=A。

图8 椭圆齿轮副啮合传动简图

当以回转中心F1为原点，F1M方向为极轴时，则主动轮的节曲线方程式[16]为：

式(13)中Ф1为向径R1的极角；a为椭圆的长半轴；b为椭圆的短半轴；c为椭圆的对称中心到焦点的距离；e为椭圆的偏心率，e=c/a。

于是，可得：

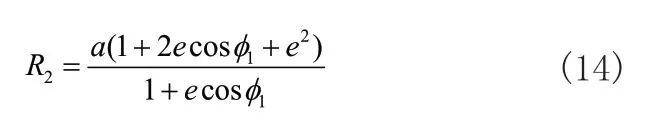
由式(13)和式(14)可得两齿轮的传动比函数为：

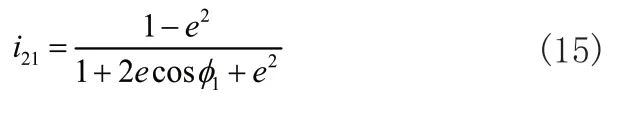
Ф1和Ф2之间的函数关系为：

4 非圆齿轮冲压机构优化设计与分析

4.1 非圆齿轮冲压机构优化设计

冲压机构的滑块在工艺行程中的速度稳定性决定了冲压质量，本文将可实现变速运动的非圆齿轮机构引入冲压机构中作为前置机构，两种运动复合后，对滑块的速度波动产生有效的调节，从而提升冲压机构的冲压质量。

分别以偏心率为0.1、0.2和0.3的椭圆齿轮为例，来优化冲压机构运动特性，优化后的各项参数如表2所示，速度曲线如图9～图11所示。

表2 非圆齿轮冲压机构性能参数

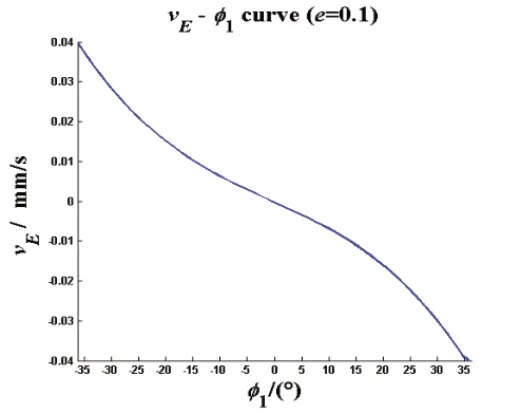
图9 优化后vE-Φ1变化曲线(e=0.1)

图10 优化后vE-Φ1变化曲线(e=0.2)

图11 优化后vE-Φ1变化曲线(e=0.3)

4.2 运动特性分析

椭圆齿轮偏心率一般不超过0.7，根据4.1部分的方法计算出偏心率为0.4、0.5和0.6时的优化结果，对比普通冲压机构的相关参数，速度极差、平均速度和速度波动随偏心率变化曲线如图12～图14所示。

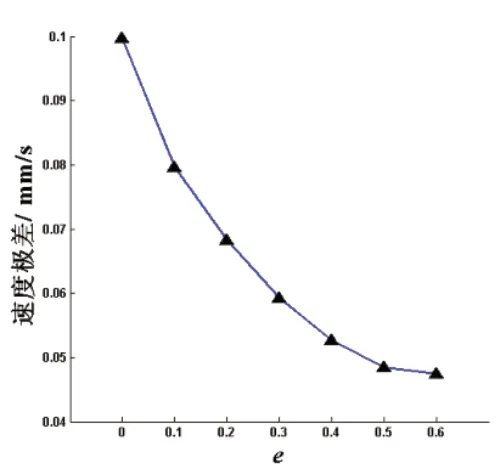
图12 速度极差变化曲线

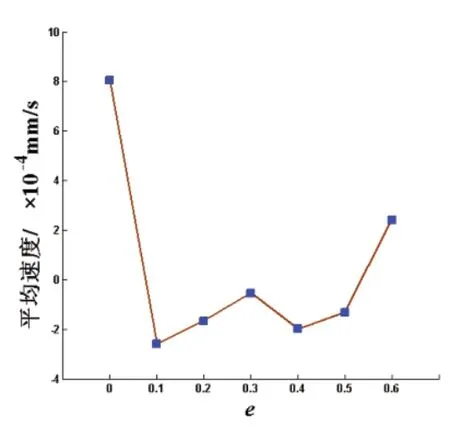
图13 平均速度变化曲线

图14 速度波动变化曲线

由图12可知，与普通冲压机构相比，优化后的速度极差显著下降，且随着e的增大，速度极差逐渐减小，当e达到0.3后，速度极差的变化不明显；由图13可知，与普通冲压机构相比，优化后的平均速度明显更接近于0，其中e为0.3时最为理想；由图14可知，与普通冲压机构相比，速度波动大幅降低，且e越大，速度波动的降低程度越小。结合以上优化结果和各项指标规律，综合考虑椭圆齿轮机构运动稳定性以及椭圆齿轮加工等问题，建议选择偏心率在0.2～0.3之间的椭圆齿轮作为冲压机构的前置机构，实现冲压机构滑块在工艺行程内速度更加稳定，从而提高冲压质量。