基于激光扫描臂的机器人操作的样品定位方法
2022-12-11郭惟伟李群明刘啸文吴波
郭惟伟,李群明,刘啸文,吴波
(1.中南大学 机电工程学院,长沙 410083;2.中南大学 轻合金研究院,长沙 410083;3.中南大学 高性能复杂制造国家重点实验室,长沙 410083)
0 引言
材料与构件深部应力场及缺陷无损探测中子谱仪用于探测样品(材料/构件)深部残余应力场和宏观应力场、构件损伤缺陷及周围应力场以及材料组成相应力[1]。其测量原理如图1所示,高速中子束流从入射狭缝引出,向样品照射,当与样品内部的材料晶面满足布拉格条件[2]时,发生衍射,通过探测器探测衍射的中子束流强度即可得到衍射峰,研究衍射峰的位置与强度即可得到散射矢量Q方向上的应力的相关数据[3]。

图1 中子衍射测量残余应力的原理图
目前,广泛用于中子衍射测量的运动平台主要为四轴样品台[4~7],其定位方法简单且定位精度较高,但灵活性不够,在测量样品内部多个方向的残余应力时,往往需要对样品进行二次装夹[8]。工业六轴机器人具有通用性强、灵活性高、性能稳定、重复精度高等优点,因此,对于较小的样品(20kg以内),可应用六轴机器人操作并进行残余应力的测量,其优点在于无需多次装夹,且六个自由度的运动可满足不同方向的应力测量需求,测量效率高。
利用中子衍射测量样品的残余应力需要满足的定位条件是实现样品上的待测量点与测量参考点对齐,待测矢量与散射矢量对齐。即测量样品时需要将待测量点移动到衍射点进行测量,并利用中子入射束与中子衍射束和机器人的相对位姿关系对样品进行精确定位。针对样品台操作的样品定位,韩志强[9]提出了一种基于双全站仪的样品台位姿标定方案,其定位精度较高,但操作复杂。针对中子衍射测量过程中样品位姿的确定,徐舟[10]提出了一种基于基准球的样品位姿标定方法,适用于中子衍射测量过程中规则样品与复杂曲面样品的位姿快速标定,但精度较低,受人为因素的影响大。
无接触测量方式的激光扫描臂具有测量精度高、使用方便和受人为因素的影响小等优势。因此,本文提出了基于激光扫描臂标定的样品定位方法,其不仅操作便捷,可以实现精确、高效率的样品定位测量,而且在满足定位条件的同时,实现多种样品位姿的应力测量。
1 机器人的运动学模型
1.1 正运动学模型
本文以瑞士Staubli公司的TX90机器人为研究对象,其几何结构及根据D-H法[11]建立的参考坐标系如图2所示,则可以得到如表1所示的D-H参数,其中,关节变量θi表示沿Zi-1方向上Xi-1和Xi之间的夹角;关节偏移di表示沿Zi-1方向上Xi-1和Xi之间的距离;连杆长度ai表示沿Xi方向上Zi-1和Zi之间的距离;扭转角αi表示沿Xi方向上Zi-1和Zi之间的夹角,i=1,2,…,6。
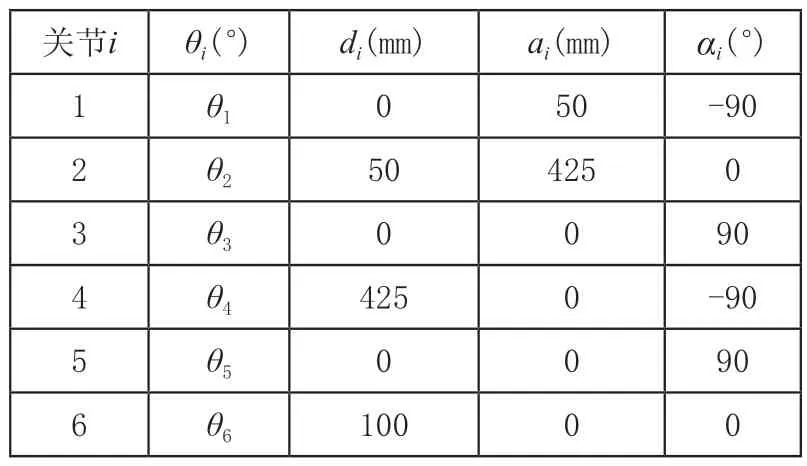
表1 机器人的D-H参数

图2 TX90机器人
由D-H模型可得机器人的两相邻坐标系之间的位姿变换矩阵为:

那么,机器人的末端坐标系相对于基坐标系之间的位姿变换矩阵为:
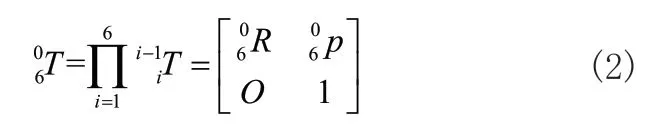
式(2)即为机器人的正运动学模型,它描述了机器人的末端坐标系在基坐标系下的位置和姿态,为3×3矩阵,表示机器人的末端坐标系相对于基坐标系的旋转变换,为3×1矩阵,表示机器人的末端坐标系相对于基坐标系的平移变换。
1.2 逆运动学模型
在机器人操作样品进行中子衍射测量的过程中,测量参考点与散射矢量相对于机器人的位置是确定的,为了使位于机器人末端的样品到达期望位姿以满足衍射测量的定位条件,需要利用标定得到的测量参考点与散射矢量获得使样品的定位满足定位条件的机器人末端位姿矩阵,然后计算机器人的运动学逆解,从而获得相应的关节运动指令。考虑到矩阵的未知变量较多,本文提出一种先旋转后平移的机器人位姿计算方法,该算法可实现使任意待测矢量与散射矢量精确对齐的位姿矩阵的求解,并为样品的应力测量姿态优化提供基础。
如图3所示,已知测量参考点在机器人的基坐标系{0}上的坐标为0PM;通过测量参考点的散射矢量在机器人的基坐标系{0}上的坐标为0Q;与机器人末端固连的样品坐标系{S}与机器人末端坐标系{6}的位姿变换矩阵为待测量点在样品坐标系上的坐标为SP;通过点的待测矢量在样品坐标系下的坐标为SV,这些坐标系与位姿变换矩阵均可通过激光扫描臂标定获得。机器人需要将位于末端样品上的待测量点SP移动到测量参考点0PM的位置,且使待测矢量SV对齐于散射矢量0Q。

图3 机器人操作样品的定位示意图
根据以上条件可建立机器人的位姿求解模型:

将式(3)简化为:


图4 待测矢量6V对齐于散射矢量0Q
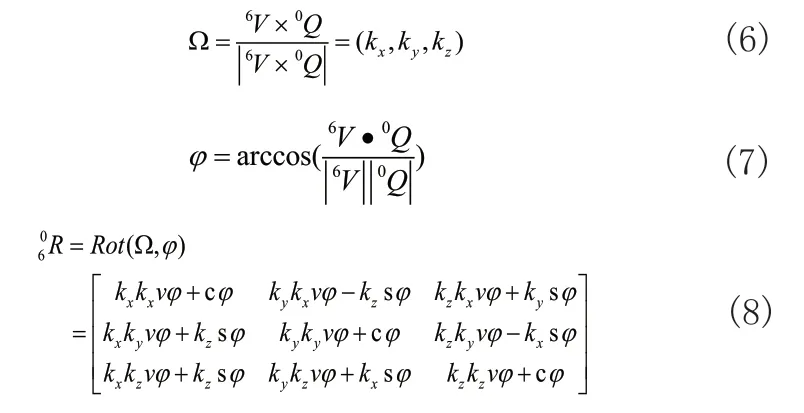
其中,vφ=1-cosφ。Rot(Ω,φ)为向量6V绕着Ω轴线旋转角度φ的等效旋转矩阵[12]。将代入式(4)即可解得机器人末端位姿矩阵。
由于在进行中子衍射测量过程中,应尽量让中子束直接照射样品而不被夹具或者机器人自身遮挡,且入射狭缝与衍射狭缝的出口距离样品表面较近,因此,已求解得到的机器人末端位姿虽然可以满足定位条件,但并不一定可以让样品顺利完成残余应力的测量。而且更多满足定位条件的机器人末端位姿可以为残余应力测量过程提供多种选择,提高了测量的灵活性,有利于机器人在中子衍射测量中的位姿规划。
为了获得其它满足定位条件的机器人末端位姿,可让末端坐标系{6}绕散射矢量0Q旋转α角度,得到的坐标系{6'}与基坐标系{0}的位姿变换关系:

式(9)中,改变旋转角度α,即可获得不同的机器人末端位姿矩阵。
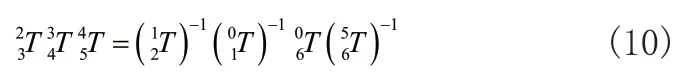
令等式两边矩阵的对应元素相等,即可求解得到与机器人末端位姿矩阵对应的6个关节角(θ1,θ2,θ3,θ4,θ5,θ6)的值。
2 坐标系的标定
2.1 机器人末端坐标系的标定

图5 激光扫描臂

图6 机器人的末端坐标系

2.2 样品坐标系的标定
样品坐标系的建立将为样品上的待测量点在机器人基座标系的位置确定提供参照。将样品与探针通过夹具安装到关节角处于q0状态下的机器人末端,探针的作用是确定参考点在机器人基座标系下的位置。利用激光扫描臂扫描样品与探针,获得样品与探针的点云模型,提取样品的特征点,在Polyworks中建立样品坐标系,记为{S},如图7所示,可以得到样品坐标系{S}相对于测量臂的世界坐标系{R}的齐次坐标变换矩阵。所以,样品坐标系相对于机器人末端坐标系的齐次坐标变换矩阵:
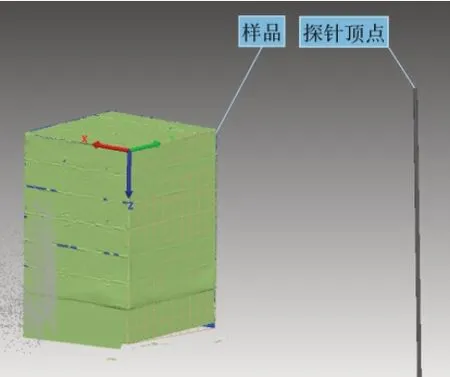
图7 样品与探针的点云模型

在Polyworks中依据探针的点云模型建立探针顶点特征即可得到探针顶点e在机器人末端坐标系{6}中的坐标6Pe。
2.3 中子衍射坐标系的标定
装置规范体积(IGV)是实际中子束通过限束孔后所形成的空间体积,测量参考点是这个体积的几何中心[14]。测量参考点位置的标定需要利用中子束对探针顶点进行扫边测量,以确定测量参考点在机器人基坐标系下的坐标,从而标定衍射坐标系{M},为残余应力测量过程中的样品定位提供参照。考虑到中子入射束和衍射束的特殊性、高成本等因素,本文采用激光束模拟中子衍射束与入射束,如图8所示。

图8 中子衍射坐标系的标定
打开激光,利用示教盒控制机器人将探针顶点移动至参考点,此处为两束激光的交汇点,读取此时机器人关节编码器反馈转角qM,将此时的机器人姿态称为机器人的衍射姿态。由机器人的正运动学可得机器人的姿态矩阵此时探针顶点的位置即为参考点的位置。
由于探针顶点在机器人末端坐标系中的位置6Pe已知,因此参考点M在相对于机器人基座标系的位置为:
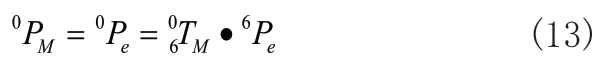
利用激光扫描臂扫描入射狭缝与衍射狭缝,此处为两束激光的出射口中心,通过Polyworks提取特征点,并激活机器人基座标系即可得到入射狭缝与衍射狭缝在机器人基座标系中的位置分别为:0PI、0PJ。
在Polyworks中构造“平面-直线-点”特征即可建立中子衍射坐标系{M},如图8所示,其中,原点可依据参考点0PM的坐标以数字化创建点的方式确定,X轴为向量在水平面上的投影,Z轴通过参考点且垂直于水平面向上,Y轴依据右手系规则确定。
散射矢量即为待测量点的残余应力测量的目标方向。由于散射矢量是中子入射束和中子衍射束的角平分线,所以散射矢量在机器人基座标系中的向量表示为:
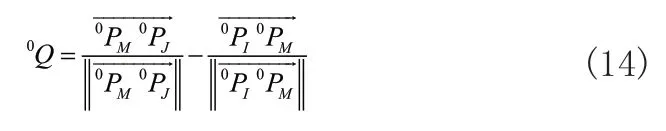
3 样品定位实验
3.1 移动待测量点至参考点
在样品内部设置如图9(a)所示的点为待测量点,点的位置与待测矢量在样品坐标系上的坐标值如表2所示。

表2 样品坐标系上的待测量点与待测矢量

图9 待测量点的定位
3.2 样品的定位精度分析
为了进一步研究样品的定位精度与机器人姿态间的关系,优化样品的应力测量位姿。本文设置样品坐标系的原点为待测量点,沿3个坐标轴负方向为待测矢量。由机器人的逆运动学模型可知,对于样品上每个待测量点的残余应力测量,都有多组机器人姿态满足其定位条件。取其中的20组不同姿态下的待测量点与待测矢量,利用激光扫描臂测得它们在激光扫描臂的世界坐标系中的坐标值,并和参考点与散射矢量在机器人的基坐标系中的坐标值对比,可以得到图10所示的数据结果。其中,0Pi=(0xi,0yi,0zi)表示第i个机器人姿态下的待测量点在机器人基座标系下的坐标,0Vi=(0vxi,0vyi,0vzi)表示第i个机器人姿态下的待测矢量在机器人基座标系下的坐标,Δdi表示第i个机器人姿态下的待测量点与参考点的坐标综合偏差,Δγi表示第i个机器人姿态下的待测矢量与散射矢量的角度偏差,qi=(θi1,θi2,...,θi6)表示第i个机器人姿态,qM=(θM1,θM2,...,θM6)表示衍射姿态,ΔSi表示姿态qi与姿态qM的关节空间上的欧式距离,计算公式如式(15)~式(17)。其中,i=1,2,…,20。
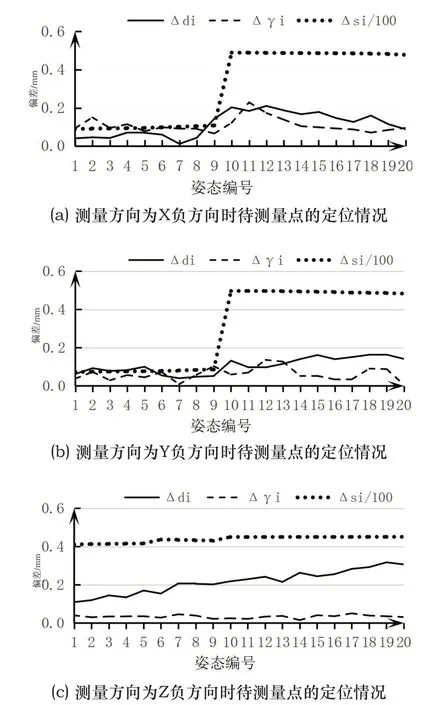
图10 3个不同测量方向的待测量点在20组不同的机器人姿态下的定位情况

由图10(a)、图10(b)可知,机器人从第9个姿态到第10个姿态时待测量点的定位综合偏差均有明显的上升,且两个姿态相对于衍射姿态的欧式距离也有明显的变化,而图10(c)中待测量点的定位综合偏差随着当前姿态相对于衍射姿态的欧式距离的增大而增大,即3个方向的测量中机器人处于姿态1~9时待测量点的定位综合偏差普遍比机器人处于姿态10~20的定位综合偏差较小,且机器人处于姿态1~9的欧式距离普遍比机器人处于姿态10~20的欧式距离较小。因此,在机器人参与中子衍射残余应力测量的过程中,其定位误差和机器人的测量姿态与衍射姿态间的欧式距离呈正相关。所以,机器人参与样品的残余应力测量过程中,为了优化样品的应力测量位姿,应尽量选择与衍射姿态的欧式距离较小的机器人姿态。
4 结语
本文针对以机器人作为运动平台实现样品在中子衍射残余应力测量过程中的精确定位,建立了机器人的运动学模型,并针对样品的定位条件提出了一种先旋转后平移的机器人位姿计算方法。设计了机器人的基座标系、样品坐标系以及衍射坐标系的激光扫描臂标定方案。根据定位需求结合各坐标系间的位姿关系、机器人的运动学模型计算机器人的运动学逆解,并对样品的测量位姿进行优化,生成关节运动指令,从而实现待测量点移动至参考点的残余应力测量。实验结果表明,此定位方法精度较高且测量方便,可提高样品在中子衍射测量残余应力中的定位效率,充分地发挥机器人在中子衍射残余应力测量中的优势。
