基于键合图法对定轴轮系模块化建模及稳定性研究

周新涛，马娜，崔亚辉

（1.陕西工业职业技术学院 机械工程学院，咸阳 712000；2.西安理工大学 机械与精密仪器工程学院，西安 710048）

0 引言

齿轮传动系统是机械设备的扭矩、功率传递的核心部件之一，其系统精确动学行为的研究尤为重要[1,2]。当前，随着科技的发展，导致实际应用对齿轮传动系统的各项综合性能的要求越来越高，从而使齿轮传动系统的结构形式变得也越来越复杂[3,4]。当轮系的结构越复杂，对系统传递功率特性的不特定性增强，其系统动力学行为的研究越发困难。采用传统的建模研究方法，如牛顿第二定律法、等效集中质量法和有限元法等，这些方法对复杂轮系的动力学模型有很大难度[5]。另外，通常这些方法建立起来的数学模型，其模型在建立时也是经过大量等效与简化处理，所得出的计算结果只是轮系动特性的近似解[6]。当轮系结构的复杂性较大时，系统参数对系统动力学特性的灵敏性较大，任何细微的变化或波动，均能引起系统的解析解或数值解产生巨大扰动，从而导致对轮系动态特性的研究失败[7]。因此，采用上述传统的建模法，得出系统的近似特性，难以解释轮系动态特性研究的需求。

为了解决传统建模法，难以得出轮系的精确化数学模型的问题。本文通过对轮系传动结构的大量研究，根据轮系最小传动单元的结构属性，将结构复杂的定轴齿轮传动系统拆分为由多个基本的模块组成的理念。引入模块化的建模思想，研究定轴轮系的建模方法和系统的动力学行为。另外，经大量研究与总结，可知现代图论法[8,9]、信号流图法[10～12]和键合图法[13,14]等，具有高效、准确的建模优势。但是，前两种方法的理论体系尚不成熟，对最终的计算结果难以有权威评价。而键合图法具有完善的理论体系和丰富的图元库，可用于复杂的多能域系统的综合性能研究中。故此，本文结合键合图的建模机理，建立出基本模块的键合图模型。然后，在基本模型键合图模型的基础上，按照轮系中功率流的传递方向进行扩展，从而得出轮系完整的精确化数学模型。最后，根据此模型可推导出该系统的动力学状态方程，并通过数值计算后能准确的掌握系统的力学特性和运动学特性，为后续深入研究系统的非线性特性奠定基础。

1 键合图建模法简介

在工程生产中，键合图法对多能域复合场相关特性参数计算，是一种最高效、最重要地方法。该法已经过了漫长的研究与发展，其理论方法的应用也逐步趋于成熟。另外，对多能域复杂系统动态性能的研究，采用传统方式建模与研究时，难以准确地反映出该系统动特性的真实情况。而键合图法利用自身强大的图元库和灵活的建模方式，能模拟出各种类型能量系统中线性或非线性的相关特性。图元要素，如表1所示。

表1 键合图的基本图元库

2 单级定轴轮系的键合图模型

定轴单元体可以看作是由多级不同齿轮的啮合而构成的系统，一对相互啮合的齿轮又是这个系统中最小的传动单元。在本节处建立定轴单元体的键合图模型，是以这组最小传动单元为载体，其动力学模型的示意图，如图1所示。其中，在图中字符的含义分别是：O1为主动齿轮，O2从动齿轮；x1(t)、x2(t)分别为轮齿啮合线上的相对位移；T1、T2分别是输入、输出转矩；θ1、θ2分别是主、从动齿轮的角位移；k为轮齿啮合刚度；C为轮齿啮合阻尼；J1、J2分别是主、从动齿轮的转动惯量；e1(t)为轮齿综合啮合误差；R1和R2分别是齿轮O1、O2分度圆半径。

图1 单级齿轮传动系统的动力学模型

研究机械系统真实的运动情况，必须先要分析出机械系统的功能关系。采用合理的数学模型，建立作用于系统的外力与系统动力学参数和运动学参数之间的对应关系式。对于图2所示的动力学模型，点A、B其实是齿轮O1、O2啮合分度圆上的一个共有点P，落在齿轮O1上的半边点为A，落在齿轮O2上的半边点为B。根据三心定理可知，点P为这对相啮合齿轮O1、O2的相对速度瞬心点。存在的关系为：VP1=VP2，亦即VA=VB。则有：

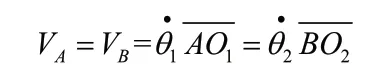
即，单级齿轮传动系统的运动学关系（系统的瞬时传动比i），如式(1)所示：

因此，根据式(1)可知，在单级齿轮传动系统中有2个绝对速度点和1个相对速度点构成。然后，再依据键合图建模的基本原理，可知该系统中需要3个1-结，以及1个二通口的TF元件。最后，得出单级齿轮传动系统的键合图模型，如图2所示。

图2 定轴单元体的键合图模型

3 定轴轮系模块化键合图模型的扩展

3.1 两级定轴轮系的键合图模型

如图3所示是定轴单元体的两级齿轮传动形式，图中：齿轮O1、O2、O3和O4的分度圆半径分别为R1、R2、R3和R4，J1、J2、J3和J4分别为这4个齿轮的转动惯量。齿轮O1与O2轮齿啮合的稳态刚度为k1(t)，齿面阻尼为C1，稳态传动误差为e1(t)。齿轮O3与O4轮齿啮合的稳态刚度为k2(t)，齿面阻尼为C2，稳态传动误差为e2(t)。

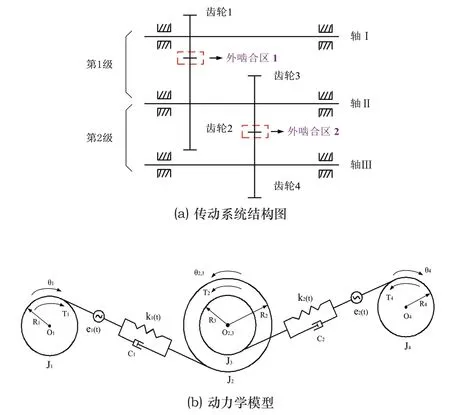
图3 定轴单元体的两级齿轮传动系统

图4所示是定轴单元体的两级齿轮传动系统的键合图模型，该轮系的稳态传动误差导数作为流源分别作用于该系统中，如图中的键Sf8、Sf19。两组啮合齿轮的稳态啮合刚度k1(t)、k2(t)，均采用容性元件C来模拟，如键C28、C32。两组啮合齿轮的齿面阻尼C1、C2，均采用阻性元件R来模拟，如键R29、R33。输入轴I、中间轴II和输出轴III的转动刚度的模拟量分别为C26、C30和C34，扭转阻尼的模拟量分别为R27、R31和R35。

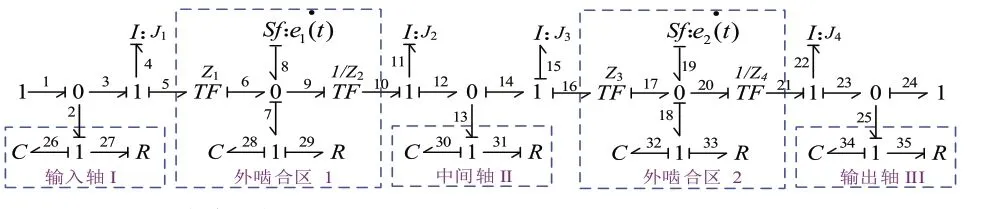
图4 定轴单元体的两级齿轮传动系统的键合图模型

3.2 多级定轴轮系的键合图模型

定轴单元体模块化的扩展是比较简单，其扩展形式如图5所示。当该模块的输入ωIn、输入参数ωOut，以及各齿轮的齿数Zi等参数已知时，可根据定轴轮系的计算关系就能计算出定轴单元体模块的等效特性。

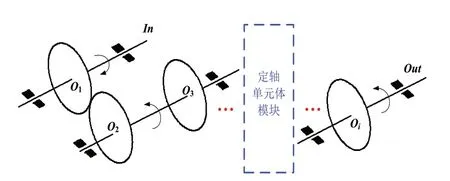
图5 定轴单元体的结构扩展示意图

同理，图6所示的是定轴单元体的结构扩展轮系的键合图模型，该轮系的键合图模型是在图4的基础扩展而来。因此，在此处将不再做详细说明。

图6 定轴单元体的结构扩展轮系的键合图模型

4 状态方程

4.1 系统状态方程的描述原理

根据键合图模型中，各能量元件的相互连接关系和功率流传递的情况，可将键合图模型本身隐含着描述系统特性的状态方程给列写出来。本部根据上述P型单元体的键合图模型，列写该系统的状态方程。

其线性系统的状态方程的基本形式可写成，式(2)所示的形式：

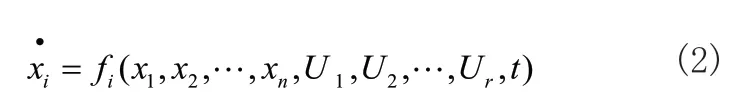
式(2)中，xi(i=1,2,…,n)为状态变量；Uj(j=1,2,…,r)是系统的输入变量；fi()是代数函数；t是时间变量。

4.2 单级定轴轮系的状态方程

根据图2所示定轴单元体的键合图模型，再以惯性元件I的广义动量p与容性元件C的广义位移q为状态变量。该键合图中含有三个容性元件：C15、C17、C19，以及两个惯性元件：I4、I11，且这些元件皆具有积分因果关系。即可得出P型单元体的状态变量Y=[p4,p11,q15,q17,q19]T。根据P型单元体键合图模型的因果关系和功率流向等条件，可得出用于描述定轴单元体运动状态的状态方程，如式(3)～式(7)所示：

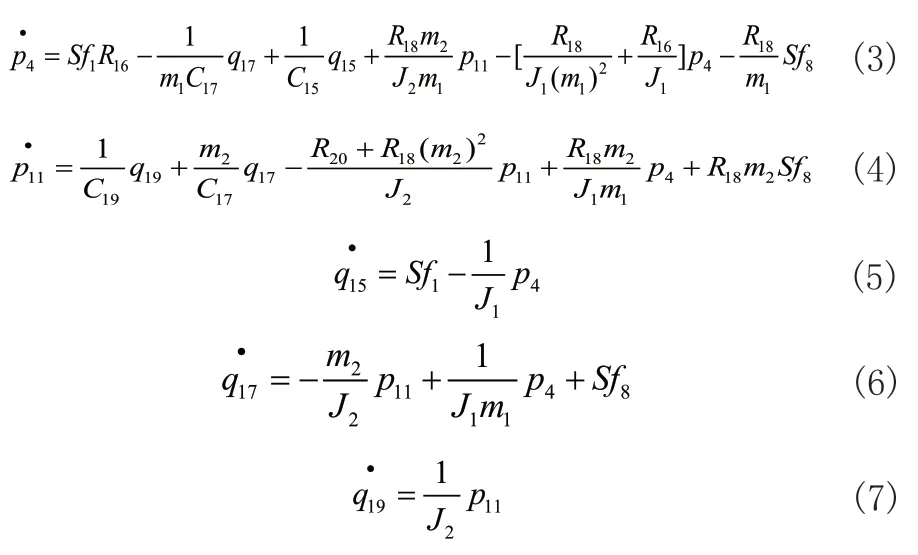
式(3)～式(7)中，m1、m2为分别为两啮合齿轮的齿数Z1、Z2；Se1为向系统中输入的势源；Sf8为稳态传动误差的导数，即向系统中输入的流源。

设，该系统的输入变量矩阵为U，以及参数矩阵A、B，其具体表示形式如下所示：

则，P型系统的状态方程可写成矩阵形式，如式(8)所示：

5 系统动态特性仿真分析

5.1 仿真条件设置

根据图2所示的键合图模型，采用数值仿真软件构建出P型单元体的仿真模型，如图7所示。图中，MSe表示轮系的输入力矩，仿真中采用持续信号输入系统；MSf表示啮合传动的稳态误差函数；Rv表示系统外的阻力矩。

图7 P型单元体的仿真模型

其中，仿真参数设置为：齿数Z1=16，Z2=24；弹性模量E=2.1E11(N/m2)；泊松比μ=0.3；齿轮惯性矩I1=0.041(Kg·m2)，I2=0.079(Kg·m2)；轴的扭转刚度K=2E8(N/m)；轴承的支撑阻尼Cv=1800(N·s·m-1)；轮齿啮合阻尼Cg=2000(N·s·m-1)；轮系系统的输入力矩为TI=470(N·m)；系统外部的阻力矩TO=320(N·m)；稳态传动误差的导数0.0027 ×cos(28t+21pi)。

5.2 系统传递函数

根据图2中给出的P型单元体的键合图模型，可得出该单元体系统传递函数的一般表达式G(s)p，如式(9)所示：

式(9)中，s为拉氏算子；a、b为系统参数与系统的初始状态和特性有关。

5.3 仿真结果分析与探讨

从图8(a)中可以得出，闭环系统的开环传递函数的一对极点和零点等于0。一般习惯上，将系统开环的0根作为左根处理。并且，这对极点和零点构成了偶极子而相互消除。且该系统的开环传递函数的极点和零点，均在复平面[S]的左侧，故该系统为最小相位系统。从图8(b)所示的Bode图中得出，系统的相位裕量γ(ωc)=90deg＞0，幅值裕量Kg=307dB＞0。幅值穿越频率上的斜率为-20dB/dec，从而保证了故能说明该系统是稳定的。由图8(c)所示的Nyquist图中得出，该系统的开环频率特性曲线不包围（-1，j0）点，且开环无右极点，故根据Nyquist稳定性判据可得该系统稳定。同时，也说明了该系统传递函数以惯性环节为主导。由图8(d)所示的Nichols图，纵轴是幅值的对数，横轴是相角，该图反映了幅值与相角的变化关系。采用该图也能进一步说明P型单元体在此种模拟工况下，其闭环系统是稳定的。

图8 P型单元体系统的稳定情况

6 结语

针对结构复杂的齿轮传动轮系，采用传统建模法难以快速、准确地得出轮系精确化数学模型的问题。本文提出将结构复杂的轮系拆分为由多个基本模块叠加的方式组成，在此基础上根据键合图法的建模原理，建立起模块化的键合图模型。然后，根据轮系的结构特征，将模块化的键合图模型按照轮系传递功率流方向进行扩展，从而建立出复杂轮系传动系统的完整键合图模型。最后，通过数值仿真法，模拟了基本模块的动力学行为，并得出了其系统的动态指标。仿真表明，采用此法可提升结构复杂轮系精确化数学模型的建模效率和精度，也能为后续轮系的非线性动力行为进行深入研究奠定基础。