结合改进CNN和双约束损失函数的叠前地震数据低频补偿方法

戴永寿 高倩倩 孙伟峰 万 勇 吴莎莎

(中国石油大学(华东)海洋与空间信息学院，山东青岛 266580)

0 引言

中国油气勘探目标已由中、浅层逐渐转入深层、超深层[1-2]。在西部地区，以岩溶缝洞型、礁滩孔隙型、白云岩孔隙型和裂缝型为代表的特殊油气藏，多具有圈闭复杂和储层多样的特征[3-4]，对地球物理勘探技术提出了严峻的挑战，包括地表、地下“双复杂”构造的成像、地震信号随深度增加发生非线性吸收衰减、低信噪比导致低频有效信号受损等。低频有效信号的缺失会导致地震剖面上出现虚假的高分辨率现象，从而降低后续地震反演、解释的精度。因此人们提出了诸多地震数据低频补偿方法。

基于模型驱动的低频补偿方法主要分为三类。第一类为基于褶积模型的低频补偿方法。毛博等[5]利用不同区间内反射系数序列与整体反射系数序列近似的这一现象，直接在频域将已知子波的低频分量与缺失低频成分的某区间内反射系数相乘得到重构的低频分量；Yang等[6]通过求解L1范数正则化线性反问题估计格林函数，再将格林函数与假设子波褶积重构低频数据。该类方法依赖子波为已知的假设。第二类为基于压缩感知的低频补偿方法。韩立国等[7]和宋亚民等[8]利用压缩感知求得反射系数振幅谱，再截取反射系数的低频部分与原始信号其他部分的振幅谱进行幅值匹配，进而补偿地震数据低频成分；丁燕等[9]在压缩感知理论基础上提出自适应L1范数权重因子求取方法并构建改进的宽带俞式低通整形滤波器。第三类为基于波动方程的低频补偿方法。依赖地震记录的包络包含丰富的低频信号[10]，王鹏[11]通过提取地震数据中反映大尺度信息的地震包络对常规地震数据的低频成分进行补偿。另外，妥军军等[12]针对三维地震数据提出二元插值方法，该方法适用于对空间上剧烈变化的目的层段的低频补偿处理；张红军等[13]应用GeoEast系统形成了一套低频配套处理技术；公亭等[14]提出基于扫描信号的频宽补偿方法，该方法通过对零相位化后的理论与实际输出进行匹配处理得到整形算子，再进行补偿。虽然上述方法可以有效补偿低频，但仍存在依赖严格假设、参数调整不灵活或成本较高的问题，以致低频补偿效率较低，在实际中应用受限。

深度学习近年来在各个领域中的应用已较为成熟，这种基于数据驱动的方法也逐渐应用于地震数据处理领域。Ovcharenko等[15]利用人工神经网络，通过中高频数据外推低频数据，但由于模型参数调整的局限性，容易导致补偿后高频段细节信息的损失；Sun等[16]利用深层卷积神经网络(CNN)从带限数据中自动恢复缺失的低频；毛博[17]利用CNN通过地震记录中频成分分别外推低频和高频成分；Ovcharenko等[18]利用U-Net网络将中频段时域图像分段映射到低频段实现低频补偿；Wang等[19]利用U-Net网络针对不同频带和采样间隔的地震数据进行低频补偿；Ovcharenko等[20]提出采用迁移学习方法通过重新训练轻量化网络MobileNet减少最优架构搜索和初始网络训练的计算量，以从单炮集的频域中推断出低频数据，并根据正则化反演对低频成分进行有效且准确的判断；Nakayama等[21]利用U-Net网络，输入三维矩阵训练，可同时实现信噪分离、缺失道重建和低频补偿。

由于单道地震记录训练样本集的幅值差异较小，且均方误差(MSE)损失函数求得的网络输出和标签之间误差的数量级也较小。因此，CNN在低频补偿中的应用仍有两个亟需解决的问题，一是梯度消失导致低频欠补偿；二是网络容易过早收敛导致低频补偿精度低。为解决CNN在低频补偿中存在的不足，并进一步提高网络的特征提取能力，本文提出一种结合改进CNN和双约束损失函数的叠前地震数据低频补偿方法。对合成地震数据和中国西部X地区实际叠前地震数据进行低频补偿，并与基于CNN的低频补偿方法和反褶积结合宽带俞式低通滤波器的低频补偿方法对比，验证本文方法补偿的低频有效信号优势。

1 结合改进CNN和双约束损失函数的低频补偿方法

本文提出的地震数据低频补偿方法分为神经网络训练阶段和实际地震数据处理阶段。首先，使用高通滤波器滤除合成地震记录低频成分，建立缺失低频的地震记录训练样本集；然后，将训练样本集输入到改进CNN模型进行训练，得到可以实现低频补偿的网络模型；最后，将缺失低频地震数据输入该网络，获得低频补偿后的高分辨率地震数据。

1.1 改进CNN的低频补偿原理

由于时域地震记录缺失低频成分，导致低频补偿前、后幅值差异较小，往往需要采用深层CNN提取更高层次的特征。而随着网络层数的增加，网络每一层提取的信息越来越多、参数量急剧增长，采用梯度下降法更新网络参数时容易出现梯度消失问题，使权重和偏置无法继续得到更新，以致网络难以学习到细微差异，从而导致低频欠补偿。

为解决上述问题，提出一种对网络结构的改进方法，在不提高CNN计算复杂度的前提下，加入可直接学习输入与输出之间残差特征的网络单元，将其定义为残差块[22-23]，主要由卷积(Conv)层、批归一化(BN)层和跳跃连接组成。如图1所示，x表示上一层网络的输出即残差块(ResBlock)的输入，f(x)表示单个残差块中卷积层的输出，F(x)=f(x)+x为残差块的输出，经非线性激活函数Relu后作为下一层输入。右侧是x的跳跃连接，可使网络某一层的输出不仅作为下一层的输入，而且可以跨过几层作为后面层的输入，从而缓解层数增加带来的梯度消失问题。同时，残差块中使用的BN层可在每层输出对采样的一小批数据都进行数据归一化处理，使下一层的输入数据量纲一致，使网络对细微特征变化更敏感，从而提高网络的收敛速度并降低模型对网络初始化的要求。

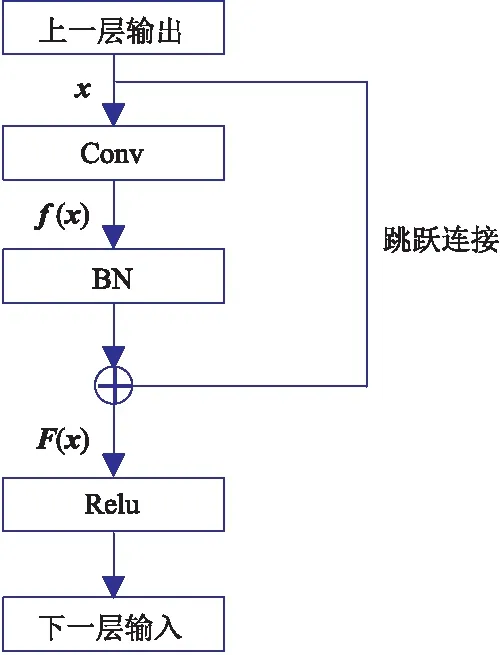
图1 残差块结构

本文构建的网络架构如图2所示。在经过两部分卷积层处理后初步提取到地震记录的低层次幅值特征，然后加入残差块，使网络可以提取到更高层次幅值特征，并减少多层卷积、池化(MaxPool)的压缩、采样操作带来的特征损失，避免梯度消失。最后经全连接层(Fully Connected Layers, FC)恢复至原始数据维度后输出。

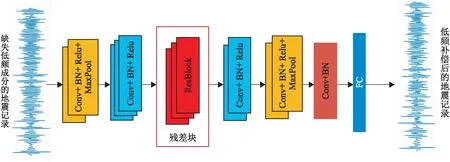
图2 改进的CNN网络架构

1.2 双约束条件下的损失函数

损失函数是计算网络预测值和真实值之间误差的函数，是深度学习中用来衡量网络模型品质的指标之一，决定了反向传播过程中梯度下降的方向，通过不断地训练、优化使损失函数值达到最小，最终得到最优的网络模型。地震数据的低频补偿属于非线性回归问题，通常使用均方误差作为损失函数，即

(1)

式中：n表示地震记录长度；di和Di分别表示原始地震记录d和低频补偿后的地震记录D在i时刻的值。

均方误差损失函数虽然可以较好地反映预测值和真实值之间的差异，但由于时域地震信号的幅值差异数量级较小，梯度变化不明显，造成网络过早收敛从而陷入局部最优，导致低频补偿精度低。为解决这一问题，以原始与低频补偿后地震记录的差异和相关度为优化目标，提出一种改进的损失函数，即通过均方误差与皮尔逊距离的加权和建立双约束条件下的损失函数计算补偿误差。

皮尔逊相关系数是用来度量两个信号之间的相关度。首先通过计算协方差函数求得相关度，然后除以标准差是为了将变量统一到相同数量级下，避免数据量纲差异导致损失函数的振荡，影响网络的学习能力，可用来衡量原始与低频补偿后地震数据的相关度，其表达式为

(2)

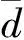
由于皮尔逊相关系数值越大，相关度越高，而神经网络训练时损失函数的值越小模型越优，因此使用皮尔逊距离1-ρd,D作为损失函数的一部分，与MSE的加权和作为损失函数

L=λ1MSE+λ2(1-ρd,D)

(3)

式中λ1和λ2为权重系数。

在保证MSE和皮尔逊距离所求值数量级一致的前提下，分配不同的权重进行加权求和，使二者对梯度的影响一致，避免梯度变化倾向于单个损失函数，从而使模型对数据分布的大小和位置等特征都具备学习能力。参考熵值法根据各评价指标的影响进而确定权重的原理，分别对训练过程中均方误差和皮尔逊距离损失值的变化进行观察，通过变化情况分配权重，损失变化小的分配较低的权重，损失变化大的分配较大的权重。由于二者变化程度相当，因此设置权重系数λ1和λ2均为1。采用梯度下降法使该损失函数取最小值时，可使网络输出和标签之间的误差变大，梯度变化更明显，保证网络在梯度下降过程中可跳出局部最优，从而提高低频补偿精度。

本文的结合改进CNN和双约束条件下损失函数的地震数据低频补偿方法的实现步骤如下：

(1)使用高通滤波器滤除低频成分以建立单道地震记录训练样本集；

(2)为解决梯度消失导致低频欠补偿，在深层CNN中加入残差块和BN层构建网络模型；

(3)为提高网络的收敛性能，将样本集进行归一化后输入构建的网络模型；

(4)在双约束条件下进行训练，使梯度变化更明显从而网络跳出局部最优，提高补偿精度；

(5)训练完成后得到可以实现地震数据高精度补偿的网络模型；

(6)将合成地震记录和实际叠前地震记录输入到网络模型，验证低频成分的补偿效果及对中、高频信息的保护程度。

2 地震数据低频补偿实验

为验证本文方法对地震数据低频补偿的效果，对合成地震数据和中国西部X地区实际叠前地震数据进行低频补偿，并分别与基于CNN低频补偿方法(方法Ⅰ)、反褶积结合宽带俞式低通滤波器的低频补偿方法(方法Ⅱ)进行对比。

2.1 仿真实验及结果分析

为验证方法的可行性和有效性，对合成地震数据进行了仿真实验并对结果进行分析。由于实际地震数据低频成分的缺失，无法作为标签数据，因此选取多个不同类型的合成地震炮记录共15000道，每道截取750个样点作为标签。根据X地区实际叠前地震数据低频缺失特点，用高通滤波器滤除10Hz以下低频后作为网络输入。使用改进的CNN这种“端到端”网络架构提取地震记录幅值特征，并考虑时频分布，逐道进行滤波和补偿，则网络更注重地震数据的细节信息。网络训练过程中将批大小设置为50，初始学习率设置为10-4，训练迭代次数为2000，每训练200次学习率缩小10倍。这样自动调整学习率，可以保证稳定训练的前提下，达到合理的训练效率，并减少训练时间。训练结束后，对合成地震数据进行处理，通过对比低频补偿前、后的时域波形、频谱曲线、子波波形和地震剖面验证补偿的有效性和准确性。

首先，验证加入残差块对提高网络特征提取能力的有效性。图3为加入残差块前、后损失函数随迭代次数的变化曲线，可以看出，加入残差后损失函数值下降更快，表明网络对细微变化的特征提取能力更强，从而提高了训练效率。

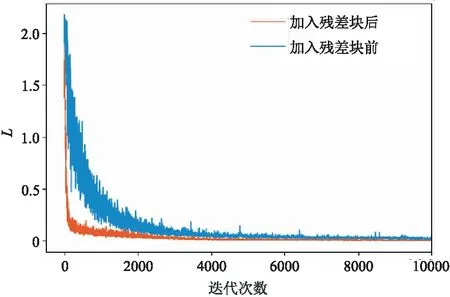
图3 加入残差块前、后损失函数变化曲线对比

然后，在网络加入残差块后，对损失函数改进前、后的低频补偿结果进行对比。图4为迭代次数为500时使用双约束损失函数与仅使用MSE作为损失函数的低频补偿时域波形对比，可以明显看出，使用改进后损失函数训练得到的网络模型低频补偿后的地震记录(图4b)与原始地震记录之间的误差更小，相似度更高，表明低频补偿精度更高。

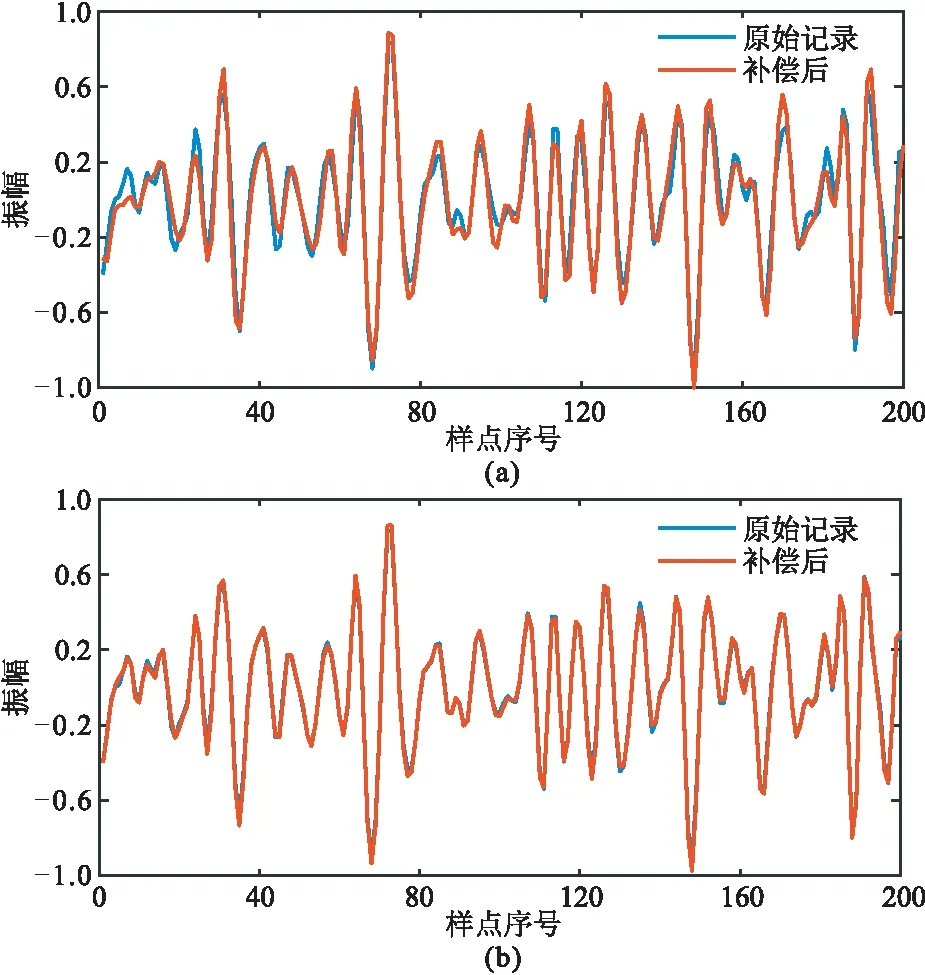
图4 损失函数改进前(a)、后(b)单道地震记录低频补偿结果的波形对比

最后，分别与方法Ⅰ和方法Ⅱ的低频补偿结果进行对比，如图5和表1所示。本文方法处理后的地震记录与原始地震记录之间的MSE和平均绝对误差(MAE)都最小，补偿后地震记录波形主瓣振幅下降且旁瓣振荡幅度减小。由低频补偿前、后频谱曲线(图6)可以明显看出，三种方法都可以对低频成分进行一定的补偿，但本文方法处理后，低频补偿的精度更高，即在补偿低频成分的同时不会损伤中、高频信息，从而保证了补偿后的有效信号中不增加噪声干扰。利用基于经验模态分解的子波提取方法[24]提取低频补偿前、后的子波波形(图7)，对比可见，低频补偿处理后，子波主瓣幅度上升，旁瓣振荡幅度减小，且本文方法低频补偿处理后的子波与原始子波形态最接近。

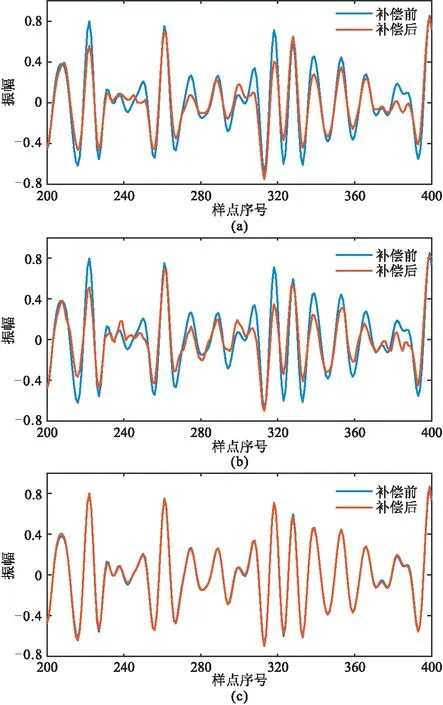
图5 合成数据三种方法低频补偿前、后波形对比

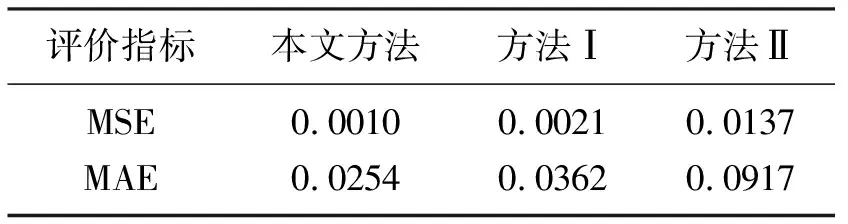
表1 合成数据三种方法补偿结果时域准确性对比

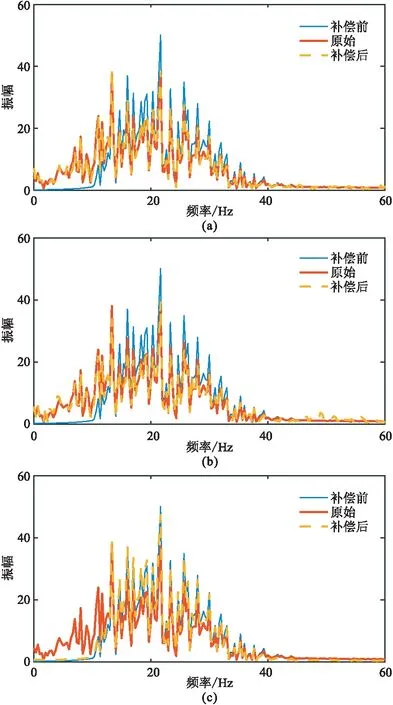
图6 合成数据三种方法低频补偿前、后频谱对比

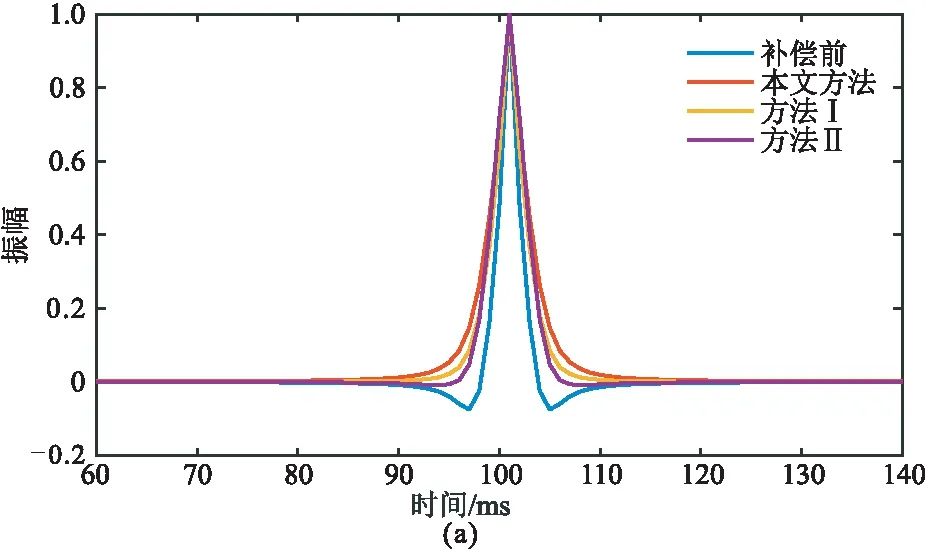
图7 合成数据三种方法低频补偿前、后子波波形对比

地震数据低频信号反映地质体整体包络，中频信号反映地质体内部的基本形态，高频信号反映地质体构造细节[25]。图8a为原始合成地震剖面，图8b为经过10Hz高通滤波后的结果。利用本文方法、方法Ⅰ和方法Ⅱ对图8b数据进行低频补偿，结果如图9所示，可见，本文方法能在不损失有效信号的前提下，使补偿后的剖面同相轴能量增强(图9a红框和黄框所示)。三种方法低频补偿结果与原始合成数据的差值剖面如图10所示，与方法Ⅰ(图10b)和方法Ⅱ(图10c)相比，本文方法补偿的低频成分误差更小(图10a)，有效低频信号能量得到增强，同时地层细节信息也得到较好的保留。利用结构相似度(SSIM)和整体MSE作为定量评价指标(表2)，与方法Ⅰ和方法Ⅱ相比，本文方法处理结果的SSIM分别高出1.1%和2.4%，MSE分别低95.9%和87.7%，从整体差异和结构两个方面都说明了与原始地震剖面更具相似性。上述分析表明，本文方法更准确、更优越。

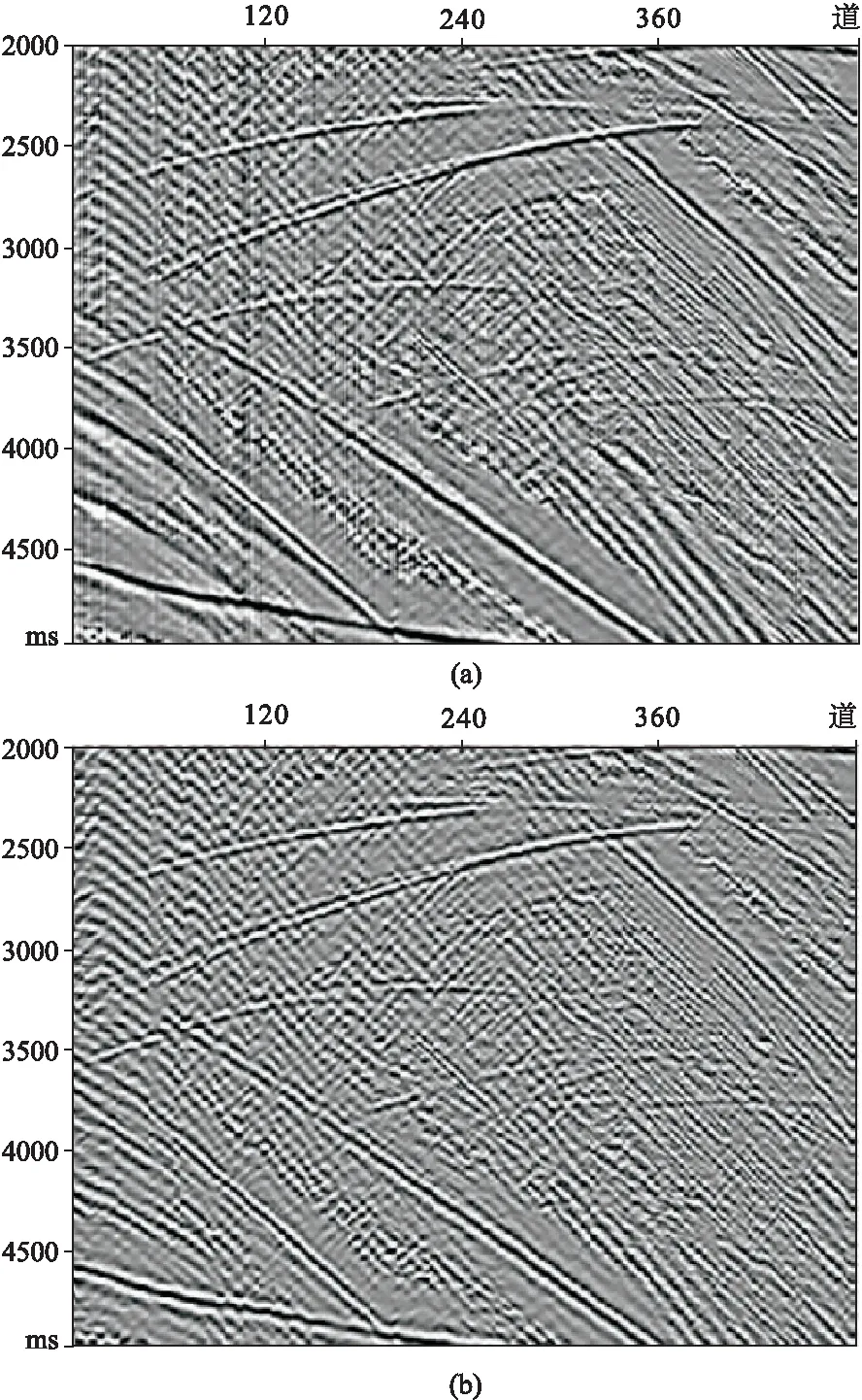
图8 合成数据地震剖面(a)及其高通滤波结果(b)

图9 合成数据三种方法低频补偿结果对比

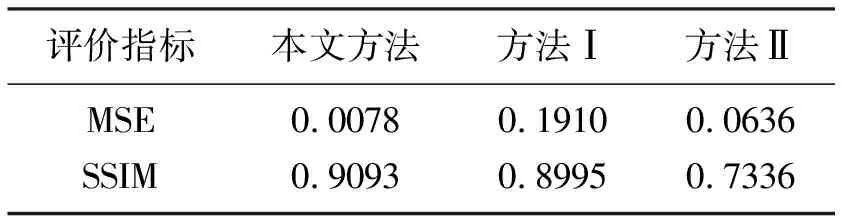
表2 合成数据三种方法补偿结果统计

图10 合成数据三种方法低频补偿结果与原始合成数据的差值剖面对比

2.2 实际数据处理及结果分析

对比X地区本文方法低频补偿前、后单道地震记录的时域波形(图11a)可以看出，低频补偿后波形的空间位置并未发生明显变化，且波形振荡幅度减小；对比低频补偿前、后频谱曲线(图11b)可以看出，低频成分得到了一定的补偿，且中、高频成分基本不变保持；提取补偿前、后的地震子波(图11c)，可见，低频补偿后子波主瓣幅度上升，旁瓣减少且振荡幅度减小。图12为低频补偿前、后的地震道集及差值，可见，低频补偿后丰富了同相轴信息，且同相轴更细、更清晰、更连续(图12b红框和黄框所示)，表明地震数据的低频能量得到有效提高，能够更准确地反映地层结构。差值道集的能量强度表明，补偿后，丰富了有效低频信号，提高了整体分辨率，说明本文方法能够有效且准确地补偿实际地震数据的低频信息。

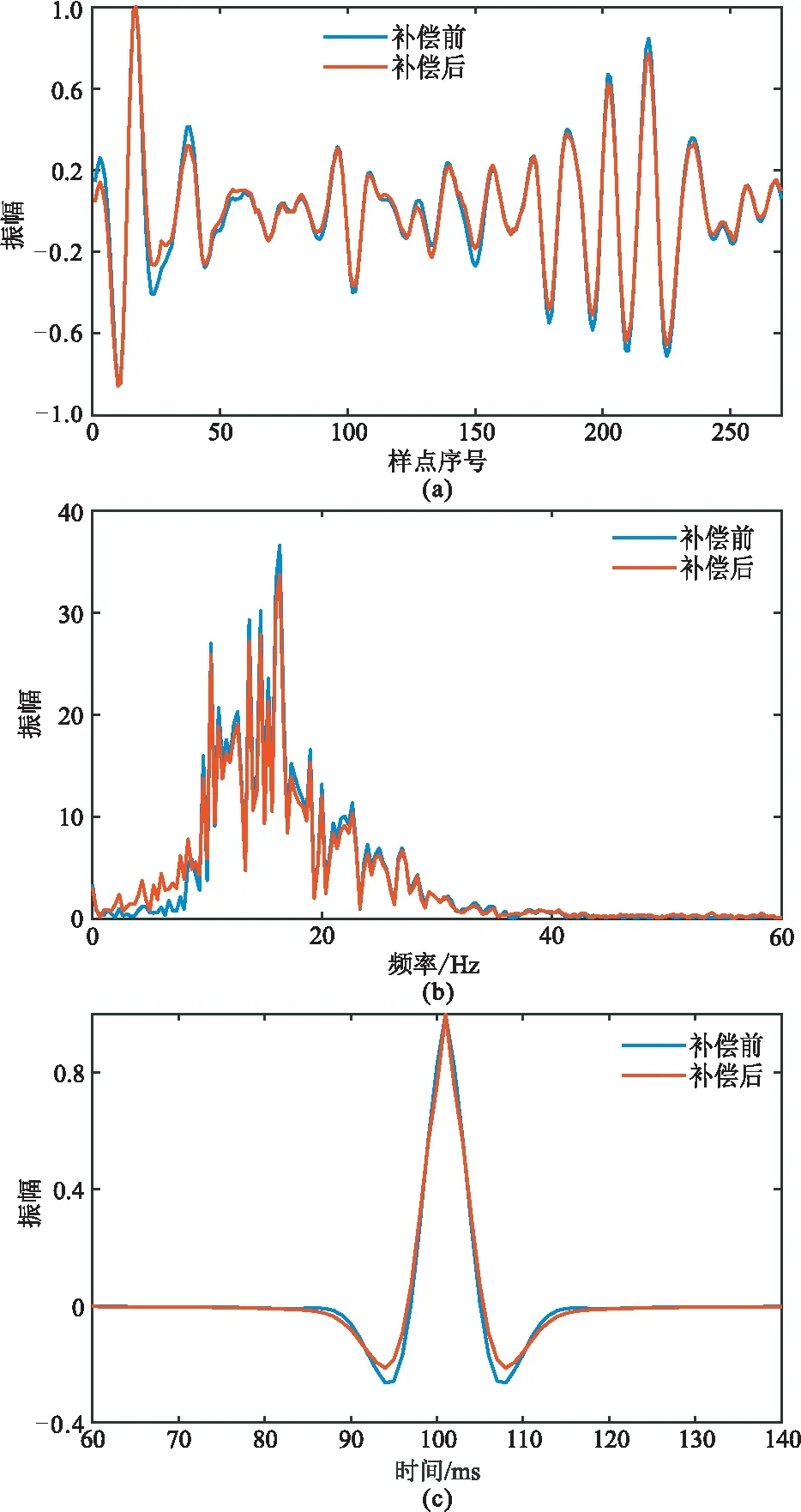
图11 实际地震数据本文方法低频补偿前、后对比

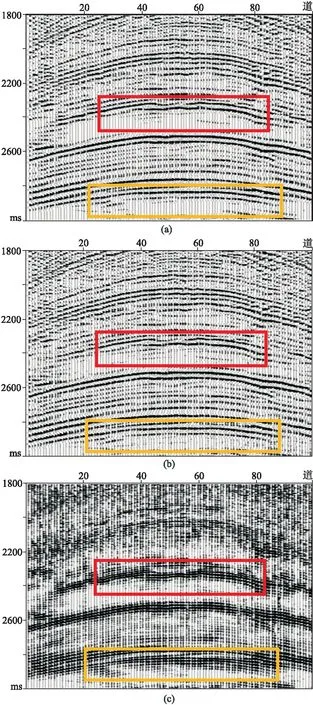
图12 实际地震道集本文方法低频补偿结果

3 结论

本文提出一种结合改进CNN和双约束损失函数的叠前地震数据低频补偿方法。首先，在CNN中引入残差块和批归一化层，解决了增加网络层数提取高层次特征时出现的梯度消失问题，使网络对细微变化更敏感，提高了网络特征提取能力和收敛速度。其次，利用均方误差和皮尔逊距离建立双约束条件下的损失函数，提升了网络输出和标签之间的差距，使梯度变化更明显，保证梯度下降过程中跳出局部最优，网络模型得到进一步优化，解决了均方误差损失函数数量级较小导致网络过早收敛的问题，提高了低频补偿精度。合成地震数据和中国西部地区实际叠前地震数据的处理结果都验证了本文方法的有效性和准确性。与基于CNN的低频补偿方法及反褶积结合宽带俞式低通滤波器的低频补偿方法相比，本文方法的补偿精度更高，具有一定的实际应用价值。