侵彻引信用磁电传感器的输出特性仿真分析

何瑶，段雨涵，隋丽，张美云

（1.北京理工大学 机电工程与控制国家级重点实验室，北京 100081；2.西北工业集团有限公司，西安 710043）

在现代战争中，世界各国为了提高毁伤型武器在战斗中的生存能力，一般采取将其地下深埋或增强防护结构等措施。在这种情形下，出现了大量具有坚固结构的硬目标。这些硬目标主要分为深层厚目标和多层硬目标2 类，其中，地下机库、洞穴等是典型的深层目标，舰船、多层建筑物等是典型的多层硬目标[1-3]。统计结果表明，同等化学当量的装药在硬目标内部的最佳位置处起爆与在其表层起爆相比，能量耦合效率可以提高20～50 倍不等[4]，控制战斗部在深入硬目标内部后再起爆是实现高效毁伤的关键。

侵彻弹药通常具有精确制导的能力，使用具有延时起爆功能的引信，可以控制战斗部在进入目标内部后的适当时机发出起爆控制信号，从而对目标总体结构以及结构内部的有生力量进行高效毁伤[5-7]。使引信设计满足相应战术指标与技术指标的要求是侵彻引信研制工作的主要任务之一，在研制过程中，很难全面考虑到打击目标的复杂性、多变性[8]。硬目标侵彻引信对炸点的精准控制[9-12]是侵彻弹药实现预期毁伤效果的关键，国内一些研究单位已经对侵彻引信的炸点控制方法进行了研究[13-16]。

侵彻引信要想实现精准的炸点控制，需要获取弹丸在侵彻靶板过程中的目标信号[17]，利用高g值传感器或加速度阈值开关作为敏感元件是获取弹丸侵彻加速度信号的主要手段[18-19]。识别目标信号的难易程度对后续信号处理的难度有很大影响[20]。目前，侵彻引信用高g值传感器主要有压电式加速度传感器[21-22]和压阻式加速度传感器[23-26]。这2 类加速度传感器都能够用于弹体长度较短的弹丸，但是当弹体增长、弹速增加时，传统的侵彻引信用压电式或压阻式加速度传感器在测量过程中会出现零漂、加速度信号混叠粘连严重等问题，识别弹丸穿层信号的难度将会增大，基于低通滤波的信号处理方法不再可行。西安机电信息技术研究所的张海涛等[27]通过对压阻式加速度传感器进行二次封装的机械滤波方法提高了传感器振动模型的阻尼比，从而达到缩短传感器动态指标中的稳定信号建立时间、降低侵彻过程中加速度信号混叠现象的目的。西安机电信息技术研究所的董灵飞等[28]提出了一种基于应力波衰减材料的目标层特征凸现方法，使用应力波衰减材料加快应力波在弹内传播时的衰减速度，使应力波在弹体内传播的时间小于弹体在两层靶板之间的飞行时间，从而避免应力波沿着弹体多次重复混叠，造成侵彻加速度的层间粘连。实验表明，采用缓冲措施后，测得的侵彻冲击加速度特征更加明显。然而，上述这些方法的本质还是基于滤波原理，仅是把获取信号后进行的滤波改为在获取信号前进行，并没有从根本上解决穿层信号混叠的问题。

基于上述情况，北京理工大学研制了一种对穿层信号[29]敏感的侵彻引信用磁电式速度传感器，它可以在一定程度上解决信号粘连混叠严重、难识别的问题。该传感器的输出特性受多种结构参数影响，因此在设计过程中难以预知其在不同侵彻环境下的输出，这类磁电传感器设计方面的相关研究目前未见报道。本文以侵彻引信用磁电式速度传感器为研究对象，基于这种磁电传感器的结构原理，建立了联合仿真模型，可以利用该模型模拟不同侵彻环境下的传感器输出情况，从而实现指导侵彻引信用磁电传感器结构设计的目的。

1 磁电传感器工作原理

侵彻引信用磁电传感器是能够获取弹丸穿层信息的惯性传感器，传感器的结构如图1 所示。内部由惯性系统、支撑结构和转换元件组成，其中转换元件包括磁铁和线圈。磁铁也是惯性系统的质量块，其底面由弹簧支撑，顶面是骨架，骨架和限位结构决定了磁铁的最大行程。当侵彻弹丸碰击目标产生冲击过载时，磁铁因惯性与线圈产生相对运动而产生感应电动势，感应电动势的大小和磁铁及线圈之间相对运动速度成正相关。

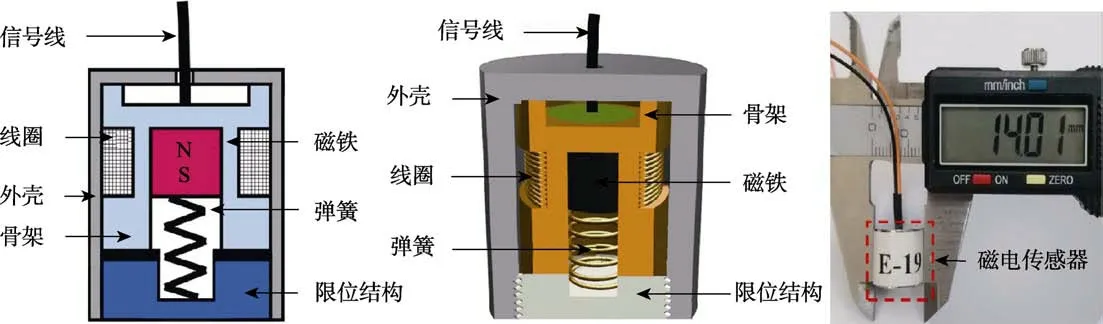
图1 侵彻引信用磁电传感器结构Fig.1 Structure diagram of magnetoelectric sensor for penetration fuze

2 磁电传感器联合仿真分析

根据侵彻引信用磁电传感器的结构原理，建立联合仿真模型，该模型分为2 部分：

1）磁电传感器惯性系统的力学仿真模型，以侵彻过载作为模型输入，获得磁铁在侵彻过程中的速度及位移变化情况。

2）磁电传感器转换元件的磁电仿真模型，以力学仿真模型获得的磁铁运动速度或位移作为模型输入，通过磁电仿真得到传感器的输出信号。

2.1 惯性系统的力学仿真方法及步骤

2.1.1 模型建立

利用Automatic Dynamic Analysis of Mechanical Systems（ADAMS）软件建立如图2 所示的磁电传感器惯性系统的力学仿真模型，将战斗部在穿靶过程中的过载信息作为该模型的仿真激励，通过仿真得到动力学响应，即质量块（磁铁）的运动位移。该模型包括上挡板、磁铁（质量块）、弹簧结构、底座限位结构4 部分，其中，磁铁的质量和弹簧的刚度、预压量等参数对仿真结果的影响较大。上挡板在力学仿真过程中仅起到给弹簧结构提供初始抗力的作用，底座限位结构起到支撑弹簧质量系统并限制磁铁行程的作用，该力学仿真模型中，磁铁的最大行程为3 mm。

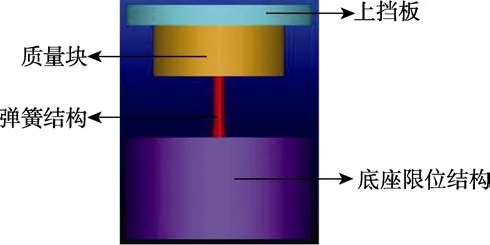
图2 磁电传感器惯性系统仿真模型Fig.2 Simulation model of magnetoelectric sensor inertial system

2.1.2 参数设置

设置模型中各部分结构的材料参数，定义质量块、上挡板、底座限位结构的密度、杨氏模量、泊松比，定义弹簧结构的刚度、阻尼、原长、预压量。本文建立的力学模型中的部分结构参数见表1。

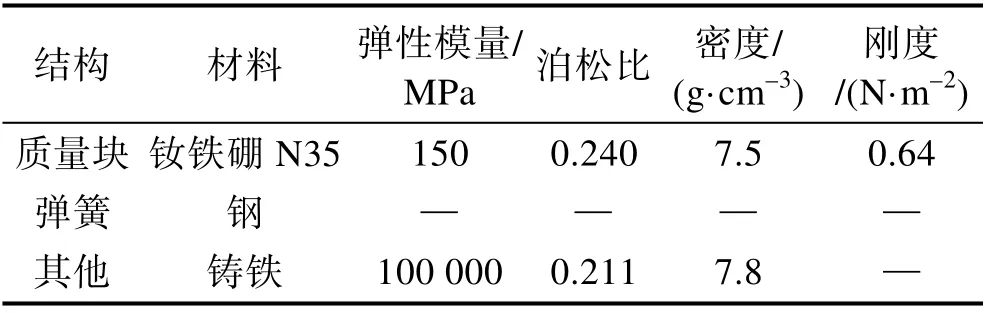
表1 结构参数Tab.1 Structural parameter

由于上挡板的几何参数对力学模型的仿真结果不造成影响，为了减少ADAMS 软件的仿真计算量，上挡板的几何结构应当在允许范围内越小越好，为了防止仿真出现自穿透现象，该结构的厚度不应过薄。综合考虑以上因素，设置上挡板为半径5 mm、高度1 mm 的圆柱体。

ADAMS 利用碰撞函数的理论计算公式（1）对碰撞过程进行仿真[30]。

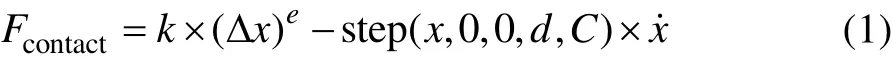
式中：Fcontact为2 个物体间接触力；k为刚度系数；Δx为碰撞物体的变形；e为碰撞指数；d为侵入深度；C为最大阻尼系数；step 函数为阶跃函数，用于表征过渡过程，step 函数的5 个参数分别表示自变量以及自变量和函数的初始值、终值。其中，刚度系数k越大，2 个物体之间的穿透量越小；碰撞指数e越大，2 个物体之间的穿透量越大；最大阻尼系数C越大，碰撞力曲线越趋于平滑。

物体的碰撞是一个极其复杂的力学过程，对于旋转物体之间的碰撞而言，仿真模型的刚度系数k可以根据式（2）确定。

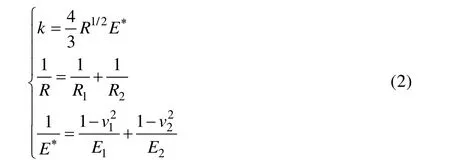
式中：R1、R2分别是2 个碰撞物体的半径；v1、v2分别是2 个碰撞物体的泊松比；E1、E2分别是2 个物体的弹性模量。

在上挡板与质量块之间设置接触1，在质量块与底座限位机构之间设置接触2，使得质量块在惯性力、重力和弹簧力的合力作用下在上挡板与底座限位机构之间上下运动。分别设置2 个接触的碰撞参数，包括刚度系数k、碰撞指数e、最大阻尼系数C和切入深度。根据式（2），通过计算对2 个碰撞过程的碰撞参数进行设置，见表2。

表2 碰撞参数Tab.2 Collision parameter

2.1.3 仿真结果

以图3 所示的半周期正弦信号为例，其中，信号的脉宽为200 μs，幅值为10 000g。将该信号作为侵彻过载，转换成力载荷，为惯性系统的力学仿真过程提供力学输入，通过仿真得到如图4 所示的磁铁动力学响应。磁铁在惯性力、重力、弹簧力的合力作用下，由初始位置向下运动，速度方向为正，呈现先快速增大、再缓慢减小的趋势。在360 μs 左右，磁铁与底座限位结构发生碰撞，此时磁铁速度迅速降为0。随后磁铁在弹簧力作用下向上运动，速度缓慢增大，速度方向为负。

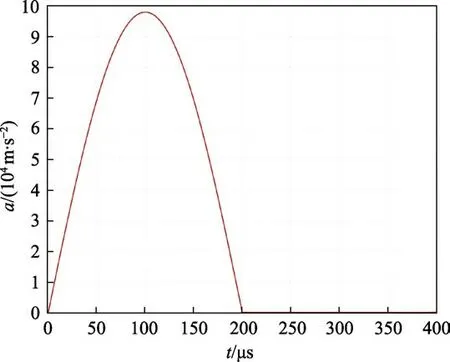
图3 侵彻过载（半周期正弦信号）Fig.3 Penetration overload (half period sinusoidal signal)

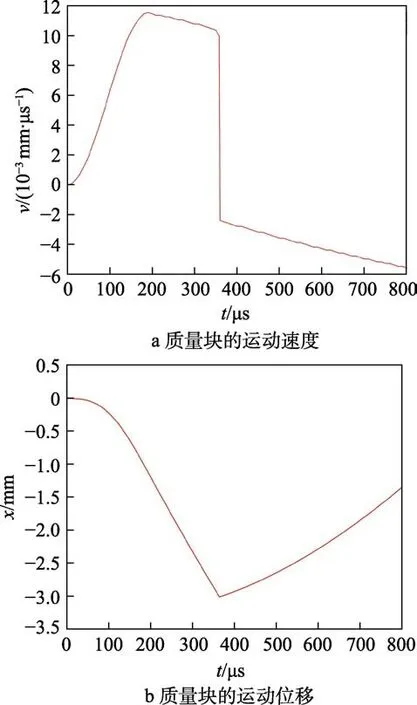
图4 质量块（磁铁）的动力学响应Fig.4 Dynamic response of mass block (magnet)

2.2 转换元件的磁电仿真方法及步骤

2.2.1 模型建立

在COMSOL 软件中建立传感器机电转换元件的磁电仿真模型。由于该结构具有旋转体的特点，所以可以通过建立1/2 的剖面二维模型对整体进行研究。仿真结果后处理时，利用几何的对称性和磁场的反对称性，还原整体的磁场分布，以实现简化运算的目的。建立模型时，使用“形成装配体”功能来确定几何，此功能假设所有对象都不相交，并在对象之间的接触边界处自动创建“一致对”，“一致对”用于在“磁场”接口中定义“对连续性”的边界条件，以确保场在不一致的网格中是连续的。将2.1 节中力学仿真获得的磁铁运动位移作为该模型的力学输入，模拟磁铁在空气域中的运动，仿真得到线圈的感应电压，即磁电传感器的输出信号，磁电仿真模型的结构如图5 所示。

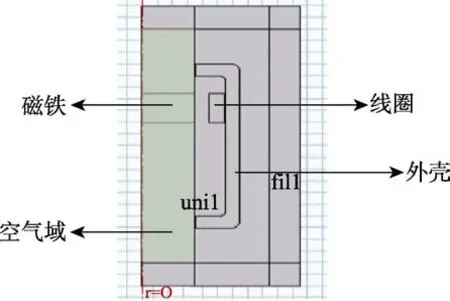
图5 磁电传感器转换元件仿真模型Fig.5 Simulation model of magnetoelectric transducer

该模型包括磁铁（质量块）、线圈、外壳和空气域4 部分，磁铁置于空气域中，磁铁在初始位置处与线圈等高，线圈位置固定。用矩形表示磁铁和多匝线圈模型，磁铁和线圈没有使用圆角，这会使网格更简单，求解规模也较小。虽然尖角会将局部奇异性引入磁场，但是在机电转换元件的磁电仿真过程中，无需担心这个问题，因为仿真的求解目标仅是线圈中的感应电压，此电压是通过域上的场积分来计算的，对场中的奇异性极不敏感。

2.2.2 参数设置

磁铁的运动过程反映了电磁感应现象，即线圈因磁通量变化而产生感应电动势及感应电流的现象。由于物理场中有电流产生，所以要通过AC/DC 模块下的“磁场（mf）”接口进行仿真分析。对物理场进行设置，定义轴对称、磁绝缘、初始值和安培定律，磁化模型选择“剩余磁通密度”，回复磁导率选择“来自材料”。设置模型的材料参数，定义磁铁的质量、剩余磁通密度的大小及方向等。设置线圈参数，导线模型选择“均匀多匝”，线圈激励选择“电流”，并定义线圈电流为0，设置线圈匝数、导线电导率以及圆导线直径。

采用四边形网格和自由三角形网格进行网格划分，首先规定磁铁上下空气域4 条边上的节点数，然后通过边映射的方法在空气域中划分出正四边形网格，接着选中剩余域，利用物理场自动划分自由三角形网格，最后手动调整网格的疏密程度。一般来说，磁场强度较大或者需要单独分析的部分网格要进行细化处理。设置动网格参数，在空气域中设置动网格来描述磁铁的运动位移，限制磁铁在r轴方向上的位移为0，通过插值函数确定磁铁网格在z轴方向上的位移。当网格在移动过程中发生过度撕扯或翻转，导致网格质量低于预设的阈值时，求解器不收敛，此时需要使用自动重新划分网格功能。

2.2.3 仿真结果

本文使用2 个步骤对转换元件模型进行求解。首先，通过磁场的稳态分析计算出磁铁在起始位置处产生的磁场，为后续磁场和动网格的瞬态分析提供初始条件。最后，通过瞬态分析得到所需的磁电传感器仿真输出信号。将图4 所示的磁铁仿真位移作为转换元件磁电仿真模型的输入，可以得到如图6 所示的传感器输出信号。

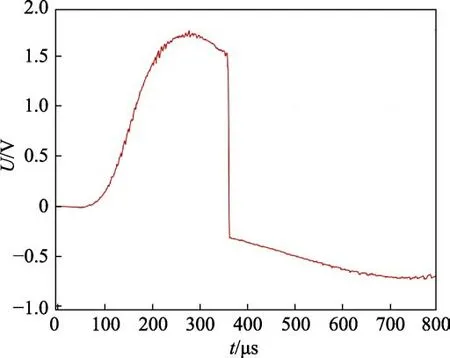
图6 磁电传感器仿真输出信号Fig.6 Simulation output signal of magnetoelectric sensor

将图4 所示的磁铁运动位移与图6 所示的传感器输出进行对比，可以看出，当磁铁向下运动时，磁铁产生磁场切割线圈，穿过线圈的磁通量不断地发生变化，线圈产生方向为正的感应电动势，传感器的输出信号为正。在大约360 μs 时刻，磁铁与底座限位结构发生碰撞，速度降为0，此时线圈中的感应电动势迅速下降到0。随后，在弹簧力作用下，磁铁向上运动，线圈中产生负电动势，传感器输出负信号。

2.3 正确性验证

本文利用落锤试验验证联合仿真模型的正确性，试验装置如图7 所示。将3 层套靶固定于试验台体上，由牵引机构将试验台体提升后突然释放，试验台体与承载台体撞击，获得过载信号和磁电传感器输出信号。将该过载信号作为联合仿真模型的初始激励，仿真得到传感器的输出信号。落锤试验得到的实测过载信号如图8 所示。

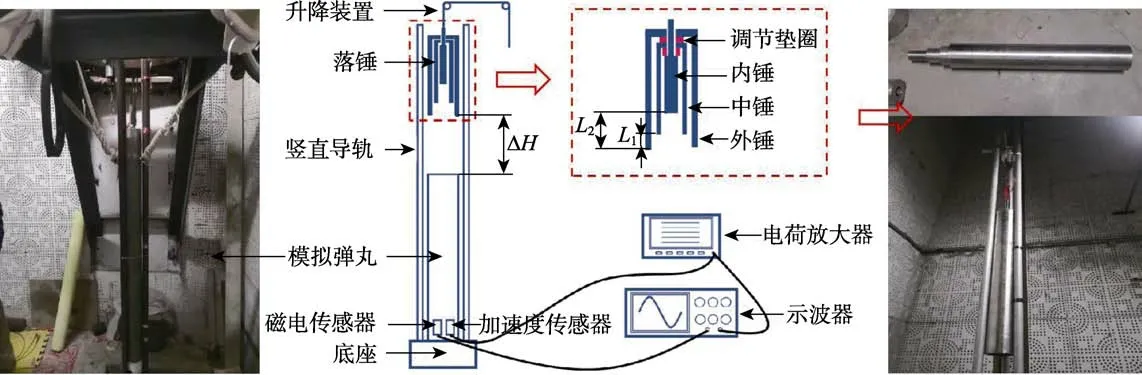
图7 落锤试验原理Fig.7 Principle diagram of drop hammer test

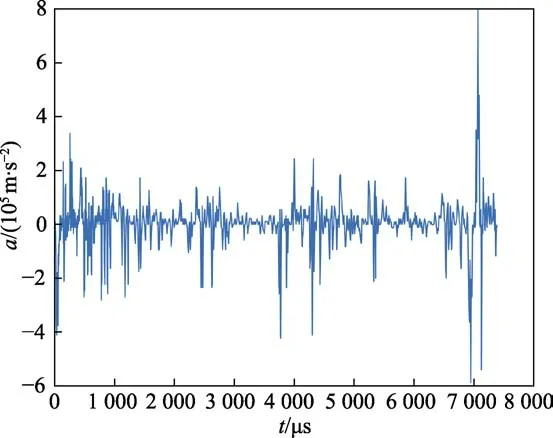
图8 落锤试验实测过载曲线Fig.8 Measured overload curve of drop hammer test

落锤试验得到的磁电传感器实测输出和通过本文建立的联合仿真模型得到的传感器仿真输出如图9所示。对比仿真与实测得到的穿靶时间与穿靶时的电压值，结果见表3。

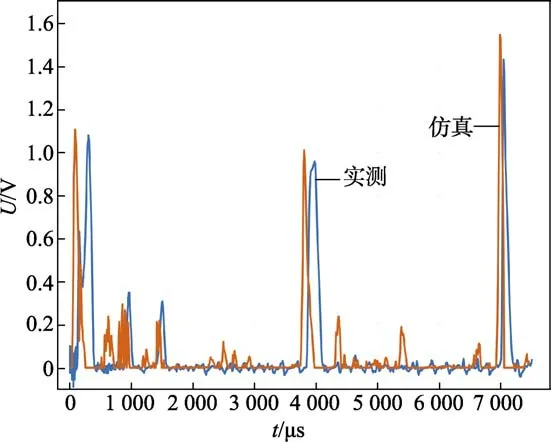
图9 磁电传感器输出Fig.9 Magnetoelectric sensor output

表3 传感器实测输出与仿真输出对比Tab.3 Comparison table of measured output and simulation output of sensor

由于实际的磁电传感器本身存在滤波电路等处理电路，所以穿靶信号波峰出现的时间相对滞后，且穿靶时刻的电压值会在一定程度上小于仿真得到的电压值。仿真结果表明，弹丸侵彻首层靶时，穿靶时间的绝对误差为184 μs，电压值的相对误差为4.1%；穿过第二层靶时穿靶时间的绝对误差为170 μs，电压值的相对误差为5.5%；穿过第三层靶时穿靶时间的绝对误差为60 μs，电压值的相对误差为8.1%。

仿真穿靶时间的平均绝对误差约为138 μs，穿靶时刻的仿真电压值的平均相对误差约为5.9%。虽然仿真数据与实测数据之间由于随机误差不可避免地存在一定的差异，但是仿真信号与实测信号的变化趋势一致，且仿真误差均在可控范围内，仿真结果不影响后续目标识别与起爆控制功能的实现。

综上所述，本文建立的联合仿真模型具有正确性和合理性，该研究分析方法具有可行性，可以利用该模型来指导侵彻引信用磁电传感器的设计。

3 结构参数对磁电传感器输出特性的影响

侵彻引信用磁电传感器的输出特性受力学仿真模型和磁电仿真模型2 部分影响。其中，惯性系统的力学仿真输出（即磁铁的运动位移）取决于磁铁质量m、弹簧刚度k、弹簧阻尼C、限位行程d等结构参数，在力学仿真输出一定的前提条件下，转换元件的磁电仿真输出主要取决于线圈参数。

3.1 仿真条件

在本次研究中，不改变力学仿真模型的结构参数，仅改变磁电仿真模型中的线圈参数，即在给定侵彻过载的条件下，磁电传感器惯性系统的力学输出是一定的，仅有传感器转换元件的输出特性发生改变。以弹丸侵彻单层厚靶（靶厚2 m，靶材为C30 混凝土，弹长1.6 m，弹速为1 200 m/s）时的侵彻过载作为联合仿真模型的初始激励，通过惯性系统的力学仿真可以得到磁铁的运动位移，如图10 所示。将该位移作为磁电模型的仿真输入，分别改变线圈的匝数、位置以及线圈与磁铁之间的间隙进行一系列的仿真对比与分析，各次仿真的传感器结构参数见表4。

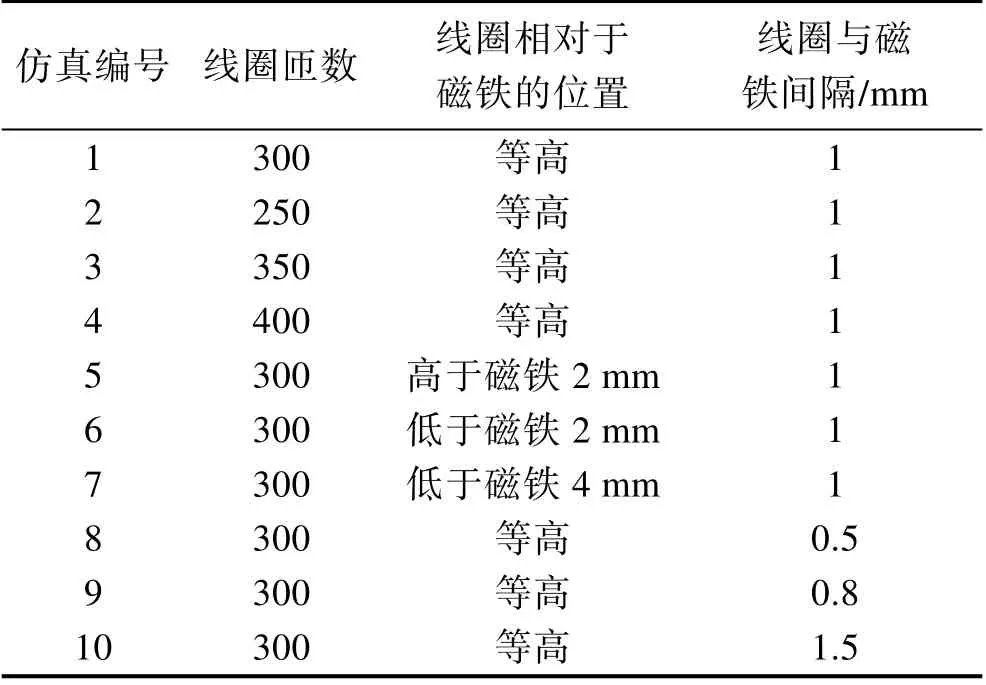
表4 传感器结构参数Tab.4 Sensor structure parameter

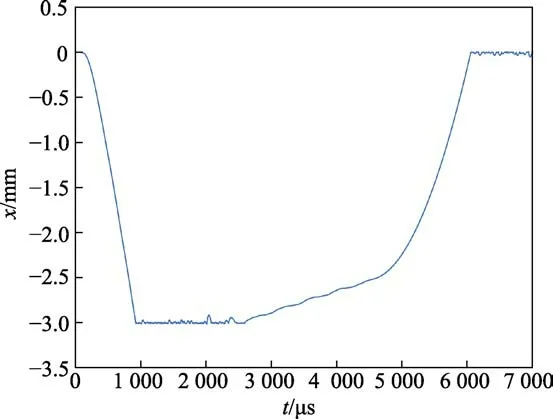
图10 磁铁的运动位移Fig.10 Motion displacement of magnet

3.2 线圈匝数对仿真结果的影响

分别进行仿真1、2、3、4，可以得到如图11 所示的磁电传感器输出信号。由图11 可知，在其他线圈参数一定时，仅改变线圈的匝数，对传感器信号中穿层信号的起始时间、结束时间以及波峰出现的时间不会造成影响。随着线圈匝数的增多，穿层信号的幅值增大，因此侵彻引信用磁电传感器中线圈的匝数不应过小。在实际应用中，可以根据所给的目标识别与起爆控制策略，设置合适的线圈匝数。

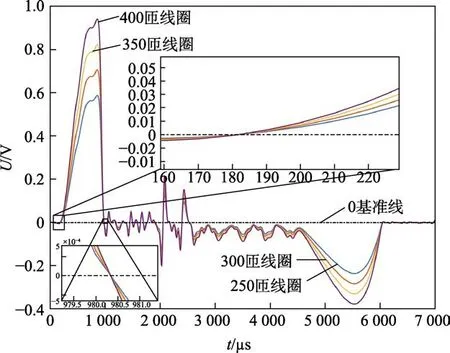
图11 不同线圈匝数时的磁电传感器仿真输出Fig.11 Simulation output of magnetoelectric sensor with different coil turns

3.3 线圈位置对仿真结果的影响

分别进行仿真1、5、6、7，可以得到如图12 所示的磁电传感器输出信号。由图12 可知，改变线圈相对于磁铁的位置，会影响穿过线圈的磁通量的正负，即对输出信号的正负造成影响。当线圈高于磁铁时，输出信号大致的趋势是先正后负；反之，当线圈低于磁铁一定距离时，输出信号大致的趋势是先负后正。在实际应用中，可根据具体需求，通过处理电路，滤去正半轴波形或负半轴波形。此外，线圈与磁铁的相对高度会影响穿层信号波峰出现的时间。从图12中可以看出，当线圈与磁铁等高以及线圈低于磁铁4 mm 时，信号的幅值都相对较大，并不是线圈与磁铁在高度上越接近时幅值越大。

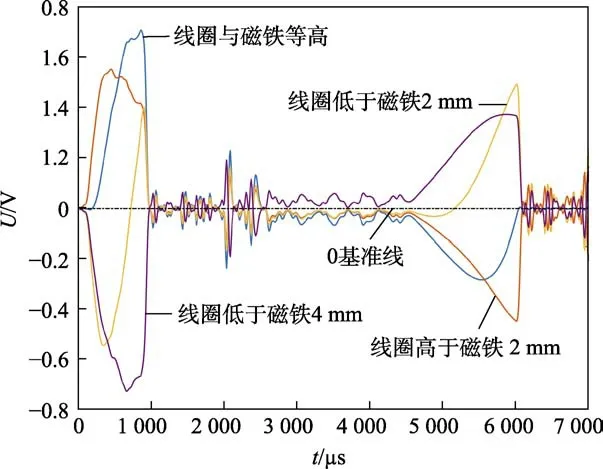
图12 不同线圈位置时的磁电传感器仿真输出Fig.12 Simulation output of magnetoelectric sensor at different coil positions

2.4 线圈与磁铁间隔对仿真结果的影响

分别进行仿真1、8、9、10，可以得到如图13所示的磁电传感器输出信号。由图13 可知，改变线圈与磁铁之间的间隔会对输出信号中穿层信号的起始时间造成影响，间隔越小，起始时间越小，但是对穿层信号的结束时间基本没有影响。线圈与磁铁之间的间隔越小，穿层信号的幅值越大。实际应用中，可以根据具体需求一定程度上减小两者之间的距离，获取电压幅值更大的输出信号。

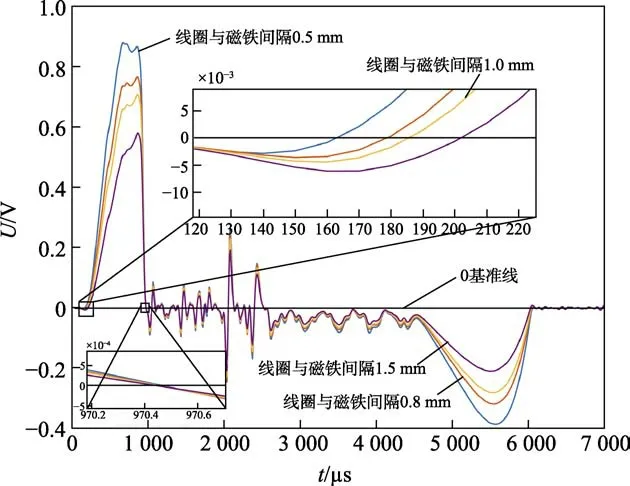
图13 改变线圈与磁铁间隔时的磁电传感器仿真输出Fig.13 Simulation output of magnetoelectric sensor with changing interval between coil and magnet

4 结论

基于侵彻引信用磁电传感器的结构原理，提出了联合仿真模型。模型验证实验表明，仿真与实测得到的磁电传感器输出信号的变化趋势一致，吻合度较高，证明了该模型的正确性与合理性。

给定侵彻过载，在不改变力学仿真模型参数的条件下，通过调整转换元件磁电仿真模型的结构参数，模拟并分析了线圈参数对磁电传感器输出特性的影响。线圈与磁铁的相对高度会影响输出信号的正负、幅值以及波峰出现的时间，线圈匝数和线圈与磁铁之间的间隔仅对信号的幅值产生影响，线圈匝数越多、与磁铁之间的间隔越小，输出信号的幅值越大。该模型可以指导磁电传感器的设计，有效降低磁电传感器的设计成本，缩短传感器的研制周期。

基于仿真得到的磁电传感器输出，通过合适的目标识别与起爆控制策略，可以获取穿层信号与起爆控制信号，为侵彻引信起爆控制系统性能的验证工作提供了新的思路，具有一定的现实意义和工程价值。