多变量时延系统的模糊控制设计

郭丙君

（华东理工大学信息学院，上海 200237）

对于多变量时延系统，可以应用多变量时延预估器进行设计，其中，对多变量时延系统的解耦控制也是一个重要的问题。首先针对多变量时延系统设计出具有静态与动态解耦的控制方法，然后应用预估控制来补偿系统的时延影响[1]，最后应用模糊控制方法来设计了控制器[2]，当然也可以进一步应用神经网络控制器或者复合智能控制器等进行设计。

1 多变量时延系统的解耦预估模糊控制

多变量时延系统解耦预估补偿控制原理如图1所示。对于一般的多重时延对象GD（s），要实现多变量时延系统在预估补偿基础上的静态及动态解耦控制，应将预估补偿控制及解耦控制有机结合起来考虑。图1中，GP（s）为解耦矩阵，使得GD（s）GP（s）成为对角矩阵；F（s）为预估补偿矩阵；GC（s）为控制器组的对角矩阵。令：

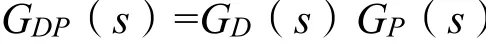
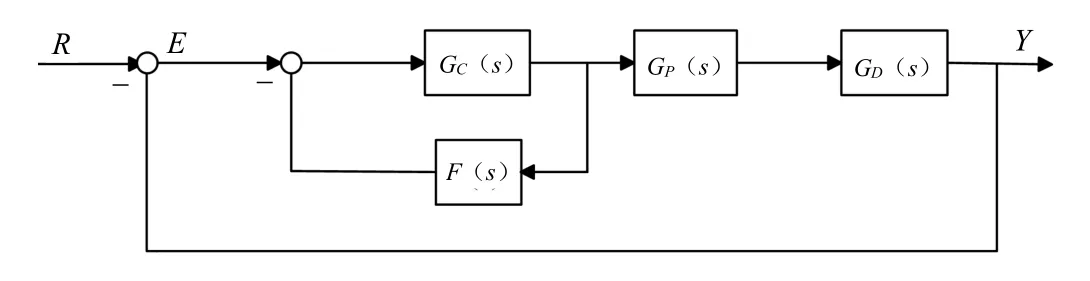
图1 多变量时延系统解耦预估补偿控制原理图

根据被控对象设计解耦矩阵GP（s），使得GDP（s）为对角矩阵，再根据GDP（s）设计预估补偿矩阵F（s），最后按照单变量系统来整定控制器GC（s）。其中，预估补偿矩阵为：

可以推导出系统的闭环传递函数为：

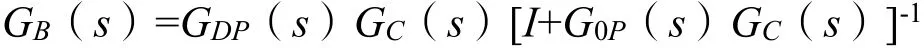
显然，该系统的闭环特征方程式中已经没有出现时延，实现了系统的预估补偿控制。

而解耦矩阵GP（s）是根据被控对象的传递函数矩阵来设计的，使得GDP（s）为对角矩阵，从而G0P（s）也是对角矩阵，由于矩阵的左乘、右乘或者求逆均是对角矩阵，该系统的闭环传递函数也是对角矩阵，从而实现了系统的静态和动态的解耦控制。应该指出，在设计解耦矩阵GP（s）时，要保证设计出的矩阵物理上的可实现性，可以在GP（s）矩阵的对角元素上适当选取相应的时延来保证解耦矩阵GP（s）可以实现。最后，在设计控制器矩阵GC（s）时，可以采取多种方案，常规的控制器是PID，为了进一步提高系统的控制性能，本次设计采用了模糊控制器。

图1中控制器矩阵GC（s）应用了模糊控制方法进行设计，是以模糊集和模糊推理为基础的。图1中的系统已经进行了解耦设计，可以对这个多变量系统应用单变量的原则分别进行各个模糊控制器的设计，这样降低了模糊控制器的设计难度。应该指出，一般的模糊控制往往存在稳态误差，通常的设计方法是引入相应的积分项，这样可以消除控制系统的稳态误差。

2 仿真实验

实验的被控对象是某单位表面式冷却器（简称表冷器）试验台，表冷器试验台是用来研究和测定表冷器热工性能的设备，被控参数为温度及湿度。在温度25℃、湿度35%附近的数学模型为：

式（2）证明了该系统湿度对温度没有耦合作用，而温度对湿度有较强的耦合作用。

其解耦矩阵为：

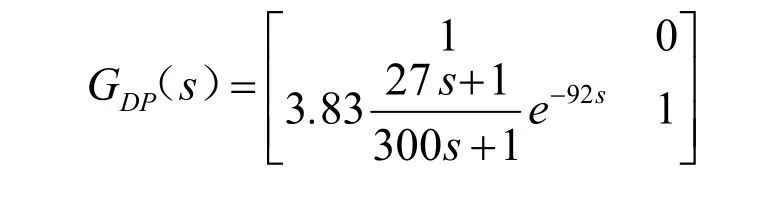
相应的预估补偿矩阵为：

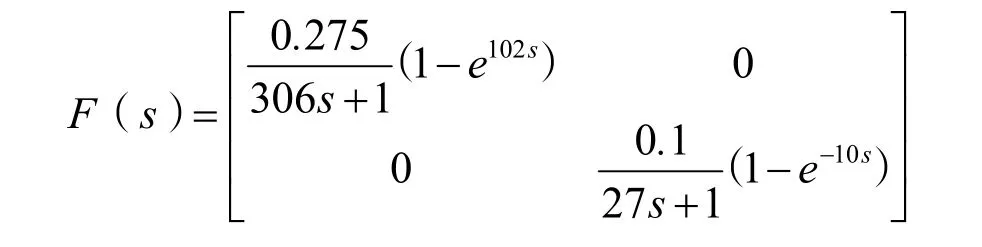
温度回路的模糊控制仿真中参数为ke=100，kd=0.01，ki=0.001，ku=1。湿度回路的模糊控制器仿真中参数为ke=30，kd=1，ki=0.1，ku=1。模糊控制器输出为：

温度的输入隶属度函数如图2所示，输出隶属度函数如图3所示。模糊控制规则是常规的25条。湿度的输入隶属度函数如图4所示，输出隶属度函数如图5所示。模糊控制规则同样是常规的25条。

图2 温度的输入隶属度函数

图3 温度的输出隶属度函数

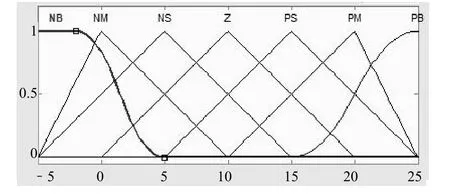
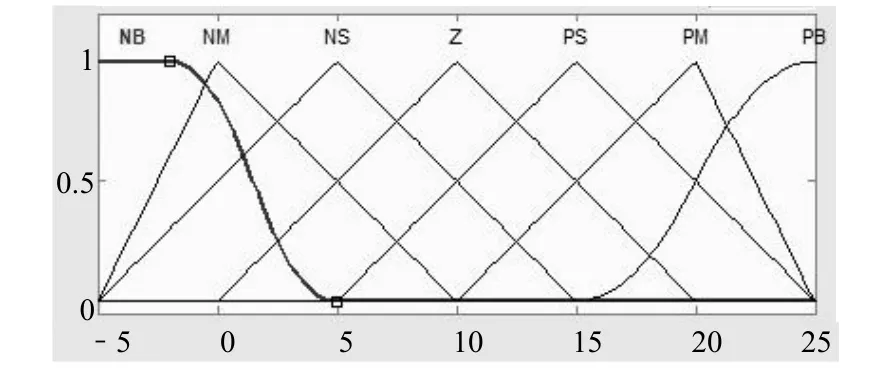
图4 湿度的输入隶属度函数

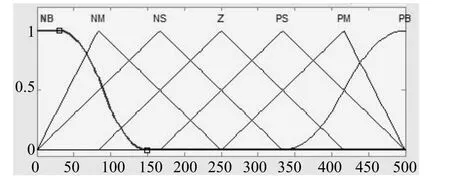
图5 湿度的输出隶属度函数

应用MATLAB/Simulink进行了仿真，仿真结果如图6所示。可见，模糊控制比预估控制具有更好的性能。为了验证模糊控制的鲁棒性，将温度回路的惯性时间常数修改为356 s，湿度回路的惯性时间常数修改为37 s，仿真结果如图7所示，模糊控制具有比较好的鲁棒性。

图6 模糊控制比较结果1

图7 模糊控制比较结果2

3 结论

对于多变量时延系统，应用解耦预估补偿基础上引入了模糊控制设计，在保证实现了系统的静态和动态的解耦控制的基础上，应用模糊控制是很方便实现的，仿真结果表明模糊控制可以取得良好的跟随性能，也具有比较好的鲁棒性。