基于E-B模型的拉苏洛面板坝应力变形分析
2022-12-08张博张楠
张博,张楠
(1.山东电力工程咨询院有限公司,山东济南250013;2.德州市生态环境监控中心,山东 德州 253076)
1 引言
面板堆石坝具有施工方便、造价低廉并且可以应对复杂地质条件等优点,已广泛地应用于高坝建设中[1]。岩土材料具有非线性、弹塑性、剪胀性以及压硬性等特点,很难获得解析解,非线性有限元方法被广泛地应用于面板堆石坝的设计分析中。
拉苏洛水利工程挡水建筑物采用混凝土面板堆石坝。坝底高程8.0 m,正常蓄水位130.0 m,相应库容10.99亿m3,死水位95.0 m,调节库容8.66亿m3,水库具有完全年调节能力。大坝坝顶高程131.5 m,河床段趾板建基高程8.0 m,最大坝高123.5 m,最大坝底宽度约402.0 m,坝轴线长378.0 m,面板分缝宽度分别为12 m(压性垂直缝)、6 m(张性水平缝),典型剖面如图1所示。采用静力有限元方法分析其蓄水前后的变形特性,并验证该坝堆石料的合理性。
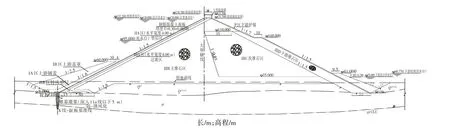
图1 大坝典型剖面
2 筑坝材料的本构模型
拉苏洛面板堆石坝垫层料、过渡料、主堆石区、下游堆石区为堆石料,采用E-B本构模型[2]。E-B本构模型为非线性弹性模型,受制于本身假设缺陷,其无法反映土石料的剪胀性、软化性及各向异性,但可以较好地反映堆石料的非线性和压硬性这2种主要性质。工程实践中,选材一般首先排除遇水软化石料;筑坝过程中使用重型机械碾压并控制其孔隙率,竣工后堆石料处于高围压状态,使得其在受剪时表现出一定的延性,剪胀消失。由于其表达式简洁,可以反映土体变形主要特点,各参数具有明确的物理意义,因此在工程实践中获得了广泛的认可,积累了丰富的经验[3]。顾淦臣[4]对原始E-B模型进行了改进,以平均主应力代替围压,以广义剪应力代替偏应力,通过多个工程监测数据的对比,更好地反映堆石坝的实际变形。
混凝土和土石料的刚度差异性较大,混凝土面板与垫层料间会产生非协调变形,因此有限元分析中应采用接触面单元模拟变形的不连续性。采用GOODMAN三维接触面单元,其上盘四节点位于面板单元上,其下盘四节点位于垫层料堆石单元上,其应力应变关系采用双曲线模拟[4,5]。
为了防止混凝土产生收缩裂缝以及简化面板受力特性,混凝土面板间及其与趾板间存在伸缩缝,分缝止水材料采用紫铜止水片。止水铜片采用GOODMAN单元模拟,其本构模型为非线性弹性模型[4,5]。
由于采用大量的分缝处理,混凝土面板和趾板为简单的拉压状态,应力应变关系可采用线弹性模型[6]。
3 三维有限元模型
为分析覆盖层对坝体变形的影响,将覆盖层与坝体主体统一建模,三维有限元模型如图2所示。沿坝轴线方向,共设定了40个计算剖面进行剖分,整个坝体结构共剖分得到总节点数16633个、总单元数14413个。
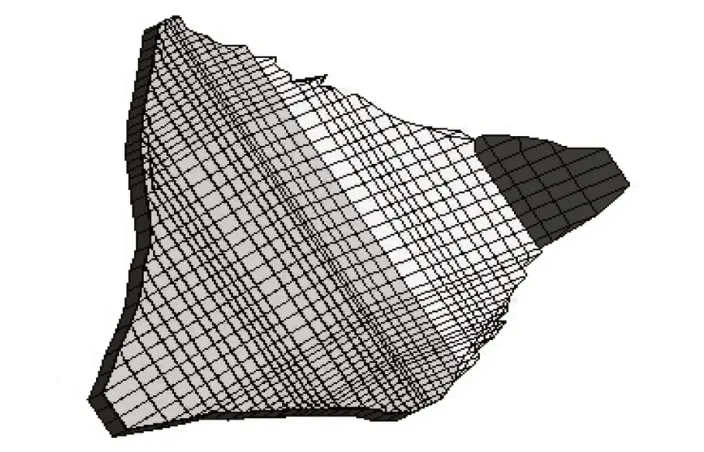
图2 坝体有限元模型
坝体施工为分层填筑,为准确得到坝体的变形需模拟其施工过程,采用增量有限元方法进行计算。按坝体施工填筑高程的先后顺序,坝体加载过程共分32级,详见表1,顺序如下:①坝体主体部分采用3~5 m一级的方式填筑,共采用31级来模拟。②面板最后一次性浇筑至坝顶,采用第32级来模拟。考虑水库蓄水过程,在模拟蓄水加载时采用逐级加载。根据水库的特征水位,蓄水过程采用3~5 m一级的方式加载,共分为3期:加载至死水位,高程为95 m;加载至正常蓄水位,高程为130 m;加载至校核洪水位,高程为132.28 m。

表1 坝体填筑分级加载过程
本文计算采用的E-B模型参数,详见表2。接触面模型参数及止水铜片模型参数同参考文献4和5。
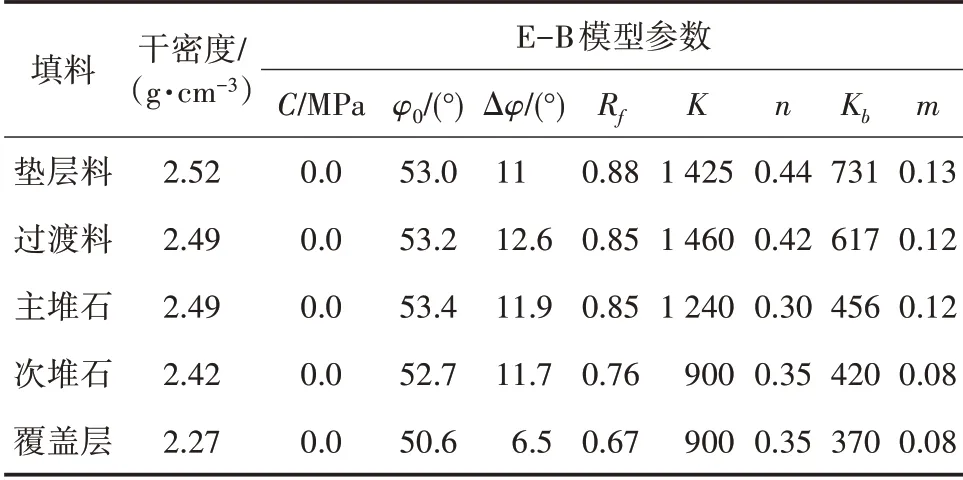
表2 坝料的E-B模型参数
4 计算成果与分析
采用三维有限元分析方法,对大坝进行应力分析,坝体变形与应力极值详见表3。
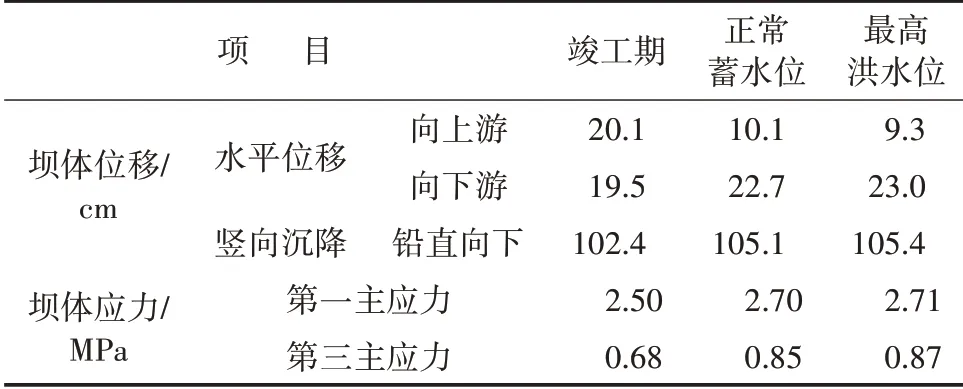
表3 三维非线性有限元计算坝体变形和应力极值
堆石体位移分布,如图3—4所示。由于泊松效应影响,上下游剖面的水平位移均指向坝坡方向;伴随着水库蓄水过程,大坝整体发生指向下游的变形,但上游堆石的变形仍指向上游坝坡,说明堆石料间依靠自重产生的咬合力和摩擦力足以抵抗水库满蓄时水平力的影响。大坝竖向位移竣工期极值为102.4 cm,位于高程80.0 m附近的主堆石区,低于坝高的1%,符合规范要求[7];蓄水过程中水荷载垂直于面板,其引起的第一主应力增量较小且使围压也相应增大,进而使应力主轴发生旋转,所以蓄水过程中竖向位移增量较小。

图3 水平位移分布
堆石体的应力分布,如图5—6所示。竣工期堆石应力由自重产生,主应力等值线与坝坡基本平行,且从坝顶向下逐渐增大,极值均位于河床坝底轴线部位;蓄水过程中,水荷载指向坝体内部,由于堆石料具有较强的非线性,加上高围压三轴试验的本构参数可一定程度反映颗粒破碎的影响,因此蓄水期大、小主应力等值线在上游堆石区都出现上抬现象,相对竣工期而言,极值有所增大且位置向上游主堆石区靠近,但坝体变形使颗粒间相互摩擦,进而耗能,使得这一影响范围有限。

图5 第一主应力分布
剪应力水平分布,如图7所示。各种工况下其应力水平值均小于1.0,未发现堆石体内剪切破坏单元,坝内各分区单元应力基本协调;满蓄期堆石料应力增加,但其最大应力水平低于竣工期极值,因为堆石料具有明显的压硬性,蓄水期堆石料围压增加,其破坏强度也相应增加,进而使得其剪应力水平下降和位置下移。
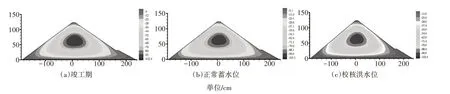
图4 竖向位移分布

图6 第三主应力分布

图7 剪应力水平分布
5 结论
(1)坝体应力变形规律可以反映出坝体堆石料的非线性和压硬性特性,表明计算过程合理准确。
(2)计算结果表明,坝体位移、应力分布规律较为合理,变形极值满足规范要求,因此筑坝材料选取合理,可以满足施工期和正常运行期的安全性要求。
