Al2O3-MgO和Al2O3-MgO-SiO2体系的热力学优化与计算

马天一，刘钰玲，高枫杨，张亮，杜勇

Al2O3-MgO和Al2O3-MgO-SiO2体系的热力学优化与计算

马天一，刘钰玲，高枫杨，张亮，杜勇

(中南大学 粉末冶金国家重点实验室，长沙 410083)

文献中Al2O3-MgO二元体系的热力学参数在外推至多元系时与实验数据存在偏差，本工作基于热力学数据的严格评估，采用CALPHAD(calculation of phase diagram)方法对该体系进行热力学重新优化，并在此基础上进一步完善Al2O3-MgO-SiO2体系的热力学描述。优化过程中，采用离子双亚点阵模型描述液相，用CEF(compound energy formalism)化合物能量模型描述固相。所得Al2O3-MgO体系和Al2O3-MgO-SiO2体系的相图热力学计算结果与绝大部分实验数据相吻合，是构建Al2O3-SiO2-MgO-CaO-Fe2O3-Na2O六元体系热力学数据库的基础，并可为大宗铝硅酸盐固废材料化设计与高值化应用提供理论依据。

Al2O3-MgO-SiO2体系；Al2O3-MgO体系；热力学优化；CALPHAD；相图计算

我国矿产资源迅速开发，冶金、化工和煤电等行业迅猛发展，产生了大量的尾矿、废石、矿渣以及赤泥和煤矸石等固体废弃物。“十三五”以来，我国大宗工业固废年产生量约35亿吨以上，固体废物中仍含有大量可利用元素，如Al2O3、SiO2、CaO、Fe2O3、MgO、Na2O等重要的氧化物组分，如此巨大的工业固废如不能得到合理的处置和利用，必将对环境和安全带来巨大隐患[1]。目前，实现大宗工业固体废物的综合利用是实现生态环境良性循环的必由之路。工业固废的综合利用常见手段包括高炉渣、粉煤灰耦合制备保温岩棉；粉煤灰、煤矸石耦合制备陶瓷纤维；煤矸石、粉煤灰耦合制备新型耐火材料；粉煤灰、污泥(尾矿)耦合制备透水砖等[2−3]，其中涉及到大量的相变转化过程。Al2O3，MgO，SiO2是煤矸石、粉煤灰等工业固废的主要组分，因此，Al2O3-MgO和Al2O3-MgO- SiO2体系的相图热力学研究对于揭示相关固废的矿相重构转化机理具有重要意义。

本工作对铝硅酸盐固废体系的相图热力学研究，主要基于CALPHAD方法[4]，建立热力学理论模型，评估热力学信息并构筑描述每个相吉布斯自由能的热力学参数，对有限的相图及热力学数据进行优化，获取覆盖全成分及温度范围的热力学描述，通过Thermo-Calc软件[5]实现相图和热力学性质图计算[6]。本工作是建立Al2O3-SiO2-MgO-CaO-Fe2O3-Na2O六元氧化物体系热力学数据库的重要基础。

HALLSTEDT[7]使用离子双亚点阵模型(Al+3, Mg+2)P(O−2)Q描述液相，对Al2O3-MgO体系进行热力学评估，计算相图与实验数据吻合较好，但对尖晶石反转度的实验数据评估不够全面，计算结果与实验数据存在一定误差。2004年JUNG等[8]采用修正的准化学模型描述液相，对Al2O3-MgO体系重新进行热力学评估，改进了尖晶石相的热力学参数，但模型中未考虑MgO在尖晶石相中的溶解度。同年，MAO等[9]对Al2O3-MgO二元系也进行了热力学评估，采用离子双亚点阵模型(Al+3,Mg+2)P(AlO2−1,O−2)Q描述液相。与此前研究者使用的离子双亚点阵模型相比，MAO等[9]采用AlO2−1代替阴离子亚点阵中的AlO1.5对液相中的Al2O3进行建模，以保证该子体系外推至含SiO2多元系时能够准确描述富SiO2端的液相溶混间隙，取得了很好的效果。此外，还对尖晶石相的热力学参数进行了改进，计算结果与实验数据吻合较好，但对尖晶石相纯Al2O3端际组元的描述与公认参数不符，无法将其应用于六元氧化物体系热力学数据库。最新的Al2O3-MgO二元系评估由ZIENERT等[10]报道，仍采用离子双亚点阵模型(Al+3,Mg+2)P(AlO1.5,O−2)Q描述液相，在拓展至多元系时与液相混溶间隙实验数据存在差异，计算结果也与Halite相固相线实验数据存在偏差，但对尖晶石相的实验数据进行了严格评估，获得了较准确的尖晶石相热力学参数。因此，有必要基于更加合理的离子双亚点阵模型以及更加准确的尖晶石相参数，对Al2O3-MgO二元系重新进行热力学评估 优化。

对于Al2O3-MgO-SiO2体系，2005年MAO[11]采用离子双亚点阵模型(Al+3,Mg+2)P(AlO2−1,O−2,SiO4−4, SiO20)Q描述液相，能够较好地描述液相混溶间隙，但Spinel固相参数并未结合新的实验数据进行优化。JUNG等[8]采用修正的准化学模型描述该体系液相，但对于混溶间隙的描述并不准确，与实验数据存在出入，急需更加精准的热力学描述。

综上，本工作将对Al2O3-MgO体系重新进行热力学评估优化，并在此基础上对Al2O3-MgO-SiO2体系的热力学描述进行改进，以解决多元氧化物体系中不同子体系之间热力学模型及参数冲突的问题。进而为构筑合理可靠的Al2O3-SiO2-MgO-CaO-Fe2O3-Na2O六元氧化物体系热力学数据库提供保障，并为大宗工业固废的综合利用冶金新工艺的开发提供理论基础。

1 实验数据评估

1.1 Al2O3-MgO体系

初步研究中，RANKING等[12]测定了MgAl2O4的熔融反应温度为1 925 ℃。ALPER等[13]通过高温淬火实验，结合光学显微镜和X射线衍射(XRD)分析，研究了氮气气氛下Al2O3-MgO体系的相图。VIECHNICKI等[14]利用塌锥技术研究了氩气气氛下Al2O3-MgO体系的固相线和液相线，并发现1 975 ℃时存在共晶反应Liquid=Corundum+Spinel。VIECHNI- CKI等[14]测定的反应温度比RANKING等[12]报道的1 925 ℃要高。RANKING等[15]以及WARTE-HBERG等[16]测定了Spinel相在空气中的熔点，分别为2 135 ℃和2 115 ℃。ALPER等[13]用光学高温计在氮气气氛中测定其熔点为2 105 ℃。在误差范围内以上实验结果均可接受，本工作采用ALPER等[13]的结果。

ZIENERT等[10]研究了该体系中的液相线和固相线，通过差热分析实验证实了Spinel相与Corundum相在1 995 ℃下的包晶反应Liquid+Corundum= Spinel。考虑到差热分析仪器误差小，本工作中热力学优化过程采纳ZIENERT等[10]的实验信息。SHIRASUKA等[17]测量了1 327～1 927 ℃之间Al2O3在Spinel中的溶解度。SEIFERT等[18]测量了1 125 ℃到1 625 ℃范围内，Al2O3在Spinel相中的溶解度。本工作评估采用RANKIN等[15]、WARTENBERG 等[16]、ALPER等[13]报道的实验数据。

1.2 Al2O3-MgO-SiO2体系

RANKIN等[15]基于实验结果构筑了Al2O3-MgO- SiO2体系的液相面投影图，并通过高温淬火实验研究了1 550 ℃以下的一系列等温截面，只发现一种三元化合物Cord，2MgO·2Al2O3·5SiO2的存在(各相名称的缩写见表1)，GREIG[19]利用淬火技术研究了该体系液相混溶间隙。随后，FOSTER[20]发现另一种三元化合物Sap，7MgO·9Al2O3·3SiO2。KEITH等[21]详细研究了涉及Sap的相平衡，通过高温淬火实验研究了Sap相的小的固溶度范围。SCHREYER等[22]全面研究了Al2O3-SiO2-MgO体系与Cord相的相平衡，结果表明Cord相具有从2MgO·2Al2O3·5SiO2到3MgO·Al2O3·6SiO2的固溶度范围，具有两种晶体结构(斜方晶和六方晶)。ARAMAKI等[23]通过高温淬火实验研究了Mul相和Corundum相之间的相区边界。SCHLAUDT等[24]对Halite相进行了研究，结果表明Al2O3和SiO2在Halite相中具有一定溶解度。然而，考虑到该实验数据较少，PELTON[25]对MgO-SiO2体系的评估中，忽略了SiO2在Halite相中的溶解度。SCHREYER等[22]发现Sap在1 465 ℃时熔融形成液相和Mul相，并根据实验结果给出了Cord-Mul、Ppx-Cord、Oli-Cord、Cord-SiO2和Spi-Cord等一系列垂直截面数据。

SCHREYER等[22]对两个零变量反应Cord+Tri→ Mul+Liq和Cord+Ppx+Tri→Liq的温度进行了实验研究。FOSTER[20]也对Sap相的熔化反应进行了研究，发现该相在1 475 ℃时熔融形成Spi相和液相。SMART等[26]报道了Cord相固溶体在较小成分、温度范围内的相平衡。本研究未考虑Cord相和Sap相的固溶度，均处理为线性化合物。此外，SAXENA等[27]和GOTTSCHALK[28]分别报道了Cord相和Sap相的标准熵与热容数据，其结果被本工作采用。

OSBORN等[29]提出了Al2O3-SiO2-MgO体系液相面投影图。FOSTER[20]和SMART等[30]利用烧结技术和XRD分别研究了Al2O3-SiO2-MgO体系固相平衡。FOSTER等[20]研究了反应Sap+Corundum=Spi+Mul。反应Cord+Corundum=Mul+Sp由SMART等[30]研究。SMART等[30]研究了零变量反应的温度和Cord相的熔点。FOSTER等[20]实验测定了1 460 ℃的等温截面。SMART等[30]提供了1 350、1 450、1 470、1 490、1 525和1 575 ℃的一系列等温截面。SMART[26]研究了垂直截面MgSi2O5-Mg2Al4Si5O18和Mg7Al22O40-SiO2。GREIG[19]对液相混溶间隙进行了实验研究。研究表明，MgO-SiO2体系中少量氧化铝的加入会显著减小混溶间隙，并且两种液相共存时(Al2O3)不超过5% ((Al2O3)≈2.89%)。

HENDERSON等[31]通过1 500 ℃和1 550 ℃下SiO2+3C=SiC+2CO平衡时的CO压强研究了Al2O3- SiO2-MgO体系液相中SiO2的活度。REIN等[32]通过 1 600 ℃下Si在Fe-Si-C合金中的分布研究了Al2O3- SiO2-MgO体系液相中SiO2的活度。然而，两者研究结果之间存在明显差异。一般来说，由于动力学相对缓慢，很难再现测量高黏度玻璃熔体热力学性质的结果。因此，在本工作热力学优化过程中，并未采用活度的实验数据。本工作采用SMART等[30]、OSBORN等[29]、SCHREYER等[22]的数据。

2 热力学模型

本工作采用下述热力学模型对Al2O3-MgO和Al2O3-MgO-SiO2体系进行重新评估。

2.1 纯组元热力学模型

纯组元的吉布斯自由能G()可表示为：

表1 Al2O3-MgO-SiO2体系中各相

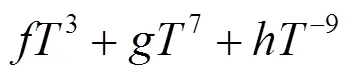
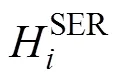
2.2 液相

本研究采用离子双亚点阵模型描述液相，Al2O3-MgO二元系的液相模型为(Al+3,Mg+2)P(AlO2−1,O−2)Q。HILLERT等[33]和SUNDMAN[34]将Al2O3-SiO2-MgO体系的液相描述为(Al+3,Mg+2)P(AlO2−1,O−2,SiO4−4,SiO20)Q，本工作采用该模型。

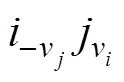
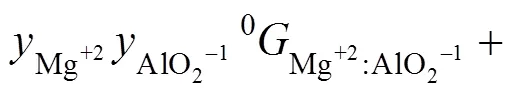
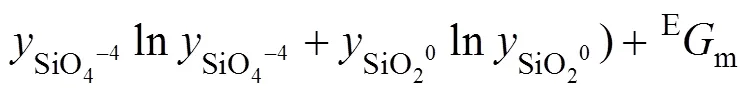
式中：表示点阵分数；0表示端际组元的吉布斯自由能，kJ/mol；Em为超额吉布斯能，kJ/mol。

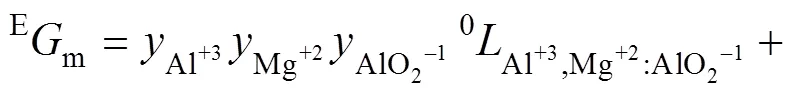
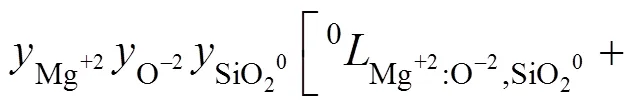
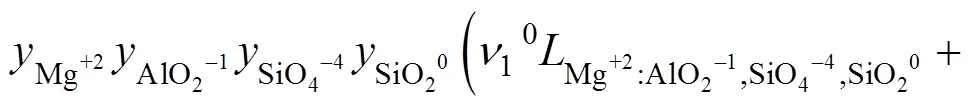
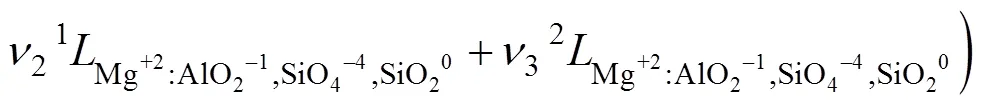
式中：(=0, 1, 2, 3)表示每个亚点阵内组元之间的相互作用；(=1, 2, 3)是成分变量，定义为：其中的。

除了离子双亚点阵液相模型外，研究者还提出许多其他液相热力学模型，包括修正的准化学模型[35]、Gaye-Kapoor-Frohberg模型[36]、缔合溶液模型[37−39]、液相络合物的多项式表示[40]，以及化学计量−马格里斯溶液模型(Margules溶液模型)[41]。大多数模型都能很好地再现二元相图，但他们从二元体系扩展到多组元时对于液相混溶间隙的描述与实验结果存在出入，本文中不再详细介绍。

2.3 化学计量化合物

Cord和Sap视作化学计量化合物，吉布斯自由能由下式给出：

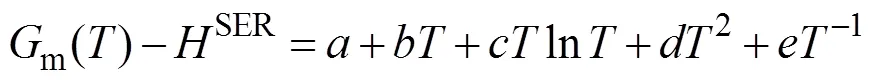
2.4 固溶体

固溶体相Halite用化合物能量模型(compound energy formalism, CEF)来描述，CEF中每摩尔分子的吉布斯能量表达式为：

式中：1和2是每单位溶液的第一个和第二个亚点阵的点阵个数。E扩展为：

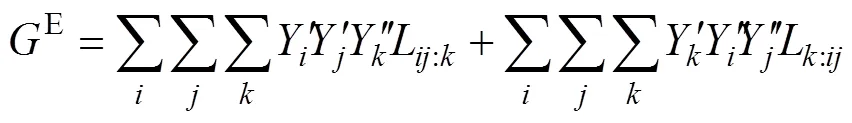
本研究中，将Cord和Sap视作线性化合物，Spinel、Mullite和Halite在各自的二元体系中被视为固溶体，但没有第三组分的溶解度，Spinel相采用ZIENERT等[10]的参数，Mullite相采用MAO等[42]的参数。

3 优化结果与讨论

本工作利用Thermo-calc软件中的PARROT模 块[5]，对Al2O3-MgO二元系和Al2O3-MgO-SiO2三元系进行优化。

3.1 Al2O3-MgO体系优化

在ZIENERT等[10]的研究基础上对Halite相参数进行优化改进。液相采用MAO等[9]的热力学模型来描述：(Al+3,Mg+2)P(AlO2-1,O-2,)Q，并对液相参数进行优化调整。

热力学优化过程中，本工作考虑了ALPER等[13]、VIERTEL等[18]、毛利尚彦[43]和FUJII等[44]的数据，以适当的权重输入各项实验信息，首先通过液相线的实验数据调整液相参数，再结合Halite相的固相线数据对其参数进行调整，最后得到一套自洽的热力学参数。优化后Al2O3-MgO二元系中Halite相和液相的热力学参数见表3。

本工作优化得到的Al2O3-MgO体系相图及与文献中实验数据的比较如图1所示。计算得到包晶反应Liquid + Corundum = Spinel温度为1 998 ℃，计算得到共晶反应Liquid = Halite + Spinel温度为1 997 ℃。表2所列为零变量反应的温度和相组成以及实验数据。可见，本工作计算得到的结果可以合理地描述大部分实验相图信息。

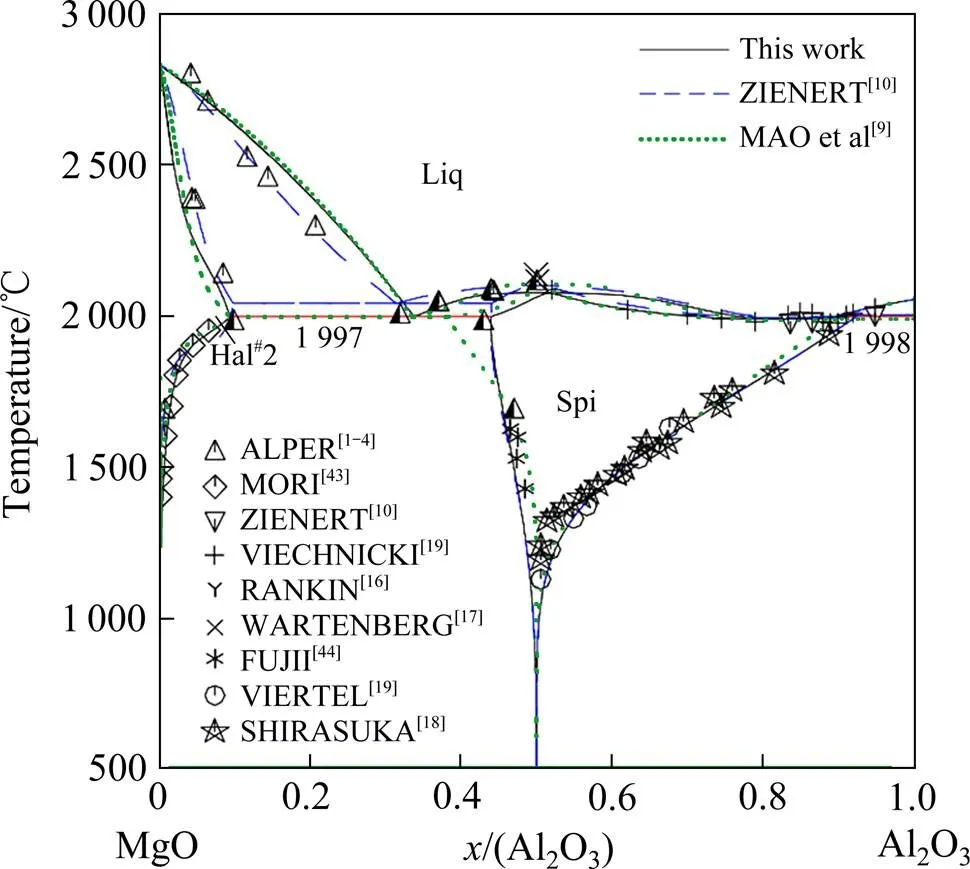
图1 优化后的Al2O3-MgO体系相图与MAO等[9]、ZIENERT等[10]的计算结果和实验数据比较

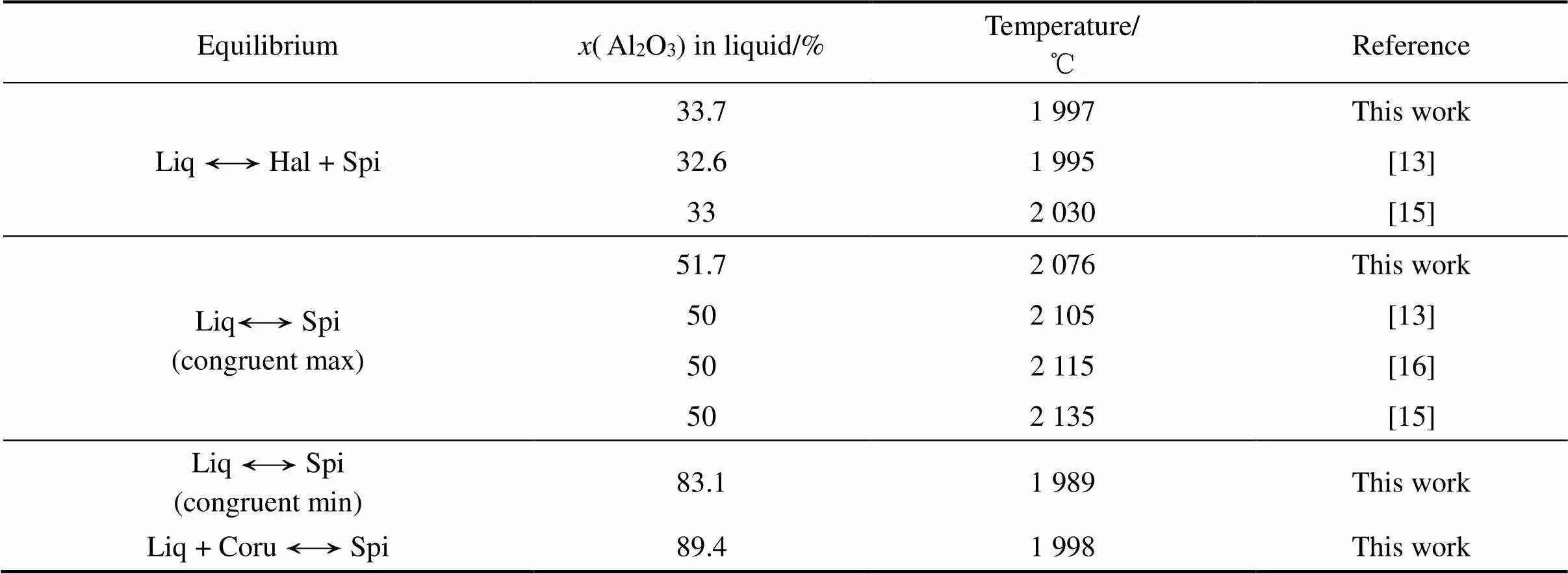
表2 Al2O3-MgO体系中零变量平衡

3.2 Al2O3-MgO-SiO2三元体系优化

本工作采用的Al2O3-SiO2和MgO-SiO2体系的热力学参数分别取自MAO等[11]和HUANG等[45]的数据。图2和图3分别为计算得到的Al2O3-SiO2和MgO- SiO2体系相图。Al2O3-MgO二元系采用本工作优化后的结果。Al2O3-MgO-SiO2体系的液相描述为(Al+3, Mg+2)P(AlO2−1,O−2,SiO4-4,SiO20)Q。

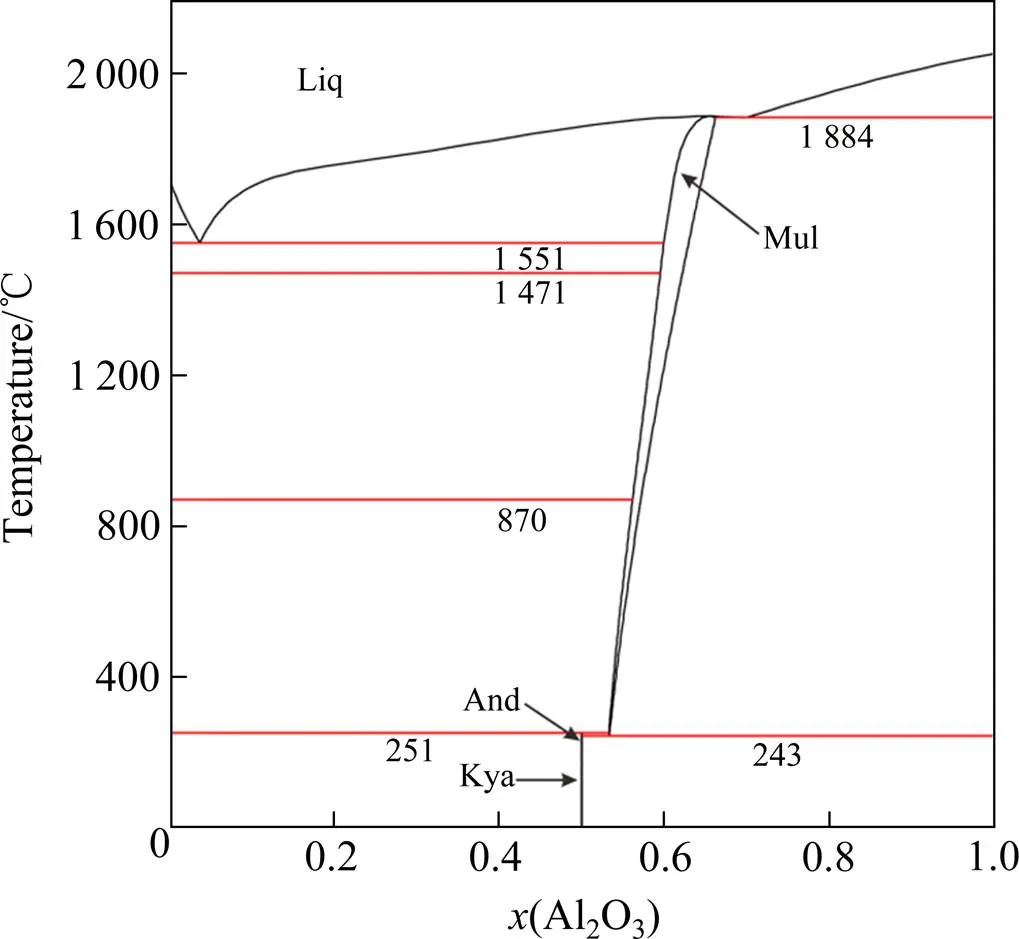
图2 计算的Al2O3-SiO2体系相图[46]

根据零变量反应对两个三元化合物的参数进行优化调整。热力学优化过程综合考虑SMART等[30]和OSBORN等[29]的数据。通过输入各项实验数据并对其赋以合适的权重，首先调整液相参数，再调整三元化合物参数，得到一套自洽的热力学描述，如表3所列。基于所得的热力学参数，计算Al2O3-MgO-SiO2体系的相图和热力学性质。图4为计算的Al2O3-MgO-SiO2体系液相线投影图，图中零变量反应的信息及其与实验数据的对比列于表4。可以看出，对于共晶点和包晶点，计算结果与实验信息[29]吻合较好。本工作计算结果是1 700 ℃时，液相混溶间隙(Al2O3)为7%，而GREIG[19]实验数据是1 600 ℃时，混溶间隙(Al2O3)为5%，本工作比JUNG等[8]和FABRICHNAYA等[46]计算的混溶间隙与实验数据更接近。图5为计算所得不同温度的等温截面，计算结果与实验数据[30]在误差允许范围内吻合较好。图6～10为计算的一系列垂直截面与实验数据的对比，可以看出计算结果与实验数据相差不大。因此，本工作优化得到的热力学参数是合理可靠的。

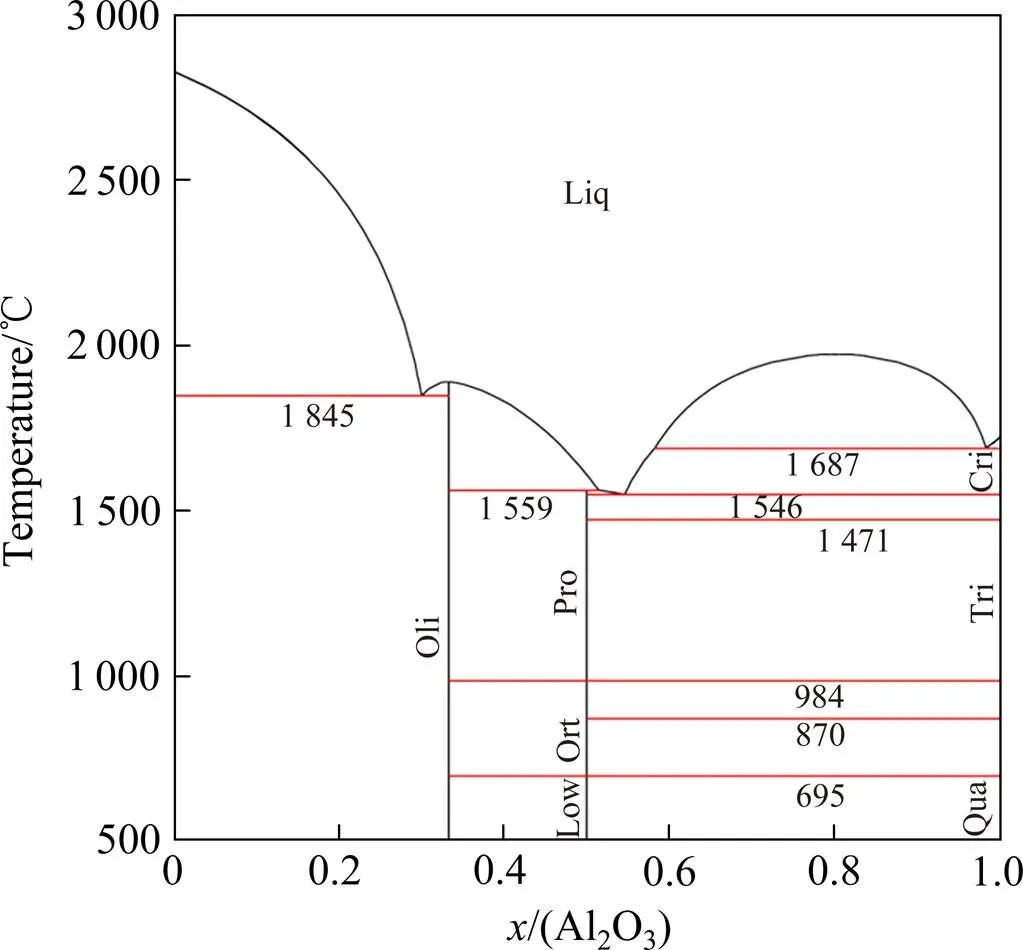
图3 计算的MgO-SiO2体系相图[45]

表3 优化所得Al2O3-MgO二元系和Al2O3-MgO-SiO2体系中各相的热力学参数

续表3

图4 计算所得Al2O3-MgO-SiO2体系液相面投影图

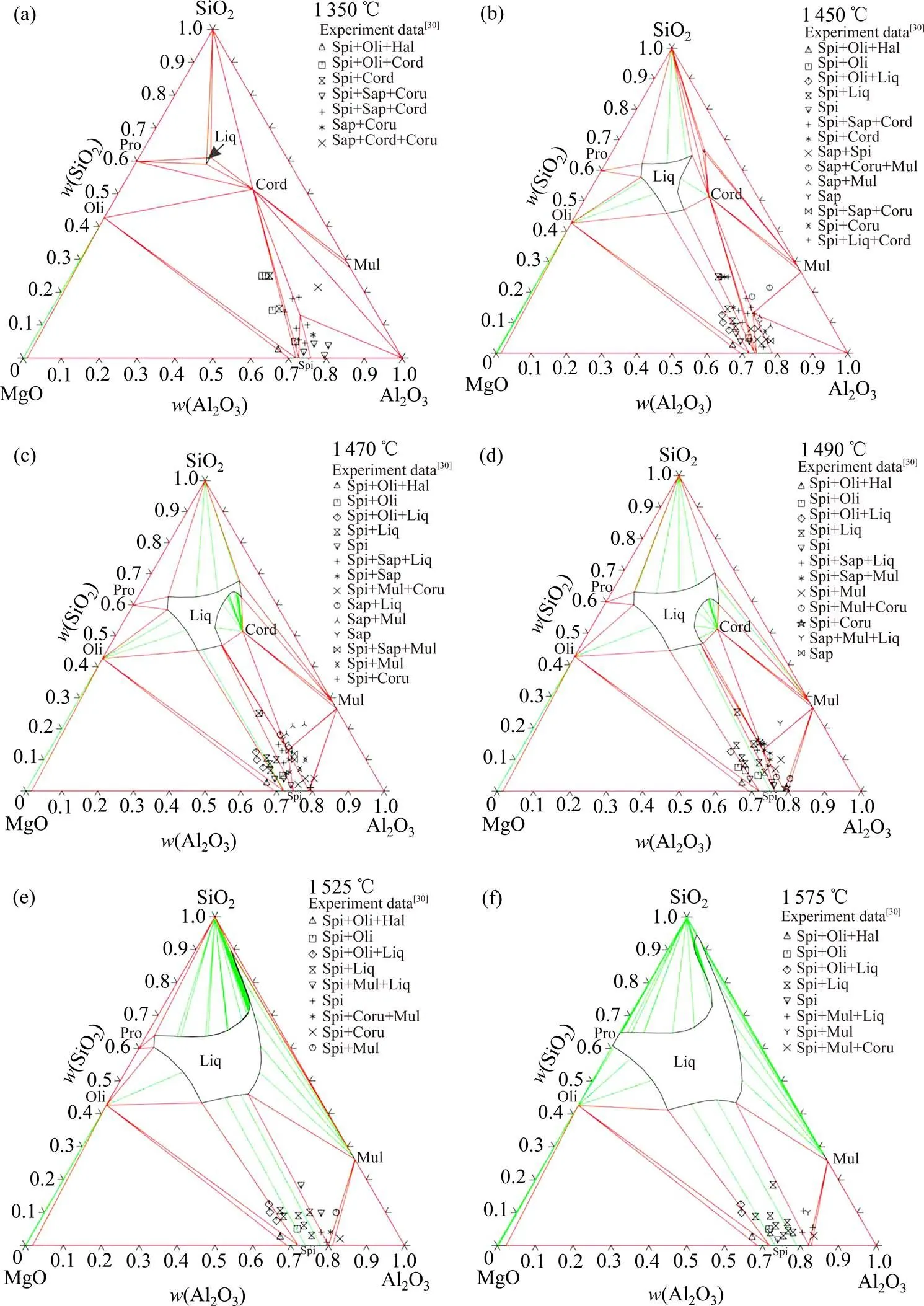
图5 计算所得Al2O3-MgO-SiO2体系相图及与实验数据[30]的对比

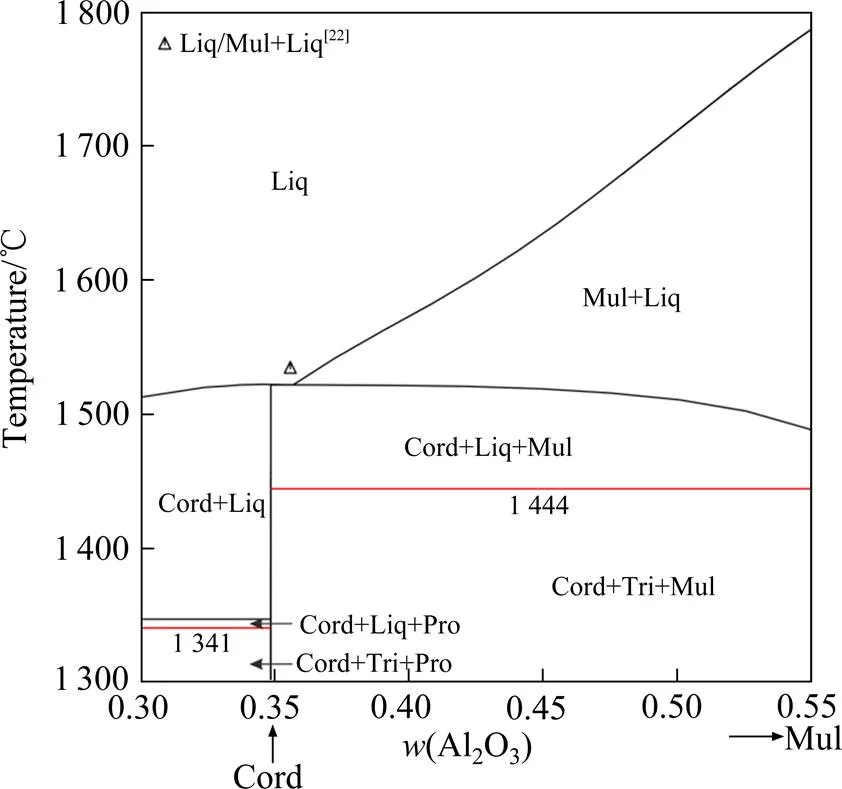
图6 计算所得Cord-Mul截面相图及与实验数据[22]的对比

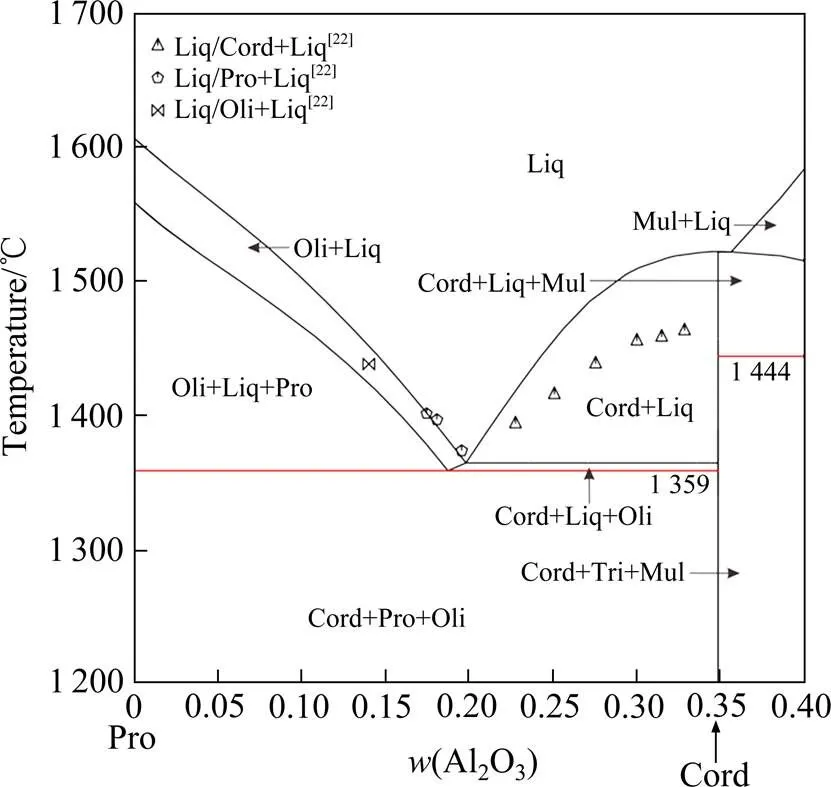
图7 计算所得Pro-Cord截面相图及与实验数据[22]的对比

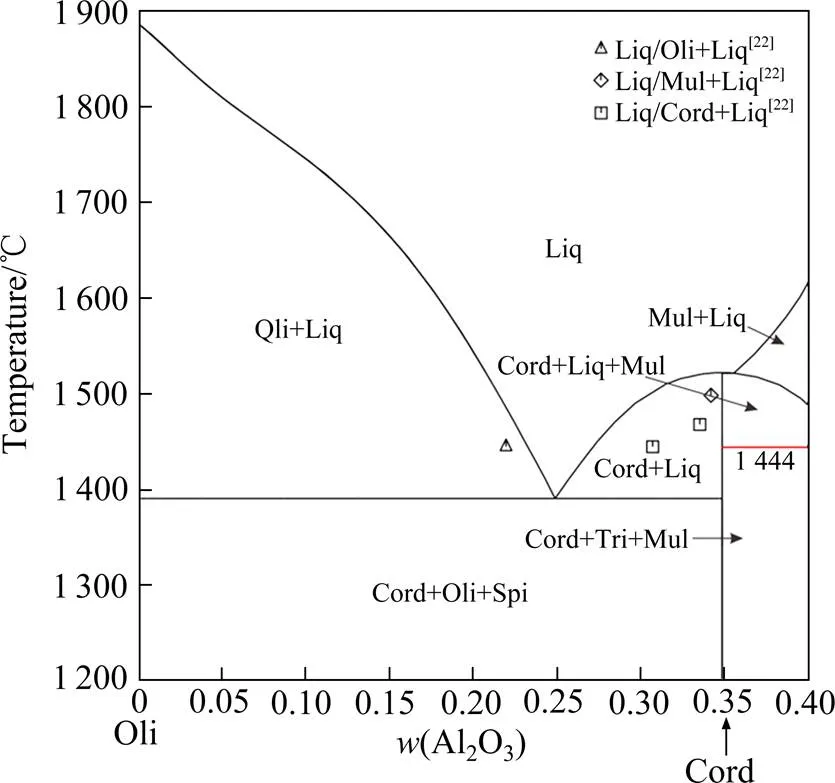
图8 计算所得Oli-Cord截面相图及与实验数据[22]的对比

图9 计算所得Cord-SiO2截面相图及与实验数据[22]的对比

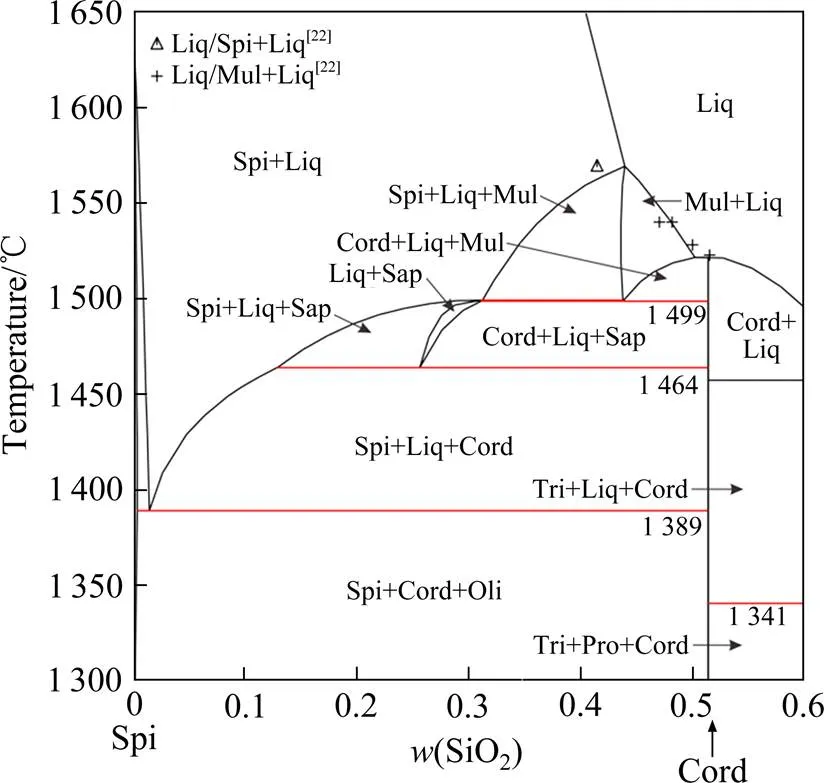
图10 计算所得Spi-Cord截面相图及与实验数据[22]的对比

4 结论

1) 本工作基于对Al2O3-MgO和Al2O3-SiO2-MgO体系的相平衡实验数据进行评估，通过CALPHAD方法对其进行热力学优化，得到了一套自洽的热力学参数。

2) 相较于文献报道的计算结果，本工作所得的热力学参数和Al2O3-MgO体系相图与实验结果吻合更好，并在外推至多元系时能更好地描述液相混溶间隙。计算所得Al2O3-SiO2-MgO体系相图能够更准确合理地吻合实验信息。

3) 本工作所得Al2O3-SiO2-MgO体系的热力学描述可以为固废材料重构转化提供关键理论知识，为Al2O3-SiO2-MgO-CaO-Fe2O3-Na2O六元体系热力学数据库的构建提供基础指导，对固废材料的高值化应用具有一定的理论指导作用。

表4 Al2O3-MgO-SiO2体系中零变量平衡

[1] 刘本甫, 盖建功. 我国工业固废现状及综合利用建议[J]. 中国资源综合利用, 2018, 36(6): 92−93.

LIU Benfu, GAI Jiangong. China’s industrial solid waste status and comprehensive utilization recommendations[J]. China Resources Comprehensive Utilization, 2018, 36(6): 92−93.

[2] 晏全香. 尾矿再利用中铝硅酸盐矿物处理现状研究[J]. 中国矿业, 2011, 20(7): 59−61.

YAN Quanxiang. Research on reclaiming tailings in the treatment of aluminumsilicat[J]. China Mining Magazine, 2011, 20(7): 59−61.

[3] 贾敏. 煤矸石综合利用研究进展[J]. 矿产保护与利用, 2019, 39(4): 46−52.

JIA Min. The current situation research on comprehensive utilization of coal gangue[J]. Conservation and Utilization of Mineral Resources, 2019, 39(4): 46−52.

[4] KAUFMAN L, BEMSTEIN H. Computer Calculation of Phase Diagram[M]. New York: Academic Press, 1970.

[5] ANDERSSON JO, HELANDER T, HöGLUND L, et al. Thermo-Calc and DICTRA, computational tools for materials science[J]. Calphad, 2002, 26(2): 273−312.

[6] 刘树红, 金波, 傅太白, 等. 相图热力学数据库及其计算软件:过去、现在和将来[J]. 中国科学:化学, 2019, 49(7): 966−977.

LIU Shuhong, JIN Bo, FU Taibai, et al. Thermodynamic databases and software: past, present and future[J]. Science in China: Chemistry, 2019, 49(7): 966−977.

[7] HALLSTEDL B. Assessment of the CaO-Al2O3system[J]. Journal of the American Ceramic Society, 1990, 73(1): 15−23.

[8] JUNG IH, DECTEROV S A, PELTON A D. Critical thermodynamic evaluation and optimization of the MgO-Al2O3, CaO-MgO-Al2O3, and MgO-Al2O3-SiO2systems[J]. Journal of Phase Equilibria and Diffusion, 2004, 25(4): 329−345.

[9] MAO H, SELLEBY M, SUNDMAN B. A re-evaluation of the liquid phases in the CaO-Al2O3and MgO-Al2O3systems[J]. Calphad, 2004, 28(3): 307−312.

[10] ZIENERT T, FABRICHNAYA O. Thermodynamic assessment and experiments in the system MgO-Al2O3[J]. Calphad, 2013, 40: 1−9.

[11] MAO H H, FABRICHNAYA A, SELLEBY M, et al. Thermodynamic assessment of the MgO-Al2O3-SiO2system[J]. Journal of Materials Research, 2005, 20 (4): 975−986.

[12] RANKIN G, MERWIN H. The ternary system CaO-Al2O3-MgO [J]. Journal of the American Chemical Society, 1916, 38(3): 568−588.

[13] ALPER A, MCNALLY R, RIBBE P, et al. The system MgO-MgAl2O4[J]. Journal of the American Ceramic Society, 1962, 45(6): 263−268.

[14] VIECHNICKI D, SCHMID F, MCCAULEY J. Liquidus-solidus determinations in the system MgAl2O4-Al2O3[J]. Journal of the American Ceramic Society, 1974, 57(1): 47−48.

[15] RANKIN G A, MERWIN H E. The ternary system MgO-Al2O3-SiO2[J]. American Journal of Science, 1918, 45(268): 301−325.

[16] WARTENBERG H V, GURR W. Schmelzdiagramme höchstfeuerfesteroxyde. III[J]. Zeitschrift für Anorganische und Allgemeine Chemie, 1931, 196(1): 374−383.

[17] SHIRASUKA K, YAMAGUCHI G. Precise measurement of the crystal data and the solid solution range of the defective spinel, MgO· nAl2O3[J]. Journal of the Ceramic Society of Japan, 1974, 82: 650−653.

[18] VIERTEL H, HU V. Thermal stability of defect spinels in the system MgAl2O4-Al2O3[J]. Neues Jahrbuch fur Mineralogie, Abhandlungen, 1980, 140: 89−101.

[19] GREIG J W. Immiscibility in silicate melts:part I[J]. American Journal of Science, 1927, 5(73): 1−44.

[20] FOSTER W. Synthetic sapphirine and its stability field in the system MgO-Al2O3-SiO2[J]. Journal of Smerican Ceramic Society, 1950, 33(3): 73−84.

[21] KEITH M, SCHAIRER J. The stability field of sapphirine in the system MgO-Al2O3-SiO2[J]. The Journal of Geology, 1952, 60(2): 181−186.

[22] SCHREYER W, SCHAIRER J F. Compositions and structural states of anhydrous Mg-Cordierites: a re-investigation of the central part of the system MgO-Al2O3-SiO2[J]. Journal of Petrology, 1961, 2(3): 324−406.

[23] ARAMAKI S, ROY R. The Mullite-Corundum boundary in the systems MgO-Al2O3-SiO2and CaO-Al2O3-SiO2[J]. Journal of the American Ceramic Society, 1959, 42(12): 644−645.

[24] SCHLAUDT C M, ROY D M. Crystalline solution in the system MgO-MgSiO4-MgAl2O4[J]. Journal of the American Ceramic Society, 1965, 48(5): 248−251.

[25] PELTON A D. A general “geometric” thermodynamic model for multicomponent solutions[J]. Calphad, 2001, 25 (2): 319−328.

[26] SMART R, GLASSER F. The subsolidus phase equilibria and melting temperatures of MgO-Al2O3-SiO2compositions[J]. Ceramics International, 1981, 7(3): 90−97.

[27] SAXENA S, CHATTERJEE N, FEI Y, et al. Thermodynamic data on oxides and silicates[J]. Crystal Research and Technology, 1995, 30(7): 83−84.

[28] GOTTSCHALK M. Internally consistent thermodynamic data for rock-forming minerals in the system SiO2-TiO2-Al2O3-Fe2O3- CaO-MgO-FeO-K2O-Na2O-H2O-CO2[J]. European Journal of Mineralogy, 1996, 175−223.

[29] OSBORN E, MUAN A. Specific diagrams B. metal oxide systems[J]. Phase Diagrams for Ceramists, 1964, 1: 264−264.

[30] SMART R, GLASSER F. Phase relations of cordierite and sapphirine in the system MgO-Al2O3-SiO2[J]. Journal of Materials Science, 1976, 11(8): 1459−1464.

[31] HENDERSON D, TAYLOR J. Thermodynamic properties in the CaO-MgO-SiO2and MgO-Al2O3-SiO2systems[J]. Journal of Iron and Steel Institute, 1966, 204(1): 39−43.

[32] REIN R H, CHIPMAN J. Activities in the liquid solution SiO2-CaO-MgO-Al2O3at 1 600 ℃[J]. Transactions of the Metallurgical Society of AIME, 1965, 233(2): 415−425.

[33] HILLERT M, JANSSON B, SUNDMAN B, et al. A two-sublattice model for molten solutions with different tendency for ionization[J]. Metallurgical Transactions A, 1985, 16(2): 261−266.

[34] SUNDMAN B. Modification of the two-sublattice model for liquids[J]. Calphad, 1991, 15(2): 109−119.

[35] PELTON A D, BLANDER M. Thermodynamic analysis of ordered liquid solutions by a modified quasichemical approach-application to silicate slags[J]. Metallurgical Transactions B, 1986, 17(4): 805−815.

[36] GAYE H. Modeling of the thermodynamic properties of complex metallurgical slags[J]. Journal of Metals, Materials and Minerals, 1984, 36(8): 88−88.

[37] LARRAIN J, KELLOGG H. Use of chemical species for correlation of solution properties[J]. Calculation of Phase Diagrams and Thermochemistry of Alloy Phases, 1979: 130−144.

[38] BJöRKMAN B. An assessment of the system FeO-SiO2using a structure based model for the liquid silicate[J]. Calphad, 1985, 9(3): 271−282.

[39] HASTIE J, HORTON W, PLANTE E, et al. Thermodynamic models of alkali-metal vapor transport in silicate systems[J]. High Temperatures High Pressures (Print), 1982, 14(6): 669− 679.

[40] HOCH M. Application of the Hoch-Arpshofen model to the SiO2-CaO-MgO-Al2O3system[J]. Calphad, 1988, 12 (1): 45−58.

[41] BERMAN R G. A thermodynamic model for multicomponent melts, with application to the system CaO-Al2O3-SiO2[J]. Geochimica et Cosmochimica Acta, 1984, 48 (4): 661−678.

[42] MAO H, SELLEBY M, SUNDMAN B. Phase equilibria and thermodynamics in the Al2O3-SiO2system-modeling of mullite and liquid[J]. Journal of the American Ceramic Society, 2005, 88(9): 2544−2551.

[43] 毛利尚彦. MgO-Al2O3の固溶[J]. 窯業協會誌, 1982, 90(1045): 551−552.

MORI T. Solubility of Al2O3in MgO[J]. Journal of Kiln Industry Association, 1982, 90(1045): 551−552.

[44] FUJII K, NAGASAKA T, HINO M. Activities of the constituents in spinel solid solution and free energies of formation of MgO, MgO-Al2O3[J]. ISIJ International, 2000, 40(11): 1059−1066.

[45] HUANG W, HILLERT M, WANG X. Thermodynamic assessment of the CaO-MgO-SiO2system[J]. Metallurgical and Materials Transactions A, 1995, 26(9): 2293−2310.

[46] FABRICHNAYA O, E SILVA A C, ALDINGER F. Assessment of thermodynamic functions in the MgO-Al2O3-SiO2system[J]. Zeitschrift fur Metallkunde, 2004, 95(9): 793−805.

Thermodynamic optimization and calculation of the Al2O3-MgO and Al2O3-MgO-SiO2systems

MA Tianyi, LIU Yuling, GAO Fengyang, ZHANG Liang, DU Yong

(State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China)

Since the thermodynamic parameters of Al2O3-MgO binary system in the reported literatures deviated from the experimental data when it was extrapolated to the multivariate system, the calculation of phase diagram (CALPHAD) method was used in this work to re-optimize the system based on the rigorous evaluation of the thermodynamic data. Subsequently, the thermodynamic description of the Al2O3-MgO-SiO2system was further improved. In the optimization process, the ionic two-sublattice model was used to describe the liquid phase and compound energy formalism (CEF) model was used to describe the solid phase. The results of thermodynamic optimization and calculation of Al2O3-MgO and Al2O3-MgO-SiO2phase diagrams are in good agreement with most experimental data. This work is the basis of constructing a thermodynamic database of Al2O3-SiO2-MgO-CaO-Fe2O3-Na2O system, and can provide guidance for the high-value utilization of bulk aluminosilicate solid waste.

Al2O3-MgO-SiO2system; Al2O3-MgO system; thermodynamic optimization; CALPHAD; phase diagram calculation

10.19976/j.cnki.43-1448/TF.2022034

TB321

A

1673-0224(2022)04-360-12

国家重点研发项目(2019YFC1904901)

2022−03−30；

2022−05−06

刘钰玲，讲师，博士。电话：18711084610；E-mail: liu.yuling@csu.edu.cn

(编辑 陈洁)