短碳纤维增强铜复合材料的计算细观力学模型及力学性能
2022-12-08何东浪方华婵李郁兴李金伟
何东浪,方华婵,李郁兴,李金伟
短碳纤维增强铜复合材料的计算细观力学模型及力学性能
何东浪,方华婵,李郁兴,李金伟
(中南大学 粉末冶金国家重点实验室,长沙 410083)
针对粉末冶金法制备的短碳纤维增强铜复合材料(CSf/Cu),采用有限元方法建立细观力学模型,研究材料的拉伸损伤演化和断裂力学行为,并分析弱界面对复合材料拉伸性能的影响。结果表明,CSf/Cu复合材料的拉伸过程可分为弹性阶段、塑性硬化阶段、起始损伤阶段和损伤演化阶段。纤维端部的应力集中造成端部界面脱黏、轴向界面的损伤演化以及纤维桥联,基体损伤及其伴随的界面损伤造成基体破坏是材料断裂的主要机制。碳纤维长度大于60 μm时,纤维的轴向应力分布呈现“w”形,纤维有较强的承载能力;纤维长度为20 μm时,纤维几乎没有承载能力。纤维承受载荷越高,越容易造成界面破坏,随纤维长度从20 μm增加到140 μm,Csf/Cu复合材料的抗拉强度从146 MPa下降到102 MPa。
短纤维;铜基复合材料;细观力学;有限元;内聚力单元
短碳纤维/铜复合材料兼具铜的高导热、导电性能以及碳纤维的高比模量和高比强度,因此具有优异的力学性能、耐磨性能和良好的导热性能,广泛应用于高效散热器、电接触材料和耐磨器等[1]。然而,目前还没有一种精确的方法来预测碳纤维/铜复合材料的强度,特别是随机短纤维复合材料。一般来说,采用实验方法获取的力学性能是不全面的,仅能获得个别材料的模量、强度等性能参数,不能可视化局部应力场,无法揭示复合材料的起始损伤和演化过程。因此,迫切需要一种准确且经济有效的方法来揭示复合材料的损伤起始和演化过程,进而预测其强度。近年来,随着计算机技术和有限元方法的迅速发展,计算细观力学逐渐成为了解复合材料损伤过程和预测材料强度的有效工具。与经典均匀化技术相比,计算细观力学具有2个重要优势。首先,可以准确地考虑增强相的几何形状和空间分布的影响;其次,可揭示整个细观结构中应力场和应变场的细节,从而精确估计损伤的开始和传播,并准确预测失效强度。
前人已经对短纤维增强复合材料的力学性能进行了大量研究,包括提出新的建模方法[2],采用扩展有限元研究界面渐进损伤过程[3−6]、细观力学分析局部应力场[7−13]和预测刚度、强度[14−15]等。在短纤维增强复合材料细观力学方面,GAO等[8]运用随机顺序吸附算法建立短芳纶纤维增强橡胶复合材料的有限元模型,研究大长径比的短芳纶纤维和橡胶大变形状态下的局部应力场和宏观力学响应,但未考虑材料界面的影响。TIAN等[9]研究了界面厚度、界面模量和短纤维取向对纤维最大轴向应力的影响,发现短纤维的最大轴向应力位于纤维中心,从中心向两端逐渐减小。REDDY等[16]采用代表性体积单元(representative volume element, RVE)方法建立三维有限元模型,研究了纤维体积分数对材料弹性模量和切变模量的影响。YANG等[10]采用细观力学模型和弹塑性有限元分析方法,研究短纤维增强复合材料的局部弹塑性应力场,以了解纤维之间和纤维与基体之间的非弹性变形和相互作用机理。LEI等[17]生成了纤维随机分布的复合材料微观结构的代表性体积单元,揭示复合材料的损伤过程以及不同损伤机制之间的相互作用。碳和铜既不发生化学反应,也不互溶,且碳和铜即便在液态下润湿性也极差,因此碳纤维增强铜复合材料中碳纤维和铜基体的界面是极弱界面,但上述研究都只考虑了基体和纤维的影响,将界面假设为完美界面,未考虑弱界面及其损伤演化对力学性能的影响,也没有采用多尺度分析来阐述材料的失效过程。本文作者建立短纤维增强铜复合材料(Csf/Cu)在拉伸作用下的细观力学弹塑性−损伤模型。从应力−应变曲线获得复合材料的强度,通过不同载荷水平下的损伤状态清楚地揭示出复合材料的起始损伤和演化过程。然后进行参数化研究,以评估纤维长度及Csf/Cu弱界面对应力−应变曲线、局部应力场和损伤萌生及演化行为的影响。相比于以往的研究,本文充分考虑Csf/Cu弱界面对复合材料力学性能的影响,并完整地研究拉伸过程中弹性阶段、塑性硬化阶段、起始损伤阶段和损伤演化阶段的力学行为,清晰地展现加载过程中应力场的变化情况,为材料的进一步设计和优化提供理论依据。
1 材料本构方程
1.1 界面损伤的演化本构
采用内聚力(cohesive)单元描述碳纤维增强铜复合材料中铜基体与碳纤维之间的界面损伤与脱黏行为。商用有限元分析软件ABAQUS中的内聚区采用一层厚度接近零的内聚力单元表示,内聚力单元可以灵活地嵌入到传统单元之间,单元的上下表面与相邻单元连接,外力引起的材料损伤限制在内聚力单元内,其他单元不受影响。用内聚单元表示Csf/Cu基复合材料的Csf/Cu界面脱黏。界面上节点的牵引应力和分离位移受牵引分离规律控制。界面的牵引应力包括一个正常牵引力和两个剪切牵引力。名义应力由n、s和t三个分量组成,分别代表法向和两个剪切方向上的名义应力。相对应的位移分离量记为n、s和t。内聚力单元的原始厚度记为0,名义应变的3个分量分别定义为:
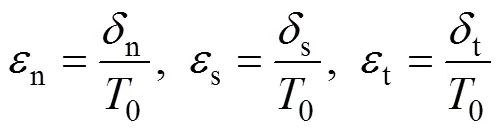
Csf/Cu界面损伤的演化本构关系可用图1所示曲线描述,图中描述了内聚力单元的双线性模型。从图中本构可将界面损伤演化分为3个阶段,即弹性阶段、初始损伤及损伤演化。其中弹性阶段的本构方程表示如下:

ns和t分别代表法向和两个剪切方向上的名义应力。当弹性阶段结束时起始损伤开始,即意味着材料退化的开始。当应力或应变满足某个起始损伤准则时,起始损伤发生。本文采用最大应力准则,作为材料损伤的起始判据:
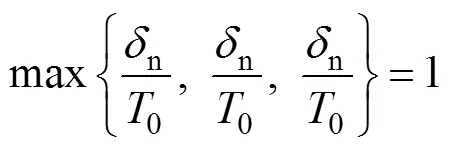
当内聚力单元的应力状态满足起始损伤准则后,单元即发生损伤,然后进入损伤演化阶段。针对内聚力单元的损伤演化,为了表示材料的整体损伤,给出损伤变量。的初始值为0,表示没有发生损伤。如果在起始损伤后,损伤演化继续发生,随着载荷加载,损伤变量从0到1单调增加。当达到1时表明单元完全失效,失去承载能力。
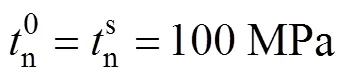
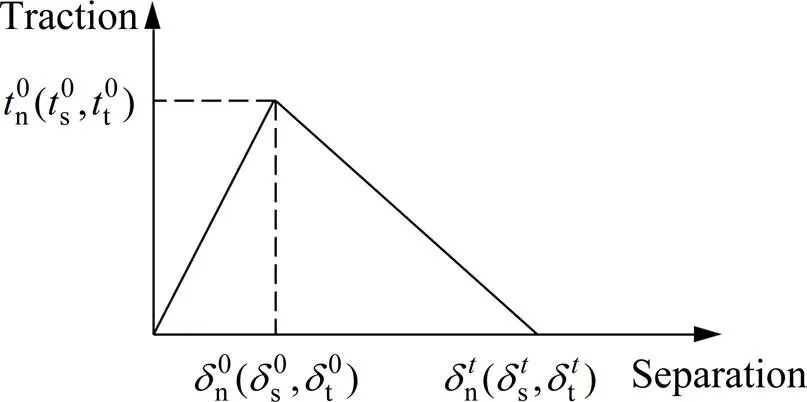
图1 Csf/C界面损伤的cohesive双线性本构曲线
1.2 铜基体的渐进损伤本构
铜是典型的各向同性延性金属,因此采用改进后的Drucker-Prager模型[18]来描述铜的弹塑性及损伤破坏行为,得到图2所示的Csf/Cu复合材料受到损伤时的应力−应变特性。图中实曲线为损伤应力−应变响应,虚线为无损伤情况下的响应。


图2 铜基体的渐进性退化损伤应力−应变曲线


表1 铜和碳纤维的主要参数
2 多尺度有限元模型
2.1 代表性体积单元的选取
本文研究的短碳纤维增强铜复合材料,纤维随机分布在基体中,因此采用随机序列吸附方法(random sequential adsorption, RSA )生成随机纤维。随机序列吸附方法的主要思想是在基体单胞中逐个加入增强体,每次加入新的随机生成的增强体,判断其是否和已存在的增强体相交。如果有相交,则重新生成当前增强体的位置和取向,再判断是否和已存在的增强体相交。如此循环,直到新生成的增强体与之前存在的增强体都不相交,则接受当前的增强体,记录下该增强体的位置和取向,作为已存在的增强体之一。
为了保持RVE的代表性,同时又不至于让几何结构过于复杂,采用RSA方法在ABAQUS中生成了25根纤维,纤维直径都为7 μm,纤维长度可调整,纤维占比(体积分数)固定为9%。基体的长和宽相同,由纤维占比来调控基体尺寸。随后采用ABAQUS二次开发的子程序对Csf/Cu界面批量插入cohesive单元,从而得到Csf/Cu复合材料的代表性体积单元(representative volume, RVE),如图3所示。
2.2 复合材料有效性能的计算方法
代表性体积单元(RVE)的平均应力计算公式为:
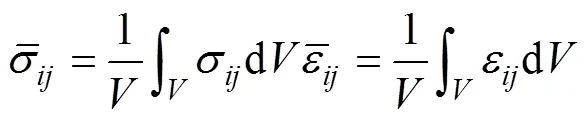
RVE的平均应变计算公式为:
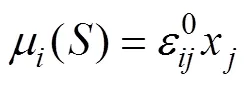
式中:μi(S)为RVE的位移;为RVE的应变;xj为RVE的长度。
在 ABAQUS 的有限元模型计算结果中,提取出参考点在拉伸方向上的位移和支撑反力−位移曲线,进一步处理后得到复合材料单胞模型的应力−应变曲线,用于表征复合材料的有效力学性能。
3 结果与讨论
3.1 拉伸应力−应变曲线及细观损伤过程
应力−应变曲线反映了Csf/Cu复合材料在拉伸载荷作用下的宏观力学行为。在拉伸实验中,粉末冶金法制备的Csf/Cu复合材料往往表现出脆性断裂特征,拉伸应力−应变曲线在达到最大应力后迅速下降。为了揭示材料从开始加载到失效的演化过程以及碳纤维长度、弱界面等因素对演化过程的影响,本文采用多尺度分析的方法,即把宏观力学分析和细观力学分析结合起来,获得Csf/Cu复合材料在不同拉伸载荷下的平均应力−应变、局部应力场和损伤机理的详细信息。为了清晰地呈现材料失效演化过程,选取纤维长度为60 μm的Csf/Cu复合材料进行多尺度力学分析。结果表明,由于材料的不连续性,在纤维端部附近存在很高的Van Mises应力区,容易引起纤维与基体界面脱黏。随塑性变形增加,高应力区域扩大。Csf/Cu复合材料的拉伸应力−应变曲线根据其细观力学行为可分为4个阶段:弹性阶段、塑性硬化阶段、起始损伤阶段和损伤演化阶段。
图4所示为纤维长度为60 μm 的CSf/Cu复合材料拉伸应力−应变曲线细观状态的4个阶段。从图4(a)可知,在弹性阶段,基体应力小于基体的屈服强度,碳纤维和铜基体产生协调变形,Csf/Cu界面承受的应力较小而未被破坏,纤维承受大部分应力。从图4(b)可知,随载荷进一步增大,纤维端部附近的铜基体应力达到屈服极限,进入塑性硬化阶段,而碳纤维仍处于弹性阶段,铜基体的应变量是碳纤维应变量的几十倍,铜基体和碳纤维形变不均匀,导致界面承受较大应力,且界面应力随载荷增加而持续增加。在界面应力低于初始损伤条件时,端部界面不发生损伤,界面实现有效的应力传递,应力更多地分布在碳纤维上,同时不同位置的基体先后进入塑性硬化阶段,使得复合材料呈现出硬化现象。当界面应力达到定义的初始损伤应力时,界面开始损伤。随后界面损伤逐渐增大,直到损伤变量=1时,界面完全失效,表现为界面脱黏。从图4(c)看出,材料的应力集中在纤维尖端附近的界面上,由于CSf/Cu界面是一个极弱界面,因此当复合材料受到应力作用时,界面成为最先被破坏的区域而成为裂纹源。在端部界面撕开后,应力发生重分布,沿纤维轴向的界面应力随即增大,界面开始沿轴向撕开,撕裂界面附近的基体应力松弛。与此同时,纤维端部附近的基体应力也达到初始损伤应力,如图4(d)所示,基体迅速发生破坏,且裂纹尖端仍然存在应力集中,裂纹随载荷增加持续扩展。在几个裂纹连通扩展前,裂纹的萌生和扩展仍需载荷不断增大,在载荷达到最大值时裂纹连通。若该纤维端部出现桥联,裂纹很容易扩展连通,材料随即破坏,发生刚度退化,复合材料完全撕裂,应力−应变曲线终止。

图4 纤维长度为60 μm 的CSf/Cu复合材料拉伸细观状态
(a) Interface failure; (b) Elastic deformation; (c) Initial damage; (d) Damage evolution
3.2 纤维长度对复合材料应力分布的影响
纤维增强复合材料的力学性能与纤维长度密切相关,纤维长度影响应力分布,而应力分布是研究复合材料力学性能的根本性要求。本文采用有限元方法进行分析,研究短碳纤维增强铜复合材料的局部应力场,并分析纤维长度以及弱界面对局部应力场的影响,结果如图5和图6所示。在目前的分析中,纤维与基体的弹性模量差别很大,因此纤维的不连续性只影响纤维端部附近的局部应力场。原因是延展性相对较好的铜基体产生塑性变形,以缓和纤维端部附近的应力 集中。
图5所示为短碳纤维增强铜复合材料拉伸过程中,不同长度纤维的轴向Van Mises应力分布。用/表示纤维的轴向位置(为纤维长度,为各位置到端面的轴向距离),/比值为0和1分别表示两端。从图中看出,碳纤维长度分别为60、100、140 μm的复合材料,在各阶段的纤维轴向应力分布曲线均相似,其中起始损伤阶段、损伤演化阶段的曲线均呈“w”形,即由于材料的不连续性,纤维端部附近存在很高的应力区,纤维中段的载荷从两端向中间逐渐增加,符合COX[19]的剪切滞后理论。与剪切滞后理论不同的是,虽然端部存在高应变并造成界面破坏,但由于基体的连续性,纤维端部的应力不为0,而是高应力区。纤维长度为20 μm时,纤维中段的应力在各个阶段都低于端部应力,这表明纤维几乎没有承载能力,应力分散在基体而不过于集中;纤维长度在60 μm以上时,应力明显集中在纤维附近。
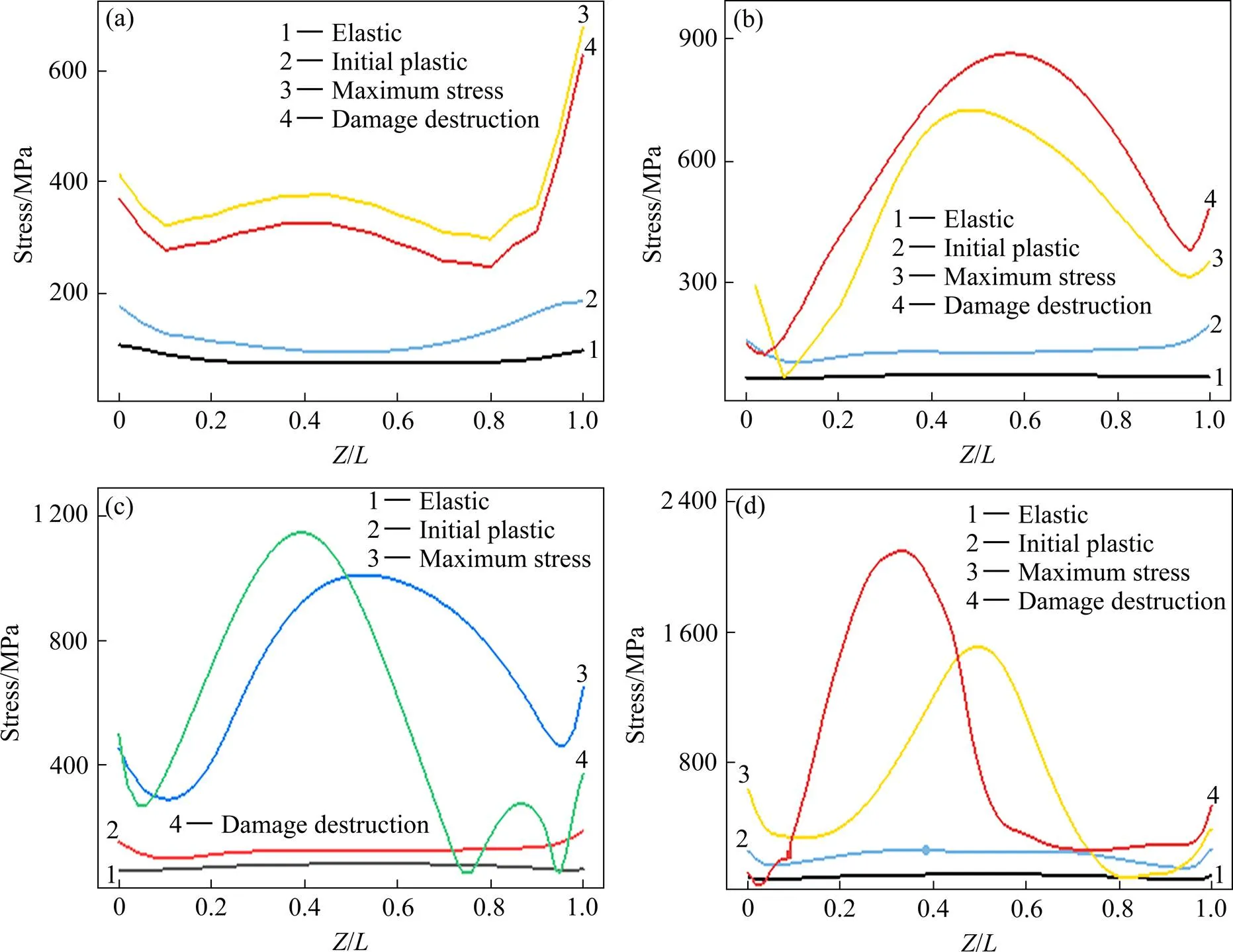
图5 不同长度纤维在CSf/Cu复合材料拉伸各阶段的轴向应力分布
(a) 20 μm; (b) 60 μm; (c) 100 μm; (d) 140 μm
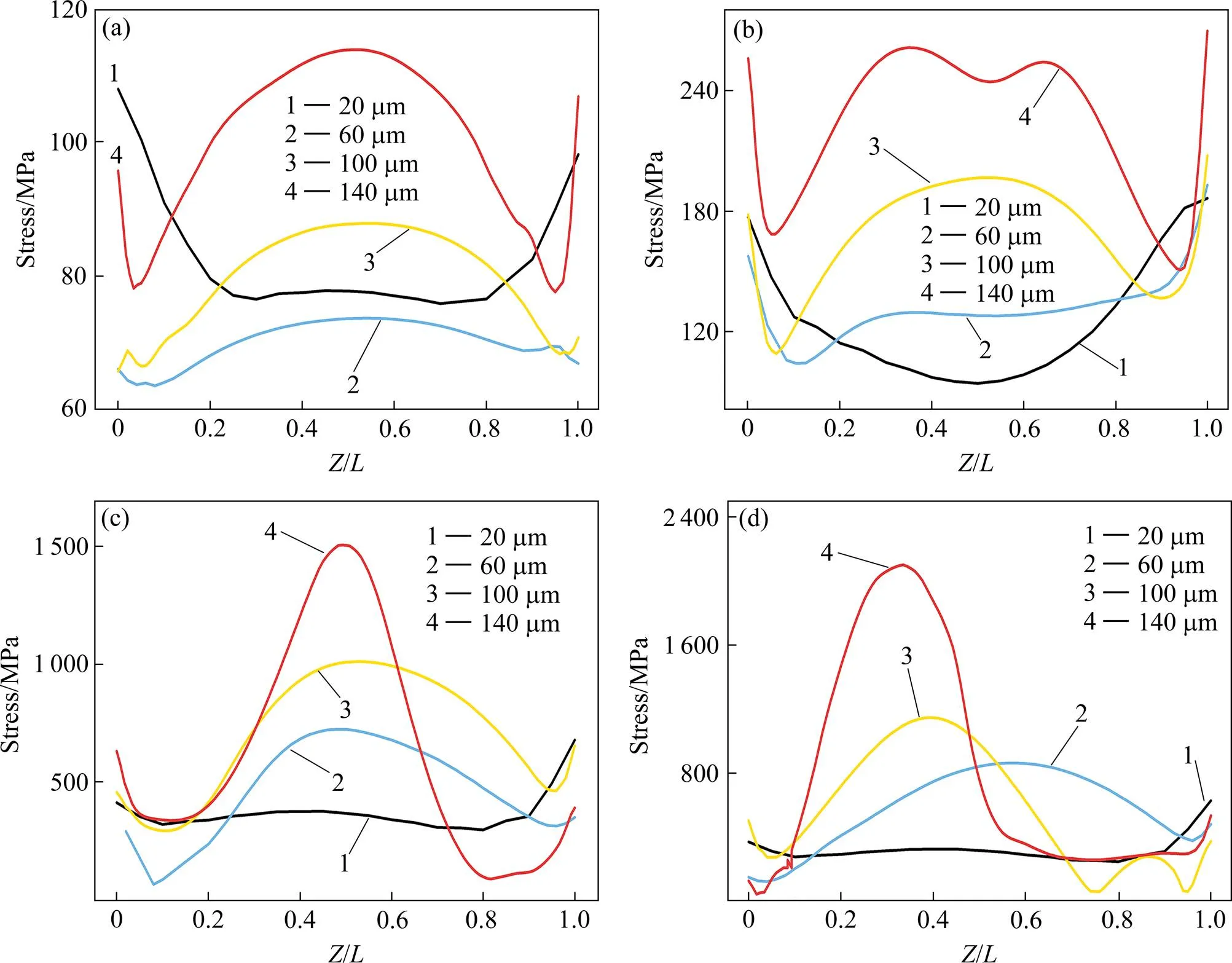
图6 CSf/Cu复合材料拉伸的不同阶段纤维的轴向应力分布
(a) Elastic deformation; (b) Initial plastic deformation; (c) Initial damage; (d) Damage evolution
图6所示为材料拉伸过程中不同阶段的纤维轴向应力分布。在弹性阶段和初始塑性阶段,长度为60 μm以上纤维的轴向应力随平均应力应变水平提高而提高,但应力分布情况基本不变。原因是随变形增加,高正应力区域扩大,但只要端部界面不发生脱黏,应力传递特征就不发生改变。当材料进入损伤阶段后,随应力应变增加,端部的裂纹向中间扩展,造成端部附近界面脱黏,应力传递作用失效,使得应力最大值开始向一侧移动。长度为20 μm的纤维,在弹性阶段和初始塑性阶段,应力主要集中在端部;在损伤和破坏阶段,纤维中段的应力有一定程度的提高,也出现纤维中段的载荷从两端向中间增加,但中段应力的最大值仍远低于端部应力。
3.3 纤维长度对强度的影响
图7所示为不同纤维长度的Csf/Cu复合材料的拉伸性能。由图可知,随纤维长度从20 μm增加到140 μm,复合材料的抗拉强度从146 MPa下降到102 MPa。纤维越长,应力更加集中在纤维附近,纤维附近的界面和基体的应力都增大,造成界面破坏,出现微小裂纹,微裂纹的尖端造成尖端基体应力进一步集中,使得材料更容易被破坏,强度降低。
4 结论
1) 根据拉伸应力−应变曲线,将短碳纤维增强铜复合材料(Csf/Cu)的拉伸过程分为4个阶段:弹性阶段、塑性硬化阶段、起始损伤阶段和损伤演化阶段。随载荷增加,损伤出现在纤维端部的界面和基体上,随后分别向轴向界面和基体演化,裂纹连通后材料刚度完全退化。
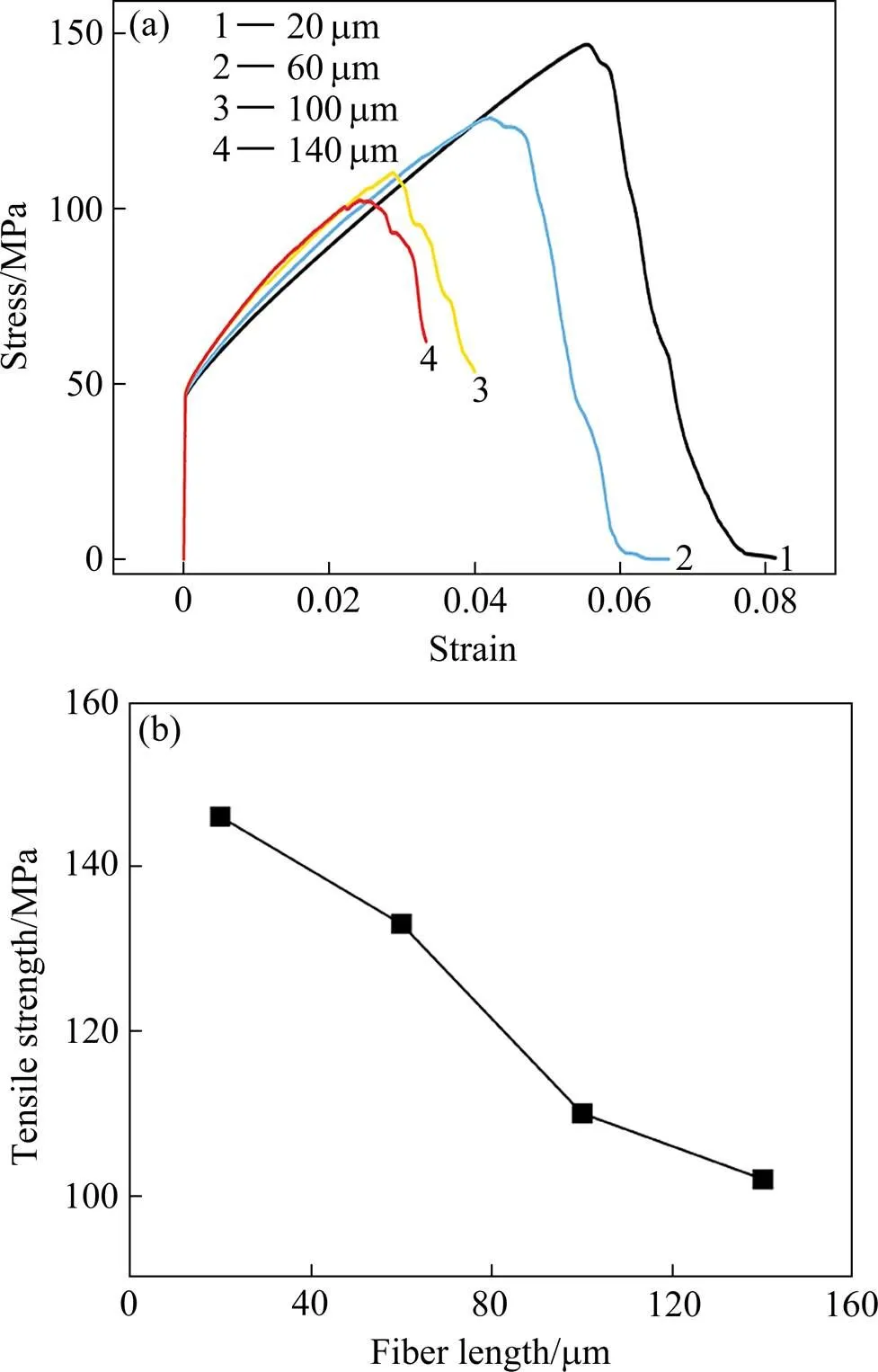
图7 不同纤维长度的CSf/Cu复合材料拉伸性能
(a) Stress-strain curves;(b) Relationship between tensile strength and fiber length
2) 短碳纤维的长度大于60 μm时,纤维的轴向应力分布呈“w”形,即在纤维端部附近存在很高的应力区,纤维中段的载荷从两端向中间逐渐增加。纤维长度为20 μm时,纤维中段的应力在各个阶段都低于端部应力,纤维几乎没有承载能力。
3) 随纤维长度从20 μm增加到140 μm,CSf/Cu复合材料的抗拉强度从146 MPa下降到102 MPa。纤维越长,对材料的强化作用越好,应力更加集中在纤维附近的界面和基体上,导致材料更容易破坏,强度降低。
[1] ZC A, HCF A, JMZ A, et al. Effect of carbon type and morphology on the microstructure and properties of carbon/ copper composites[J]. Wear, 29(5): 460−461.
[2] LANCIONI G, ALESSI R. Modeling micro-cracking and failure in short fiber-reinforced composites[J]. Journal of the Mechanics and Physics of Solids, 2019, 137: 103854.
[3] PIKE M, HICKMAN M, OSKAY C. Interactions between multiple enrichments in extended finite element analysis of short fiber reinforced composites[J]. International Journal for Multiscale Computational Engineering, 2015, 13(6): 83−87.
[4] PIKE M G, OSKAY C. Modeling random short nanofiber-and microfiber-reinforced composites using the extended finite- element method[J]. Journal of Nanomechanics & Micromechanics, 2014, 5(1): 1−11.
[5] PIKE M G, OSKAY C. Three dimensional modeling of short fiber reinforced composites with the extended finite element method [J]. Journal of Engineering Mechanics, 2019, 142(11): 1−12.
[6] YAVAS D, ZHANG Z, LIU Q, et al. Interlaminar shear behavior of continuous and short carbon fiber reinforced polymer composites fabricated by additive manufacturing[J]. Composites Part B: Engineering, 2020, 204: 1−26.
[7] MONDALI M, ABEDIAN A. An analytical model for stress analysis of short fiber composites in power law creep matrix[J]. International Journal of Non-Linear Mechanics, 2013, 57: 39− 49.
[8] GAO J, YANG X, HUANG L H. Numerical prediction of mechanical properties of rubber composites reinforced by aramid fiber under large deformation[J]. Composite Structures, 2018, 201: 29−37.
[9] TIAN J, ZHONG S Y, SHI Z Q. Finite element analysis of creep behavior of AZ91D magnesium matrix composites reinforced with aluminum silicate short fibers[J]. Advanced Materials Research, 2012, 568(11): 311−314.
[10] YANG Q S, QIN Q H. Fiber interactions and effective elasto- plastic properties of short-fiber composites[J]. Composite Structures, 2001, 54(4): 523−528.
[11] HARPER L T, QIAN C, TURNER T A, et al. Representative volume elements for discontinuous carbon fibre composites. Part 1: boundary conditions[J]. Composites Science and Technology, 2012, 72(2): 225−234.
[12] HARPER L T, QIAN C, TURNER T A, et al. Representative volume elements for discontinuous carbon fibre composites. Part 2: determining the critical size[J]. Composites Science and Technology, 2012, 72(2): 204−210.
[13] DEMIRAL M, TANABI H, SABUNCUOGLU B. Experimental and numerical investigation of transverse shear behavior of glass-fibre composites with embedded vascular channel[J]. Composite Structures, 2020, 252(2): 1−28.
[14] LECLERC W, KARAMLAN-SURVILLE P, VIVET A. Influence of morphological parameters of a 2D random short fibre composite on its effective elastic properties[J]. Mechanics & Industry, 2013, 14(5): 361−365.
[15] XIANG L, BAI Y, ALGARNI M, et al. Study on the strengthening mechanisms of Cu/CNT nano-composites[J]. Materials Science & Engineering A, 2015, 645: 347−356.
[16] REDDY B, NARAYANA K B. A comparative study of analytical and numerical evaluation of elastic properties of short fiber composites[J]. IOP Conference Series: Materials Science and Engineering, 2016, 149: 012089.
[17] LEI Y, YAN Y, LIU Y, et al. Microscopic failure mechanisms of fiber-reinforced polymer composites under transverse tension and compression[J]. Composites Science & Technology, 2012, 72(15): 1818−1825.
[18] YU T, TENG J G, WONG Y L, et al. Finite element modeling of confined concrete-I: Drucker–Prager type plasticity model[J]. Engineering Structures, 2010, 32(3): 665−679.
[19] COX H L. The elasticity and strength of paper and other fibrous materials[J]. British Journal of Applied Physics, 1951, 3(3): 72−73.
Computational meso-mechanical model and mechanical property of short carbon fiber reinforced copper matrix composites
HE Donglang, FANG Huachan, LI Yuxing, LI Jinwei
(State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China)
For the short carbon fiber reinforced copper matrix composites (CSf/Cu) prepared by powder metallurgy, a model was established to analyze the tensile damage evolution, fracture mechanical behavior and the influence of weak interface on mechanical properties of composites. The results show that the composites can be divided into elastic stage, plastic hardening stage, damage initiation stage, and damage evolution stage. The stress concentration at the fiber end causes the debonding of the end interface, the damage evolution of the axial interface and the fiber bridging. The damage of the matrix and the accompanying interface are the main fracture mechanism of the material. When the fiber length is greater than 60 μm, the axial stress of the fiber presents a “w” shape, and the fiber has a strong bearing capacity. When the fiber length is 20 μm, the fiber has almost no bearing capacity. The higher the load on the fiber, the easier it is to cause interfacial damage. With increasing fiber length from 20 μm to 140 μm, the strength of the composite decreases from 146 MPa to 102 MPa.
short fibers; copper matrix composites; meso-mechanics; finite element; cohesive element
10.19976/j.cnki.43-1448/TF.2022016
TF125
A
1673-0224(2022)04-382-07
国家自然科学基金资助项目(51501228);中南大学大型仪器设备开放共享基金资助项目(CSUZC202109);中南大学研究生自主探索创新项目(1053320192757)
2022−03−08;
2022−04−20
方华婵,副教授,博士。电话:0731-88836104;E-mail: fanghc@csu.edu.cn
(编辑 汤金芝)
