基于改进模糊参数估计的R-L运动图像复原算法研究

怀国威，罗回彬，张 振，李尚银

（北京理工大学珠海学院，珠海 519000）

0 引言

在道路交通监控及日常摄影等场景摄取图像时，由于摄像设备与目标对象之间存在相对运动，往往会造成得到的数字图像存在模糊的情况。运动模糊图像由于信息特征缺失，不利于细节特征提取和图像辨别，因此，需要通过一定的技术手段对模糊图像进行复原处理。其中，文献［1］利用Radon变换和维纳滤波对模糊图像进行处理，能有效区分图像模糊元素和原信息，但对于带有噪声的图像复原效果不稳定；文献［2］提出了局部模糊目标提取恢复模块以及人工反馈模块融合的方法，复原效果较好，但其计算量较大，且人工成本较高；文献［3］利用一阶差分自相关来识别运动模糊尺度并进行复原，当图像存在噪声的干扰时误差较大，其所能估计的模糊尺度范围较小；文献［4］提出的算法中，噪声常常会较大幅度地干扰倒谱信息的准确识别和正确提取，进而影响其对PSF函数（Point spread function）参数值的正确估计；文献［5］结合四元数小波变换等方法理论模型来进行运动模糊图像的纹理分类，该算法能够较好地适用于不同尺寸大小的模糊图像估计，但是其估计小尺度运动模糊图像的方向时，精确度不高。

本文通过分析噪声对运动模糊图像的影响，分别从三个模块对图像进行处理得到复原图像。第一个模块对数据进行预处理，得到质量较好的图像的倒谱域；第二个模块在倒谱域中估计运动模糊角度和运动模糊尺度；在得到运动模糊参数值后，在第三个模块中构建PSF函数，并使用Richardson-Lucy算法对其进行迭代，得到复原的图像。实验对比显示，本文所提出的改进算法可以适用于一个较大的模糊尺度估计范围，能够较为准确地识别参数、计算量小及对抗噪声能力较强。

1 运动模糊图像工作原理

1.1 运动模糊图像退化模型基本原理

图像复原的关键就是对于退化模型的确定，当模糊系统是空间线性移动不变系统时，考虑噪声因素，图像的退化模型一般可以用公式（1）表达［6-7］。简单来说，即原始（清晰）图像f(x,y)与退化函数h(x,y)进行线性卷积运算后，在噪声n(x,y)干扰下得到的输出为运动（模糊）图像g(x,y)。因此，原始（清晰）图像复原是公式（1）的逆过程，其关键步骤是对退化函数模糊系数的精确估计以及减小随机噪声对图像复原的干扰。

1.2 基于倒谱法的运动模糊参数计算

根据图像卷积定理可知，式（1）中图像卷积运算可以通过傅里叶变换到频域中，将空域中的卷积简化为频域的乘积，减少运算的复杂性，然后再计算傅里叶逆变换，得到倒频谱图来进行后续求解［4］。此外，从图1的图像退化模型分析可知，对于运动模糊图像的复原，需要点扩散函数（PSF）的两个重要参数：模糊方向和模糊尺度。模糊尺度指整张图像全局移动的像素数，而模糊方向是运动的方向与水平方向所成的夹角。

1.2.1 模糊角度估计

由倒谱特性可知，在估计运动模糊图像中的模糊角度时，只要先确定倒谱中条纹方向就基本上确定了运动模糊方向，因此，求解模糊角度最重要的一步就是确定倒谱图中条纹的方向。其具体过程如图2所示。图2（a）是一张运动模糊角度为40°的图像，经过傅里叶逆变换后进行倒谱运算，再压缩居中，得到结果如图2（b）所示，从中能够发现各条纹都是以中央条纹为几何中心，呈现出渐弱、对称的分布，但是由于在图中还有其它干扰特征。通过canny算子对图2（b）进行二值化和Radon变换，将其转换为如图2（c）所示的具有多条规律的亮条纹。至此，对图2（c）取其角度的极大值即可得到运动模糊角度［8］。

1.2.2 模糊尺度估计

对于运动模糊图像，倒频谱三维图能够反映出该图像所固有的两个特性：原始特性和模糊特性。其中，低幅值的成分可以很好地反映出模糊系统特征。同时，通过模糊尺度的值是不同负峰值点间距的一半的特性可以计算模糊尺度的值［9］。如图3所示，为了便于观察计算，可以将运动模糊图像倒谱中心点校准到零点处。假设左边负峰值点为Tgl(k1,m1)，右边负峰值点为Tgr(k2,m2)，则模糊尺度d的计算公式为

1.3 R-L复原算法

对于以上图像，本文假设其呈现泊松分布，通过使用最大似然算法对图像进行迭代，图像会收敛，最终得到一张较为清晰的图像。其迭代复原过程如式（3）所示：

由上式可知，在整个迭代过程中，噪声会随着迭代轮数的增加而进一步扩大，从而影响图像复原的质量。

2 提出的算法

2.1 算法集成设计

整个算法流程图主要分为三个模块。第一个模块为图像的预处理，将图像映射到倒谱域中；第二个模块是在倒谱域中进行运动模糊参数的估计；第三个模块通过估计的模糊参数构建PSF函数，并使用R-L算法迭代得到复原图像。本文提出的算法结构图如图4所示。

2.2 运动模糊图像预处理优化

本文在估计模糊参数前，先分别对图像做灰度化处理和二维傅里叶变换，并计算其此时对数值，平方再经过反傅里叶变换后获得图像的倒频谱。缩小倒频谱的动态范围并对其循环移位，使其可以将低频的频谱成分居中，之后在倒谱域中完成模糊参数的估计。

2.3 改进的倒谱法运动模糊参数及R-L复原算法设计

本文对模糊图像的参数估计方法提出改进，在估计模糊角度时，提出不直接进行Radon变换，而是先通过边缘检测后进行二值化处理，再进行Radon变换（1°～180°），可以直接得到一个极大值序列，序列中的最大值就是所需要的模糊角度值，这样可以比直接对频谱进行Radon变换更加有利于突出极值点，且能够在模糊尺度较小时保证角度估计的准确性。在估计运动模糊的模糊尺度时，本文直接采用一阶差分和自相关算法得到自相关曲线。利用运动模糊尺度是两个共轭相关峰间距的二分之一这一特性，即可得到模糊尺度值，同时，本文还通过实验发现了左右负峰值的对称特性，可以利用该特性只计算一端的值，进而减少50%的计算量。

最终，通过本文提出的改进的模糊参数估计算法得到PSF函数，再使用Richardson-Lucy算法进行迭代收敛，得到最终复原图像。

3 实验结果

本研究在Intel-i7-11700K硬件上进行，选用经典的图像数据集Lena和Sara，在Windows的Matlab环境下完成以下实验分析。

3.1 运动模糊参数实验效果分析

通过对实验结果表1的分析可知，当模糊尺度的值小于30像素时，虽然对于模糊角度的数值预测有较大的误差，但是对于模糊尺度的影响很小。当模糊尺度大于30但不超过100像素时，本算法预测的模糊尺度平均误差不超过5像素，模糊角度平均误差不超过0.5°；当模糊尺度大于100像素时，其模糊尺度会出现较大的误差，但是模糊角度误差很小。如表2所示，相比于其它方法，本文提出的算法的适应范围更广（鉴别范围：30≤L≤100），模糊角度的最大鉴别误差最小，仅为0.17°，整体鲁棒性更强。

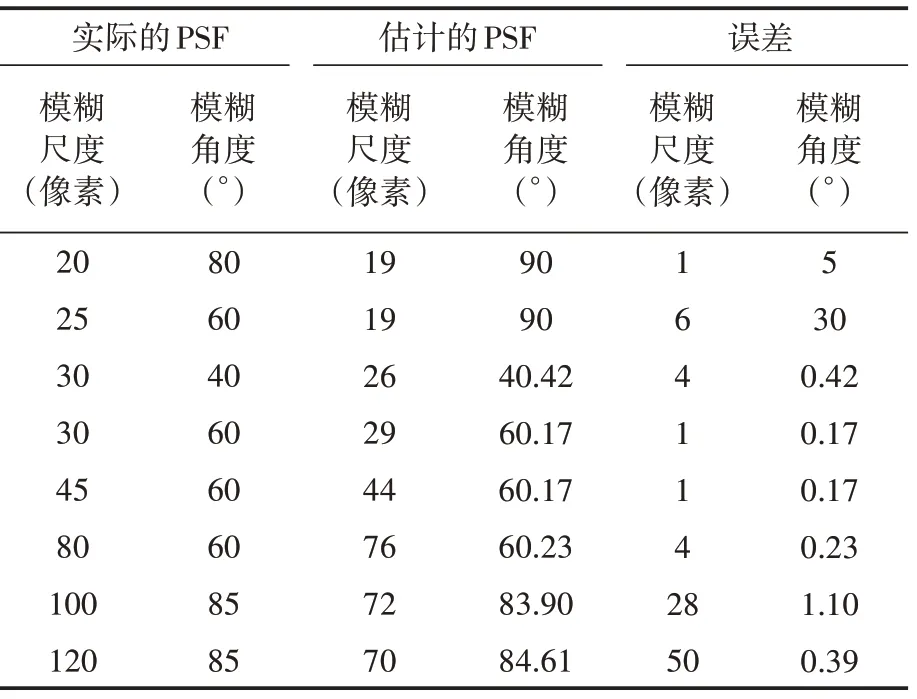
表1 本文提出的运动模糊参数估值

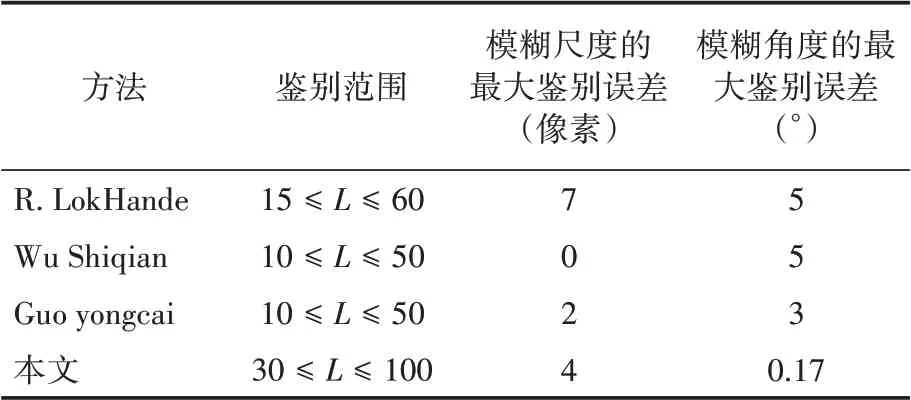
表2 本文的参数估计算法与其它算法对比

3.2 基于改进的模糊参数估计算法复原效果

通过仿真实验可以得到模糊角度为40°，模糊尺度为40个像素的图像，分别进行基于一般倒谱域参数估计（直接通过Radon变换和频谱三维图的参数估计）的R-L算法和本文提出的基于改进的模糊参数估计的R-L算法对模糊图像进行复原，对比实验效果，如图6所示。其中，第一行图像为一般算法迭代效果图，第二行图像为本文提出算法的迭代效果图。

由图6的实验效果可知，本文基于改进的模糊参数估计的R-L算法相比于一般算法在迭代时更先达到较好的图像恢复效果。从视觉上来分析，图6中本文算法的第5次迭代效果略低于一般算法的第10次迭代效果；但是本文算法的第8次迭代效果明显优于一般算法的第10次、第20次的迭代效果，细节纹理特征更加明显，更早地达到收敛效果。

不同算法的最优效果如图7所示，通过观察图7可知，本文方法优于其它算法，能有效抑制振铃效应。考虑到人类自身的视觉系统具有较强主观性，人眼判断时会存在主观误差。所以，为了更加客观真实准确地分析评价图像质量，本文采用以下三个指标：均方根误差（MSE）、峰值信号比（PSNR）、灰度平均梯度（GMG）。峰值信号比和灰度平均梯度的值越大，表示图像复原的质量越好；均方根误差值越小，则表示图像质量越好［10］。

通过表3可知，本文提出的算法在对比实验所得到的评价指标中，都取得了较好结果。其中Lena.png中，虽然MSE值与其它算法的最优MSE值相差1.639，但其PSNR和GMG值都优于其它算法；Sara.png中实验结果显示，本文所提算法的三个指标都优于其它三个算法。因此，本文提出的算法在定性和定量评价上都有较好的效果，且该算法的稳定性高。

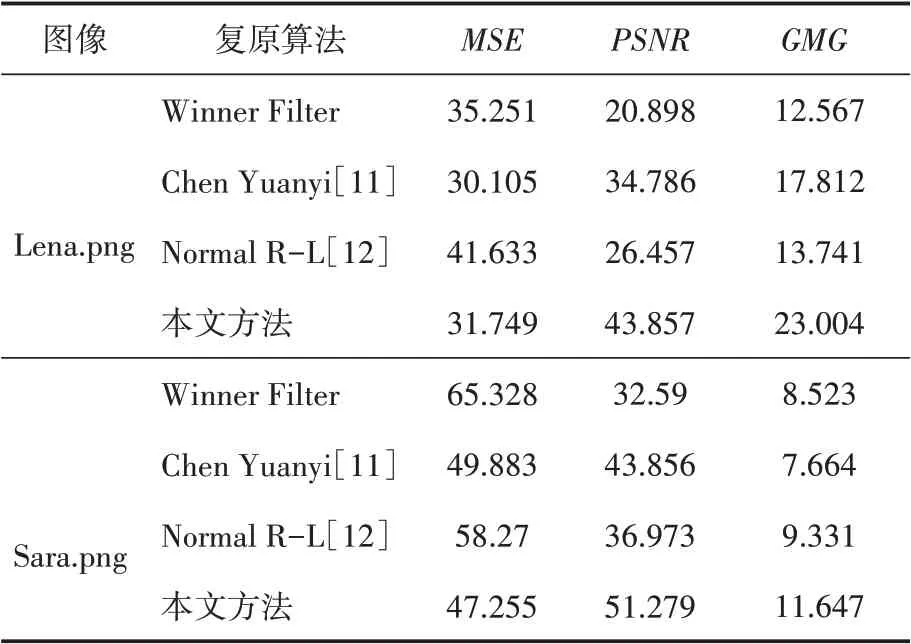
表3 本文算法与其它算法评价指标对比

4 结语

对于运动模糊参数的精确估计是保证图像复原质量的前提。本文通过先对图像进行预处理，分析研究图像的频谱及倒谱的特性，提出改进的参数估计方法：在估计模糊参数的过程中，使用边缘检测得到条纹突出的新倒谱图，再通过对其进行Radon变化计算来估计模糊方向；在估计模糊尺度时，以一阶差分及自相关方法确定自相关曲线，通过共轭峰特性确定模糊尺度值。最后构建一个新的PSF函数并代入到Richardson-Lucy算法中进行迭代。实验结果进一步表明，本文提出的基于改进模糊参数估计的图像复原算法可以更容易收敛，计算更加简单，并且其复原效果显示本文所提算法有较强的鲁棒性，对图像恢复技术及其他相关领域研究有较大作用，有望为相关退化图像的恢复提供更好的研究基础。同时，使用此类算法在实际生活中也有极广的应用范围，比如当监控拍摄到肇事而逃的司机时，可能由于相对运动导致所拍摄的犯罪人的车辆、车牌有一定程度的运动模糊，使用此类图像去模糊算法可以加快破案的速度，对实际生活有非常重要的意义。