基于APSO_ELM算法的地铁列车碳滑板磨耗的预测

郝玉然，王自鑫，李正培

（郑州地铁集团有限公司，郑州 450000）

0 引言

作为一个连接地铁列车和接触网的重要装置，受电弓被安装在地铁车顶［1］。其性能对保证地铁具有稳定的电流具有十分重要的作用［2-4］，在地铁运行过程中，碳滑板和接触网之间产生相对摩擦，这种摩擦一旦对受电弓滑板造成严重损伤便会产生受电弓卡网或拉网故障，严重时将导致地铁电压不稳定，进而导致地铁停运。因此，在日常电客车检修作业过程中，对碳滑板的厚度测量周期为半月。目前国内外针对碳滑板磨耗的研究主要集中在两个方面：①研究如何准确检测出碳滑板的厚度，以保证地铁列车的安全运营；②研究弓网之间的振动，采取一些主动控制策略减小振动，进而减小碳滑板的磨耗量。

受电弓滑板磨耗的检测手段有接触测量法［5-7］、激光检测法［8-11］、超声波检测法［12］、图像处理检测法［13］。图像处理检测法作为一种新型技术手段，已被广泛应用于碳滑板磨耗检测中［14］。随着新时代科学技术的不断发展，人工智能手段逐渐被应用于地铁车辆磨耗部件的预测。地铁列车的各个部件在每日的不断运行中逐渐被磨损，对这些磨损件进行预测以保证车辆的安全运行尤为重要。现有对地铁车辆磨损件的预测研究包括车轮踏面磨耗、闸瓦磨耗和钢轨磨耗的预测［15］。

本文以受电弓碳滑板磨耗为研究对象，利用日常积累的受电弓碳滑板人工测量数据，通过极限学习机（extreme learning machine，ELM）对碳滑板磨耗量进行预测。针对极限学习机随机初始化权值和阈值导致模型泛化能力差的缺点，使用引入收缩因子的自适应粒子群算法（adaptive particle swarm optimization，APSO）对权值和阈值进行优化，得到一种预测精度更高的APSO-ELM碳滑板磨耗预测模型。

1 极限学习机

2005年，Huang等人提出了极限学习机ELM，它是在前馈神经网络基础上改进的一种新的机器学习算法［16］。该算法具有训练速度快、设置参数少、准确率高的特点，同时具有较强的泛化性能。该模型与人工神经网络一样，都包含有输入层、隐含层和输出层。不同之处在于，在ELM模型训练过程中通过设置隐含层层数，根据最小二乘法计算输出权值和阈值就能完成对模型的训练［17］。ELM模型示意图如图1所示。

当ELM模型中有N个样本（Xi，Yi）时，Xi=表 示 样 本 输 入，Yi=表示样本输出，则单隐含层前馈神经模型的输出为

式（1）中，K代表隐含层神经元个数；g（x）代表隐含层神经元激活函数；Wi=[wi1,wi2,wi3,…,wim]T代表隐含层和输入层的权值；Bi=[bi1,bi2,bi3,…,bim]T代表隐含层和输入层的阈值；βi=[βi1,βi2,βi3,…,βim]T代表隐含层和输出层的权值。单隐含层神经网络预测的目标是保证预测值与实际值的误差最小，即以零误差逼近样本输出，预测值与实际值的误差为

即存在βi、Wi和Bi使下式成立。

式（3）矩阵形式可表示为

式（4）中，H表示隐含层输出矩阵；β表示输出权值；T表示样本期望输出。当ELM模型中隐含层激励函数g（x）无限可微时，输入权值W和隐含层阈值B随机初始化，输出权值β通过最小二乘法计算得出，该函数的最小范数为：

式（5）中，H+为隐含层输出矩阵H的Moore-Penrose的广义逆。

2 自适应粒子群算法（APSO）

2.1 粒子群算法

1995年，Kennedy和Eberhart模拟鱼群和鸟类在自然界中的群聚行为，提出了粒子群算法（particle swarm optimization，PSO）［18］。该算法与人工鱼群算法和蚁群算法相同，都模拟物种群体智能行为。

粒子群算法通过在算法迭代过程中不断调整个体的位置对目标函数进行空间寻优，算法初始阶段以随机的形式初始化种群中个体位置。粒子的位置由随机性部分和确定性部分两部分组成。每个粒子位置受当前全局最优位置g*和它的历史最优位置影响，粒子的移动也具有随机性。

在PSO算法中，算法初始阶段在d维目标空间中随机生成一群粒子表示目标函数的解，每个粒子i的位置向量为速度向量为，每个粒子的速度和位置在变量范围内随机初始化。在PSO算法迭代过程中，粒子i在d维空间上的速度和位置更新公式为

式（6）中，ω表示惯性体重；c1和c2表示加速度系数；rand1和rand2是两个独立均匀分布在［0,1］之间的随机数；pBest表示个体最优位置；nBest表示种群最优位置。在算法迭代过程中为了防止个体位置超出目标函数变量空间，设置粒子的位置范围为[xmin,xmax]，速度范围为[vmin,vmax]。xmin和xmax的值根据目标函数确定，vmin和vmax的值根据xmin和xmax确定。

2.2 自适应粒子群算法（APSO）

自适应粒子群算法在粒子群算法中引入收缩因子来对PSO算法进一步收敛以改善PSO算法的性能，即将式（6）修改为

式（8）中χ为收缩因子，可表示为

当χ设置为0.729，有

将c1和c2都设置为2.05。从数学上讲，收缩系数等于惯性权重。

3 APSO-ELM预测模型与模型评价指标

3.1 APSO-ELM预测模型步骤

（1）选择模型输入数据和输出数据。根据碳滑板磨耗选择合适的影响因子，本文选择影响碳滑板磨耗的主要因子——列车运行公里数，作为模型的输入，选择碳滑板厚度作为模型的输出；

（2）样本数据分为训练数据和预测数据，为了进一步提高预测效果，对训练数据和预测数据进行归一化处理；

（3）根据样本数据特点选择合适的ELM模型输入层、隐含层和输出层神经元个数，并选择不同的激活函数测试模型预测效果，最终选择合适的激活函数；

（4）对ELM模型进行训练。选择ELM模型的均方误差MSE作为APSO算法中粒子的适应度函数，通过MSE值得到个体最佳pBest和全局最优值gBest；

（5）根据式（8）和式（7）更新粒子速度和位置，并判断个体速度和位置是否超出解空间；

（6）根据APSO算法确定的ELM模型的权值和阈值，得到APSO算法优化后的ELM模型，将预测数据输入模型得到预测结果；

（7）通过模型评价指标对碳滑板磨耗的APSO-ELM预测模型进行有效性和精确性评价。

3.2 模型评价指标

为更准确地评价APSO-ELM预测模型的有效性，本文选用平均绝对百分比误差（mean absolute percentage error，MAPE）、均 方 根 误 差（root-mean-square error，RMSE）和希尔不等系数（theilinequality coefficient，TIC）3个评价指标对预测模型进行分析。评价指标值越小，则该模型预测性能更优。MAPE、RMSE和TIC的计算公式分别为：

上述三式中，yi表示人工测量的碳滑板厚度；y'i表示APSO-ELM模型预测的碳滑板厚度；n为预测样本数目。

4 碳滑板磨耗预测分析

在MATLAB 2016b的环境下，将实验数据分为测试集和预测集，并完成对ELM模型和APSO-ELM模型的训练并测试预测结果，通过模型评价指标对其预测效果进行评价。确定模型参数前通过设置不同参数比较预测效果，最终确定APSO-ELM模型和ELM模型的模型参数。当输入层神经元个数为1，隐含层神经元个数为30，输出神经元个数为1，隐含层激活函数选择sigmoid函数时能够取得较好的预测结果。APSO-ELM模型中种群规模为50，最大迭代次数T为200，学习因子为c1=c2=2.05。

本文选择的数据来自2020年郑州地铁车辆的碳滑板人工测量厚度数据，具有一定的真实性。数据集中有270组数据，仿真时选择235组数据作为训练集，35组数据作为测试集。

为了证明APSO-ELM模型能够取得较好的预测效果，选择其预测结果与ELM模型预测结果进行对比，预测结果如图2和图3所示。由图2和图3可知，APSO-ELM模型预测值更贴近真实值，说明APSO-ELM模型预测精度远远优于ELM模型，也说明使用APSO算法对ELM模型权值和阈值进行优化，能够提高ELM模型的预测精度。图4为APSO-ELM模型在迭代过程中的适应度函数曲线。APSO-ELM模型和ELM模型的评价指标MAPE、RMSE和TIC值如表1所示。由表1可知，APSO-ELM模型的评价指标值均比ELM模型小。综合以上可以看出，APSOELM模型预测精度高，在地铁列车碳滑板磨耗预测中具有一定的准确性和有效性。

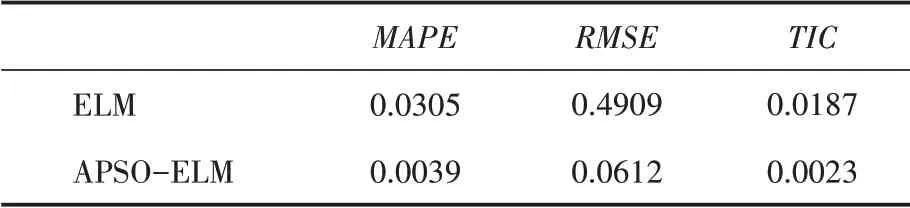
表1 不同模型的评价指标值

5 结语

本文在PSO算法的基础上，引入收缩因子得到APSO算法，以改进PSO算法全局搜索能力和提高收敛速度。针对ELM随机初始化权值和阈值的缺点，使用APSO算法优化ELM模型权值和阈值，进而提出一种APSO-ELM模型并将其应用于碳滑板磨耗预测。通过对比APSOELM模型和ELM模型的预测结果可知，APSOELM模型预测结果更接近实际值。APSO-ELM模型的MAPE、RMSE和TIC值明显比ELM模型小，证明APSO-ELM模型有更强的泛化能力和更高的预测精度。APSO-ELM模型通过对已有数据进行训练，利用训练后的模型对地铁列车受电弓碳滑板磨耗进行预测，能够准确预测出完成该行程后的滑板厚度数据，可进一步减少列车检修作业人员测量误差。将该算法运用于智能运维平台上，能够根据公里数预测出碳滑板厚度是否达到更换的警戒线，从而对碳滑板厚度进行报警。同时也能减少人为测量误差，在一定程度上减少碳滑板的浪费，从而提高碳滑板的利用率，节约地铁车辆运营成本。