3种成分数据方法在24 h活动行为时间使用流行病学研究中的应用比较
2022-12-07谭健怡黄宝莹任志强程金群黄珍惠徐华富李红娟郜艳晖
刘 晴,谭健怡,黄宝莹,任志强,程金群,黄珍惠,徐华富,李红娟,郜艳晖
近年来,身体活动(physical activity,PA)不足(卫文,2018;WHO,2018)、久坐行为(sedentary behavior,SB)增加(郭强 等,2017;Bauman et al.,2011)和睡眠(sleep,SLP)不足(闫静弋 等,2019;Keyes et al.,2015;Sheehan et al.,2019)等不良生活行为越来越普遍,导致肥胖、高血压、心血管疾病和癌症等风险升高,并增加全死因死亡率(于洪军等,2013;周志雄,2015;Carson et al.,2016;Chaput et al.,2016;Patterson et al.,2018;Poi‐tras et al.,2016)。此外,过度的SB和SLP不足还会削弱身体活动带来的健康收益(Cha‐put et al.,2017)。既往研究多从绝对量角度探讨单个活动行为时间的分布特征或其与健康结局的关系,忽略了行为时间的相对大小及内在联系。从连续活动谱(movement continuum)角度来看,中高强度身体活动(moderate-to-vigorous-intensity physical activity,MVPA)、低强度身体活动(light-intensity physical activity,LPA)、SB和SLP构成一天24 h的活动行为,四者所用时间为互斥关系,即24 h内一种行为使用时间的改变,需在其他至少一种行为时间上进行补偿,所导致的健康效应除受该行为时间改变影响外,也部分归因于其他至少一种行为时间的补偿性改变。因此,将各种行为时间看作一个24 h连续谱,从相对量角度研究24 h各种行为时间的分布特征、影响因素以及与健康指标的关系更趋合理,同时对制定24 h各种活动行为时间平衡指南,促使健康效益达到最优化也有重要意义。
目前,PA、SB和SLP的24 h综合研究备受国内外学者关注。Pedišić(2014)认为,要确定 SLP、MVPA、LPA 以及总PA时间对健康的独立贡献,需要在这些变量间相互调整;作为时间使用成分的一部分,需要使用成分数据分析(compositional data analysis,CoDA)方法。宋俊辰等(2020)综述了时间使用流行病学在身体活动领域的应用进展。时间使用流行病学主要研究人群中与健康相关的时间使用模式的分布现状、趋势、决定因素及对健康结局的影响,以达到预防不良的时间使用模式,实现个体健康时间最佳分配的目标。这一概念由 Pedišić等(2017)提出,同时提出的还有时间使用流行病学综合研究框架,时间使用的分布特征位于该研究框架中心位置,最佳时间使用平衡为核心要素,不同的结局可能与不同的时间使用模式有关。因此,准确描述24 h MVPA-LPA-SB-SLP使用时间在人群的分布特征,有助于确定最佳时间使用平衡模型,为制定公共卫生和健康干预策略提供科学可靠的参考和依据。
从统计学角度,24 h活动行为研究除时间绝对量外,也显示了时间使用的相对量信息,对应的各活动行为时间数据存在定和限制(即所有成分比例总和为1),称为成分数据(compositional data)。成分数据样本空间属于标准的单形空间,协方差阵至少有D个元素必为负数,其中D为成分个数(张尧庭,2000;Van den Boogaart et al.,2013)。因此,传统基于欧式空间的经典统计方法并不适用于成分数据。针对成分数据的统计方法最常用的是等距对数比变换(isometric logratio transformation,ilr),即假设成分数据服从加法逻辑正态分布(additive logistic normal,aln),通过ilr将其从单形空间映射到欧式空间,进而基于正态分布采用传统方法分析。现有研究采用ilr方法主要探讨24 h活动行为的各类健康效应,此时24 h活动行为被作为解释变量。但当需要描述24 h活动行为时间使用的分布,或将其作为结局变量时,ilr方法易受异常值影响,可能会严重误导结果。更重要的是,ilr方法得到的参数只能在转换后的空间下解释,没有直接的含义,结果解释不直观。相比于ilr,Dirichlet分布能直接基于成分数据单形空间定义模型,更直观、更有吸引力。该分布具有良好的数学性质和参数易解释等诸多优良性质(Ng et al.,2011),但对于成分间强相关或弱正相关的成分数据适用性较差。鉴于此,Ongaro等(2013)提出Dirichlet的混合分布,即Flexible Dirichlet(FD)模型,既能保留Dirichlet分布的良好数学和成分性质,又可弥补Dirichlet分布不足,具有更大的灵活性。相比于ilr和Dirichlet分布,FD模型更能捕获成分数据的复杂特征(Migliorati et al.,2017a),但目前Dirich‐let或FD方法在24 h使用流行病学研究中仍鲜有应用。本研究详细介绍了3种成分数据方法及其优缺点,并通过实例分析比较3种方法在拟合24 h活动行为时间分布的效果,选择最优方法阐明24 h PA、SB和SLP行为时间使用分布特征。
1 成分数据原理与方法
1.1 成分数据原理
若任意D元向量y=(y1,y2,…,yD)满足以下表达式:
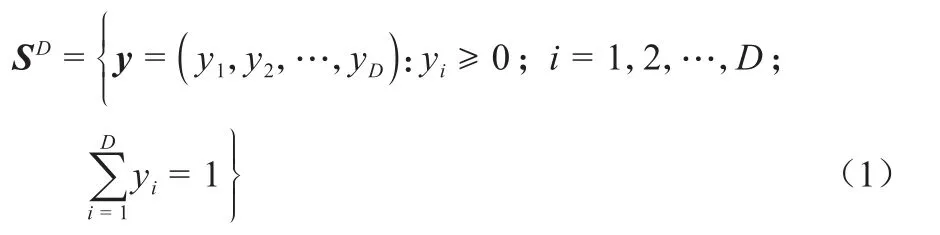
式(1)中,y为D元成分数据,记为y∈SD。D为成分个数;yi为第i个成分,yi对应的取值称为分量,表示i成分所占的比例。
1.2 成分数据方法
1.2.1 ilr方法
ilr方法通过构建标准正交基将成分数据进行对数比转换,以使成分数据从单形空间SD映射到欧式空间RD-1,再用经典统计方法分析。本研究选取最常用的标准正交基,即将感兴趣的成分放在第一位的标准正交基,以捕获该成分的所有相关信息。假设y=(y1,y2,…,yD)∈SD,为D元成分数据,等距对数比转换定义为(Egozcue et al.,2003;Fišerová et al.,2011):
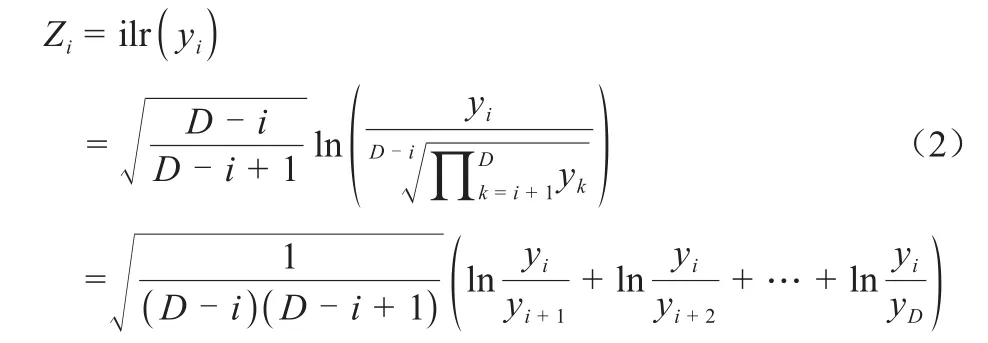
式(2)中,yk为第k个成分,k=i+1,i+2,…,D;i=1,2,…,D-1。ilr将单形空间上的成分数据y=(y1,y2,…,yD)变换为欧式空间上的普通向量Z=(Z1,Z2,…,ZD-1),并假设Z服从多元正态分布,其联合密度函数为:
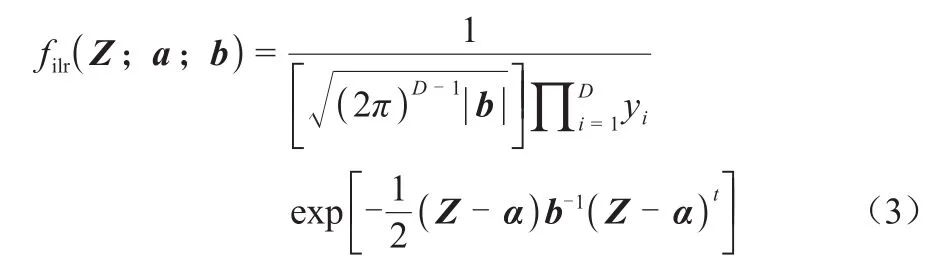
记为Z~filr(Z;a;b)。式(3)中,向量a=(a1,a2,…,ak)为Z均值向量,满足ak=E(Zk);b=(b11,b12,…,bkl)为Z方差协方差阵,满足bkl=Cov(Zk,Zl),k、l=1,2,…,D-1。
似然函数(likelihood function)是指在参数给定条件下观察值的分布。ilr似然函数为:
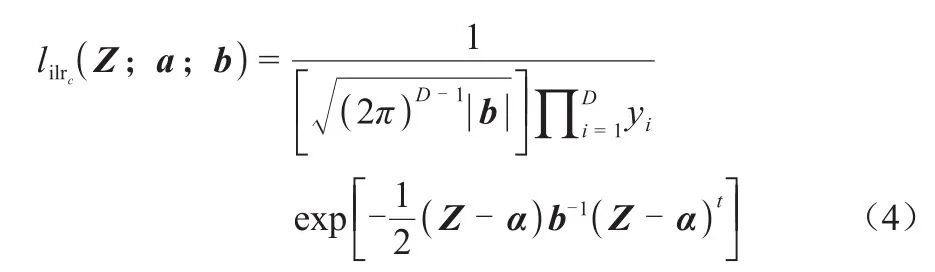
式(4)中符号或字母含义同式(3),c表示已指定参数a和b。
ilr满足尺度缩放性和扰动不变性,根据ilr计算y的均数E(y),可准确描述y的集中趋势。均数E(yi)定义为:

因为单个成分的方差不包含成分间相互依赖的任何信息,而一个成分的变化必然受其他成分变化的影响,因此,成分数据的离散趋势用变异矩阵Τ即成分间对数比方差进行描述,其中变异矩阵元素tij越接近0,相应两个成分对数比方差越小,成分间比例(即共同依赖性)越强。
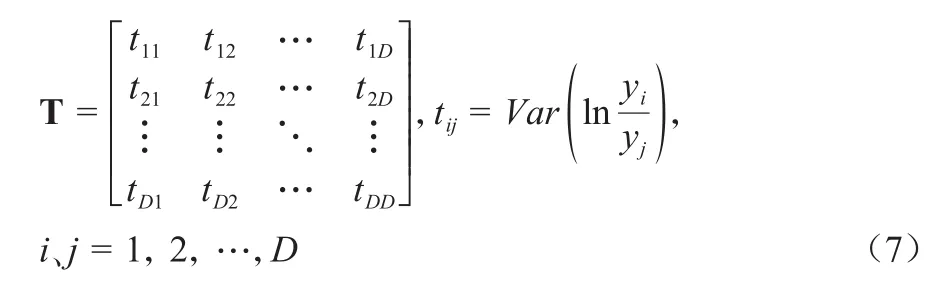
1.2.2 Dirichlet方法
Dirichlet分布是一类在实数域以正单形为支撑集的高维连续概率分布,是Beta分布在高维情形的推广,Beta分布是一个 2维的 Dirichlet分布(Lin,2016;Ng et al.,2011)。假设D元成分数据y=(y1,y2,… ,yD)∈SD服从Dirichlet分布,其密度函数(Lin,2016;Ng et al.,2011)为:

记为y~fD(iry;α)。式(8)中,β为多元的Beta函数;向量α=(α1,α2,…,αD)为无量纲分布参数,满足αi>0;Γ为伽马函数。
Dirichlet似然函数定义为:
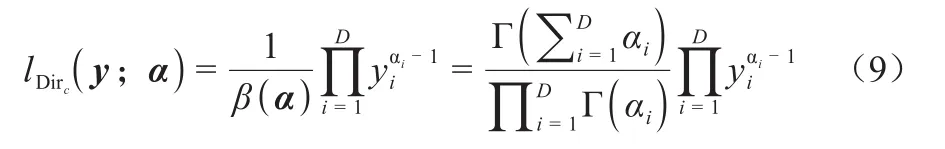
式(9)中符号或字母含义同式(8),c表示已指定参数α。
基于Dirichlet分布计算成分数据各成分的均数E(yi)和标准差σ(yi),可定量描述成分数据各成分的集中趋势和离散趋势:
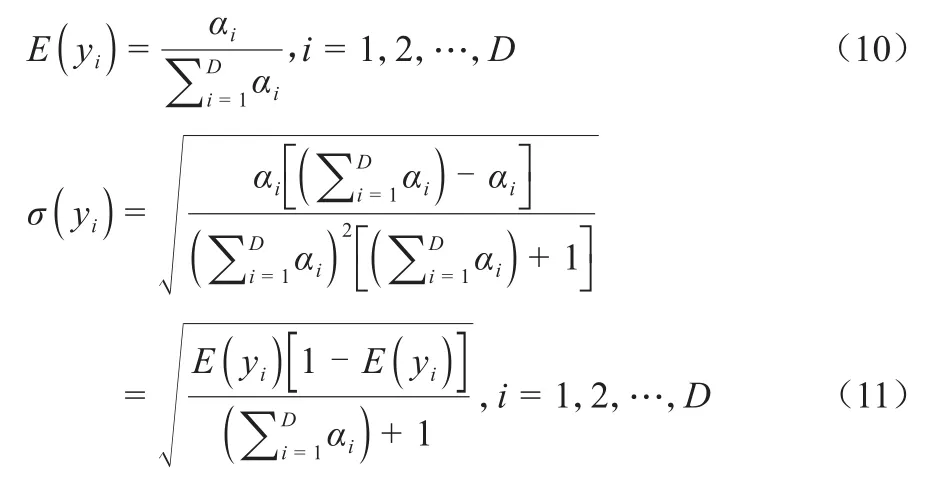
1.2.3 FD方法
FD分布是指从多个独立等比例伽马随机变量基开始,给第i个元素随机分配一个独立的伽马随机变量,构成D维(D>1)正相关随机变量,最后将D维正相关随机变量基归一化处理。假设D元成分数据y=(y1,y2,…,yD)∈SD服从FD分布,FD分布可看作多个Dirichlet分布的有限混合,通过对Dirichlet重新参数化,重新定义均向量结构为单形空间中各成分重心与第i个顶点(i=1,2,…,D)的线性凸组合,构建各成分均向量不同但精度参数相同的Dirichlet混合分布,即FD分布,其密度函数(Migliorati et al.,2017a;Ongaro et al.,2013)为:
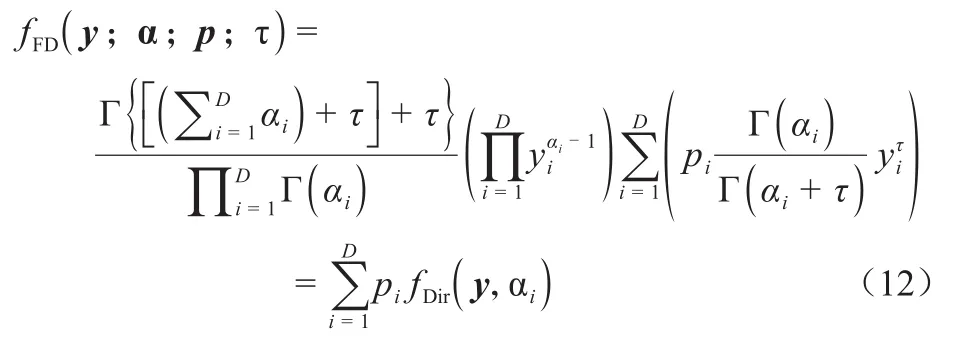
记为y~fF(Dy;α;p;τ)。式(12)中,向量α=(α1,α2,…,αD)为形状参数,满足αi>0。当所有αi<1时,FD分布密度函数为U形,当所有αi=1时,FD分布密度函数为常数,当所有αi>1时,FD分布密度函数为的单峰模式(unimodality);向量p=(p,p,…,12pD)为概率参数,满足,τ越大,第i成分的模式(mode)向单形第i个顶点移动越多;αi=α+τei,ei表示除第i位置取值为1外,其余位置取值为0的向量。Γ为伽马函数。
FD似然函数为:
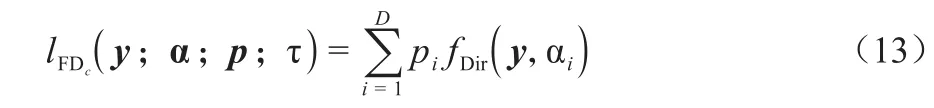
式(13)中符号或字母含义同式(12),c表示已指定参数α、p、τ。但需注意FD为混合结构模型,在估计最大似然函数时作为一个数据缺失问题处理,FD对数似然函数为:
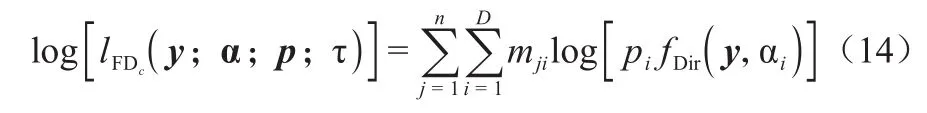
式(14)中,mj=(mj1,mj2,…,mjD)表示缺失数据,取值为0或1,当第j个观测在第i个成分混合模型出现时,mji=1,否则为0。n为样本量;j=1,2,…,n;i=1,2,…,D。其余符号或字母含义同式(12)。FD分布允许多峰模式(multi‐modality),选择合适的αi、pi后,通过增加 τ的值可以达到k峰模式(k≤D)。
基于FD分布计算成分数据各成分的均数E(yi)和标准差σ(yi),可用于描述成分数据各成分的集中趋势和离散趋势:
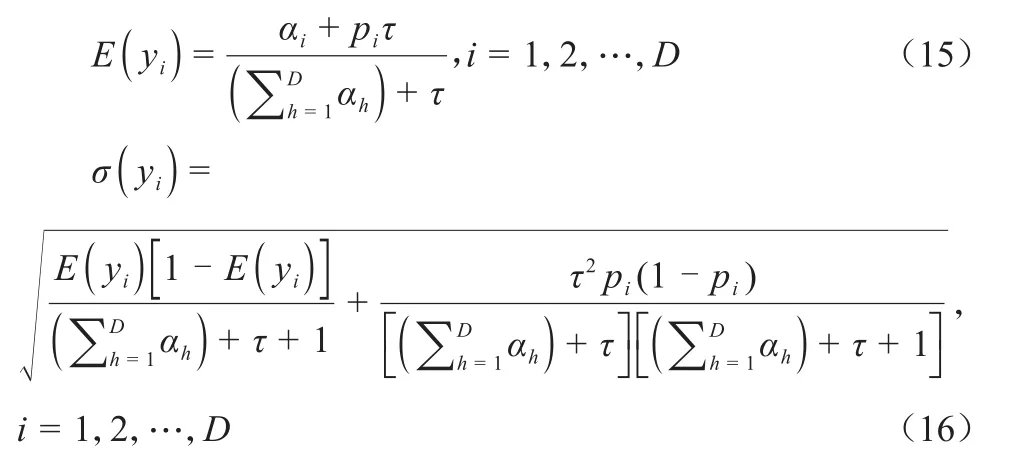
1.2.4 成分数据方法优缺点及差异
上述3种方法存在差异,各有优缺点(Di Brisco et al.,2017;Migliorati et al.,2017a;Ng et al.,2011;Ongaro et al.,2013)(表1)。

表1 3种成分数据方法优缺点及差异Table 1 The Advantages,Disadvantages and Differences of Three Compositional Data Methods
1.2.5 成分数据方法拟合效果评估
用AIC准则(Akaike information criterion,AIC)和BIC准则(Bayesian information criterion,BIC)评价ilr、Dirichlet和FD 3种方法拟合成分数据特征效果,AIC和BIC越小,描述成分数据越准确,拟合效果更好。
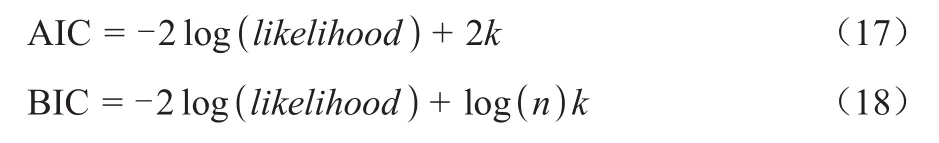
式(17)和(18)中,likelihood为似然函数;k为参数个数;n为样本量。
1.3 成分数据方法的应用
在PubMed和中国知网检索2015年1月—2020年10月的24 h活动行为时间相关研究,英文检索关键词为“24 hour”“physical activity”“compositional data”,中文检索关键词为“身体活动”“行为活动”“24 h行为”“成分数据”。最终共筛选出符合条件的24 h行为时间相关研究文献86篇(英文85篇,中文1篇),包括2018年以前32篇,2019年27篇,2020年26篇。其中,85项研究采用ilr方法将24 h行为活动成分数据视为解释变量,研究其对各类健康结局的影响。研究显示,一天24 h限制条件下,MVPA、LPA、SB或SLP与身体质量指数(Curtis et al.,2020)、体脂率(Pelclová et al.,2020)、脂肪指数(Oviedo-Caro et al.,2020)等肥胖指标、心脏代谢风险评分(Lee et al.,2020;Swindell et al.,2020)、心肺适应性(Oviedo-Caro et al.,2020)以及健康相关的生活质量关联(Curtis et al.,2020),将MVPA时间替换为其他行为(LPA、SB或SLP),将增加肥胖指标和心脏代谢风险、降低心肺适应性以及健康相关的生活质量。此外,增加MVPA也可能使老年人的骨骼健康得到改善(Rodríguez-Gómez et al.,2020)。另一方面,SB与抑郁症状存在正关联,将SB时间分配给MVPA或SLP可缓解抑郁症状(Del Pozo Cruz et al.,2020)。SB与全因死亡率也存在正关联,LPA与全因死亡率负关联,将MVPA或LPA时间替换成SB时间会增加全因死亡率(Von Rosen et al.,2020)。截至2020年10月,仅有1项研究将24 h行为活动成分数据视作结局变量,采用Dirichlet方法分析儿童视屏时间与24 h运动行为之间的关系,结果表明,与2~3岁时每天注视屏幕1 h或更少的儿童相比,2~3岁时每天注视屏幕3 h或更长时间的儿童在5.5岁时表现出更多的SB,较少的MVPA和LPA(Chen et al.,2020)。作为最新提出的成分数据方法,FD理论在24 h时间使用流行病学研究领域中仍未受到关注,但方法学研究和实例结果均表明FD方法的灵活性使其比ilr和Dirichlet方法更能捕获橄榄油或者沉淀物成分的特征(Migliorati et al.,2017a;Ongaro et al.,2013)。因此,采用FD模型将24 h活动行为成分数据视为结局变量并直接拟合,以及基于FD模型聚类进行24 h活动行为模式识别,仍是方法学应用的创新领域,尚需更多的探索。
1.4 成分数据的可视化
与传统数据不同,成分数据中各成分相互约束,可用三元图进行可视化。其中,三元图是各边长度均为1的等边三角形,3个顶点分别表示3个成分。离顶点越远,顶点所在成分的分量越小,反之越大。由点出发向各边零坐标正方向作平行线,平行线与成分所在边的交点到零坐标的距离即为该点在该成分的分量。成分A、B、C所在三角形边分别为ZX、XY、YZ,O点在成分A、B、C的分量分别为ZA=0.4,XB=0.4,YC=0.2(图1)。
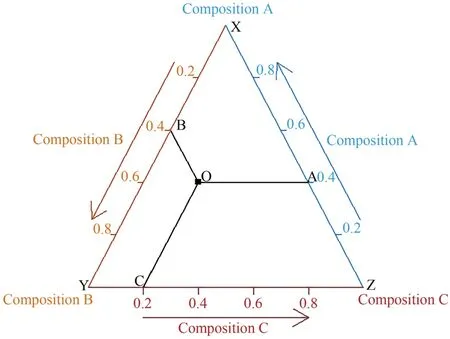
图1 三元图示例Figure 1.An Example of Ternary Graph
成分数据均向量作为一个点描绘在三元图上代表整个成分数据的集中趋势。三元图上的等密度水平线反映成分数据各成分离散程度,且等密度水平线越密集,对应成分离散程度越小,反之越大。
当成分数据中包含3个以上成分时(如MVPA-LPA-SB-SLP),可分别绘制其中3个子成分的三元图。
1.5 统计软件
本研究使用R 3.6.0软件完成,其中,ilr和Dirichlet方法相关 R包为 compositions包(Van den Boogaart et al.,2018),FD方法相关R包为FlexDir包(Migliorati et al.,2017b)。
2 实例分析
2.1 研究对象与方法
本研究实例数据来自2005—2006年美国健康与营养调查(National Health and Nutrition Examination Survey,NHANES)的16~85岁(n=3 682)美国居民日常24 h活动行为,身体活动采用加速度计(ActiGraph AM 7164)测量获得。研究人群中男性1 823人,女性1 859人;青年人(16~44岁)1 859人、中年人(45~59岁)733人、老年人(60~85岁)1 090人。本研究在CoDA框架下,将ilr、Dirichlet和FD方法应用于NHANES数据,分析24 h活动行为时间分布特征,用AIC和BIC准则评价3种方法拟合效果,比较3种方法在人群24 h活动行为时间成分数据的适用性。选择最优的拟合方法计算人群活动行为时间比例的均数和变异矩阵(ilr)或者标准差(Dirichlet和FD),描述人群24 h活动行为时间比例的集中趋势和离散趋势,并采用对数似然比检验(log likelihood ratio test,LLRT)比较活动行为时间分布的性别和年龄差异。
2.2 结果
2.2.1 研究人群24 h活动行为时间使用分布特征
采用ilr、Dirichlet和FD方法分析人群24 h活动行为时间分布特征(表2~表6)。
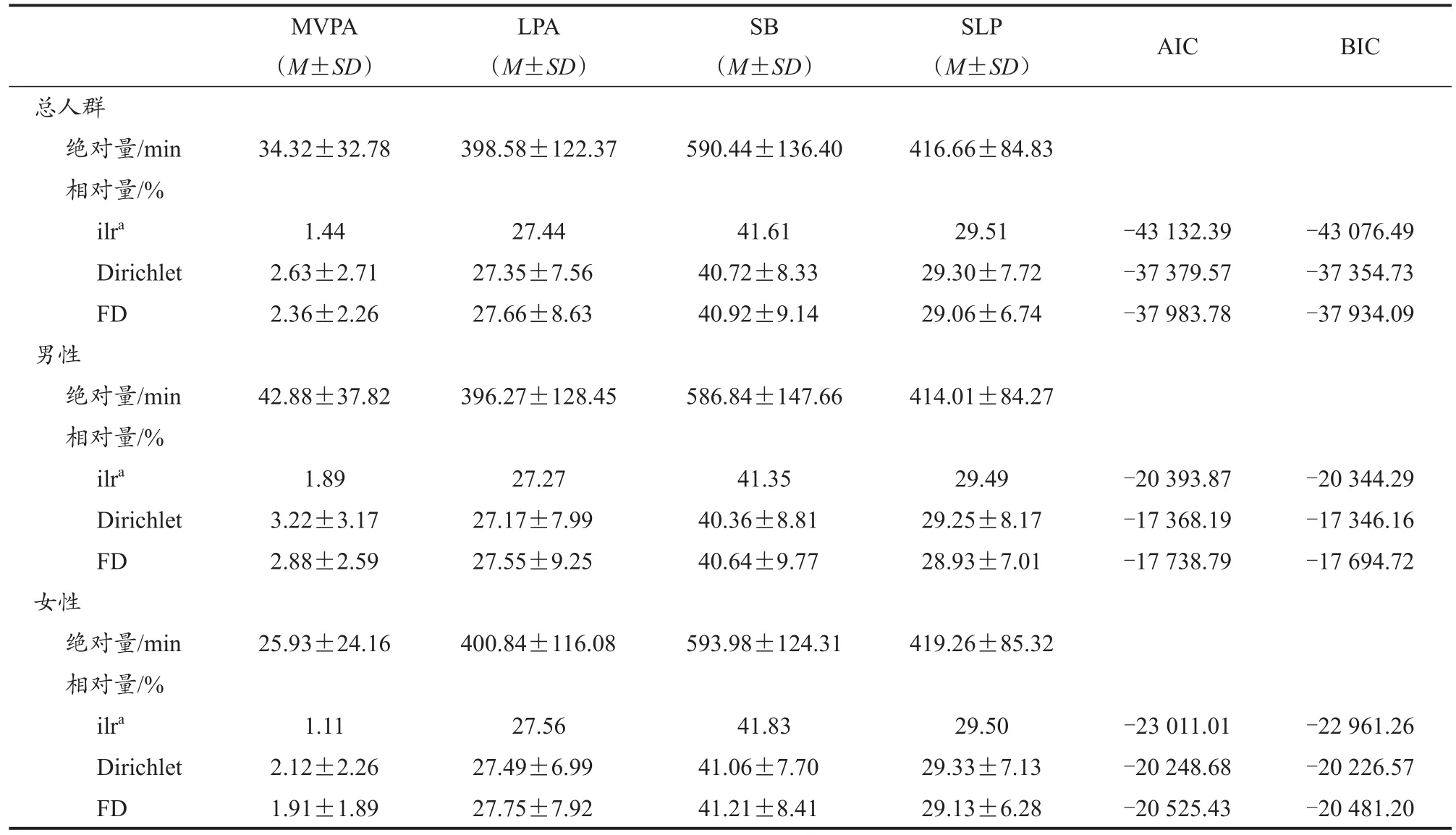
表2 不同性别研究人群24 h活动行为时间使用分布特征Table 2 Distribution Characteristics of 24 h Movement Time-Use in Different Gender Groups

表3 不同年龄研究人群24 h活动行为时间使用分布特征Table 3 Distribution Characteristics of 24 h Movement Time-Use in Different Age Groups
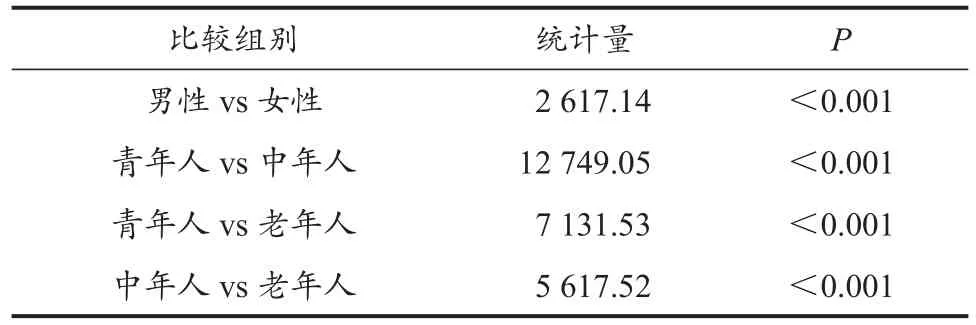
表4 不同性别、年龄研究人群24 h活动行为时间使用分布差异检验Table 4 Test of the Differences in the Distribution of 24 h Movement Time-Use among Different Gender and Age Groups
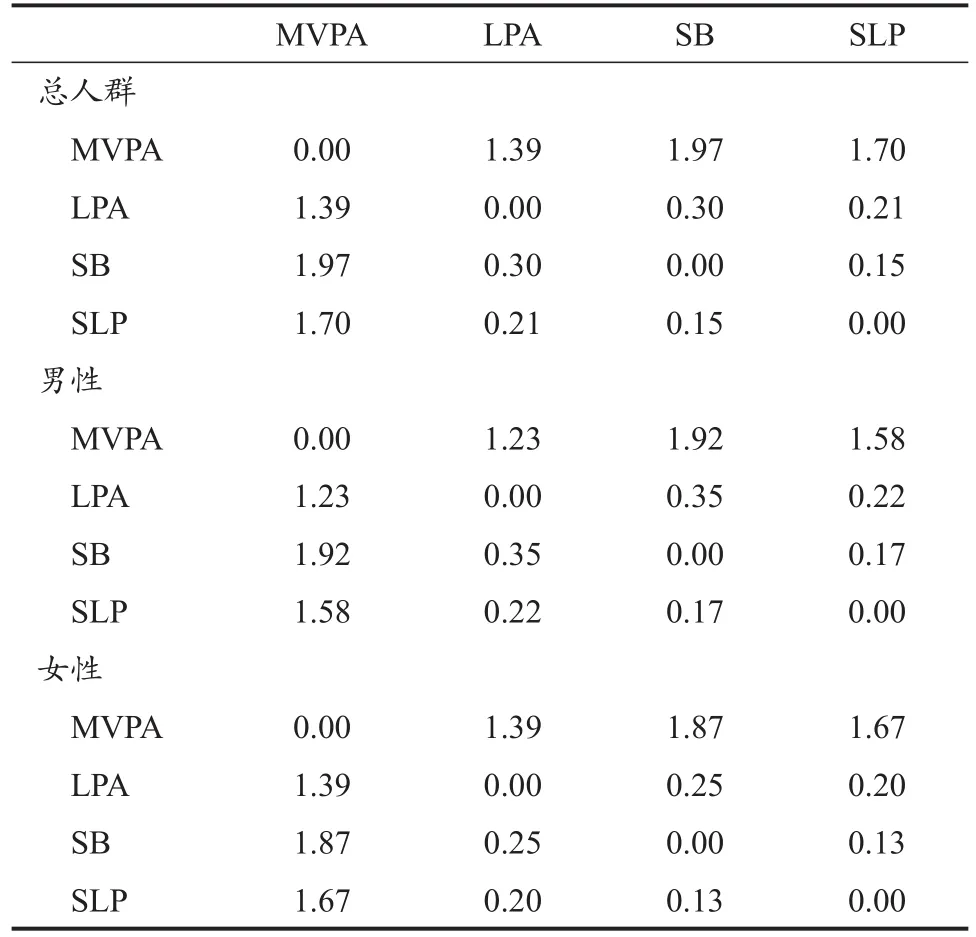
表5 不同性别研究人群24 h活动行为时间使用比例变异矩阵Table 5 Variation Matrix of Ratio for 24 h Movement Time-Use in Different Gender Groups
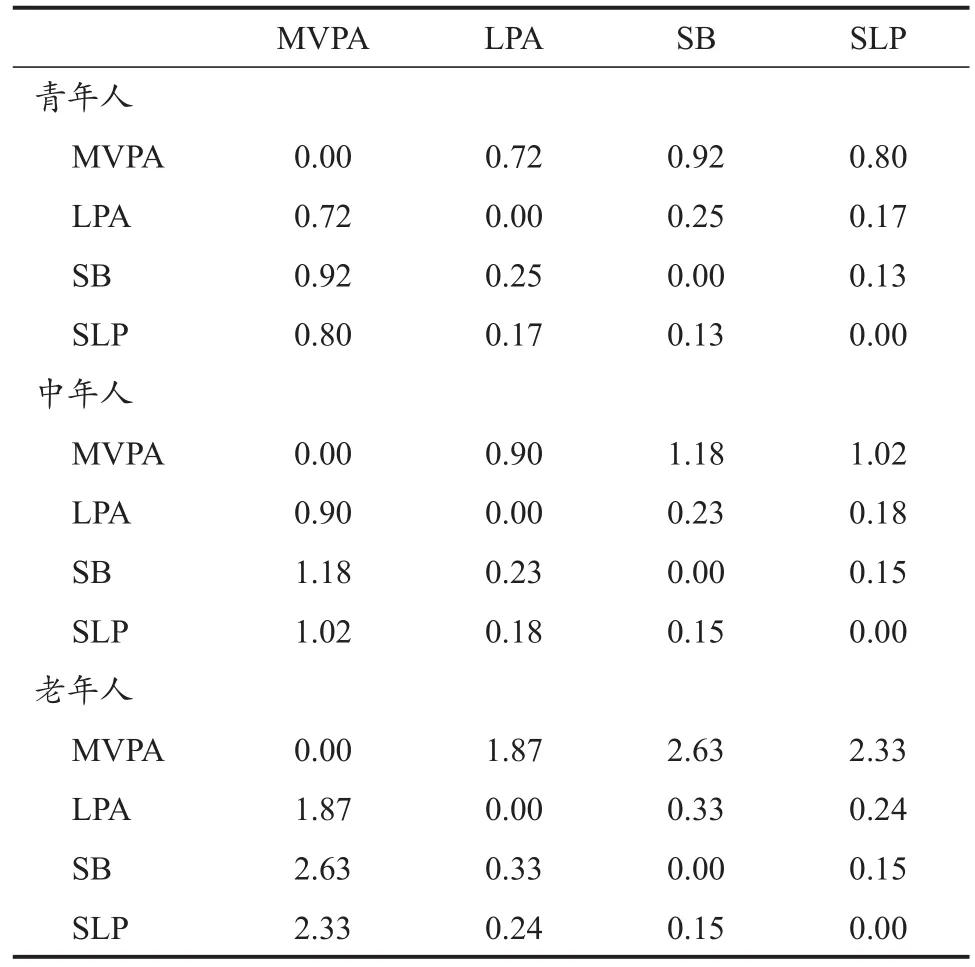
表6 不同年龄研究人群24 h活动行为时间使用比例变异矩阵Table 6 Variation Matrix of Ratio for 24 h Movement Time-Use in Different Age Groups
本研究发现(表2~表3),研究人群平均花费在MVPA、LPA、SB 和 SLP的时间分别为 34.32、398.58、590.44、416.66 min。无论是分性别还是分年龄的拟合优度结果均表明,ilr方法的AIC和BIC较小,更适合拟合研究人群24 h活动行为时间分布。总人群、男性、女性、青年人、中年人和老年人的ilr结果显示,一天中各人群用于SB时间的比例最大,其次为睡眠。
对数似然比检验结果显示,男性、女性24 h活动行为时间比例分布存在差异(表4),男性MVPA时间比女性高,SB时间比女性低(表2)。不同年龄段人群的24 h活动行为时间比例分布不同,相比于青年人,中年人和老年人MVPA时间比例更低,SB时间比例更高(表3)。
不同性别和不同年龄研究人群24 h活动行为变异矩阵结果显示,各人群MVPA时间比例均与其他行为时间依赖性较小,SB、SLP和LPA时间三者的依赖性较强(表5~表6)。
2.2.2 研究人群24 h活动行为时间使用分布特征可视化
采用三元图对ilr方法计算研究人群24 h活动行为时间比例分布结果进行可视化(图2)。
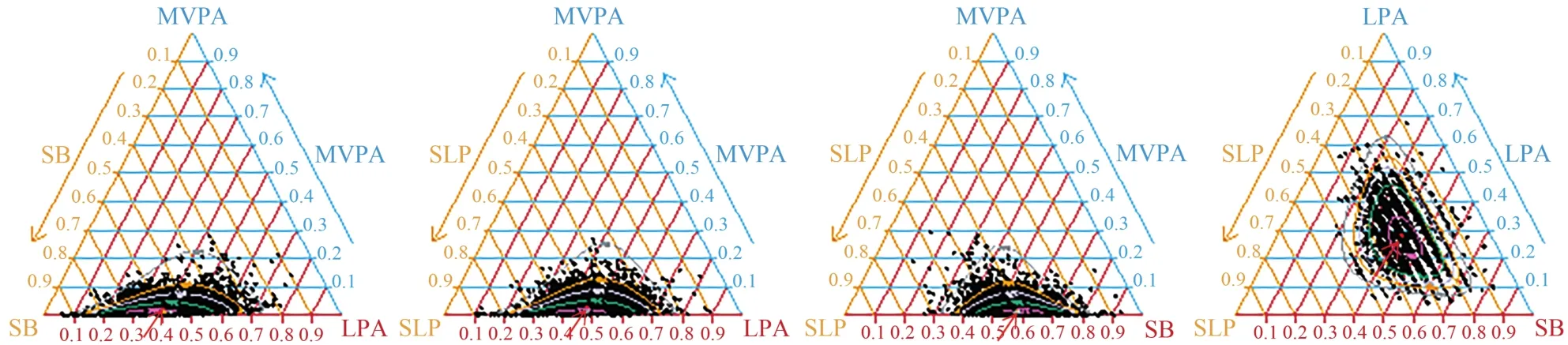
图2 ilr方法计算的总人群24 h活动行为时间使用比例三元图Figure 2.Ternary Diagram of Ratio for 24 h Movement Time-Use in the Total Population by ilr Method
研究显示,总人群MVPA时间比例方向的等密度曲线相对其他行为方向更疏散,即MVPA时间比例离散程度更大。
3 讨论
随着PA、SB和SLP健康效应研究的不断深入,证明除MVPA外,LPA和充足的睡眠也可以对人体健康产生益处(Chaput et al.,2016;Poitras et al.,2016),SB对多种健康指标都有不利的影响(Carson et al.,2016),且各行为间可以彼此缓和对健康的影响(Chaput et al.,2017)。仅考虑24 h活动行为连续谱中某个活动行为与健康的关系,限制了对活动行为间相互作用对健康影响的理解,24 h活动行为时间使用流行病学研究正成为当前公共卫生和运动科学等健康相关领域重点研究方向,但与此同时,将24 h行为时间使用数据视作成分数据,也给统计分析带来一定的挑战(Chaput et al.,2014;Dumuid et al.,2020),积极探索成分数据方法理论及应用对促进时间使用流行病学研究具有重要意义。
本研究介绍了ilr、Dirichlet和FD 3种成分数据方法及其优缺点。理论上,ilr方法消除了成分数据的定和限制,将成分数据从单形空间转换到欧式空间,避免成分数据建模时造成多重共线性问题,使得多元统计方法得以应用。ilr方法转换计算简便,成分均数以及变异矩阵可用于描述成分数据的集中趋势和离散趋势,但ilr方法在处理各种单形独立形式(如中立性)、重要的成分操作(如合并某些同质成分)存在一定困难。更重要的是,建模时ilr方法受标准正交基选取影响,分析结果不唯一,且模型参数解释原始成分变量不直观。此外,ilr方法采用变异矩阵描述成分内共同依赖性,变异矩阵元素取值越小,表明相应成分间共同依赖性越强,但无法明确相关方向。相比于ilr方法,Dirichlet和FD方法直接基于单形空间建模,结果更直观,采用建模后成分平均值±标准差描述成分数据的集中趋势和离散趋势。Dirichlet方法满足ilr方法不能满足的CoDA条件,即子成分一致性以及置换不变性等。由于Dirichlet成分隐含强独立结构、参数易解释,在很多情况下,Dirichlet被作为成分间具有强独立关系的成分数据建模标准参考,但Dirichlet的成分强独立结构、相关结构完全为负性质,不适于组分间弱正相关或强相关的成分数据建模。相比于Dirichlet方法,FD方法为Dirichlet方法的推广,在建模依赖性方面具有更大的灵活性,可通过配置不同参数适应各种独立形式的成分数据,满足成分数据更多的分析要求,更能捕获成分数据特征。但FD方法实际上是一种混合结构模型,具有强混合成分(集群)链接特点,通常的单模态参数化模型过于严格,导致未知的推理复杂度。FD方法因相关结构完全为负,不允许在成分之间建立正相关模型。因此,从理论上讲,3种方法在分析成分数据时各有优缺点,需结合成分数据实际情况选择合适的分析方法。实际应用中,成分数据方法拟合效果会受到样本量、成分比例、成分方差、成分相关性等因素的影响,模拟研究显示,在成分数据具有大样本、成分间比例相差越大、成分方差越小、正相关性越强情况下,ilr方法有更好的拟合效果(刘晴,2020)。而对于Dirichlet和FD模型适应的成分数据特征,需要后续更多的模拟研究进行探讨。
本研究将3种成分数据方法应用于NHANES人群的24 h活动行为时间的实例研究中,结果显示,该实例数据中ilr方法具有最好的拟合优度,即ilr方法能更准确描述人群的24 h活动行为时间分布特征。但鉴于目前鲜有研究采用Dirichlet或FD方法分析24 h活动行为特征和各类健康效应,3种成分数据方法适用条件仍在理论探索阶段,后续可根据ilr、Dirichlet和FD原理进行成分数据模拟研究,进一步探讨3种成分数据方法适用条件。ilr方法结果显示,16~85岁美国人群一天中MVPA时间为20.74 min,低于直接计算的绝对量34.32 min,也低于《美国身体活动指南》成年人平均每日MVPA最低推荐量32.14 min(Piercy et al.,2018)。16~85岁美国人群一天SB为599.18 min,略高于直接计算的绝对量590.44 min,但远高于2007—2016年基于问卷数据计算的NHANES人群的加权平均SB(342.00~474.00 min)(Du et al.,2019),目前尚未有成人SB具体推荐量,但《美国身体活动指南》建议多动少坐。现有研究表明,以《美国身体活动指南》的成人PA推荐量为参考,美国成人有氧和加强肌肉的PA达标率呈上升趋势,但变化不明显,总体达标率仍然较低(Du et al.,2019;Whitfield et al.,2019)。美国成人的SB时间较以前明显增加(Du et al.,2019)。另外,基于传统统计方法的研究表明,男性比女性更倾向于运动,在男性中,中年人更容易久坐;女性中,老年人更容易久坐(Azevedo et al.,2007)。但基于成分数据方法研究发现,男性比女性更不活跃,工作中年龄更小的成年人久坐时间更长(Gupta et al.,2018)。本研究发现,不同性别、年龄的人群24 h活动行为时间使用分布存在一定差别,且男性的MVPA时间比女性长,SB时间比女性短。相比于青、中年人,老年人的MVPA时间更短,SB时间更长。研究结果不一致的原因可能与统计分析方法、数据收集方式及时间等因素有关,但研究均表明年龄和性别是PA、SB的两个潜在重要决定因素。本研究采用的是2005—2006年NHANES数据,时效性较差,但该年的身体活动数据是基于加速度计收集的。在人体活动测量中,加速度计较于问卷更具客观、精确、实用(向剑锋 等,2015;赵壮壮 等,2015;Dyrstad et al.,2014),将其获得数据用于方法学实例研究结果更可靠。
4 结论
ilr、Dirichlet和FD方法理论上各有优缺点,需结合成分数据实际情况选择合适的成分数据方法分析。本研究将3种方法应用于2005—2006年美国NHANES人群中分析24 h活动行为时间比例数据,发现ilr有最好的拟合优度。未来的研究仍需更多模拟和应用研究,探索各种成分数据方法适应的数据特征,以促进时间使用流行病学研究,对制定人体24 h活动指南、提升人体体质健康水平有着重要意义。
