综放工作面过空巷矿压显现规律及控制技术研究

卢 恒，张传宝，仵振华，王禹昌

(国家能源集团 神华神东煤炭集团大柳塔煤矿连掘二队，陕西 榆林 719000)

由于历史原因，很多中小型煤炭企业，尤其是以前存在的小煤窑一味追求煤炭产量，对煤炭无序开采导致资源大量浪费，更严重的是，造成我国众多煤矿工作面开采将面临过空巷的危险[1-3]。空巷影响工作面前方顶板稳定性，易导致顶板大面积垮落、压架事故，给矿井的安全生产带来严峻的挑战[4-9]。

目前国内众多学者对工作面过空巷期间顶板覆岩特征、矿压显现规律进行了大量的研究，徐青云[10]等通过建立空巷基本顶力学模型，揭示了空巷顶板稳定机理，确定顶板破断产生滑落失稳是造成压架的主要原因；刘畅[11]等通过相似模拟得到了工作面过大断面空巷基本顶会超前破断，基本顶上方亚关键层随基本顶破断、滑落；尹超宇[12]等运用尖点突变理论研究工作面与空巷之间煤柱的失稳机理，认为煤柱宽度等于临界危险宽度时，煤柱的塑性破裂区面积与煤柱总面积间满足定量关系而发生能量控制型突变失稳；郭富利[13]以综放工作面空巷作为研究对象，以Winkler地基梁理论为基础建立对应上覆岩体关键结构力学模型，对关键结构的稳定性进行研究，认为关键块断裂位置与直接顶性质有关，并计算判定断裂位置位于空巷上方；谢生荣[14]等基于工作面过空巷基本顶破断的结构模型，得到过空巷时长关键块条件下的支架临界工作阻力，采用数值模拟方法分析综放工作面过空巷时采动影响下围岩应力分布、变形与破坏特征。根据关键层理论[15]可知，采场矿压与覆岩关键层结构破断特征及其运动规律密切相关，悬臂梁结构对支架压力影响显著大于砌体梁结构，而砌体梁结构时，支架上方断裂关键块体形态显著影响支架压力[16]，因此空巷通过影响基本顶断裂特征间接影响了支架压力载荷。

工作面空巷支护多采用木垛、锚杆(索)支护等形式，但其控制效果不佳，而高水材料充填技术能有效地解决工作面过空巷的难题，该技术主要研究充填材料配比、充填体强度、充填体与围岩相互作用关系、充填对顶板影响等[17-21]。

笔者在前人研究的基础上，对于综放工作面过空巷矿压显现规律进行研究，分析工作面推进过程中前方煤柱失稳破坏特征、顶板偏应力演化规律，以及空巷对顶板断裂的影响规律；采用数值模拟计算的方法研究工作面过空巷围岩控制技术，确定合理控制方案，为同类型综放工作面采用过空巷技术提供重要的借鉴意义。

1 工程概况

某矿3-802工作面位于该矿八采区，底板标高+490～+570 m，地面标高+921～+945 m，采用放顶开采工艺，采放比1∶1.4，工作面走向长度1 170 m，倾向长度213 m；主采3号煤层，煤层平均厚度6.2 m，该煤层稳定，平均倾角5°。工作面的顶底板岩性如图1(a)所示。

在距离工作面357 m和961 m处发育X8-6、X8-9陷落柱，该陷落柱充填密实，导水性差，不影响工作面的正常开采。工作面最大涌水量预计220 m3/h；瓦斯绝对涌出量11.04 m3/min，不易自燃，煤尘具有爆炸性。

现场调研显示，工作面开采至450 m处时，工作面前方将揭露遗留空巷，该空巷为矩形巷道，沿煤层底板掘进，断面规格3 m×2.8 m，长度为161 m，原支护为锚杆(索)支护。在工作面推进过程中，空巷贯通前、后必然对工作面安全生产造成影响，给现场安全管理带来巨大困难。工作面及空巷的位置关系如图1(b)所示。

图1 顶底板岩性及工作面空巷位置关系Fig.1 Relationship between lithology of roof and floor and position of goaf in working face

2 工作面过空巷煤柱应力、塑性区演化规律

2.1 工作面超前支承应力分布

工作面与空巷之间煤柱的载荷与工作面前方超前支承应力的分布有关，研究工作面前方超前支承应力的分布有助于剖析煤柱破坏规律。

运用极限平衡理论[22-23]建立工作面超前支承应力的计算模型，如图2所示。图中Px为煤壁支护阻力，MPa；x为距煤壁的距离，m；K为超前支承压力集中系数；γ为岩层容重，kN/m3；H为岩层埋深，m。0～x0部分为塑性区，x0～x1为弹性区。

图2 超前支承应力计算模型Fig.2 Calculation model of front abutment support pressure

从图2中塑性区内取一单元体，由x方向的受力平衡可知

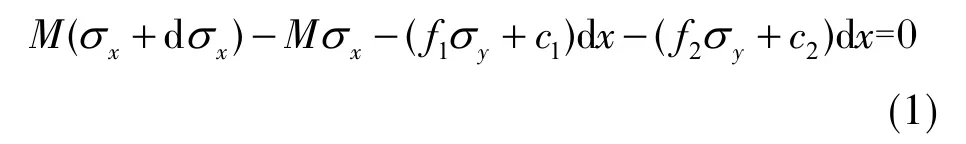
式中，σx为煤体水平方向应力，MPa；f1，f2为层面摩擦因数；c1为煤体与直接顶或伪顶岩层间的黏聚力，MPa；c2为煤体与直接底岩层间的黏聚力，MPa；M为煤层开采高度，m。

假定塑性区内煤体屈服满足莫尔-库仑准则，即满足

式中，Sc=2ccosφ/(1-sinφ)，ε=(1+sinφ)/(1-sinφ)；φ为煤体的内摩擦角，(°)。

将式(2)代入式(1)得到

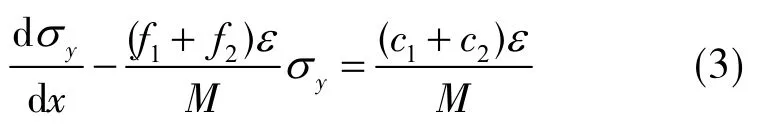
考虑边界条件，当x=0时，σx=Px，求得

将x=x0的边界条件σy=KγH代入式(4)，计算得到超前支承应力峰值点的位置为

从图2弹性区内取一单元体，由x方向的受力平衡可知

弹性区内满足：σx=λσy，dσx=λdσy，其中λ=μ/(1-μ)，μ为泊松比；代入式(6)，同理考虑边界条件，求解得到

将x=x1的边界条件σy=γH代入式(7)中，得到超前支承应力作用的最远处位置为

2.2 数值模型的建立

根据3-802工作面的围岩地质条件建立FLAC3D数值计算模型，如图3所示。数值模拟中的煤层、顶底板力学参数见表1。模型长度x方向(工作面推进方向)为300 m，宽度(y方向)为200 m，垂直方向(z方向)为55 m。模型的顶部施加均布载荷q=9.8 MPa，用以模拟原岩应力，四周及底边固定位移，设定法向约束。工作面埋深取430 m，侧压系数取1.2，开挖区域保持与模型边界相距50 m，以减少边界效应的影响。空巷的开挖宽度取实际宽度3 m，为了重点研究煤柱宽度对采场矿压的影响，简化模型使空巷与工作面推进方向垂直布置，各岩层均使用莫尔-库仑材料模型，并采用文献[24]中的双屈服模型来模拟采空区矸石压实作用。由于空巷原有锚杆(索)支护强度较低，因此模拟过程中未考虑支护的影响。模型模拟过程：原岩应力平衡→开掘空巷道→开挖工作面→充填采空区。

图3 数值模拟模型Fig.3 Numerical simulation model

表1 数值计算模型中的煤岩体力学参数Table 1 Mechanical parameters of coal and rock mass in numerical calculation model

2.3 煤柱应力及塑性破坏规律

根据工作面的围岩地质条件，通过理论计算及数值模拟得到了工作面前方超前支承应力曲线，如图4所示。理论计算中的各参数根据现场实际情况得到：M=6 m；φ=20°；μ=0.25；假设各层面摩擦因数相等，煤层与直接顶和直接底界面的黏聚力相等，即f1=f2= 0.2，c1=c2= 1.5 MPa；应力集中系数K为2～3，根据现场测试结果，取3；煤壁支护阻力Px为0.3 MPa；γH=10.75 MPa。

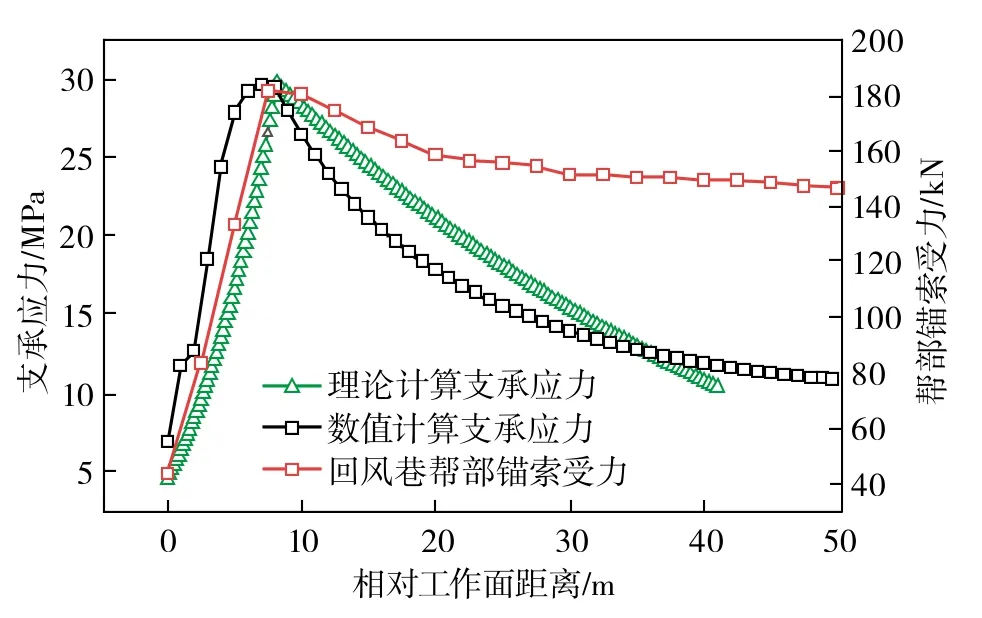
图4 超前支承应力分布及锚索受力曲线Fig.4 Front abutment support pressure distribution and stress curves of anchor cable

由图4可知，理论计算与数值模拟计算得到的超前应力分布较为吻合，峰值点及峰值应力相差较小，超前应力分布影响范围相差7 m，但主要高应力影响范围基本一致；该工作面回采巷道帮部锚索受力曲线显示当工作面距离测点8 m左右时锚索受力值最大，当距离工作面约50 m后，锚索受力趋于稳定，验证了超前应力分布的合理性；综合显示该工作面超前影响范围在45 m左右。

根据超前应力的影响范围可知：当工作面推进到距离空巷50 m时，工作面超前应力与巷道两侧应力开始产生叠加作用，煤柱开始在高应力作用下发生失稳破坏，笔者通过数值模拟的方法来研究工作面推进到离空巷50，45，40，35，30，25，20，15，10，5 m时的煤柱应力分布及塑性破坏规律；模拟过程中工作面的宽度和长度保持不变，应力值取煤柱垂直方向中间位置。

图5为不同煤柱宽度下工作面前方垂直应力分布曲线，空巷的位置为图中坐标0～3 m处。由图5可知，当工作面前方与空巷煤柱宽度为15～50 m时，煤柱侧垂直应力峰值随着煤柱的宽度减小而不断增大；当煤柱宽度为5～15 m时，煤柱垂直应力峰值随着煤柱的宽度减小而不断减小；实体煤侧垂直应力峰值随着煤柱宽度的减小而不断增大。在不同煤柱宽度下，实体煤侧垂直应力曲线均为“单峰”型，而在煤柱侧，在煤柱宽度为20～50 m时，垂直应力曲线均为“双峰”型，并且随着煤柱宽度的减小，煤柱垂直应力双侧峰值应力均不断增大；在煤柱宽度为5～20 m时，垂直应力曲线均为“单峰”型，在煤柱宽度为20 m时煤柱的垂直应力达到最大值32 MPa；煤柱宽度为5 m时实体煤侧垂直应力达到最大值28 MPa。综上说明工作面前方离空巷越近，煤柱越窄，煤柱垂直应力越高，失稳破坏的趋势越大。

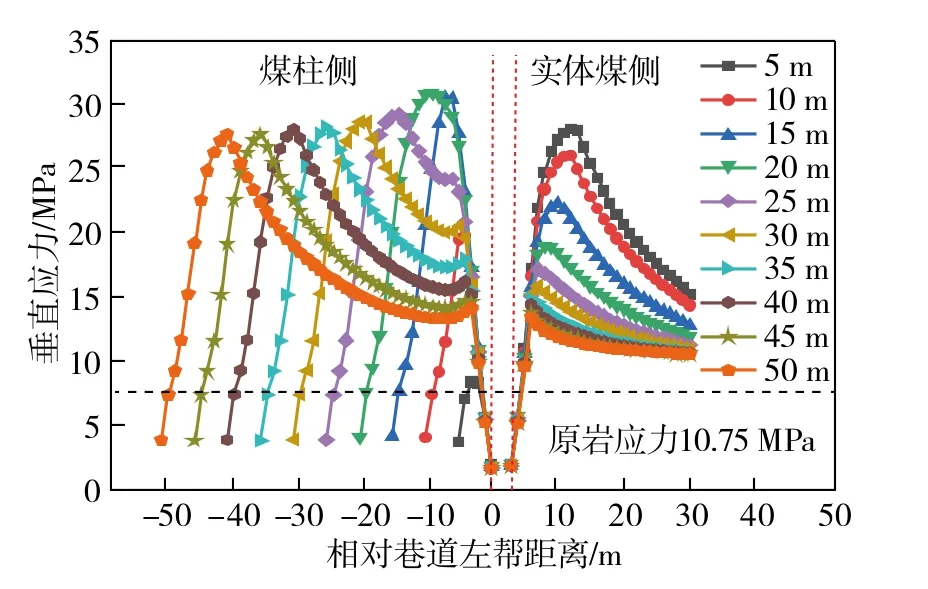
图5 不同煤柱宽度下工作面前方垂直应力分布Fig.5 Vertical stress distribution in front of working face under different coal pillar widths

图6为不同煤柱宽度下工作面前方煤体塑性区分布，从图6可知，当煤柱宽度为20～50 m时，在煤柱的中部并没有塑性破坏，而靠近工作面侧及空巷侧煤柱塑性破坏范围随着煤柱宽度的减小而增大；当煤柱宽度小于20 m时，煤柱完全失稳破坏，随着煤柱宽度减小，空巷右侧实体煤区域塑性破坏范围不断增大。

图6 不同煤柱宽度下工作面前方煤体塑性区分布Fig.6 Distribution of coal plastic zone in front of working face under different coal pillar widths

综上，在工作面不断推进的过程中，随着煤柱宽度的不断减小，超前应力与空巷两侧应力叠加作用不断增强，煤柱塑性破坏程度随着叠加应力的增大而增大；当煤柱宽度小于20 m时，煤柱在高应力下破坏严重，空巷围岩处在大变形中，工作面前方煤体的稳定性极差，对工作面前方顶板的变形将带来潜在危害。

3 工作面过空巷顶板破断规律

3.1 基本顶破断前力学模型建立

工作面过空巷过程中，由于工作面前方煤体失稳破坏，导致工作面顶板悬露面积和支架控顶长度大幅增大，致使顶板断裂位置发生改变，巷道上方顶板断裂线的位置影响着空巷的稳定性，进而影响工作面前方的安全生产。因此笔者结合Winkler弹性基础梁模型[25]对基本顶断裂位置进行研究，取工作面中部位置顶板按砌体梁理论进行分析，由于空巷离工作面起始位置较远，仅考虑顶板周期破断。

图7(a)～(b)分别为工作面前方有无空巷时基本顶破断前力学模型。图中q0为上覆岩层载荷，q1为采动引起的侧向载荷增量部分；M0，Q0和N分别为工作面前方煤壁位置(x=0)所对应的梁截面弯矩、垂直和水平方向的内力；已断裂岩块对其作用力为N′和Q′；qc为悬伸部分的分布载荷，包括基本顶自重及上部软岩岩层所受重力；b为超前支承应力影响范围，根据前文计算取50 m；L为悬臂梁悬伸的长度；xb为空巷宽度；xa为煤柱宽度。

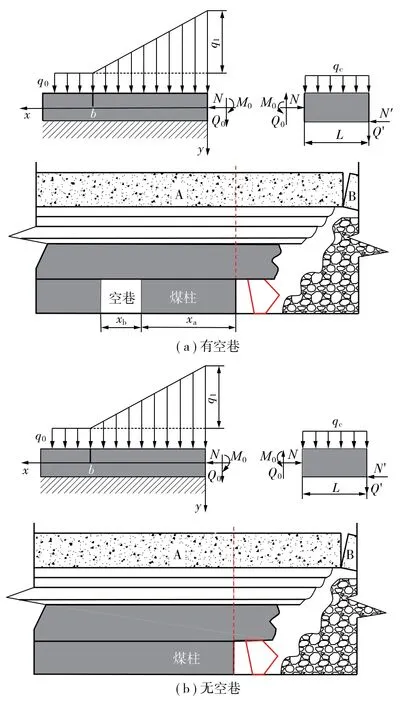
图7 基本顶破断前力学模型Fig.7 Mechanical model before main roof fracture

3.2 基本顶破断前力学模型求解

3.2.1 有空巷时

质量监管组的总满意率96%，常规调剂组的总满意率72%，组间总满意率对比，差异有统计学意义（P＜0.05）。见表1。

在采动影响范围内的采动载荷可以表示为

式中，q0=γH；q1=K′γH，K′为应力增加系数，根据前文取2。

假设把直接顶、煤层、直接底岩层看成基本顶岩梁下的Winkler地基基础，垂直位移与压力集度呈正比，即

式中，p为基本顶岩层上的覆岩压力增量，Pa；y为基本顶的垂直位移，m；k为地基系数，与基本顶下部直接顶、煤层和底板的厚度和力学性质有关，其值的大小为煤岩的弹性模量与煤层开采高度之比，经计算取0.06。

根据Timoshenko解[11]，可得有空巷时煤柱及实体煤上方基本顶梁弯曲变形微分方程为

式中，E为基本顶弹性模量，GPa，在平面应变条件下，E应取值E/(1 -u2)，u为泊松比；I为单位宽度基本顶的惯性矩，I=b1h13/ 12，b1为基本顶宽度，平面模型中取1；h1为基本顶厚度，取8.5 m。

将式(10)代入式(11)，并令

式(13)为四阶常系数非齐次微分方程，它的解由其对应的四阶常系数齐次微分方程通解Y(x)和特解Y＊(x)组成。

通解Y(x)根据特征值法可表示为

其中

式(13)的特解为

因此得到式(13)的通解为

考虑x=0时的边界条件，则

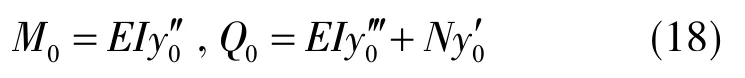
根据式(17)，(18)[26]求得

将式(19)代入式(17)便可求出煤柱及实体煤上方基本顶岩梁的竖向位移方程为

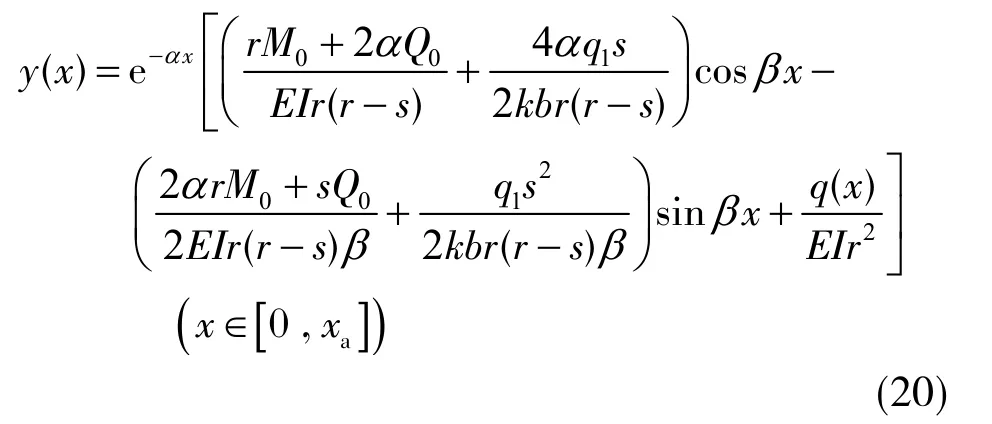
由式(20)求得基本顶的弯矩方程为

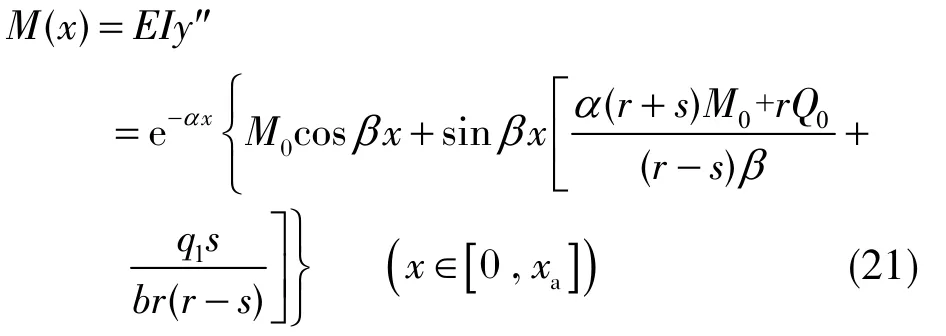
空巷存在时，空巷位置处基本顶下侧各岩层不连续，因此空巷上方基本顶梁弯曲变形微分方程不考虑基本顶岩层上的覆岩压力增量p，得到

将式(12)代入式(22)得到

同理得到：式(23)的通解由其对应的四阶常系数齐次微分方程通解Y1(x)和它的特解Y1＊(x)组成。

由于s＞0，四阶常系数齐次微分方程通解可以表示为

式中，C1，C2，C3，C4为常数。

式(23)的特解为

由此得到方程(23)的通解为

由此求得空巷上方基本顶的弯矩方程为

在x0处的边界条件为

实体煤上方与基本顶梁弯曲变形微分方程一致，同理求得实体煤上方基本顶竖向位移及弯矩方程为

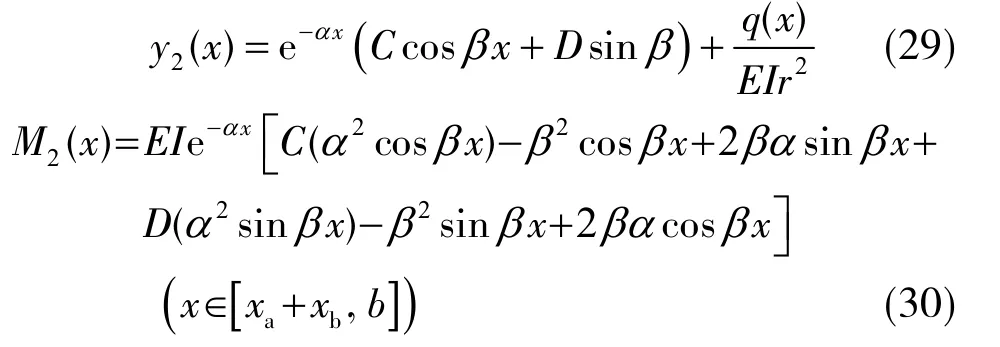
在xa+xb处的边界条件为

3.2.2 无空巷时

当没有空巷影响时，基本顶弯矩方程与式(21)一致，x的取值范围为：0＜x＜b。根据工作面的实际情况及计算得到，E=24 GPa，I=53.005 m4，k=0.06，M0=3 198.375 MN·m，γ=25 kN/m3，r=0.006 m-2，N0=168.75 MN，Q0=168.45 MN，s=0.000 132 7 m-2，b=45 m，q0=10.75 MPa，q1=20 MPa，xa取5 m，xb分别取3，4，5 m。

利用工程计算软件Mathcad对有无空巷基本顶弯矩进行计算，结果如图8所示。

图8 基本顶断裂前弯矩Fig.8 Bending moment before main roof fracture

由图8可知，当工作面前方存在空巷时，基本顶弯矩峰值显著增大，峰值点向工作面前方移动，其中无空巷时，峰值点距离工作面8 m，峰值弯矩3 962 MN·m；空巷宽度2 m时，峰值点距离工作面16.6 m，峰值弯矩6 627 MN·m；当空巷宽度3 m时，峰值点距离工作面18.2 m，峰值弯矩6 830 MN·m；当空巷宽度4 m时，峰值点距离工作面19.6 m，峰值弯矩6 927 MN·m。当基本顶弯矩超过其极限弯矩时，基本顶将在弯矩峰值处发生断裂。因此得到结论：由于空巷的影响，基本顶断裂位置将向工作面前方移动；基本顶断裂线前移，将导致空巷处在关键块体B的下方，受其强烈回转变形影响，空巷将剧烈变形，导致工作面液压支架工作阻力急剧增大，诱发压架事故。

4 工作面推进过程中顶板偏应力不变量演化规律

为了更深入了解工作面推进过程中，空巷对工作面基本顶变形失稳的影响，对工作面推进过程中顶板偏应力不变量演化规律进行研究。由于偏应力第二不变量J2能全面反映岩体的畸变能及剪应力大小[27-29]，由此笔者选取J2为评价顶板稳定性的指标。J2的表达式可简化为

式中，σ1，σ2，σ3分别为第一、第二、第三主应力。

而畸变能与J2的关系为

式中，G为剪切模量或刚性模量，GPa。

本文通过数值模拟的手段，获取煤柱宽度分别为5，10，15，20 m时基本顶J2的相关参数，通过Origin软件进行数据处理得到工作面推进到不同位置时基本顶J2分布图及工作面中部基本顶J2分布曲线，分别如图9～10所示。

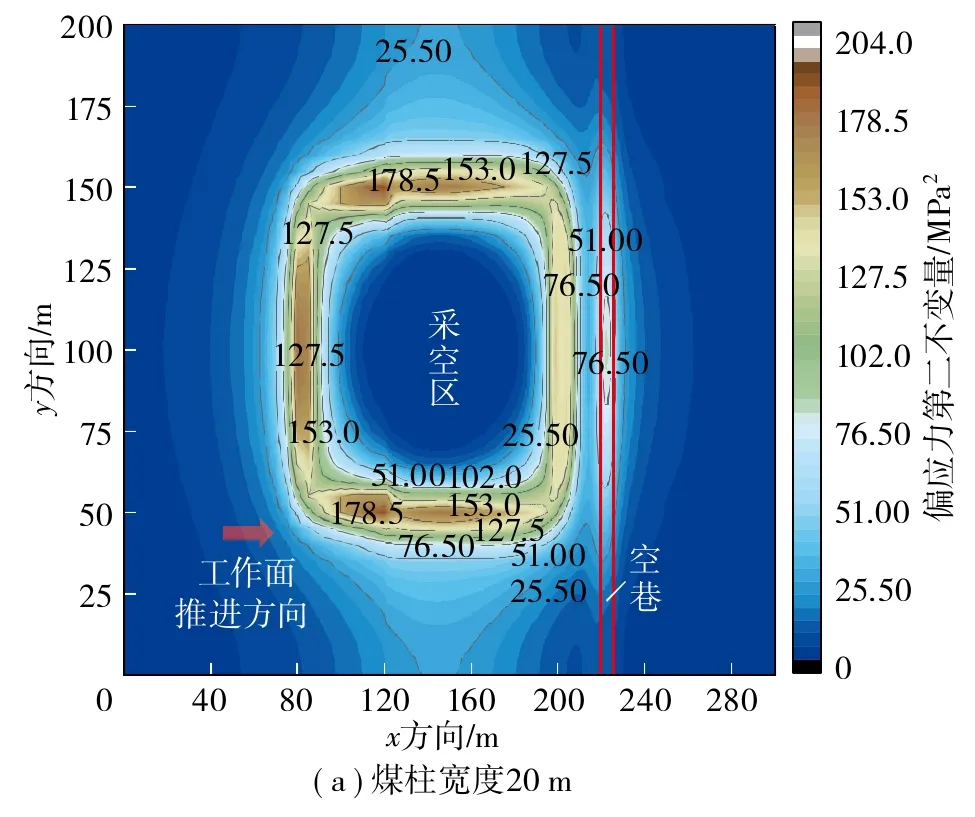
图9 不同煤柱宽度下基本顶J2分布Fig.9 Distribution of main roof J2 under different coal pillar widths

由图9～10可知，工作面开挖后，类似于支承应力向采空区周围深部围岩转移，形成应力集中区，基本顶偏应力分布也具有同等规律，采空区上方基本顶J2值较低，接近于0；而在四周基本顶J2值较高，形成高偏应力集中区；倾斜方向工作面两侧实体煤上方顶板J2值呈对称分布；在工作面推进方向，两端顶板J2值呈不对称分布。综上，说明工作面开挖后，采空区上方顶板垮落后，岩层运动趋于稳定，顶板畸变能较小；而在采空区四周由于应力集中，导致该区域顶板畸变能较大，当畸变能超过极限时，顶板趋于断裂。

图10 不同煤柱宽度下基本顶中部J2分布曲线Fig.10 Distribution curves of J2 in the middle of main roof under different coal pillar widths

当工作面相对空巷距离不同时，工作面前方顶板J2分布规律不同，当煤柱宽度大于10 m时，工作面前方顶板J2呈现双峰值分布，第1个峰值靠近煤壁上方顶板，而第2个峰值位于空巷上方，明显看出第1个J2峰值随着煤柱宽度的减小而降低，第2个J2峰值随着煤柱宽度的减小而增大；煤柱宽度20 m时，第1个J2峰值高于第2个J2峰值，随着煤柱宽度的减小，第2个J2峰值逐渐高于第1个J2峰值；对比无空巷影响的一端，存在空巷时，上方顶板J2峰值低于无空巷时，但顶板高J2值区域更大，且当煤柱宽度小于5 m时，顶板J2峰值接近于无空巷侧。这说明，当工作面前方存在空巷时，顶板偏应力转移到空巷上方顶板，导致该区域顶板畸变能增大，并随着煤柱宽度的减小而进一步增大，当畸变能达到岩体极限时，顶板将发生破断，能量释放，导致顶板的破断位置向前方移动，与上文基本顶弯矩的计算结果相符。

5 工作面过空巷围岩控制技术

5.1 工作面过空巷围岩控制数值模拟

根据前文研究显示：当空巷未采取合理措施时，工作面过空巷过程中，煤柱失稳变形，顶板悬露面积增大，顶板断裂位置超前移动，导致空巷及支架上方基本顶断裂岩块长度增大，岩块回转应力增大，支架及空巷围岩应力增大，容易引发压架事故。

因此需采取合理的空巷加强支护方案来加固围岩，阻止基本顶超前破断。而传统的锚杆(索)支护无法对空巷上方顶板的大结构变形产生影响，而目前在工作面过空巷时，广泛地使用木垛或高水材料充填支护空巷，维护工作面前方的稳定。笔者通过数值模拟分别研究工作面过空巷时，对空巷进行木垛支护、高水材料充填支护时空巷及顶板控制的效果，并确定合理控制方案。数值模拟支护方案为：① 单木垛支护；② 双木垛支护，间距1 m；③ 双木垛支护，间距2 m；④ 不同充填体强度下的高水材料充填支护。方案中木垛长度均为3 m，直径0.16 m，支护强度0.5 MPa。木垛及充填体均采用莫尔-库仑材料模型，模型中充填材料参数见表2。

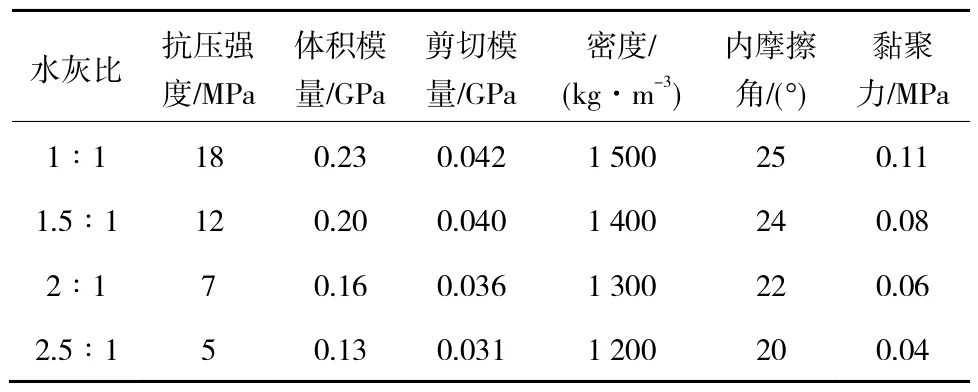
表2 充填材料参数Table 2 Filling material parameters

图11为木垛支护下基本顶J2分布。由图11可知，当工作面推进到距离空巷间距5 m时，无控制和单木垛、双木垛(间距2 m)情况下基本顶的偏应力都呈单峰值分布，三者峰值点的位置基本在一个区间，J2值差异不大；当对空巷进行双木垛(间距1 m)支护时，偏应力分布趋势相同，但J2峰值明显增大，其峰值点距工作面的距离缩短，约减小6 m，距工作面前方0～35 m基本顶J2值均大于无控制条件。

图11 木垛支护下基本顶J2分布Fig.11 Distribution of main roof J2 under timber crib support

图12为充填支护下基本顶J2分布。

图12 充填支护下基本顶J2分布Fig.12 Distribution of main roof J2 under filling support

由图12可知，当对空巷进行充填支护时，不同水灰比条件下，相对于无控制的情况顶板偏应力分布都发生了明显的变化，J2峰值均明显增大，J2峰值点向工作面位置靠近，其中当充填材料水灰比为1∶1时，充填体的强度最大，导致顶板J2峰值最大，增大的幅度最大，峰值点距离工作面距离最近；充填条件下工作面前方0～10 m基本顶的偏应力显著大于无控制条件。

综上，说明对空巷进行支护后，基本顶偏应力主要集中在工作面前方0～10 m位置，反映了该区域内基本顶岩体内畸变能及剪应力较大，该区域的顶板更易于破坏，偏应力峰值向工作面前方移动也进一步说明了顶板断裂位置向工作面移近了，减小了顶板超前断裂的概率，能够避免压架事故的发生。

为了进一步分析各控制方案的效果，通过数值模拟得到了不同控制方案下空巷围岩塑性区的分布范围，如图13所示。由图13可知，木垛支护下空巷围岩塑性破坏程度变化不明显，塑性破坏范围减小量较小；相对于无支护及木垛支护，充填支护下，巷道围岩塑性破坏程度明显减小，尤其是巷道上方直接顶板的塑性破坏范围明显减小，充填材料的水灰比越小，充填体强度越大，围岩塑性破坏程度越小。

图13 不同控制措施下空巷围岩塑性区分布Fig.13 Distribution of plastic zone of surrounding rock of goaf under different control measures

5.2 现场工业性实践

综合考虑工作面过空巷围岩控制数值模拟研究的结果、现场情况、经济效益等方面，决定对所研究工作面过空巷时，对空巷采取分区控制的策略。

对空巷靠近运输巷的80 m段采用木垛支护，具体参数为：圆木直径0.16 m，长度3 m，配合1 000 mm×300 mm×100 mm的木质垫板垂直于空巷顶底板由外向里进行支设，每排支设2根，排距3 m，木点柱间距1 m，距离两帮分别为1 m；靠近工作面中部80 m段的空巷区域受超前应力影响更大，应力集中程度更高，对该区域采用高水材料充填支护，水灰比2∶1，充填高度2.5 m。

现场对空巷进行加强支护后，工作面安全地通过了空巷；在工作面过空巷的过程中，对空巷不同分区支架工作阻力进行现场实时监测，每个分区选3个支架进行数据收集处理，选取支架布置测站并进行编号(1～6号)，支护及监测示意如图14所示，监测的结果如图15所示。

图14 分区支护及支架测站布置示意Fig.14 Layout of divisional support and support stations

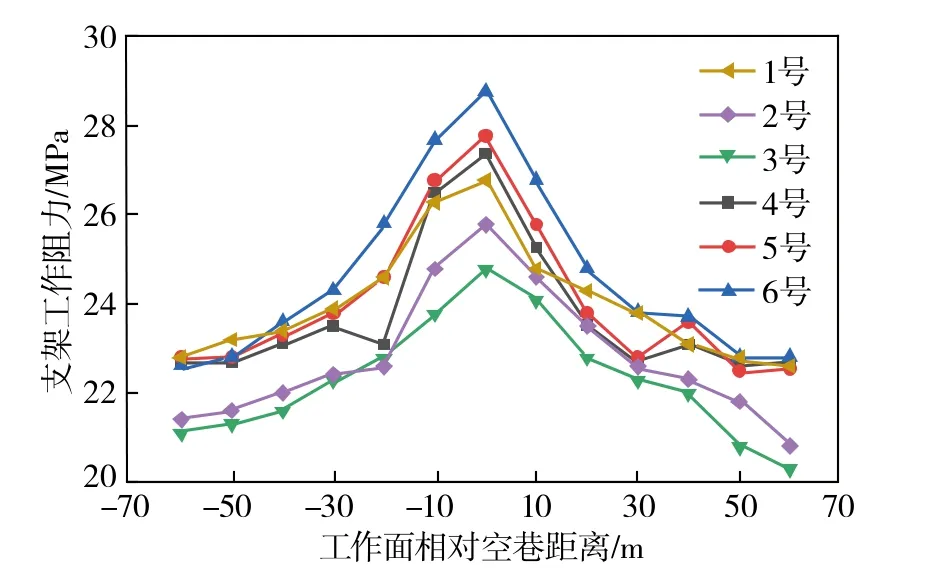
图15 不同位置的支架工作阻力监测曲线Fig.15 Monitoring curves of support working resistance at different positions

图中1～3号为过空巷时木垛支护区的液压支架工作阻力曲线，4～6号为过空巷时充填支护区的液压支架工作阻力曲线。整体来看，空巷支护后，工作面过空巷时，液压支架工作阻力都有一定程度的增大，工作面充填支护区域过空巷时的支架工作阻力总体大于过木垛支护区域。1号支架由于受超前应力与巷道两侧应力的叠加影响，导致液压支架工作阻力较大。液压支架工作阻力增量最大的是靠近工作面中部的6号支架，其工作阻力由22.8 MPa增至29.0 MPa，增加27.19%，其最大压力低于支架安全阀的开启压。以上说明了该控制方案可保证工作面能顺利通过空巷。

6 结 论

(1)通过极限平衡理论计算、FLAC3D数值计算对工作面开采超前支承应力分布进行研究，结果显示超前支承应力影响范围约45 m，应力峰值约30 MPa；利用数值模拟的手段对工作面推进过程中，空巷两侧支承应力及煤柱、实体煤塑性破坏范围进行研究，结果表明工作面推进过程中，当煤柱宽度为20～50 m时，煤柱垂直应力曲线均为“双峰”型，并且随着煤柱宽度的减小，煤柱垂直应力双侧峰值应力均不断增大；当煤柱宽度为5～20 m时，煤柱垂直应力曲线均为“单峰”型，且垂直应力峰值随煤柱宽度而减小；其中煤柱宽度为20 m时煤柱的垂直应力达到最大值。煤柱塑性破坏程度随煤柱宽度减小而增大，当煤柱宽度小于20 m时，空巷围岩破坏塑性严重，煤柱完全失稳破坏。

(2)基于Winkler弹性基础梁理论建立基本顶破断力学模型，分别对工作面前方有无空巷影响下的基本顶弯曲分布方程进行求解，得到了空巷宽度分别为2，3，4 m的基本顶弯矩分布曲线，结果显示空巷将导致顶板弯矩增大，峰值点向工作面前方移动，可能诱发顶板超前断裂，使支架阻力突增，导致压架事故；且空巷宽度越大，基本顶弯矩越大，峰值点离工作面越远。

(3)通过偏应力理论，对工作面推进过程中工作面前方基本顶偏应力不变量演化规律进行研究，以J2为评价指标，结果显示：由于空巷的影响，导致工作面前方基本顶J2呈双峰值分布，第1个峰值点位于煤壁上方附近，第2个峰值位置位于空巷上方，且距离空巷越近，J2峰值越大，两峰值点不断移近。验证了空巷将诱发顶板超前断裂，导致压架事故产生的结论。

(4)采用数值模拟分析空巷充填支护、木垛支护对工作面过空巷顶板超前断裂、空巷围岩破坏的控制效果，结果显示：充填支护的效果好于木垛支护，其能有效抑制顶板的超前断裂，减小巷道围岩破坏程度。现场确定了高水材料充填与双木垛支护的分区控制措施，现场监测显示，工作面过空巷过程中，液压支架工作阻力处在安全的范围内，工作面能够顺利、安全通过空巷。