GNSS信号估算大气可降雨系统原理及应用进展*
2022-12-06孙一丹郭中华杨昌智毛克彪辛晓平王一帆
孙一丹,郭中华,杨昌智,毛克彪,辛晓平,王一帆,王 平
(1.宁夏大学物理与电子电气工程学院,银川 750021;2.中国农业科学院农业资源与农业区划研究所,北京 100081)
0 引言
全球卫星导航系统(Global Navigation Satellite System,GNSS)是能够向在地球表面的任一地点上或者近地空间环境中任一地点上的用户全天候地提供其速度、时间及三维坐标等数据的空基无线电导航定位系统,也被称为全球卫星导航定位系统。根据GNSS定位原理可以知道在GNSS定位过程中,卫星传出的信号经大气层期间会受到对流层中水蒸汽、电离层以及干燥大气等各种因素的共同作用,使其速度以及路径都会发生改变,所以地面接收机接收的信号会有一定的延迟现象。GPS大气水汽含量探测是一种新兴手段,它可以运用信号的延迟现象定量遥感大气层中的水汽含量,反演结果比较准确,可实现毫米级精度。GPS大气水汽含量探测技术,相对于其他传统的手段而言,具有高精度、高时空分辨率、覆盖面广以及连续观测等特点,能够弥补常规气象探测技术在时间和空间上分辨率不足的缺陷,是我国气象综合探测系统的重要组成部分。
气象灾害发生频繁且很难预料,作为自然灾害的一种,世界上很多国家深受影响。每年洪涝、暴雨、台风等各式各样的自然灾害危及着人们的生命财产安全,我国的国民经济也遭受到了无法弥补的损失。气象探测在人们的生活中至关重要,在科技飞速发展的现代生活中,人类已经能够依靠科技来解决一些以前生活中无法解决的难题,但自然灾害仍是生活中最大的难题之一,严重影响人类的生活。气象探测是气象研究领域中的一门学科,深受大家欢迎,它主要是针对地球大气中大气的现象、化学特性以及物理特性等问题进行研究。目的为研究并介绍能够准确观测出以上问题的手段和方法,并根据所探测出相关数据的波动情况来推测未来的天气变化以及可能来临的气象灾害,进行天气预报,使人们提前对可能出现的灾害采取措施进行预防。这些措施可以有效地减少自然灾害对人们的生活所造成的影响,而且气象信息在很多工作部门起着不可或缺的作用,为人们的工作带来了极大的方便。戴声佩等[1]运用气象站点信息分析了我国华南地区极端降水事件的时空变化特征,通过研究证明大尺度的大气环流对华南地区极端降水的影响明显并且降水事件逐年增加,空间差异十分显著。该研究为华南地区极端降雨事件的未来预测工作做出了巨大贡献。GNSS应用于气象观测领域可以有效地提高数值预报的精度,在气象探测中发挥着不可或缺的作用。利用我国北斗系统进行气象观测系统的建设,既可以在一定程度上提高气象观测技术的自动化水平和准确性,又能推动我国自主卫星导航的终端产品和探测技术在气象观测结果领域中的广泛应用。传统的PWV反演方法多数基于Saastamoinen或者Hopfield等经验模型,不可避免地会引入近似,增大了反演结果的误差,随着机器学习算法的发展利用大量数据进行深度学习可以在较高程度上还原信号延迟量与PWV的相关关系,能够获得较高检测精度的反演模型,将深度学习引入大气可降水量预测也成为了当前研究的热点。
近十几年,研究者们已经重点运用GNSS来研究气象学的相关问题,并已有大量的结果证明此方面的可行性,运用GNSS测量大气水汽的技术正在飞速发展之中。我国已有大量的研究人员投身于相关工作中,虽然我国对于GNSS大气可降水量(PWV)探测技术研究开始的时间晚于其他国家,但我国正在飞速建成特有的北斗卫星导航系统,在北斗卫星以及全球组网的建设下,我国的卫星导航气象观测技术一定会飞速发展,观测水平也会进一步提高。当前研究人员已经进行了BDS不同星历反演大气可降水精度、北斗卫星水汽探测的性能以及BDS/GPS观测PWV反演精度等实验[2-5],证实了北斗系统研究PWV的可行性,能够作为天气预报的参考依据且多系统比单系统的精度高稳定性更好,这对我国的水汽探测工作做出了突出贡献。2020年6月,第55颗北斗导航卫星发射成功,标志着北斗三号(BDS-3)全球卫星导航系统完成全球部署,7月,北斗三号全球卫星导航系统正式开通,北斗事业进入全球服务新时代。相信,在不久的将来,我国的气象探测技术在北斗三号的支持下,精度将会进一步提升,基于北斗三号的水汽探测技术也将为全球的气象观测做出重要贡献。
目前农业遥感等3S空间信息技术是农业数字化的重要手段[6],但我国的北斗系统在气象和农业以及草原等领域的应用才刚刚开始,文章通过阅读和梳理已有的相关研究,对GNSS在大气水汽含量估算方面的数学原理进行了介绍和推导,分析了GNSS信号在估算大气可降雨系统研究中的研究进展以及案例,最后阐述了北斗卫星信号估算大气可降雨系统中目前存在的问题和未来的发展前景。需要强调的是该文中提到的模型以及公式对于GNSS系统均适用,但部分公式的具体参数需要根据不同的导航系统进行修正。
1 GNSS信号估算大气可降雨系统原理
卫星信号在穿透大气层时会发生相应的延迟。假定电磁波在大气层中的传播速度为V1,穿过大气层时产生的延迟量为ΔL,真空中光传播的速度设成C,折射指数设成m,其中m=且与气压、相对湿度、气温等都有一定的联系,大气折射率设成M,接收机接收信号的时间与信号发出时间差设成Δt,且将接收机与卫星之间的间距设为H,信号的真实传播距离设为s,则[7]:
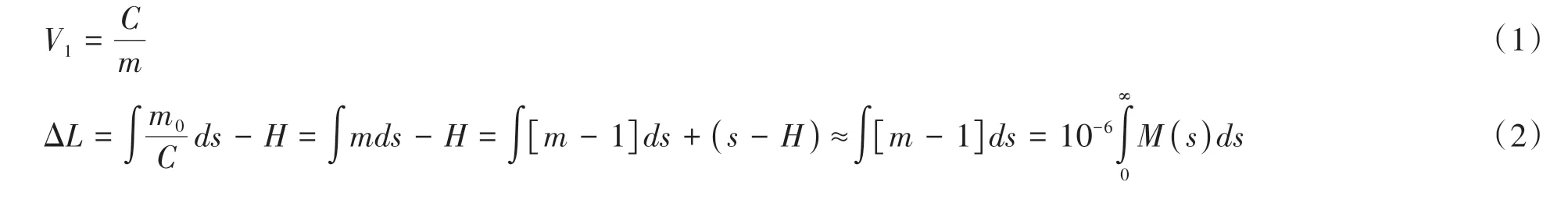
式(1)(2)中M=(m-1)×106,s-H表示信号折射后路径增长的总和,因其占比重较小,大多数情况下可将其忽略不计。其中表示对流层延迟,为校准后的对流层延迟。电离层中发生的延迟现象和对流层中发生的延迟现象共同构成了电磁波传输的信号延迟。资料显示,双频接收机能够减少电离层延迟产生的绝大多数误差,所以我们在实验中使用的接收机大部分都是双频接收机。从式(2)可以看到,大气的折射率能够对对流层中出现的对流层延迟产生影响,而大气湿度、空气温度以及大气气压都与大气折射率有一定的关联。现在已经有很多的研究者对此方面进行了研究,并提供了大气折射率的不同计算公式。Thayer和Boudouris方案的计算精度可以达到0.02%,所以此方案被研究人员广泛采用,计算公式为:[8]
式(3)中,Pd为干空气分压,T为气温;Pv为水汽分压;h1、h2、h3为常数且与折射率相关,这些数值也会因为不同的研究者的选择不同而不同,如表1所示。因Thayer和Boudouris提供的数值精度更为可靠,所以被更多的研究者采用。

表1 不同的大气折射常数值及误差[8] K/hPa
由气体的状态方程可知:

式(4)(5)中,Pv表示水汽分压,Rv表示水汽气体常数,Pd表示干空气分压,Rd表示干空气气体常数,ρv表示水汽密度,ρd表示干空气密度,ρ表示空气密度,因此:

将式(4)(5)以及式(6)带入式(3)可为:

将式(8)代入式(1)中,并进行积分,可得到对流层天顶总延迟量为:

所以对流层延迟也可分为非静力学延迟和静力学延迟。静力学延迟的值会因各地的不同而有些许偏差,基本在2.3m左右(海平面),主要和海拔、经纬度、气压以及温度有关。非静力学延迟(湿延迟)的数值与四季的更替、大气可降水量的多少有一定的关系,是对流层延迟中20%~30%的成分。由上文我们也可以知道中性层延迟与电离层延迟共同构成了大气延迟,且电离层延迟可用双频接收机来消除大部分,所以中性层的大气层延迟为[9]:

式(11)中,Md、Mw分别表示干、湿折射率指数;WD表示湿延迟;HD表示静力学延迟。运用下文提到的方式将大气层延迟转天顶方向上,天顶总延迟ZTD为:

式(12)中,ZWD表示天顶湿延迟,ZHD表示天顶静力学延迟。综上所述,天顶总延迟的关系如图1所示。
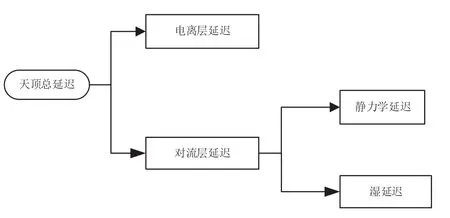
图1 天顶总延迟关系
现在常用GIPSY、GAMIT等软件来处理GPS和北斗系统的数据,这些软件能够高精度的处理数据,求得天顶总延迟参数。大量实验证明天顶静力学延迟有规律可循,可以通过Saastamoinen模型[10]或者Hopfield[11]公式计算获得。其中,ZHD、ZWD在Saastamoinen模型中可以用式(13)表示为:
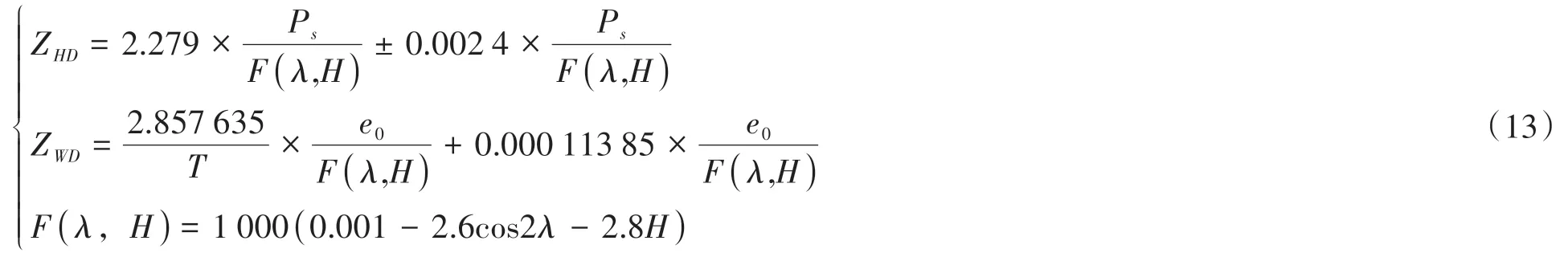
式(13)中,Ps表示测站地表气压,单位为hPa;H表示测站的大地高度,单位为km;λ表示测站的地理纬度;T表示温度,单位为K;e0表示水汽压,单位为mbar。但不足的地方在于大量实验证明,Saastamoinen模型的精度不准,具有厘米级误差。
ZHD、ZWD在Hopfield模型中可以用式(14)表示为:

式(14)中,h表示对流层外边缘的高度,单位为km。研究结果显示,Hopfield模型中ZHD和ZWD的精确值分别在2cm和5cm左右,模型误差与地域也有关系,会存在10cm左右的偏差。以上所介绍两个模型在求ZWD时还要测站的一些有关数据,因水汽在大气层中的变化情况比较明显,会产生厘米级误差,所以在实际情况下一般不会用模型计算ZWD,而是用ZTD-ZHD求出ZWD。
大气水汽含量PWV通常表示的是水柱(高是测站上空到天顶之间的距离)内的水汽全部凝结成液态水时可产生的降水量。PWV与ZWD的关系为式(15):

式(15)中,π表示转换系数,它和对流层的温度存在一定的联系,如式(16):

式(16)中,h2"、h3是大气折射率系数,h2"已在上文介绍过,结合上文可知RV为水汽的气体常数,Tm是影响PWV反演精度的一个重要物理量,被称为加权平均温度,单位为K。在实验中,通常用平均偏差(Bias)、均方根值(RMS)、标准差(Std)以及均方根误差(RMSE)4种精度指标来检验PWV的反演精度以保证实验的准确性和实用性。
多路径效应是产生误差的主要来源,其严重影响了接收机接收信号的精度。误差产生的原因是接收机接收的信号不仅有卫星信号穿过大气层直接投射到接收机的信号,还包括了信号在经过障碍物(地表、高楼大厦、湖水等)后被反射的信号,从而接收机接收到的信号与实际的值有所不同,从而引起误差。多路径效应的产生与信号的传播方向、接收机的摆放位置以及反射系数都有关系,目前的模型还难以完全克服这个影响,因此现阶段研究人员经常会通过在放置接收机时选择合适的位置和在接收机的天线中放置抑径板等方式来减少多路径效应对接收机接收信号产生的影响。
根据对GPS信号研究可知,我国北斗卫星同样可以全天候不间断、穿透云层来向地面传递信号,信号穿透大气层时会发生延迟。大气层分成中性层、电离层以及磁层,其中中性层包括平流层以及对流层。当电磁波穿过中性层、电离层以及磁层时都会对信号产生一定的影响,我们将电磁波在穿过平流层和对流层(中性层)时发生的信号延迟现象统称为对流层延迟,并将电磁波穿过电离层时发生的信号延迟称为电离层延迟。在以后的实验中,可以运用以往研究人员所研究的方法来消除这些信号延迟,保证测得数据的精度。信号在大气层有无水汽的情况下穿过大气层和电离层时的延迟情况有所不同,所以发生的延迟也会有差距,利用这一特点在地面设置一个北斗卫星接收机来接收信号,通过判断接收机接收信号的时间变化来估算大气可降水量的变化结果。根据电磁波传输理论可知,降雨天气大气层中水汽含量升高,北斗卫星传递给地面的信号会受到大气水汽含量的影响,大气水汽含量越多影响越大,传递给地面的信号延迟值越大,通过算法与模型计算延迟量的具体数值,再用相关公式来计算出大气可降水量(PWV)的具体值,结合相关公式即可估算出实际降雨量,从而来完成北斗卫星信号估算大气可降雨研究。下文对相关算法进行了具体介绍。若想提高北斗卫星信号估算大气可降雨系统的精度,可以在地面多安装几个信号接收机,从而在不同角度不同方向来完成实验,用算法进行多次实验使检测结果更有说服力,实验数据更加准确。
根据已有研究可知,利用接收机的精确点位信息可以先反推出电磁波信号穿过对流层产生的延迟量,再定量遥感出对流层延迟。电离层延迟会影响定位的精度,因此为了提高定位精度,一般会通过:(1)同步观测求差法,(2)双频观测值,(3)电离层模型改正等方法来削弱或彻底消除电离层误差带来的影响。
从已有经验可知,接收机接收的大部分电磁波信号都不是从天顶方向传来的,并且在传输路径上的对流层延迟量很难计算,所以研究者们经常采用以下步骤来求解对流层延迟:(1)使用对流层延迟模型中给出的大气延迟先验值,(2)用随机游走的方法估计对流层延迟湿分量,(3)通过映射函数将对流层延迟投影到各颗卫星的信号路径中。常用的映射函数有Boehm提出的VMF1映射函数模型[12]以及GMF映射函数模型[13],具体介绍如下。
(1)VMF1映射函数模型。该模型由Boehm等人构建,具有较高的精确度和可靠性。其中mD(ϑ)和mW(ϑ)的表达式为:

式(17)中,b、c湿项的数值为常数,干项数值是通过ERA再分析资料估计得到的。a的干、湿项的值用射线追踪法计算得到。内插公式可以算得c的干项,表2为内插系数为:

表2 VMF1干项cd的内插系数[14]

(2)GMF映射函数模型。GMF映射模型是Boehm在VMF1的基础上构建的,其精度相对于VMF1模型更高且解决了VMF1模型离不开实际检测气象数据的问题,其中mD(ϑ)和mW(ϑ)的表达式与式(17)相同。
式中,系数bd、bw、cd和cw的数值不变,与VMF1映射函数中的数值一致;用同一计算方式计算系数ad与aw,计算公式为:

年积日doy用来表示余弦函数的变化周期,均值a0是由球谐函数表达式展开至9阶求得:
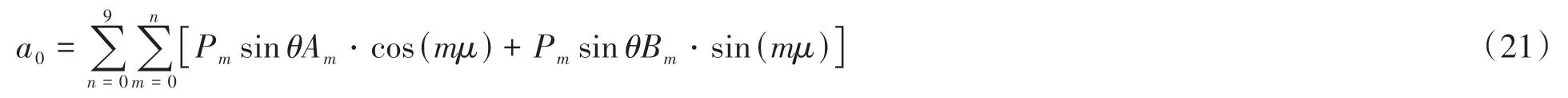
式(21)中,θ是测站的纬度,μ是经度,Am和Bm是球谐函数的系数。
2 北斗/GPS地基检测水汽的试验及应用
现阶段GNSS在不断的发展中已经逐渐趋于成熟,且使用GNSS技术反演大气可降水量也成为了探测大气中水汽的主要方式。现有研究者为改正以往所建立的短时降雨预测模型预测降雨精度不高的缺点,构建了基于径向基(RBF)神经网络的短期降雨预测模型并研究了降雨的相对湿度、PWV等多种相关参数的时变特征[15]。从相关实验的结果可以发现,虽然传统计算方式的出错率和此模型相差不多,但准确率却不如此模型,且该模型可以预测出未来几个小时内大部分的降雨。地基GNSS水汽反演技术是近年来探测大气水汽含量的重要方式,且基于地基GNSS的连续跟踪网可以进行水汽的立体层析,层析技术是依据医学上CT方法发展来的一种检测方法,利用层析技术可以获得大气水汽的分布情况[16]。GNSS层析技术是将观测网内不同路径方向上的水汽值作为层析方程的已知值,并用一段时间内的不同路径上的水汽值建立多个积分方程,求解获得相关的水汽信息[17]。
为进一步满足人们的需要,研究人员在实验过程中引入PPP模式,并探讨在暴雨发生时基于地基GNSS准实时获取的三维层析产品在其中发挥的作用。层析技术的基本原理是将GPS观测网区域按照以往研究者研究的最优分法:(1)截止高度最低为10°,即卫星高度角为10°以下的卫星信号不参与解算。卫星高度角10°以下的卫星容易受到其他环境因素的干扰,使得方程不存在唯一解,不便于解算;(2)站间距小于60km且垂直分辨率为800m[18]分为多个三维网格,把每个网格内的水汽密度看作未知数。假设一段时间内(如半小时内)任一网格内的水汽密度都均匀分布且为常数,则斜路径水汽总量为经过所有网格水汽之和,可用方程表示为:

SWVr是第r条射线路径上的水汽总量;Arijk是射线r在网格(i,j,k)内的长度;Xijk是方程所求未知量,即网格内的水汽密度。实验过程中,将单GPS观测的层析实验结果与北斗/GPS双系统观测的层析实验结果进行对比,分析结果可以发现,虽然单系统的被穿过的网格数不如双系统的数目多,但双系统的精确度并没有十分明显的提高。之所以这样是因为所选北斗卫星的高度角太高运行缓慢,在实验期间还未来得及对低层大气的层析实验产生影响且层析区域小使得大部分的射线进入不到层析区域,致使层析结果产生误差。最重要的是,在实验过程中,会设置截止高度角来降低噪声以及周围环境产生的影响,但这会使对应的观测值也被消除,并且三维水汽层析的过程中,并不是所有的射线都能从正面穿过网格,而只有从网格正面穿过的射线才会对层析方程产生影响,也并不是每一个网格点都会有射线穿过。所以可以通过添加约束条件(垂直约束和水平约束)的方式来解决上述原因造成的层析方程的问题。对于垂直约束,大气水汽与高度呈负相关,由张豹等在2017年的研究可知,指数函数并不能很完美的表达湿折射率,因其不存在极值,所以没办法表示出最大值[19]。而高斯函数与之相比,其曲线变化丰富,能够符合实际情况的表示出湿折射率的垂直分布情况。对于水平约束,水汽在水平空间上的变化一般较为平缓,可使用均值滤波或者高斯加权函数进行平滑约束。但也因为约束条件的设置,三维层析的方法在空格以及观测数据的利用率上都有一定的局限性,为了进一步改善PPP探测PWV的性能,李宏达[20]等提出了采用多系统组合PPP,将GPS、BDS、GLONASS、Galileo组合PPP进行PWV反演,并与GPS PPP、GPS/BDS组合PPP以及GPS/GLONASS组合PPP等进行对比,实验结果显示GCRE初始化时间相比于G、GC、GR分别缩短了33%、26%以及20%,且同一测站下GCRE有比其他方案精度更高的ZTD估值,均方根误差有所减少以及其测得的PWV的变化趋势与RS/PWV基本一致,证明了将4种系统结合起来的PPP估计ZTD的初始化时间更短,并且精度更高,测得的PWV数值更加准确,在水汽探测方面的效果更好,更适合应用于天气预报当中。2021年张庆志[21]等利用GPT2w模型计算层析区域初始场,并引入比例系数联合水汽密度初值估计层析区域外测站信号在区域内水汽含量,构建了一种可以将层析区域外一定范围内的GNSS测站数据利用起来的方法,相对于传统的层析方法有效提高了射线利用率以及层析结果的精度和可靠性,进一步完善改进了我国的大气可降雨系统,不过此方法也仅能利用层析区域外一定范围内的测站。
2020年黄逸宇等[22]提出了用改进的BP神经网络模型预测大气可降水量的实验方法,在原有实验的基础上将大气可降水量的历史数据进行迭代,迭代结果作为初始化参数后继续进行原有实验,此初始化参数使实验结果更加准确,有效地提升了预测精度。BP神经网络的基本原理以及流程如图2所示。

图2 BP神经网络的基本原理流程
其中每一层节点输入层的计算公式为:

式(23)中,n代表层数;φij,ϑj分别代表了第n层的权值和阈值;αi为输入数据的中间参数,其对应的输出层为:
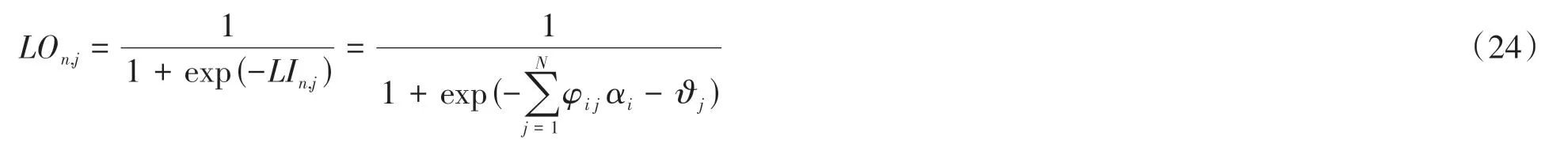
式(24)中,LOn,j表示输出层计算后得到的PWV值,f(x)=是最常用的激活函数,其作用是将数据区间映射到[0,1]内。
现在,权值更新表达式为:

式(25)中,α(t)为误差项;β(t)为输出量;μ为学习效率。
改进的BP神经网络则是将传统的权值和阈值进行迭代计算后,能够得到的对应时刻改进模型的初始化参数φ"和ϑ",新的PWV模型使用新的参数建立。黄逸宇等[22]运用改进的BP神经网络提升了GPS-PWV的反演精度,实验过程中将经过归一化处理的探空站点和GPS站点的经纬度坐标x,y和大地高度h、年积日DOY值以及加权平均温度Tm作为输入参数,把PWV作为输出值。同样该模型也可以用于北斗信号进行大气可降水量反演,同时为了进一步提高检测精度,可以在输入层增加信号延迟w这一属性来扩充神经网络的维度,用来反演大气可降水量的神经网络结构如图3。此方法是根据改进神经网络的GPS测大气可降水量方式改进而来,根据GPS的实验可以推测此方法的可行性,但具体实验结果还有待进一步考证。

图3 反演大气可降水量的神经网络结构
随着我国北斗系统的逐步建成,关于北斗卫星进行水汽探测的相关实验已经有越来越多的研究者们进行了探索验证,王海深等[23]将探空数据测得的PWV与北斗系统和GPS系统测得的PWV进行了比较,实验结果显示,BDS-PWV高于GPS-PWV,且在北斗系统和GPS两种系统之间的标准偏差为2.5~2.8mm,系统误差为2~3.3mm。从结果可以看出,此实验证实了北斗水汽探测的可行性,也说明了尽管GPS、北斗系统都和地面探空系统具有良好的一致性,能够非常好地反映大气水汽的变化规律,但由于北斗系统比GPS系统的误差范围更大,还需要进一步提高精度。
3 结语及展望
探测大气实际降水量的研究是气象监测中重要研究方向之一,水汽是降水的先决条件,当大气水汽遇冷时迅速凝结,增大到能克服空气阻力和上升气流的顶托且在降落时不能被完全蒸发便形成了降水。降水多发生在水汽含量达到峰值的附近时刻,通过对水汽含量变化的监测能够对降水进行一个较为准确的预测。利用大气水汽对定位信号的延迟作用可以反演获得大气可降水量PWV的信息,作为一个衡量大气水汽含量的参数,通过对PWV的研究就可以反过来确定大气水汽含量的信息。另外由杨军建等[24]对水汽含量和降水序列的对比可以知道大气水汽含量和实际降水量之间存在着明显的相关关系,且利用定位信号反演获得的PWV数据同探空数据对比也呈高度一致,差值均值只有0.42mm。通过对当前研究的梳理可知,利用GPS测量大气可降水系统的相关研究已经趋于成熟,可以在一定程度上较为精准地确定PWV值,并且可以对大气实际的降水量做出预测。同时PWV的变化趋势也能展现出降雨的变化趋势,这为人类预防洪水、山体滑坡等自然灾害提供了重要技术支撑。
北斗卫星工程近年来已成为我国发展的重中之重,其在各个领域的应用需要进一步深入。GPS卫星信号在大气水汽监测方面的模型和应用为气象研究增添了新的方式,不同的导航系统均具有相似之处,借鉴GPS的导航研究体系,可以研究适合于北斗系统的新应用模式。另外将GPS系统与北斗系统信号数据相结合,对机器学习模型输入参数维度进行扩充结合深度学习方法来提高反演精度的试验也可以作为下一步的研究方向。通过改进模型和算法,基于我国北斗卫星信号可以进一步提高大气可降水量的测量精度,为气象预报和农业生产带来更多的技术支撑。
