基于Smith PSO-Fuzzy PID的营养液EC值调控模型研究
2022-12-06王永涛刘坚李家春陈波李擎
王永涛,刘坚,李家春,陈波,李擎
基于Smith PSO-Fuzzy PID的营养液值调控模型研究
王永涛1,2,刘坚1*,李家春3,陈波3,李擎3
(1.湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082;2.贵州省水利科学研究院,贵阳 550002;3.贵州大学 机械工程学院,贵阳 550025)
【目的】探寻多通道水肥控制装置的精准调控与控制技术。【方法】本文设计了由工业铝型材机架、主管路系统、吸肥系统、混肥系统、检测系统、控制系统及施肥系统等7部分构成的多通道水肥一体化装置,构建了基于PSO优化Fuzzy PID的营养液值调控模型并引入Smith预估当中(Smith PSO-Fuzzy PID)。并以目标值2 mS/cm为例,采用MATLAB分别进行了传统PID、模糊PID(Fuzzy PID)和Smith PSO-Fuzzy PID仿真。【结果】采用Smith PSO-Fuzzy PID控制方法,稳态时间约为47 s,超调量约为4.83%,系统值稳定在1.987~2.080 mS/cm。【结论】与传统PID和Fuzzy PID相比,本文基于PSO优化Fuzzy PID的水肥装置Smith控制系统,具有更快的响应速度,更高的精度。
Smith;PSO;模糊PID控制;水肥一体化
0 引言
【研究意义】农业生产过程中的精准灌溉和精准施肥,不仅可以提高农产品的产量和质量,还可以有效解决过度施肥带来的环境问题,符合我国生态绿色发展理念。然而,水肥精准控制技术的发展仍然滞后,制约了农业现代化的发展。本研究对于提高水肥装置的控制精度,提高农业规模化生产的质量和效益具有重要意义。【研究进展】目前,水肥装置控制方法主要有以下4种:①模糊控制:李加念等[1]通过研究得出施肥装置最佳入口压力范围为0.15~0.25 MPa;刘永华[2]设计了温室灌溉施肥一阶惯性系统的传递函数,并采用Matlab仿真,试验验证上升时间62 s,稳态时间450 s;何青海等[3]基于LabVIEW平台开发了水肥一体化系统和模糊控制器,实现了灌溉、施肥、施药及水肥一体化,系统具备控制、监控和信息查询等功能;牛寅[4]提出了一种能够实现定性概念和定量描述之间不确定转换关系的云模型。采用该云模型与模糊控制结合,提出了控制的VFPI和pH值控制的CVFPI智能控制方法;②模糊控制与PID结合:王孝龙[5]设计了模糊PID控制器,实现了对水肥精准配比的控制;张育斌等[6]基于值和pH值,应用模糊PID控制技术,开发了精量水肥灌溉控制系统;王海华等[7]采用PI与模糊分段调控策略,较好地解决了水肥调控的滞后和不稳定问题;李莉等[8]分析了封闭式栽培系统的实际需求,设计了营养液调控二次混肥结构,并建立了营养液调控动态过程的数学模型。同时,还设计了PI控制算法,试验验证系统稳态时间为100 s,超调量3%,控制性能优良;③PID与Smith结合:袁洪波等[9]设计了一种营养液制备的装备及数学模型,采用基于增量式PID算法和改进Smith预估器的营养液调控算法,加快了系统的响应速度,提高了控制精度;④机器学习:孙锋申等[10]提出了小波神经网络模糊控制的水肥一体化研究思路;刘军涛等[11]采用RNN循环神经网络控制算法,基于历史农业信息和专家意见,实现农作物的长势与生长周期的自动控制灌溉、施肥的精量灌溉。总体来讲水肥装置控制方法呈不断向前发展的趋势。【切入点】综上所述,在水肥一体化系统中,采用PID经典控制与模糊控制结合应用较为广泛。但模糊控制的比例因子的选取随意性较大,影响了系统的推广应用。【拟解决的关键问题】本文利用PSO对模糊控制方法的比例因子Pd进行优化,与传统PID和Fuzzy PID相比,系统具有更快的响应时间和更高的控制精度。
1 装置结构及工作原理
1.1 结构组成
水肥一体化装置设计的目的是根据作物的种类、生育期需肥量进行精准灌溉和精量施肥。水肥一体化装置的工作过程是一个肥料母液与水混合的动态过程,具体为:持续向缓冲混肥桶内加入水w和肥料母液NS,同时通过助肥泵向灌区提供制备完成的目标营养液out进行施肥。制备过程与施肥过程同步进行。农作物电导率()范围一般在0.8~2.5 mS/cm之间,电导率()误差范围应不超过±0.8 mS/cm,要求营养液制备具有很高的效率和即时性[12]。根据实际生产需要,可配置为氮(N)、磷(P)、钾(K)3个施肥通道及农药(FC)灌施通道[13]。
国内外水肥一体化装置分为单通道和多通道,其中多通道可设定配肥比例,具有水肥效率高的特点,故本文设计了如图1所示的多通道水肥一体化装置。该装置主要由工业铝型材机架、主管网系统、吸肥系统、混肥系统、检测系统、控制系统及施肥系统等7部分构成,见表1。
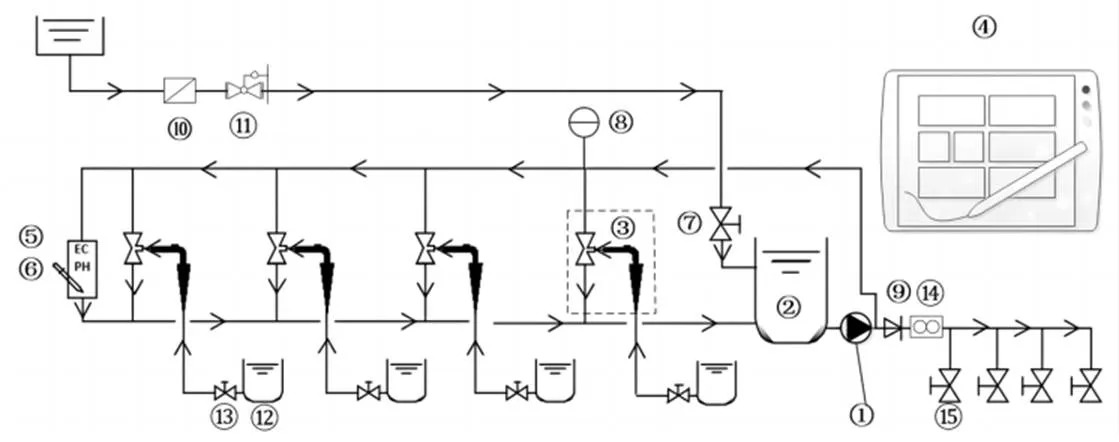
注 ①助肥泵;②缓冲混肥桶;③文丘里射流器;④控制箱(包括控制器、操作屏等)系统;⑤EC传感器;⑥pH传感器;⑦浮球阀;⑧压力表;⑨止回阀;⑩主管过滤器;⑪减压阀;⑫储肥桶;⑬注肥阀;⑭流量计;⑮施肥阀。

表1 水肥一体化装置组成
营养液制备过程为:①水w通过有压管道连续不断地注入缓冲混肥桶2中,同时助肥泵1从缓冲混肥桶2底部抽取营养液,一部分营养液通过连接管路经过文丘里射流器3后F再次注入缓冲混肥桶2;另一部分营养液out通过管网进入灌区进行施肥;②在文丘里效应的作用下肥料母液NS被持续吸入文丘里射流器3中,并通过文丘里射流器3后F最终注入缓冲混肥桶2。肥料母液NS和水w在文丘里射流器3内进行第一次混合,在缓冲混肥桶2内进行第二次混合,形成2次混合模式。肥料母液NS和水w混合的均匀度和制备效率均大幅提高,水肥一体化装置工作原理见图1。
1.2 工作原理
本文水肥一体化装置采用对注肥阀的开关控制,动态调节肥料母液(N)、磷(P)、钾(K)与水w的混合比例,实现的精确控制。本文设定注肥阀的工作频率为6 Hz,多通道水肥一体化装置入口压力为0.25 MPa[14],注肥阀一直打开的情况下(占空比为100%)的初始工作条件,构建水肥控制模型,分析系统的工作特性。图2为文丘里射流器工作原理图。

注 P1、v1、Q1、d1分别为文丘里射流器进水口的压力、流速、流量、直径;P0、v0、Q0、d0分别为文丘里射流器喉部的压力、流速、流量、直径;P、v、Q、d分别为文丘里射流器吸肥口的压力、流速、流量、直径;P2、v2、Q2、d2分别为文丘里射流器营养液出口的压力、流速、流量、直径。
文丘里射流器流量、流速、截面积、水压之间的关系式(1)—式(2):

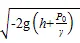
式中:为射流器吸取肥液的流量(m3/h);为流量系数,与文丘里射流器的形状有关,通常取0.6~0.65;为射流器吸肥口截面积(m2);1为文丘里射流器进水口的压力(Pa);2文丘里射流器营养液出口的压力(Pa);为流体的密度(kg/m3);g为重力加速度(m/s2);为施肥罐液面到射流器的垂直高度(m),在上时取负,在下时取正;0为射流器喷嘴处压力(Pa);为液体肥料的比重(N/m3)[15-16]。
2 装置控制模型
由于文丘里射流器在吸肥的同时进行混肥,可视为在缓冲混肥桶2中增加了虚拟的混肥容积F,混合过程为平推流(塞流)和理想搅拌混合的结合。整个系统为二阶滞后系统,由式(1)计算得:w1 L/s,F=0.05 L/s。由式(2)得NS0.01 L/s。本文以10 L混肥桶为例(工作有效容积为9 L)开展研究,系统的传递函数为式(3),其中T=5 L,F=4 L[17-19]。

式中:c()为期望营养液电导值率的输出值(mS/cm);NS()为肥料母液流量的输出值(L/s);2为增加文丘里射流器后形成的二阶系统增益(L/s);F为在文丘里射流器中营养液制备过程的时间常数(s);F为增加文丘里射流器后增加的预混合容积(L);1为混合系数,本文1=0.8。对于平流模式,1=0,对于理想搅拌模式,1=1;r为系统的延迟时间(s),T为混肥桶有效混合容积(L);F为流入文丘里射流器的液体流量(L/s);W为注入混肥桶的水流量(L/s);为肥料母液在缓冲混肥桶的混合滞后及测量滞后时间,包括液体在管道中的流动时间和混合时间(s);为新的滞后时间(s);NS≤F<w,NS为注入肥料桶中肥料母液的流量(L/s)。
3 PSO-Fuzzy PID控制方法
3.1 PSO算法原理
假设维空间中有个粒子,x表示粒子的位置,v表示粒子的速度,表示粒子个体经过的最好位置,表示种群所经历的最好位置,在每次迭代中,粒子的第维速度根据下列公式更新:

粒子的第维位置根据下列公式更新:

式中:为第次迭代粒子飞行速度矢量的第维分量;为第次迭代粒子位置矢量的第维分量;1和2为学习因子,取值范围在[1.2,2.0];和为在[0,1]区间的随机数;为惯性权重,描述了粒子的惯性对于速度的影响,其取值可以调节粒子群算法的全局与局部寻优的能力;max为事先确定的正常数,限制速度的变化范围。当迭代次数达到最大迭代次数或迄今为止搜索到的最优位置满足最小适应度阈值时终止迭代[20]。
3.2 PSO优化Fuzzy PID
系统采用输入电导率的误差()、电导率误差的变化率(),输出∆p、∆、∆d进而调节PID控制器的3个参数,提高系统动态响应速度,增强系统对于土壤水肥变化的适应性。
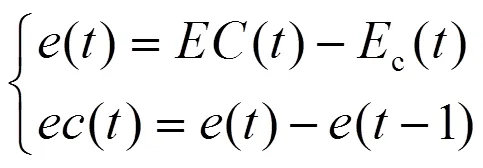
式中:()为实际测得营养液电导率;c()为目标电导率;(-1)为t-1时刻电导率的误差。定义目标函数为误差绝对值积分型,既考虑了误差的绝对值的大小,又增加了时间的权重,见式(7):

式中:为目标函数;为时间权重;|()|为误差绝对值。
在常规的PID基础上,通过模糊化处理、模糊控制规则、模糊决策及解模糊化处理等环节,输出量为PID控制器的3个输入修正参数∆p、∆、∆d。当()、()按不同规律变化时,并结合人工经验制定出合理的模糊规则。并根据模糊规则对PID各参数进行在线修改,从而使系统性能达到最佳。之后,参照模糊规则展开模糊推理,推理结果经解模糊化处理,清晰量∆p、∆、∆d再经过PSO优化的量化因子(或比例因子)计算作为输出量,最后经过p、、d得到该采样时刻的实际控制量,最终确定电磁阀的开启时间[21],图3为PSO-Fuzzy PID控制系统框图。
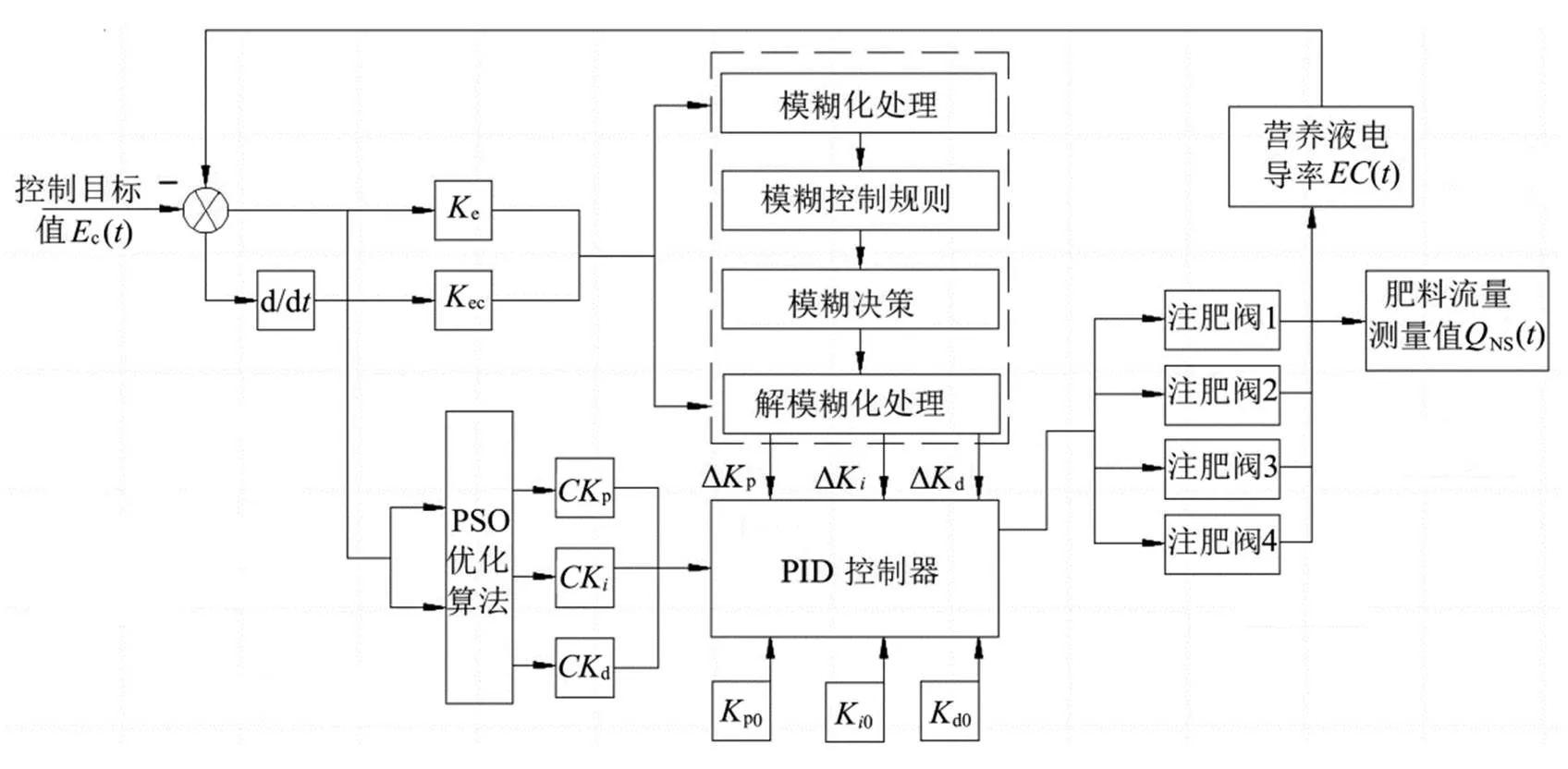
图3 PSO-Fuzzy PID控制系统
3.3 输入输出模糊变量及论域
根据王海华等[7]的研究多通道水肥一体化装置营养液电导率从0 mS/cm升高到2.5 mS/cm用时约为180 s,输入()的基本论域为:[-0.8,0.8],()的基本论域为:[-0.8,0.8],设定()的模糊论域为:[-4,4],()的模糊论域为:[-4,4],则输入量、的量化因子e、ec;输出∆p、∆K、∆d的模糊论域为[-3,3]。

式中:e、ec分别为输入量、的量化因子。
通过单独PID控制器分析,PID的初始值设为p0=8,0=0.01,d027,PID控制器的3个参数p、i、d及其对应的输出比例因子为式(9)。

式中:p、、d分别为PID控制器的3个参数;pd别为PID控制器的比例因子;∆p、∆、∆d分别为模糊控制器的输出;p00d0分别为PID的初始值。
3.4 模糊控制器的控制表
根据系统运行参数,选取偏差、偏差变化为输入,为输入变量、的模糊集合,输出为增量∆p、∆、∆d。输入、输出语言变量均取{NB,NM,NS,ZO,PS,PM,PB}(分别代表负大、负中、负小、零、正小、正中、正大)7个模糊值,对应{-3,-2,-1,0,1,2,3}。根据所述原则和系统的经验知识,制定表2—表4的模糊控制规则。
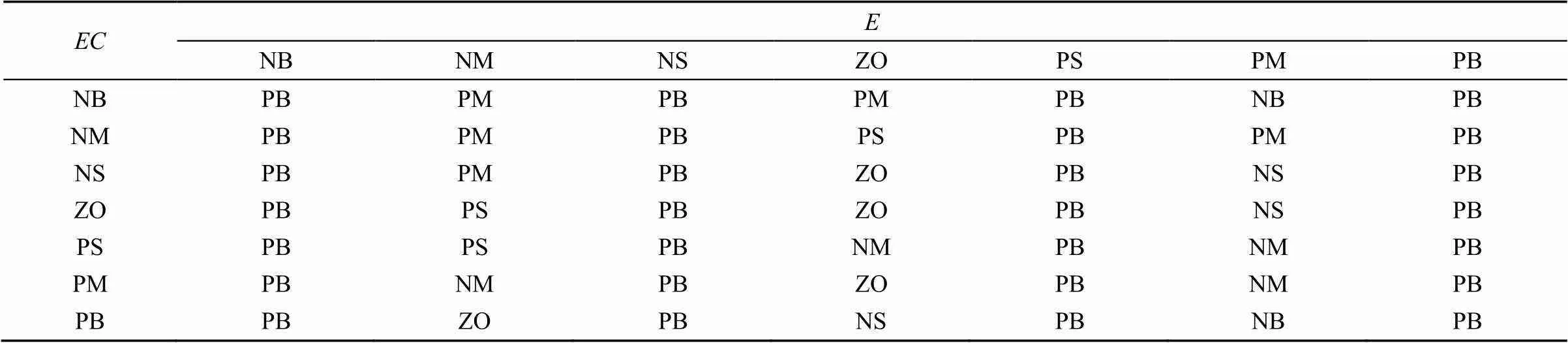
表2 参数∆Kp模糊控制规则
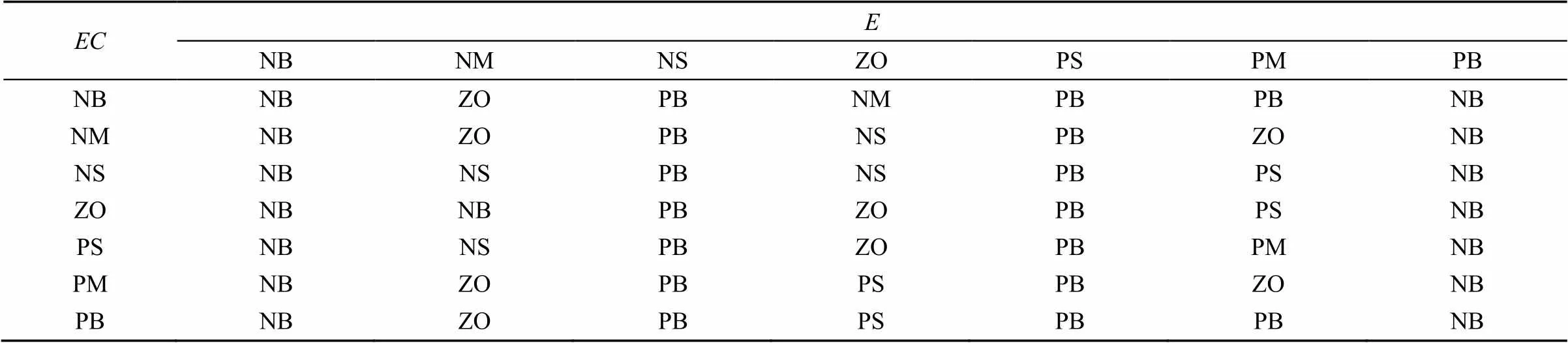
表3 参数∆Ki模糊控制规则

表4 参数∆Kd模糊控制规则
3.5 模糊推理系统的构建
采用MATLAB的模糊推理系统(FIS)编辑器创建一个2输入3输出的mamdani推理模糊控制器,输入变量命名为偏差及其变化率、,对应的模糊集合;输出变量命名为PID比例、积分、微分系数的增量∆p、∆、∆d。
1)模糊推理
对于∆p、∆、∆d共生成49条控制规则,命名为“fuzzypid”。
Rule1:若偏差为NB,偏差变化为NB,则输出∆p为PB。
Rule2:若偏差为NM,偏差变化为NB,则输出∆p为 PB。
Rule3:若偏差为NS,偏差变化为NB,则输出∆p为PB;……。
Rule49:若偏差为PB,偏差变化为PB,则输出∆p为NB。
2)定义各模糊子集的隶属函数
通过试验确定、模糊论域隶属度函数,当、分别为[-4,-2]、[2,4]时,采用zmf隶属度函数;当、分别为[-3,-3]时,采用trimf隶属度函数。∆p、∆i、∆d在整个模糊论域上均采用trimf隶属度函数时控制效果较好,图4—图5为本文构建的模糊控制器属性图及三维图[22]。
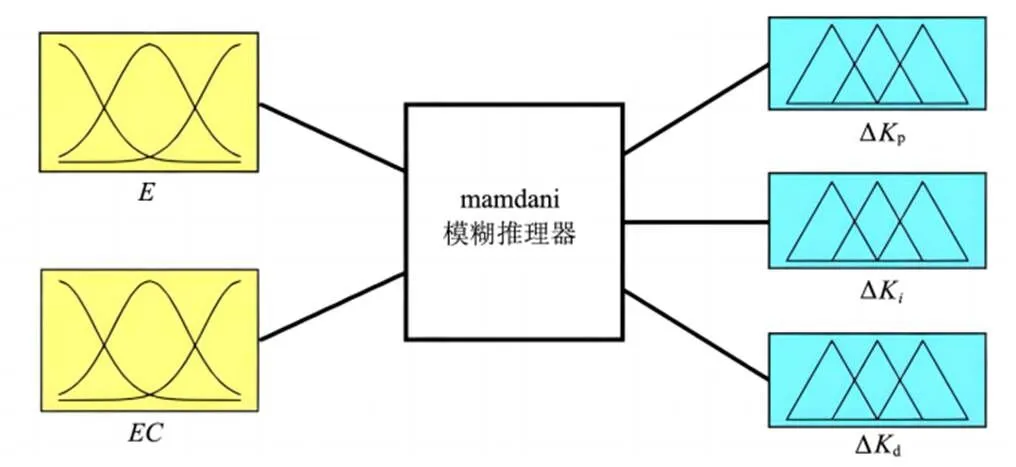
图4 模糊控制器属性图

图5 模糊控制器三维图
3)反模糊化
利用面积重心法对控制器的模糊输出进行反模糊化,就可以得到∆p、∆、∆d的模糊论域上的值,面积重心为式(10):
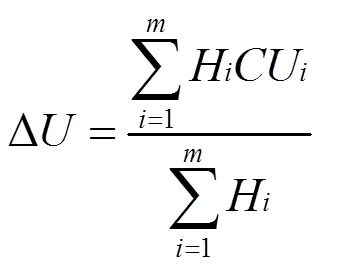
式中:为隶属函数为三角形面积重心;为每个规则输出面积的高;为每个规则输出重心的横坐标。
4 Smith PSO-Fuzzy PID仿真与分析
4.1 Smith控制算法原理
在大迟滞系统中,常采用补偿方法来优化控制,其按照控制对象特性设计出一种模型加入反馈控制系统中,来补偿系统过程控制的动态特性。常用的为Smith先生于1959年提出史密斯预估器,其主要原理是预先估计出控制的动态模型,然后将Smith预估器并联在被控对象上,让其对过程中的纯滞后特性进行补偿,预期是将被延迟的时间的被控量提前送入到控制器中,让其能提前做出反应,这样就通过补偿器的方法来消除滞后带来的影响。在实际生产中,如果在模型匹配的条件下能够有效减少超调、可以获得比较好的控制效果。
在未进行Smith预估补偿情况下,系统闭环传递函数为:
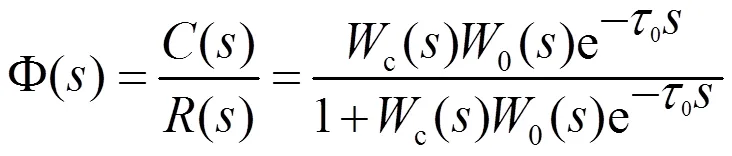
故其闭环特征方程式为:
(12)

可得,Smith补偿器方程为:
(14)
于是,Smith补偿系统又可表示为图6。

图6 Smith预估补偿系统一般型框图
式(11)—式(14)中:c()为PID调节器;0()e-τ0为被控对象的传递函数模型,其中0()为不包括纯滞后时间0的对象模型;s()为Smith预估补偿器。
4.2 Smith PSO-Fuzzy PID仿真与分析
PSO适应度参数=0.6、1=2、2=2、=10、=3、最大迭代次数=5、=0.1、max=1。采用MATLAB的Simulink环境进行仿真,输入=2 mS/cm的阶跃信号,控制对象的传递函数为式(3),通过设置相同的初始值,同示波器输出目标阶跃信号,图7为Smith PSO-Fuzzy PID EC调控模型,图8为Smith PSO-Fuzzy PID方法比例因子,由图8可以看出,Smith PSO-Fuzzy PID方法优化后的比例因子为p=1.823 1、=0.11、d=0.108 6。图9为不同控制方法 MATLAB仿真图。

图7 Smith PSO-Fuzzy PID控制系统模型

图8 Smith PSO-Fuzzy PID方法比例因子
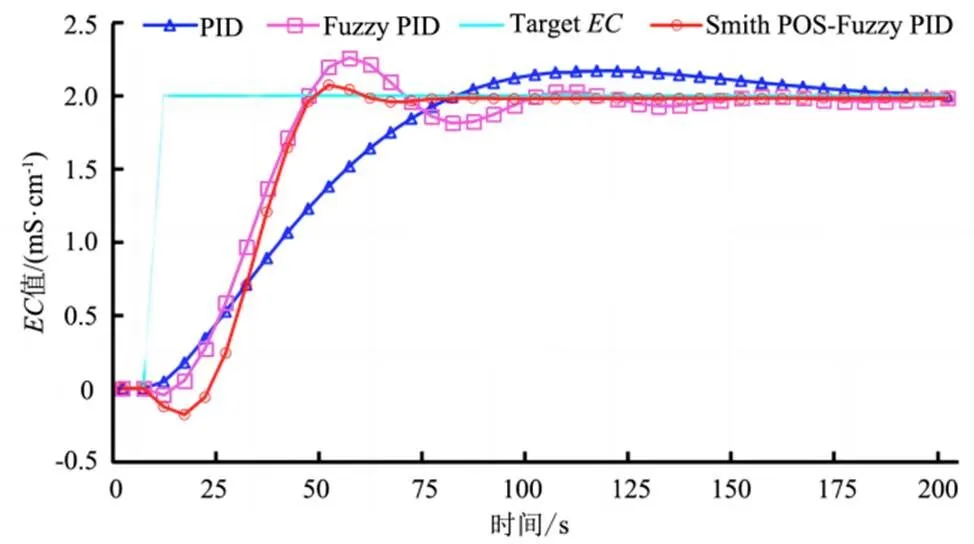
图9 不同控制方法 MATLAB仿真图
从图9可以看出,Smith PSO-Fuzzy PID控制稳态时间约为47 s,超调量约为4.83%,系统值稳定在1.987~2.080 mS/cm;而Fuzzy PID稳态时间约为52 s,超调量约为10.7%,系统值稳定在2.20~1.97 mS/cm;传统PID稳态时间约为189 s,超调量约为8.45%,系统值稳定在1.99~2.12 mS/cm,且震荡较大。对比仿真结果表明,本文Smith PSO-Fuzzy PID比其他2种控制方法,具有更快的响应速度,更高的精度。
4.3 系统仿真模型验证
进一步输入值分别为1、1.5、2、2.5 mS/cm时,进行仿真模型验证。由表5可以看出,的波动幅度为0.003~0.164 mS/cm,稳态时间为47~78 s、超调量为4.69%~5.27%,可以满足农业生产快速、准确的实现水肥一体化的要求。

表5 不同EC设定值Smith PSO-Fuzzy PID的试验对比
5 讨论
营养液值调控为水与肥耦合的过程,具有时滞性、动态性、非线性等特点,精准调控技术难度较大,控制精度通常较低。总体来讲,目前控制方法从模糊控制、模糊控制与PID结合、PID与Smith结合以及机器学习呈不断向前发展的趋势。
一方面,模糊控制无须建立精确地控制模型,对于非线性系统优势较为明显,但模糊控制比例因子的选取依靠经验随意性较大,系统上升时间、稳态时间均较大,影响了推广应用。而另一方面,模糊控制与PID结合、PID与Smith结合一定程度上提高了系统的控制性能,但对于时滞、动态的水肥调控系统,PID控制存在过渡时间与超调量之间的矛盾,精度难以满足要求。同时,PID参数的整定需要凭借经验和反复调试,工作量较大。此外,机器学习控制方法仍停留在理论研究层面,实际应用还有较大差距。
本文针对混肥桶式注肥模式开展了营养液值调控模型研究,基于PSO优化方法、纯滞后的Smith控制算法、模糊控制与PID结合,构建了基于Smith PSO-Fuzzy PID的营养液值调控模型。以输入=2 mS/cm目标阶跃信号为例,将Smith PSO-Fuzzy PID、Fuzzy PID、传统PID 3种控制结果进行比较,得到本文Smith PSO-Fuzzy PID控制稳态时间约为47 s,超调量约为4.83%,系统值稳定在1.987~2.080 mS/cm;而Fuzzy PID稳态时间约为52 s,超调量约为10.7%,系统值稳定在2.20~1.97 mS/cm;传统PID稳态时间约为189 s,超调量约为8.45%,系统值稳定在1.99~2.12 mS/cm,且震荡较大。仿真结果表明,本文Smith PSO-Fuzzy PID比其他2种控制方法,具有更快的响应速度,更高的精度。进一步输入值分别为1、1.5、2、2.5 mS/cm,得到值的波动幅度为0.003~0.164 mS/cm,稳态时间为47~78 s、超调量为4.69%~5.27%,从仿真的角度提出了营养液值调控新的方法和思路,可以满足农业生产快速、准确实现营养液值调控的需求,具有一定的创新性与实际应用价值。
采用PSO优化水肥精准调控系统可快速找到最优的比例因子pd,消除PID参数整定的影响。同时,采用Smith预估补偿滞后过程,通过补偿器的方法消除滞后带来的影响。并将Smith、PSO与Fuzzy PID结合,能够有效减少超调、提高控制系统的性能,获得比较好的控制效果。但针对理想仿真模型的研究与实际系统还存在一定的差距,还需要搭建实际的水肥调控系统进行进一步的田间试验,分别对不同值及不同的控制方法进行实测,增加实际产品验证数据,以进一步说明所构建控制模型的优良性能。
6 结论
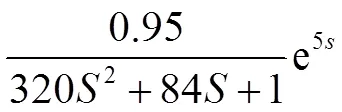
2)在相同初始条件下,当输入=2 mS/cm时,Smith PSO-Fuzzy PID方法优化后的比例因子为p=1.823 1、=0.110 0、d=0.108 6,稳态时间约为47 s,超调量约为4.83%,系统值稳定控制在1.987~2.080 mS/cm,与Fuzzy PID和传统PID控制,系统控制性能优良。
3)在输入1、1.5、2、2.5 mS/cm时,使用Smith PSO-Fuzzy PID分别进行系统仿真模型验证,值的波动幅度为0.003~0.164 mS/cm,稳态时间为47~78 s、超调量为4.69%~5.27%,可以满足水肥一体化快速、准确的要求。
[1] 李加念, 洪添胜, 冯瑞珏, 等. 基于脉宽调制的文丘里变量施肥装置设计与试验[J]. 农业工程学报, 2012, 28(8): 105-110.
LI Jianian, HONG Tiansheng, FENG Ruijue, et al. Design and experiment of Venturi variable fertilizer apparatus based on pulse width modulation[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(8): 105-110.
[2] 刘永华. 温室精准灌溉施肥系统关键技术研究[D]. 南京: 南京农业大学, 2015.
LIU Yonghua. Research on key technologies of precision irrigation fertilization system for greenhouse[D]. Nanjing: Nanjing Agricultural University, 2015.
[3] 孙宜田, 李青龙, 孙永佳, 等. 基于模糊控制的水肥药一体化系统研究[J].农机化研究, 2015, 37(8): 203-207.
SUN Yitian, LI Qinglong, SUN Yongjia, et al. Study on the system of irrigation, fertilization and spraying based on fuzzy control[J]. Journal of Agricultural Mechanization Research, 2015, 37(8): 203-207.
[4] 牛寅. 设施农业精准水肥管理系统及其智能装备技术的研究[D]. 上海: 上海大学, 2016.
NIU Yin. Research of precision fertigation control system and equipment technology in facility agriculture[D]. Shanghai: Shanghai University, 2016.
[5] 王孝龙. 水肥精准配比控制系统研发[D]. 杨凌: 西北农林科技大学, 2018.
WANG Xiaolong. Research and development of precision fertilizer proportioning control system[D]. Yangling: Northwest A & F University, 2018.
[6] 张育斌, 魏正英, 朱新国, 等. 精量水肥灌溉系统控制策略及验证[J]. 排灌机械工程学报, 2017, 35(12): 1 088-1 095.
ZHANG Yubin, WEI Zhengying, ZHU Xinguo, et al. Control strategy for precision water-fertilizer irrigation system and its verification[J]. Journal of Drainage and Irrigation Machinery Engineering, 2017, 35(12): 1 088-1 095.
[7] 王海华, 付强, 孟繁佳, 等. 模糊与PI分段调控肥液EC的优化设计与试验[J]. 农业工程学报, 2016, 32(15): 110-116.
WANG Haihua, FU Qiang, MENG Fanjia, et al. Optimal design and experiment of fertilizer EC regulation based on subsection control algorithm of fuzzy and PI[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(15): 110-116.
[8] 李莉, 王俊衡, 孟繁佳, 等. 基于二次混合机构的营养液调控模型与PID算法实现[J]. 农业工程学报, 2016, 32(22): 100-106.
LI Li, WANG Junheng, MENG Fanjia, et al. Model and PID algorithm realization of nutrient solution control based on two-step fertilizer mixing system[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(22): 100-106.
[9] 袁洪波, 李莉, 王俊衡, 等. 温室水肥一体化营养液调控装备设计与试验[J]. 农业工程学报, 2016, 32(8): 27-32.
YUAN Hongbo, LI Li, WANG Junheng, et al. Design and test of regulation and control equipment for nutrient solution of water and fertilizer integration in greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(8): 27-32.
[10] 孙锋申, 魏燕, 马伟顺, 等. 基于小波神经网络的水肥一体化控制技术[J].南方农机, 2019, 50(8): 12-13.
SUN Fengshen, WEI Yan, MA Weishun, et al. Southern Agricultural Machinery[J]. China Southern Agricultural Machinery, 2019, 50(8): 12-13.
[11] 刘军涛. 基于深度学习与物联网的水肥一体化云系统研究[D]. 邯郸: 河北工程大学, 2018.
LIU Juntao. Research and realization of integrated cloud system based on deep learning and Internet of Things[D]. Handan: Hebei University of Engineering, 2018.
[12] 范丽. 营养液电导率传感器及测量系统的设计[D]. 南京: 南京农业大学, 2016.
FAN Li. Design of nutrient solution conductivity sensor and measurement system[D]. Nanjing: Nanjing Agricultural University, 2016.
[13] 冀步方. 智能深液栽培和滴灌施肥桌面系统研究与实现[D]. 武汉: 华中农业大学, 2015.
JI Bufang. Research on simulation for intelligent irrigation and fertilization[D]. Wuhan: Huazhong Agricultural University, 2015.
[14] 周良富, 金永奎, 薛新宇. 电磁阀开关模式下文丘里施肥器吸肥特性研究[J]. 农业工程学报, 2019, 35(22): 277-284.
ZHOU Liangfu, JIN Yongkui, XUE Xinyu. Suction characteristics of venturi injector in solenoid valve switch ON & OFF mode[J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(22): 277-284.
[15] 高波, 寇子明. 基于Fluent射流器负压产生机理的研究[J]. 煤矿机械, 2012, 33(7): 77-79.
GAO Bo, KOU Ziming. Mechanism research of negative pressure produced for jet device[J]. Coal Mine Machinery, 2012, 33(7): 77-79.
[16] 罗惕乾. 流体力学[M]. 4版. 北京: 机械工业出版社, 2017.
LUO Tiqian. Fluid Mechanics[M]. Beijing: China Machine Press, 2017.
[17] 田莉, 李家春, 赵先锋, 等. 水肥一体化施肥机变量吸肥系统的设计与试验[J]. 农机化研究, 2019, 41(10): 74-79.
TIAN Li, LI Jiachun, ZHAO Xianfeng, et al. Design and experiment of fertigation system variables of water and fertilizer integrated fertilizer applicator[J]. Journal of Agricultural Mechanization Research, 2019, 41(10): 74-79.
[18] 李家春, 田莉, 周茂茜, 等. 水肥一体化施肥机关键部件的设计与试验[J]. 中国农村水利水电, 2018(10): 148-152.
LI Jiachun, TIAN Li, ZHOU Maoqian, et al. The design and test of key parts of water fertilizer integrated fertilizer applicator[J]. China Rural Water and Hydropower, 2018(10): 148-152.
[19] 王永涛, 刘坚, 李家春, 等. 并联四文丘里管施肥器“旁路吸肥”模式性能分析[J]. 排灌机械工程学报, 2021, 39(9): 959-965.
WANG Yongtao, LIU Jian, LI Jiachun, et al. Performance analysis of “bypass suction fertilizer” mode of parallel four-Venturi tube fertilizer applicator[J]. Journal of Drainage and Irrigation Machinery Engineering, 2021, 39(9): 959-965.
[20] 李彦彬, 马嘉彤, 李道西, 等. 改进粒子群算法在农业种植结构优化中的应用[J]. 灌溉排水学报, 2022, 41(1): 62-71.
LI Yanbin, MA Jiatong, LI Daoxi, et al. An improved particle swarming optimization method to optimize cropping systems[J]. Journal of Irrigation and Drainage, 2022, 41(1): 62-71.
[21] 於沈刚, 马明舟, 岳雪峰, 等. 模糊PID智能灌溉控制器的设计及MATLAB仿真[J]. 节水灌溉, 2018(5): 86-89.
YU Shengang, MA Mingzhou, YUE Xuefeng, et al. Design and MATLAB simulation of intelligent irrigation controller based on fuzzy PID algorithm[J]. Water Saving Irrigation, 2018(5): 86-89.
[22] 刘洋. 基于智能PID的小功率柴油发电机调速器的研制[D]. 成都: 电子科技大学, 2014.
LIU Yang. Research of low-power diesel generator speed governor based on intelligent PID[D]. Chengdu: University of Electronic Science and Technology of China, 2014.
[23] 刘金琨. 先进PID控制MATLAB仿真[M]. 4版. 北京: 电子工业出版社, 2016: 123-128.
LIU Jinkun. Advanced PID Control MATLAB Simulation[M]. 4th Edition. Beijing: Publishing House of Electronics industry, 2016: 123-128.
Using the Smith PSO-Fuzzy PID Model to Control Electrical Conductivity of Nutrient Solution of Precision Fertilization
WANG Yongtao1,2, LIU Jian1*, LI Jiachun3, CHEN Bo3, LI Qing3
(1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China; 2. Guizhou Institute of Water Resources Science, Guiyang 550002, China;3. School of Mechanical Engineering, Guizhou University, Guiyang 550025, China)
【Background and objective】Precision irrigation and fertilization not only improve crop yield and quality but also reduce the environmental footprint of agriculture. How to control precise irrigation and fertilization at large scales is a key to achieving this goal. The objective of this paper is to propose such a methodology. 【Method】The method is based on a multi-channel water and fertilizer integration device. It consists of seven parts: an industrial aluminum profile frame, a main pipeline system, a fertilizer suction system, a fertilizer mixing system, a detection system, a control system, and a fertilization system. Based on the PSO optimized Fuzzy PID, a Smith control system (Smith PSO-Fuzzy PID) for water and fertilizer application is constructed. Takingof the nutrient solution being 2 mS/cm as the control target, the proposed method is compared with the traditional PID, and the fuzzy PID (Fuzzy PID).【Result】The steady-state time and the overshoot calculated by the proposed method are 47 s and 4.83%, respectively; theof the nutrient solution calculated by the proposed method is in the range of 1.987~2.080 mS/cm, very close to the targeted value. 【Conclusion】Compared with traditional PID and Fuzzy PID, the proposed method for controlling water and fertilizer application has the advantages of fast response and high precision.
Smith; PSO; Fuzzy PID control; water and fertilizer integration
王永涛, 刘坚, 李家春, 等. 基于Smith PSO-Fuzzy PID的营养液值调控模型研究[J]. 灌溉排水学报, 2022, 41(11): 37-44.
WANG Yongtao, LIU Jian, LI Jiachun, et al. Using the Smith PSO-Fuzzy PID Model to Control Electrical Conductivity of Nutrient Solution of Precision Fertilization[J]. Journal of Irrigation and Drainage, 2022, 41(11): 37-44.
1672 - 3317(2022)11 - 0037 - 08
S275
A
10.13522/j.cnki.ggps.2022059
2022-01-27
贵州省科技厅项目(黔科合服企[2021]4号);贵州省科技厅项目(黔科合支撑[2021]一般469);国家水利技术示范项目(SF-201913)
王永涛(1986-),男。博士研究生,主要从事智能检测与识别技术研究。E-mail: 409011805@qq.com
刘坚(1975-),男。教授,博士生导师,主要从事智能制造、机器视觉、智能运维等研究。E-mail: liujian0108@vip.163.com
责任编辑:赵宇龙
