基于机器学习的韶关地区短期日平均气温研究

罗 威，罗烨泓，王 威

(1.兴宁市气象局,广东兴宁 514500；2.韶关市气象局,广东韶关 512028；3.深圳市气象局，广东深圳 518000)

自工业革命以来，人类活动所导致的大气二氧化碳排放量剧增，更多的热量被截留在大气层内，致使地球气温增高。受此影响，全球平均表面温度自工业革命以来表现出显著的上升趋势。全球变暖会引起冰雪融化、冻土消融、海平面上升、极端天气频发等，其严重威胁了全球自然生态系统，乃至人类的生存[1-6]。为此，开展针对全球气温的精细化预报研究具有重要现实意义。

近年来，监督类机器学习(树模型、支持向量机、神经网络等)和深度学习算法等各类机器学习算法已在气象短临[1]、中短期[2]乃至长期预报[3]等领域发挥了积极的重要作用，其在相关领域中的表现要显著优于统计和主观经验等传统方法。相较于其他方法而言，监督类机器学习算法能够更有效综合应用来自观测、数值模式等多源数据，据此可更有效地提取大气的非线性演化特征，进而提升数值模式的天气预报效果。然而，受地形、模式参数化方案等不确定性因素的共同影响，目前数值预报模式对气温的预报尚存在一定的偏差，尤其对于中小城市、偏远以及具有复杂地形的地区而言，预报方法通常仅依赖于数值模式，且缺乏有效的补充与优化方法。韶关地区地处南岭山脉南麓，属于亚热带季风气候区，夏无酷暑，冬无严寒，雨量充沛，日照温和，气候条件优越，生态与旅游资源丰富，并且是广东省重要的粮食蔬菜供应地、农业大市。因此，针对韶关地区等中小城市气温预报业务算法的开发对推动气象业务的精细化预报具有重要意义。为此，仅利用1965—2017年韶关地区8个站点的日平均气温观测资料，构建了基于历史数据驱动与机器学习方法的短期气温预报模型，以期为中小城市乃至偏远地区的气温业务预报的改进提供参考，为当地生态环境的改善、社会经济的发展提供科学决策依据。

1 资料和方法

1.1 资料介绍

基于1965—2017年韶关地区8个台站(南雄、曲江、乐昌、仁化、乳源、始兴、翁源和新丰)的日平均气温，求取上述8个站点日平均气温的平均值。台站的基本信息见表1。

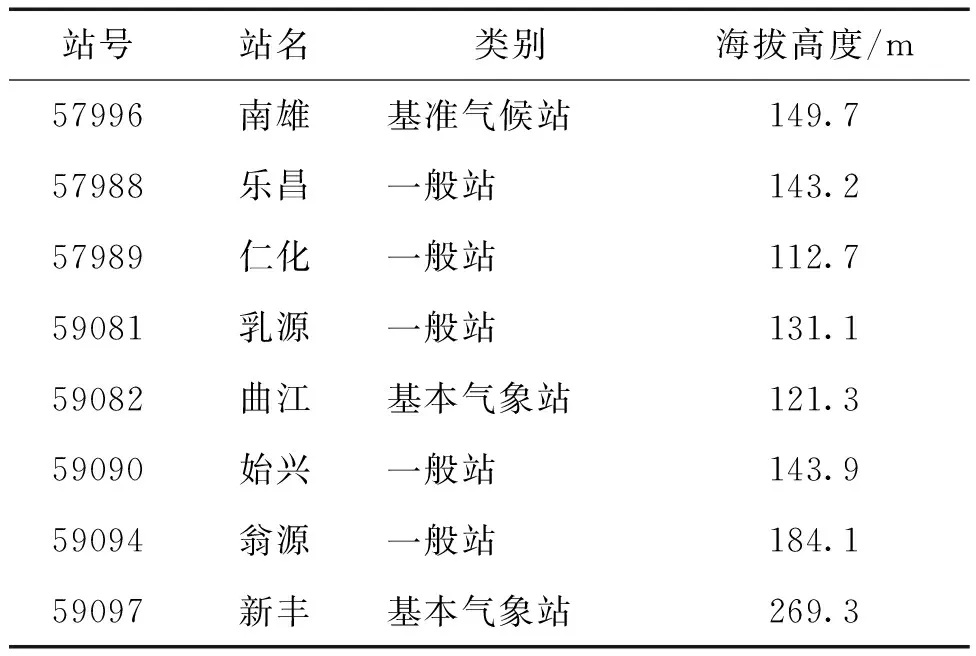
表1 韶关地区各个台站基本信息

1.2 方法介绍

本文用于短期气温预报的算法分别有传统回归方法——逐步多元线性回归法和机器学习方法——LightGBM(light gradient boosting machine)和BP-NN(back propagation neural network)。短期日平均气温预报的流程主要可概括如下：(1)将连续nd的日平均气温(T1,T2, ……,Tn)作为自变量，将第n+1，n+2，n+3天所分别对应的日平均气温Tn+1,Tn+2,Tn+3作为因变量来构建预报Tn+1,Tn+2,Tn+3的模型。(2)n是决定Tn+1，Tn+2，Tn+3预报精度的重要参数，因此在1～365 d的范围内对n进行遍历，最终确定了n=7时可使T8，T9，T10的预报效果达到最优。即将过去连续7 d的日平均气温(T1,T2, ……,T7)作为自变量，以未来3 d日平均气温(T8，T9，T10)作为因变量，来构建相应的日平均气温预报模型。

1.2.1 逐步多元线性回归 逐步多元线性回归[4]是基于最优的自变量来构建回归模型，其较好地解决了传统多元线性回归法中所存在的共线性问题[5]，从而有利于回归模型获得更加精确的计算效果。目前，多元逐步线性回归法已被广泛应用于气象领域，其详细流程可详见文献[4]。

1.2.2 LightGBM(light gradient boosting machine)算法 LightGBM[6]是微软在2017年提出的基于GBDT的算法。相较于传统树模型而言，LightGBM预报精度更高、模型泛化性更强、计算效率更快，适用于大规模数据集的并行计算。LightGBM算法的原理参照文献[6]。

1.2.3 BP-NN(back propagation neural network)算法 BP-NN算法的原理参照文献[7]。为避免权重参数过多而引起过拟合，本文的BP-NN仅5层，由1层输入层、3层隐藏层、1层输出层组成，其中隐藏层的特征维度为100。为了增强BP-NN的训练/预报效果，采用如下优化机制。(1)Kaiming初始化方案[8]；(2)Relu激活层[9]；(3)L2正则化方案[10]，权重衰减系数为0.000 1；(4)Adam优化算法；(5)余弦退火的学习率衰减策略：学习率随训练迭代次数的增大而呈现余弦的周期形态变化，变化的周期为100次迭代，学习率最大值为0.001，最小值为0.000 01；(6)均方误差(mean square error, MSE)的损失函数；(7)自变量与因变量均采用最大最小值归一化。

2 结果与分析

2.1 Tn+1, Tn+2, Tn+3与T1～n之间的相关性

表2为Tn+1,Tn+2,Tn+3与T1～n(n=7)之间的相关性，从表2可见，随着自变量与因变量之间时间间隔的增大，其对应的相关性逐渐降低，但总体仍十分显著。因此，其显著的相关性为以历史日平均气温作为自变量来预报未来短期内的日平均气温奠定了基础。

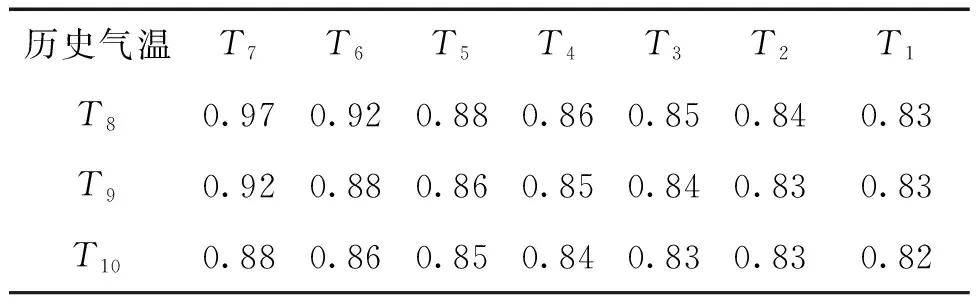
表2 未来日平均气温与历史日平均气温之间的相关性

2.2 三种短期日平均气温预报模型的构建

取1965—2014年的日平均气温作为逐步多元线性回归法建模数据集，并作为LightGBM与BP-NN模型的训练集，2015—2016年的作为两种机器学习模型的验证集，2017年的则作为上述三种模型适用性分析的测试集。其中训练集用于训练构建上述三种模型，验证集用于监控机器学习模型的训练情况。当LightGBM与BP-NN超过100次的训练迭代而验证集误差不再下降时则停止训练，以防过拟合。两种模型均训练迭代1 000次，训练结束后保存验证集误差最低的模型。

2.2.1 基于逐步多元线性回归的模型 日平均气温之间显著的相关性(表2)极易带来共线性问题，进而导致普通线性回归方法存在计算的不稳定性问题。为此,本文采用了逐步线性回归方法来构建短期日平均气温预报模型。

通常情况下，可认为方差膨胀因子≤10时不存在明显的共线性[5]。据此，预报未来1～3 d短期日平均气温的多元逐步线性回归方程如下。

T8=0.656+0.967T7，

(1)

T9=1.024+0.757T7+0.192T2，

(2)

T10=1.551+0.645T7+0.278T3。

(3)

通过逐步多元线性回归分析发现，在满足方差膨胀因子≤10的条件下，T8的自变量因子仅为T7，也表明T1～6与T7之间存在显著的共线性；T9的自变量因子为T7和T2，其对应的方差膨胀因子均为3.545；T10的自变量因子则为T7和T3，其对应的方差膨胀因子均为3.876。可见时间间隔更久远的气温反而可能是未来气温的重要影响因子。建模数据集的拟合结果表明，式(1)、式(2)和式(3)的计算值与实测值之间的拟合相关系数分别为0.97、0.93、0.90，拟合平均绝对误差(mean absolute error, MAE)分别为1.32、2.04、2.42 ℃。

2.2.2 基于LightGBM的模型 利用LightGBM算法计算的训练集T8,T9,T10与实测值之间的拟合R分别为0.98、0.95、0.93，MAE则分别为1.09、1.68、2.00 ℃。

2.2.3 基于BP-NN的模型 利用BP-NN算法计算的训练集T8,T9,T10与实测值之间的拟合R分别为0.97、0.93、0.91，MAE分别为1.22、1.94、2.30 ℃。

2.3 三种模型的适用性

从2.2节针对三种短期日平均气温预报模型的建模结果可知，LightGBM的预报效果最优，BP-NN次之，逐步多元线性回归最差。将上述三种算法应用于2017年的测试集，就各自在短期日平均气温预报中的适用性展开系统分析。

首先分别绘制了上述三种算法日平均气温预报值与实测值之间的时间序列图(图1)。从图1可知，针对T8的预报效果而言，逐步多元线性回归、LightGBM、BP-NN的预报值与实测值之间的R分别为0.97、0.98、0.97，MAE分别为1.25、1.17、1.22 ℃；T9的R分别为0.93、0.94、0.93，MAE则分别为1.88、1.76、1.87 ℃；T10的R分别为0.89、0.93、0.91，MAE则分别为2.22、1.96、2.12 ℃。可见三种算法在测试集上的预报效果与训练集表现基本一致，具有优良的泛化性，其中LightGBM的预报效果最优，BP-NN次之，逐步多元线性回归最差。

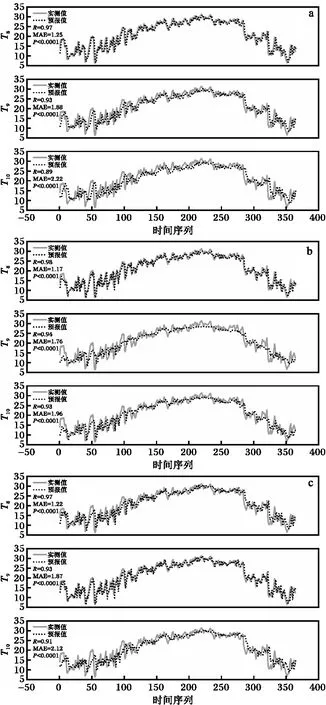
图1 三种模型日平均气温预报值与实测值的时间序列(a 逐步多元线性回归；b LightGBM；c BP-NN)

在实际的气温预报业务中，当气温的预报误差小于2 ℃时可认为预报正确。为此，分别统计了三种算法日平均气温预报值的准确率及其与实测值之间的MAE(表3)。从表3可知，就T8的预报结果而言，三者预报准确率可分别高达83.29%、84.38%、82.73%，MAE为1.25、1.17、2.22 ℃；就T9而言，三种模型的差异性明显体现，三者预报准确率分别为64.38%、69.86%、63.56%，MAE为1.88、1.76、1.87 ℃；就T10而言，三者预报准确率分别为56.44%、61.37%、59.18%，MAE为2.22、1.96、2.12 ℃。

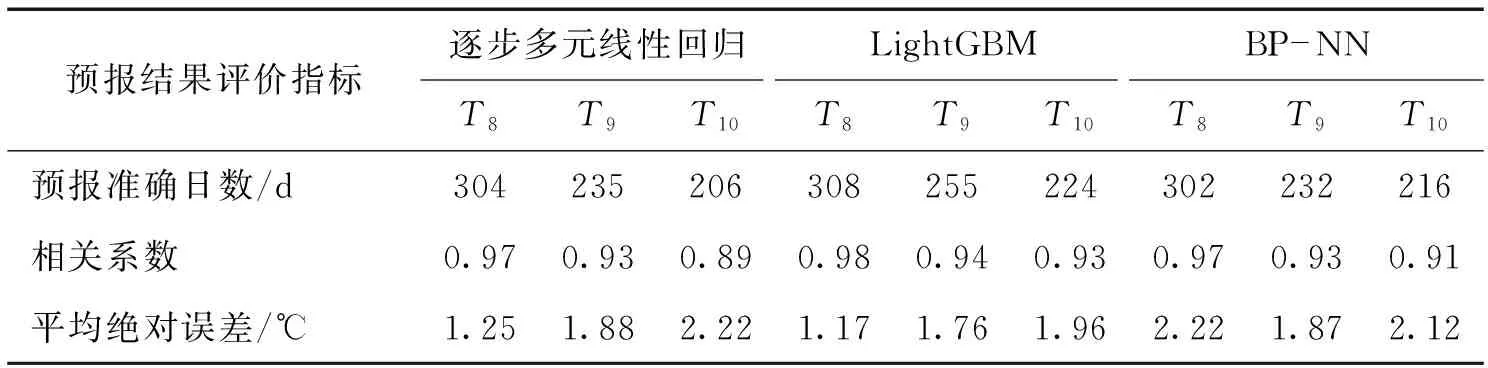
表3 三种模型日平均气温的预报结果评价指标

综上可见，相较于逐步多元线性回归法和BP-NN而言，LightGBM不仅在相关系数以及精确度上更占优势，并且具有更高的预报正确率。尤其随着预报时效的增大，LightGBM具有更优的预报效果，而BP-NN与逐步线性回归法的预报效果则均急剧下降，说明LightGBM具有最优的预报稳定性。推测样本数量较少可能是三种模型预报效果存在显著差异的最主要原因。传统的机器学习模型，如LightGBM、Xgboost、Catboost等更适用于百万级以下的样本量。

明确模型预报误差的时间分布情况对于提高气温的预报精度具有重要意义。为此，绘制了三种模型日平均气温预报值与实测值之间绝对误差(absolute error, AE)的时间序列图(图2)。从图2可见，相同预报时效，三种模型所表现的AE波动形态基本一致。但总体而言，LightGBM的AE及其波动幅度最小，其预报未来3 d气温绝对误差的标准差(standard deviation，STD)分别为1.09、1.53、1.65 ℃；BP-NN次之，STD分别为1.15、1.66、1.97 ℃；逐步线性回归最大，STD则分别为1.23、1.73、2.00 ℃。此外，逐步多元线性回归以及BP-NN的AE及其波动幅度均随着预报时效的增大而显著增大，但LightGBM则相对最为稳定。另外从图2不难看出，三种模型AE的大值区基本位于0～100日以及240～365日，即处于冬春季以及秋冬季。结合图1可推测，该时期气温较大的波动性会加大机器学习模型的训练难度，进而导致AE的总体偏大。

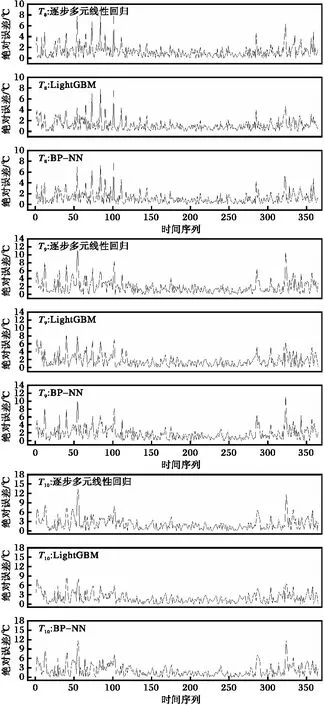
图2 三种模型针对未来1～3 d日平均气温预报的绝对误差(AE)时间序列

综合上述分析可知，LightGBM和BP-NN机器学习方法在预报准确性,拟合效果(R)以及稳定性(AE)方面均要优于逐步多元线性回归法。

3 结论和讨论

(1)通过对过去1～365 d的日平均气温进行遍历测试，确定将过去连续7 d的日平均气温分别作为逐步多元线性回归、LightGBM以及BP-NN算法的自变量可最准确地预报出未来1～3 d的日平均气温，据此构建了短期气温预报模型。该最优自变量的确定方法是以结果为导向，其中所表征的科学背景仍有待进一步探索。

(2)从预报准确率(绝对误差小于2 ℃的天数占比)，相关系数和绝对误差来看，三种模型均能较准确地预报出未来1～3 d的短期日平均气温，其中LightGBM最优，BP-NN次之，逐步多元线性回归最差。以LightGBM为代表的传统机器学习模型适用于非图像领域百万级左右的数据集，而对于雷达回波外推以及空间降尺度等图像领域， 则要以神经网络为代表的深度学习方法更为适用。

(3)数据的质量决定了预报效果的上限，而模型只是协助逼近该上限。因此，增加更多的观测与模式预报资料，通过采用特征工程等方法，将有助于进一步提升算法的预报性能。