多重放大的医学图像超分辨率重建
2022-12-06章伟帆曾庆鹏
章伟帆,曾庆鹏
南昌大学 信息工程学院,南昌 330031
随着CT、磁共振等医疗影像技术的广泛应用,医学图像已成为临床诊断过程中的重要参考信息。医学图像的质量会对医生的临床判断产生重要的影响,清晰且纹理细节丰富的医学图像可以提供更加全面的病理信息[1]。高分辨率的医学成像设备往往造价高昂,通过增加扫描次数或扫描时间取得高分辨率医学图像的方式,易出现过量辐射或运动伪影的情况[2]。单幅图像超分辨率(single image super-resolution,SISR)是指通过一幅低分辨率(low-resolution,LR)图像,生成高分辨率(highresolution,HR)图像的过程[3],其被广泛应用于安防监控、医学图像和卫星遥感等领域中[4]。利用超分辨率重建的方法获取高质量的医学图像,成本更低,安全风险更小。
超分辨率重建的方法大致可以被分为三类[5]:基于插值的方法,基于重构的方法,以及基于学习的方法。插值法实现起来更简单,但重建得到的图像易出现混叠与模糊的现象[6]。重构法通常需要明确的先验信息对结果进行约束,相比插值法重建效果更好,但往往难以确定求解模型,在较大的放大因子下易出现先验信息不足的问题[7]。浅层学习法一般需手动地选择图像特征和参数,并进行手工的调整,建立LR图像和HR图像之间的映射关系[8],对人员专业性要求较高。
深度学习的方法并不显式地学习LR图像与HR图像之间的映射,而是通过训练网络模型取得一组权值,隐式完成二者之间的映射。Dong等人[9]首先将深度学习的方法引入SISR问题,提出基于卷积神经网络的图像超分辨率网络模型SRCNN。与传统方法相比,重建效果得到明显提高。但对LR图像插值放大至HR大小后输入网络模型,增加了计算负载。Dong等人[10]在SRCNN上进行改进,提出基于反卷积的快速图像超分辨率网络模型FSRCNN。可直接输入LR图像进行处理,在网络模型的末端利用反卷积的方法,将特征图放大至HR大小。显著地提高了图像的重建速度,但易出现棋盘伪影等现象。Shi等人[11]引入亚像素的概念,提出基于亚像素卷积的超分辨率重建网络模型ESPCN。在末端利用亚像素卷积对特征图进行像素重排。反卷积法与亚像素法也被应用到后续众多基于深度学习的超分辨率重建网络模型中。
Kim等人[12]将残差跳跃连接结构引入超分辨率重建任务,提出了基于深度卷积神经网络的超分辨率重建网络模型VDSR。通过残差连接能够建立更深的网络结构,增强网络模型的特征提取能力。Tong等人[13]将密集连接结构引入超分辨率重建任务,提出基于密集跳跃连接的超分辨率重建网络模型SRDenseNet。在网络层之间建立更为激进的跳跃连接结构,每一层的输入都来自于之前所有层的融合,实现浅层特征的复用。Zhang等人[14]结合残差连接与密集连接,提出基于密集残差网络结构的图像复原网络模型RDN。实现特征与梯度的良好传递,取得了更好的重建效果。
当前大多数基于深度学习的超分辨率重建网络模型都只针对彩色的自然图像,面向医学图像重建任务的较少。医学图像往往纹理细节更加复杂,对图像结构的准确还原有更高的要求。此外,大多数基于深度学习的方法都需要为每个放大因子单独训练一个模型,且局限于整数放大因子,限制了重建模型的实际应用。
为此,本文提出一种支持多重放大的医学图像超分辨率重建网络模型(multi-scale medical image superresolution used 2-RDB,M2SR)。改进密集残差结构的跳跃连接方式,逆序方式建立更为稀疏的层间连接,将连接复杂度由指数级降至对数级,改善网络模型不平衡的问题。采用元信息直接嵌入模式对特征图重建结构进行改进,跨任务地学习不同放大因子间的通用知识,并动态地生成权值。所提的M2SR网络模型同时考虑像素坐标信息与放大因子信息,较好地实现了小数与整数放大因子重建任务的整合。
1 相关工作
1.1 密集残差块
对于卷积神经网络而言,往往越深的网络,训练得到的结果会越好。但是随着网络的加深,容易出现梯度消失或梯度爆炸的现象。He等人[15]提出残差学习的思想,通过增加跳跃连接,直接将梯度由网络的浅层传递至深层部分,较好地解决了深层网络难以训练的问题。Huang等人[16]进一步提出了密集连接结构。在密集块中,每一个卷积层的输入都是之前所有层的输出。密集残差网络结构则融合了密集连接和残差学习的思想,基本组成单位为密集残差块(residual dense block,RDB),其主要结构如图1所示。
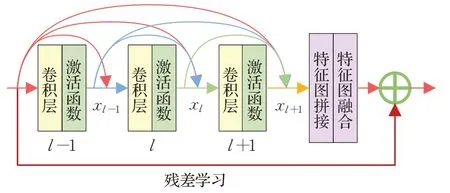
图1 密集残差块结构Fig.1 Structure of residual dense block
通常的网络传播方式中,第l+1层的输入只来源于第l层的输出xl。在残差密集块中,第l+1层的输入则来源于之前的所有层,如公式(1)所示:
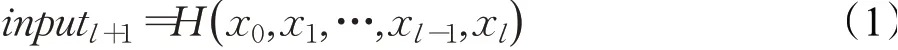
其中,函数H()·表示各层输出的特征图在通道方向上的拼接融合。通过Padding操作,保持每个卷积层输出的特征图大小一致。在密集残差块中,总的跳跃连接数量如公式(2)所示:

其中,Nskip表示总的跳跃连接数量,NL表示密集残差块内卷积层数量。总的连接数量呈指数级O(n2)增长。特征图融合层利用1×1卷积,对拼接后的特征图进行降维融合,以匹配下一个密集残差块的输入。
1.2 元学习
元学习也可以被称为学会学习。一般的机器学习策略往往是对训练数据的学习,元学习则上升为对任务的学习[17]。元学习往往将一组相近的任务看作某个复杂任务的简单子任务,通过跨任务的比较学习,获得各个简单子任务间可迁移的通用知识[18]。元学习被广泛应用于零样本学习、少样本学习与迁移学习等领域[19]。最简单直接的元学习策略则是元信息动态嵌入模型的模式。通常元学习策略通过跨任务学习超参后再取得一组权重,元信息动态嵌入的模式直接由训练任务取得权重,越过超参赋值的过程。在图像处理领域中,往往是动态地更新不同子任务的权重。在分类任务中,Cai等人[20]利用元学习策略,将分类模型迁移至新的小样本分类任务,使网络模型获得对新类别的分类能力。在目标检测任务中,Yang等人[21]结合元学习策略,动态地生成检测锚点与边界,不再需要进行预定义的操作。本文利用元学习策略学习不同放大因子重建任务间的通用知识,嵌入一个小型的神经网络更新特征图放大重建部分的权重,完成多重放大因子的医学图像超分辨率重建任务。
2 M2SR网络模型
2.1 改进连接的2-RDB结构
本文对原密集残差结构中的跳跃连接进行了改进,提出2-RDB结构,并作为M2SR网络模型的一部分。其结构如图2所示。

图2 改进连接的2-RDB结构Fig.2 Structure of 2-RDB modified skip
在2-RDB结构中仍保留残差跳跃连接,对于密集跳跃连接则有两种组织方式:双层跳跃与多层跳跃。双层跳跃以2个卷积层为一组添加跳跃连接,多层跳跃以2倍增长的方式,逆序地确定跳跃连接的位置。
在图2中对2-RDB中的卷积层进行编号,上方的为正序编号,下方的为逆序编号。多层跳跃连接的特征图拼接融合如公式(3)所示:
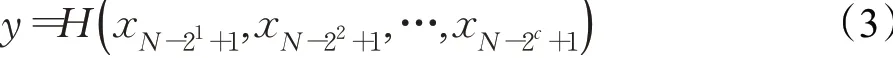
其中,函数H(·)表示对特征图拼接融合,xi表示第i层的输入,N表示2-RDB中卷积层的数量,c为正整数,满足2c≤N。公式(3)中为正序编号表示,若由逆序表示,则需传递的是第-2n卷积层的输入。以图2中由8个卷积层组成的2-RDB为例,需连接第-2、-4、-8个卷积层的输入,即正序编号的第1、5、7个卷积层的输入。
在改进连接的2-RDB结构中,密集跳跃连接的数量如公式(4)所示:
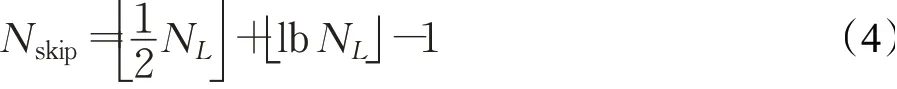
改进后的结构中,连接数量以对数级O(lbn)增长。与公式(2)相比,连接复杂度由指数级降至对数级。避免了网络层数增长时,连接数量爆炸增长的问题。
此外,2-RDB中的多层跳跃使连接操作集中于网络模型的末端,增强对深层特征的提取能力,能够更好地还原医学图像的细微纹理信息。原密集残差结构中,来自浅层的特征图会被反复传递,在网络的末端,新增的存储状态多数被用于保存浅层特征。逆序编号的多层跳跃方式改善了原结构中,浅层特征占比过高的问题。
多层跳跃方式下,网络模型前端的连接较为稀疏。为此,以两个卷积层为一组添加双层跳跃连接,以维持浅层特征的良好传递能力,改善原网络模型结构不平衡的问题。
2.2 M2SR网络模型的整体结构
M2SR网络模型以2-RDB结构为主要组件,并采用元信息动态嵌入的模式,实现多重放大的医学图像超分辨率重建任务。其整体结构如图3所示。
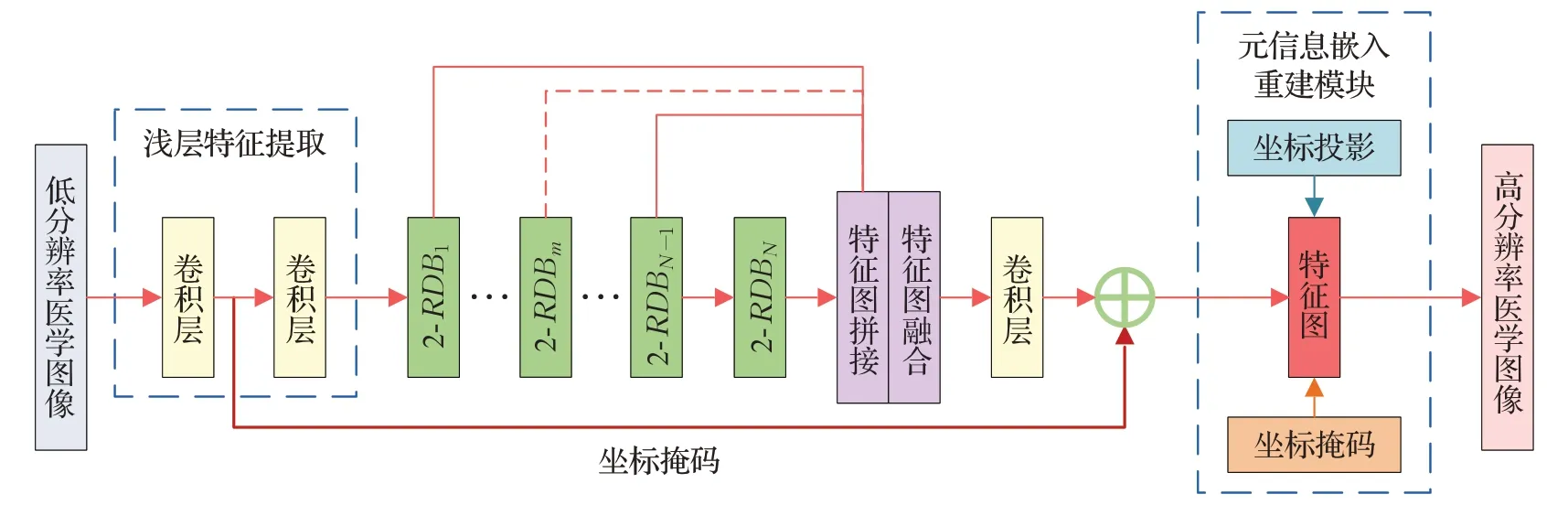
图3 M2SR网络模型的整体结构Fig.3 Framework of M2SR network
本文提出的M2SR网络模型仍保持原密集残差网络模型的基本组成方式,特征提取部分则由若干个2-RDB依次连接而成。不再将所有的2-RDB块间的输出进行传递,而是有间隔地输出至网络末端进行拼接融合操作,跳跃连接总数降低至N/2,如公式(5)所示:
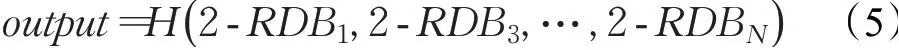
特征图的放大重建部分采样元信息动态嵌入的模式,通过坐标投影矩阵与坐标掩码矩阵对特征图进行重构,以还原高分辨率的医学图像。
此外,在M2SR网络模型中,一律不包含池化与批归一化操作。池化操作容易引起模糊效应,会对医学图像的纹理信息造成破坏。批归一化操作主要用于突出相对差异,而低分辨率与高分辨率的医学图像之间高度相似,但绝对差异很大,批归一化操作可能降低重建图像的质量。
基于元学习的重建结构将医学图像的重建任务整体地看作为一个复杂任务,将不同放大因子的重建任务看作该任务的简单子任务。利用元信息直接嵌入的特征图重建模块与向量转换对齐操作,将孤立的不同放大因子医学图像重建任务,转化为对各个简单子任务间通用知识的学习,实现多重放大因子的重建任务。
2.3 元信息嵌入重建模块
一般的重建模型中,在特征图的放大重建阶段是为每个放大因子学习一组固定的权重。在基于元学习的M2SR结构中,将一个小型神经网络直接嵌入特征图重建模块,为不同的放大因子动态生成一组权重。将对数据的学习,转换为对任务的学习。其结构如图4所示。

图4 元信息嵌入结构Fig.4 Structure of meta-information embedding
元信息嵌入结构共有三个输入,特征图F、坐标投影矩阵Ep,以及坐标掩码矩阵Em。坐标投影矩阵Ep由三个矩阵拼接而成,分别保存横、纵坐标信息与放大因子信息。对于HR医学图像上的点P(I,J),其在LR医学图像上有对应投影点p(i,j),当放大因子r为整数时,有公式(6);当放大因子r为小数时,有公式(7):

同时考虑小数与整数放大因子的重建任务,综合公式(6)与公式(7),并考虑放大因子信息,有公式(8):

坐标投影矩阵由X、Y与Z合并构成,以类似图像通道的方向取出一组值,作为权值预测网络的输入,如公式(9)所示:

其中,N(·)表示权值预测网络,由两个全连接层构成,wfc表示其输出,m与n表示坐标投影矩阵上取出点的坐标。通常,使用反卷积或亚像素卷积等方法对特征图进行上采样时,指定某个整数放大因子后,再学习一组相应的固定权重。在M2SR网络模型中,学习嵌入的权值预测网络权重,再根据不同的放大因子动态地生成相应的权重wfc。高分辨率的医学图像重建过程如公式(10)所示:
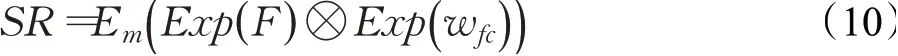
其中,Em(·)表示依据坐标掩码矩阵记录的信息进行矩阵压缩,Exp(·)表示对向量进行复制扩充,选择矩阵乘作为特征映射函数,以联合预测的权重向量与提取的特征图向量。
2.4 维度对齐与坐标掩码
权值向量与特征图向量需提前进行复制扩充,对齐二者维度以满足特征映射函数的运算要求。对于特征图F,假定维度对齐前的输入为(Cfin,h,w),则输出维度为(R,R,k×k×Cfin,h×w)。其中R为放大因子r向上取整,k为滑动窗口的核大小。采用类似卷积的滑动方式复制,以保持向量内部的位置信息不被破坏。对于权值向量wfc,假定维度对齐前的输入为(h×w,wfc),输出的维度为(R×h,R×w,wfc)。方便起见,同样以wfc表示权值向量的维度。此过程中同样需保持向量内部的相对位置稳定。参数k与wfc的选定需满足公式(11):

经过维度对齐后,参数R取代参数r。通过对向量的适当复制扩充,使网络模型能够以相同的方式处理小数放大因子的重建任务。利用坐标掩码还原参数r,取得SR(super-resolution)医学图像。坐标掩码矩阵Em的生成过程如图5所示。
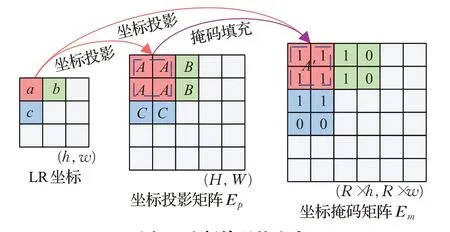
图5 坐标掩码的生成Fig.5 Generative process of coordinate mask
坐标掩码矩阵Em的取得方式同维度对齐过程相适应,以参数R为指导。对于坐标投影矩阵Ep,依据公式(8)确定。在放大因子r为小数的条件下,LR上各点的投影范围并不一定相同。在参数R的条件下,对于LR上的一点a(i,j),其在坐标掩码矩阵Em上有对应的点A"(I",J"),坐标范围满足公式(12):
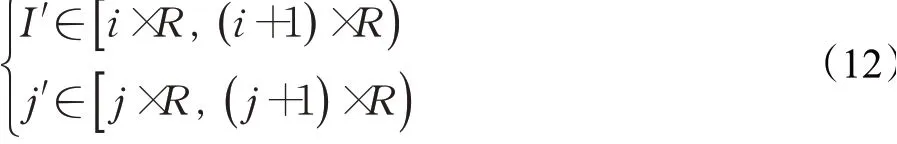
由于矩阵Ep与矩阵Em在不同的参数指导下进行投影,可能出现差余,按位填充坐标掩码矩阵Em以记录。对于特征映射后取得的稀疏像素矩阵,认为其在对应坐标掩码矩阵上置1的点比置0的点更有效,更符合LR至HR的投影范围。将矩阵Em中为0的点作为稀疏标记,对稀疏像素矩阵进行压缩,重建高分辨率医学图像。随着放大因子r的增长,坐标掩码矩阵中稀疏标记减少。当r=R时,矩阵Em与矩阵Ep将完全映射,公式(8)将退化为公式(6)。此时即为整数重建任务,由此实现小数与整数医学图像重建任务的整合。
对于嵌入的权值预测结构,其隐藏层的神经元数量设定,影响元信息嵌入重建结构的表达能力,可参考一般BP网络模型隐藏层参数要求。本文M2SR网络模型中各关键参数设置如表1所示。

表1 网络模型M2SR关键参数Table 1 Key parameters of M2SR network
3 实验结果与分析
3.1 实验数据与训练设置
实验数据来源于美国人类基因组图谱数据库(The Cancer Genome Atlas,TCGA),共包含三类医学图像:宫颈鳞癌和腺癌(cervical squamous cell carcinoma and endocervical adenocarcinoma,CESC)、食管癌(esophageal carcinoma,ESCA),以及肾嫌色细胞癌(kidney chromophobe,KICH)。从各类别样本中挑选200张成像质量较好、纹理细节丰富的医学图像作为训练样本。以不重合的方式,从各类别中额外选择40张作为测试样本,分别标记为测试集a、测试集b与测试集c。在数据预处理时将去除所有标签数据,仅保留图像信息。
退化模型采用常规的双三次插值法方式对HR图像下采样,模拟LR医学图像,取得成对的训练样本组。训练时采用方形的32×32随机裁剪子图,批处理大小设置为16。采用Adam优化器训练网络模型,初始学习率为0.000 1,每100训练代数减半。实验平台操作系统为Ubuntu18.04,硬 件CPU为Intel Xeon E5-2618L v3,GPU为NVIDIA GeForce RTX 2080 Ti,内存32 GB,采用PyTorch1.5版本深度学习框架。
3.2 整数放大因子实验结果
实验结果以峰值信噪比(peak signal to noise ratio,PSNR)与结构相似度(structural similarity index,SSIM)作为评价指标,以典型方法作为比较基线。双三次插值法(bicubic)作为传统方法的典型代表,SRCNN为首次将深度学习引入SISR任务的经典网络模型,VDSR为首次利用残差学习建立的SISR网络模型。特征图上采样重建主要有反卷积与亚像素卷积两类,分别选择典型的反卷积法[10]与亚像素法[11]网络模型作为比较基线。
在不同放大因子下,M2SR网络模型在PSNR与SSIM上的结果如表2所示。实验结果取各测试集上的平均值,最好结果加粗标记。此外,对各测试结果计算相应的标准差σ,以观察实验结果的离散性。
由表2可以看出,基于深度学习的方法都优于传统的双三次插值法Bicubic。SRCNN方法使用前端上采样策略,可能同步放大LR医学图像的噪声,重建表现较差。与反卷积法与亚像素法相比,M2SR网络模型在×2任务中,PSNR指标平均提升1.25 dB与1.05 dB。与同样采用残差结构的VDSR相比,在高倍的×4任务下M2SR网络模型优势相对更为显著,在PSNR与SSIM上提升幅度最大可达1.57 dB与0.042 5。实验结果表明,同各类典型方法相比,M2SR网络模型在整数放大因子医学图像重建任务上保持了良好的重建性能。
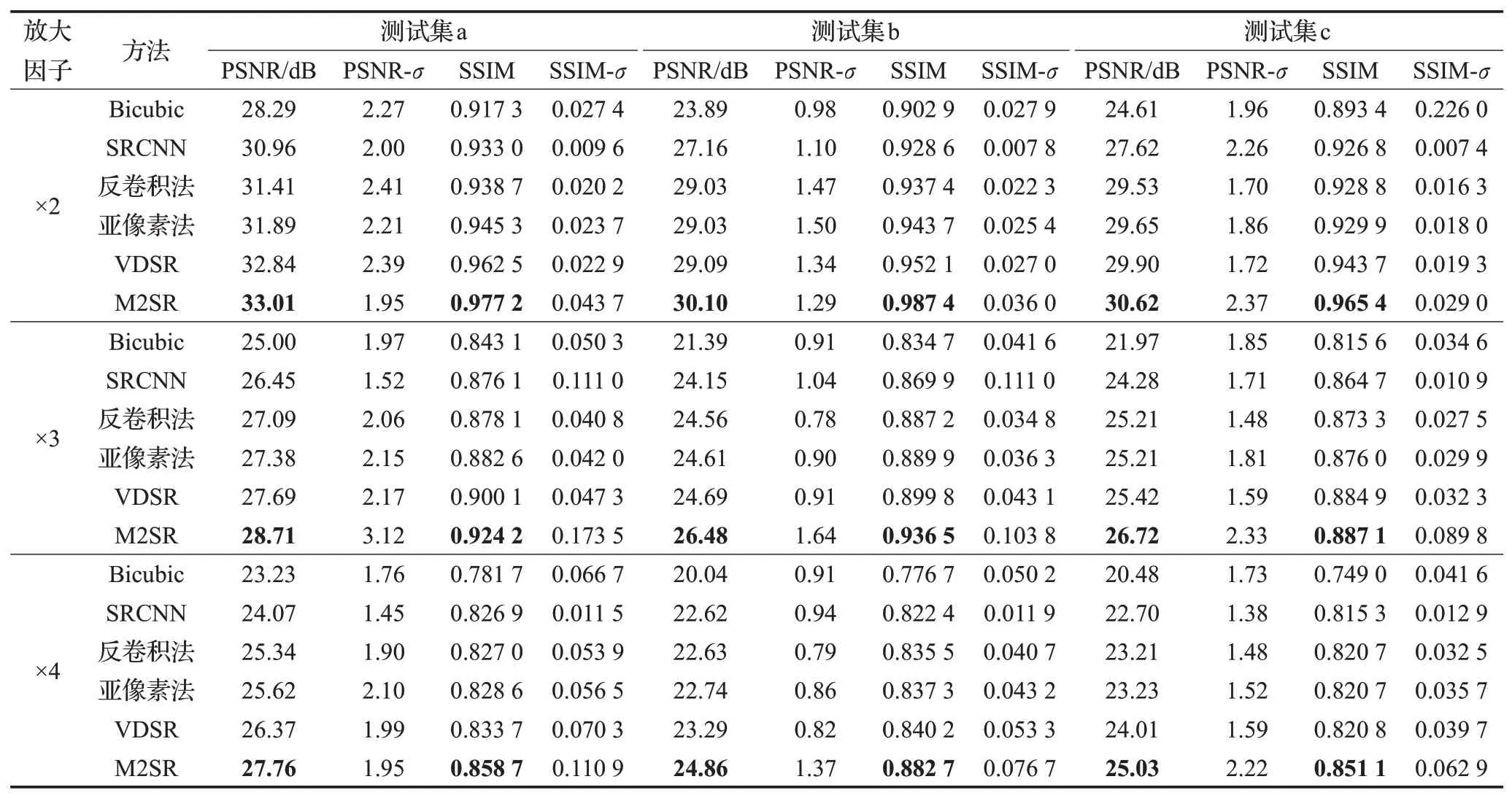
表2 整数放大因子下PSNR与SSIM结果Table 2 Result of PSNR and SSIM for integer scale factors
对于主观重建结果,从测试集中挑选3张成像较为清晰、纹理细节较为丰富的医学图像进行重建。各重建医学图像的主观视觉表现如图6所示。
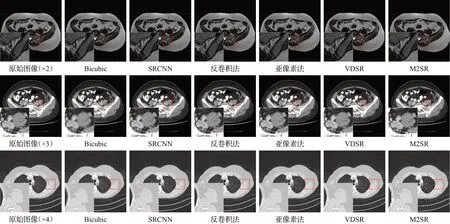
图6 主观重建视觉表现Fig.6 Objective performance of reconstruction in vision
为更直观地展现重建效果,对重建的医学图像进行局部放大。对比各类重建方法的局部放大结果可以看出,传统的双三次插值法Bicubic效果最不理想,重建的医学图像纹理细节部分像素弱化明显。与原始图像的局部放大相比,高频部分丢失严重,整体模糊感相较更强。在较低的×2放大因子任务中,SRCNN与反卷积法和亚像素法相比重建效果相似,但在更大的×4放大因子任务下,SRCNN方法中重建医学图像失真较为严重。对细节进行局部放大,可以看到采用反卷积方法的重建图像出现了较为明显的棋盘伪影现象,整体图像覆盖有一层条状色带。VDSR通过残差跳跃建立了更深的网络结构,重建效果相对更好。但重建的医学图像边缘轮廓过于平滑,低频部分则有较为严重的涂抹感。M2SR网络模型重建效果相对更好,特别在×4放大因子任务下,更好地还原了医学图像的纹理信息。对比局部放大图,M2SR重建图像的边缘信息得到了增强,还原了更多医学图像的高频信息,纹理细节特征丢失较少,重建图像模糊感也更弱。整体上重建图像涂抹感较轻,视觉感受更清晰锐利。
3.3 小数放大因子实验结果
目前主流的基于深度学习的超分辨率重建方法都仅支持整数的放大因子。对于小数的放大因子重建任务,通常的做法是将LR图像经过适当的插入放大后,再作为重建网络的输入。插值输入法以SRCNN网络模型作为基础,对输入的医学图像预先进行适当的上采样,再输入网络模型中重建取得SR医学图像,以模拟小数放大因子任务的重建效果。传统的双三次插值法Bicubic可直接支持小数放大因子任务。
此外,为更加全面地比较M2SR网络模型在小数放大因子任务下的重建效果,设计一个简单的基准实验模型M2SRbase,其结构设计如图7所示。
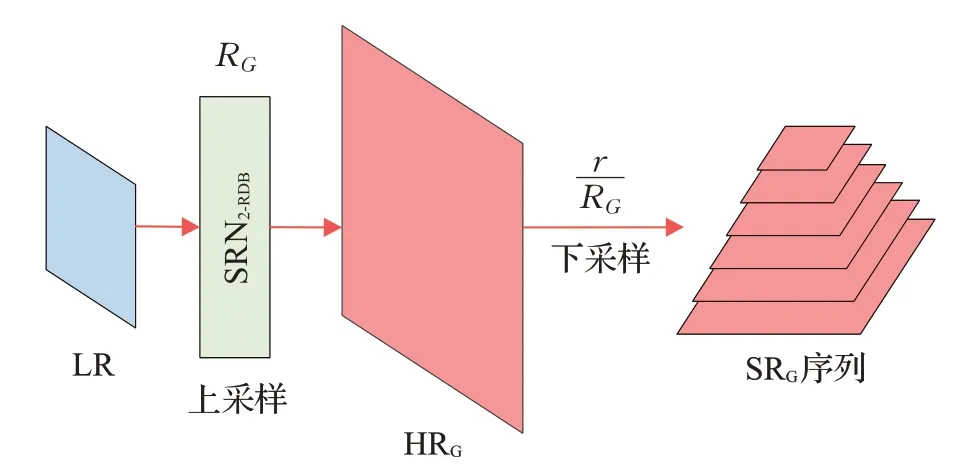
图7 基准实验模型M2SRbase结构设计Fig.7 Design of baseline model M2SRbase
基准实验模型M2SRbase的结构设计以M2SR网络模型为基础。图7中SRN2-RDB网络模型同样地以2-RDB块作为特征提取部分的基本组成结构,特征图重建模块则不采用M2SR网络模型中的元学习结构。对于放大因子为r的医学图像重建任务,首先利用SRN2-RDB网络模型进行上采样重建,再对生成的HRG图像进行适当的下采样获得SRG图像序列,模拟小数的放大因子重建过程。通过设计的基准实验模型,可以比较元信息嵌入重建结构的性能表现。在不同的测试集下,小数放大因子重建任务在PSNR与SSIM上的结果如表3所示,最优的结果加粗表示。
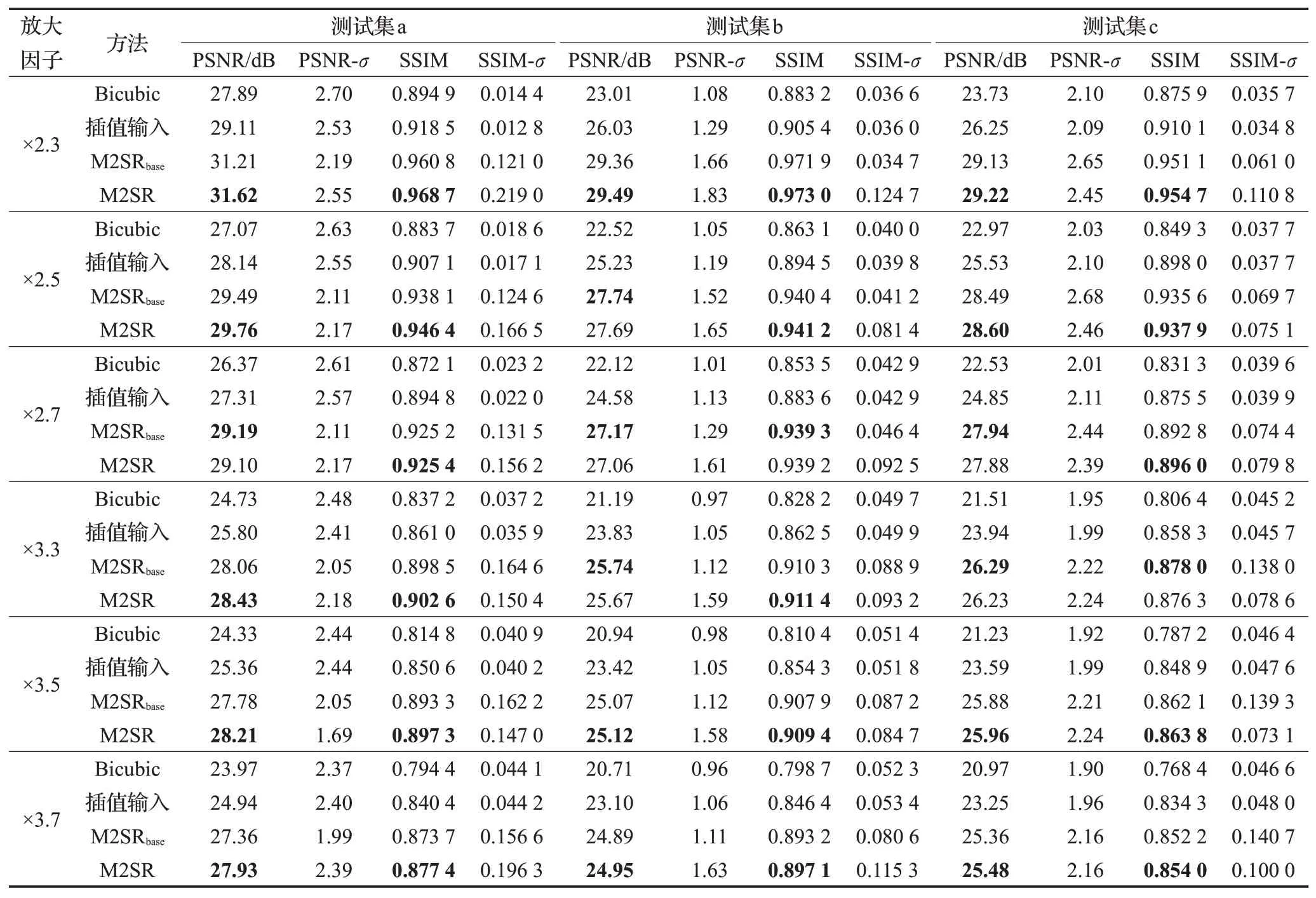
表3 小数放大因子下PSNR与SSIM结果Table 3 Result of PSNR and SSIM for fraction scale factors
同双三次插值法和插值输入法相比,在各类测试集下M2SR性能表现均有较大提升。在测试集a上,M2SR相较于插值输入法PSNR指标最大提升2.99 dB,SSIM提升幅度最大可达0.502 0。插值输入法需对输入图像预先适当上采样以模拟小数放大因子重建任务,可能出现对图像噪声的二次放大。M2SR则可通过单个训练模型直接重建小数放大因子医学图像,并取得了相对较好的性能表现。
同所设计的基准实验模型M2SRbase相比,M2SR网络模型重建效果略有改善。在测试集a上性能表现最好,测试集b上相对略差。M2SR网络模型在实现多重放大因子的医学图像重建任务的情况下,小数放大因子重建任务仍表现出与整数放大因子重建任务相似的性能。元信息直接嵌入重建结构较好地整合了小数与整数放大因子重建任务。
3.4 消融实验
网络模型M2SR主要对超分辨率重建过程中的特征提取与特征图重建两部分进行改进。为比较2-RDB结构与元信息嵌入结构对医学图像重建效果的贡献,设计消融实验。在测试集b与放大因子×4的条件下,消融实验结果如表4所示。
通过适当地设置基准实验模型M2SRbase中的参数,可作为消融实验的一部分。当设置参数RG=4时,有RG=r,基准实验模型M2SRbase将不对模拟的HRG图像下采样,可比较元信息嵌入重建结构对M2SR性能提升的贡献。如表4中所示,元信息嵌入结构与2-RDB结构都对最终重建性能有所提升,其中元信息嵌入方式提升相对较小。在整数放大因子下,坐标投影矩阵Ep中的横纵坐标信息矩阵被置为0,与小数放大因子任务相比缺少坐标信息。
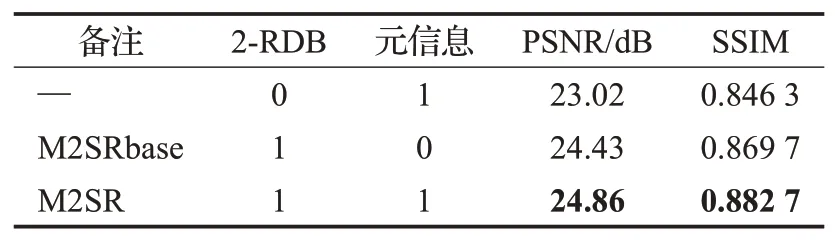
表4 消融实验结果Table 4 Result of ablation experiment
4 结束语
本文针对医学图像纹理丰富的特点,基于密集残差结构分别对特征提取与特征图重建进行优化,提出多重放大的医学图像超分辨率重建网络模型M2SR。改进密集块内跳跃连接的方式,建立更为稀疏的双层跳跃和多层跳跃,并作为特征提取结构的基本组成部分。融合元学习策略,采用元信息直接嵌入模式重新设计特征图重建结构。同时考虑坐标信息与放大因子信息,学习不同放大因子重建任务间的通用知识。M2SR网络模型有效降低跳跃连接复杂度,改善网络结构不平衡的问题,实验结果表明,M2SR网络模型较好地实现了小数与整数放大因子医学图像重建任务的整合。
本文所提的M2SR网络模型可通过单个训练模型实现多重放大因子的重建任务,并且基于软件的重建方式使其可直接整合至现有的医学成像系统。但在特征映射过程中的复制扩充操作,对计算机存储资源要求较高,且只针对二维医学图像。因此,未来的工作将针对于重建过程的高效实现,以及三维医学图像的多重放大重建任务。
