一种平衡衔铁受话器数值仿真分析方法

蒋 钰，陆 晓，温周斌

(1.中国科学院声学研究所东海研究站，上海 201815；2.中国科学院声学研究所，北京 100049；3.中国科学院大学，北京 100190；4.浙江中科电声研发中心，浙江 嘉善 314115)

0 引言

平衡衔铁受话器(Balanced Armature Receiver,BAR)，具有尺寸小、电声转换效率高和灵敏度高等特点[1-2]，已被广泛用于助听设备、入耳式耳机和各种军用头戴式耳机等产品中[3]。近年来，随着消费者对声品质要求提高，平衡衔铁受话器的应用更为广泛。

数值仿真分析是一种通过计算机进行数值计算求解一组满足一定边界条件的微分方程，并得到其近似解的方法[4]，已广泛应用于动圈式扬声器单体及系统的主要特性的仿真分析[5-8]。近10年来，国内外学者围绕平衡衔铁受话器的非线性、声压级和失真等主要特性进行了深入研究。Jensen等基于集总参数模型深入研究了平衡衔铁受话器的非线性和失真等特性[9]。基于集总参数模型的仿真分析方法概念清晰、方法简便，但所得到的仿真结果在中高频段精度不够高[10]。Jensen还采用数值仿真分析方法研究了不同平衡衔铁磁导率对应的平衡衔铁上的磁通密度分布[11]。Hu等创建了平衡衔铁受话器的振动系统与声场的数值仿真分析模型，验证了其所提出的多模态模型的有效性[10]。Ziolkowski等将平衡衔铁受话器磁路简化为2D模型，通过耦合电磁场与结构，得到了平衡衔铁的位移[12]。Xu等提出了平衡衔铁受话器电磁场的瞬态分析和基于模态叠加法的平衡衔铁受话器结构与声场的频域分析相结合的方法，利用前者得到的非线性参数和后者得到的力与声压级的传递函数，再通过数值迭代最终得到平衡衔铁受话器输出的声压级[13-14]。

本文首先介绍平衡衔铁受话器及其集总参数模型，分析指出平衡衔铁运动会对扬声器特性带来重大影响；然后提出一种基于COMSOL Multiphysics数值仿真分析软件的平衡衔铁受话器声压级和阻抗的仿真分析方法。该方法首先对平衡衔铁受话器的磁场特性进行稳态分析，计算得到可随平衡衔铁运动变化的驱动力和反电动势；然后对电磁场、结构和声场耦合模型进行频域分析，最终计算得到平衡衔铁受话器的声压级和阻抗。

1 平衡衔铁受话器及其集总参数模型

图1是一款平衡衔铁受话器的半剖几何模型[1]。由图1可知，平衡衔铁受话器由线圈(Coil)、传动杆(Drive pin)、振膜(Membrane)、永磁体(Magnets)、磁轭(Magnet house)、平衡衔铁(Armature)、前盖(Cover)、外壳(Case)和出声孔(Sound outlet)等组成。平衡衔铁一端被固定在外壳上，另一端悬空。平衡衔铁通过驱动杆与振膜连接。振膜被粘于上盖，其中三边有折环，另外一边是金属。平衡衔铁和振膜的振动都是类似于悬臂梁的振动。振膜和上盖之间的空气域定义为前腔，振膜另一面的空气域为后腔。

图1 平衡衔铁受话器半剖几何模型[1]Fig.1 Section model of BAR[1]

当平衡衔铁受话器音圈中无电流通过时，平衡衔铁在磁场中处于受力平衡状态，因而稳定在两个永磁体中间。当线圈中有电流通过时，在线圈周围除了稳定的磁场之外，还有因电流变化所感应出的扰动磁场。平衡衔铁会被扰动磁场磁化，它的磁化方向也会随着流经线圈中电流方向的改变而改变。因此，平衡衔铁所受到的力将不断变化，这个力会使得平衡衔铁上下往复运动。平衡衔铁往复运动将通过传动杆带动振膜上下振动，而振膜的上下振动又会使得前腔的空气压缩或膨胀，从而产生声波，声波再从出声孔传递出去。

建立平衡衔铁受话器的集总参数模型，可分析得到诸多重要参数，进而还可分析得到这些重要参数对扬声器特性的影响。图2(a)给出了一个平衡衔铁受话器的简化的磁回路。将磁阻、磁场力和磁通量分别等效为电阻Rg、电压源FM和电流Φ，可建立该磁回路的集总参数模型，图2(b)是图2(a)的等效电路图[10]。利用该等效电路图，可以得到平衡衔铁中的磁通量和上下磁隙中的磁通量，进而计算得到线圈上所受到的反电动势和平衡衔铁所受的力。

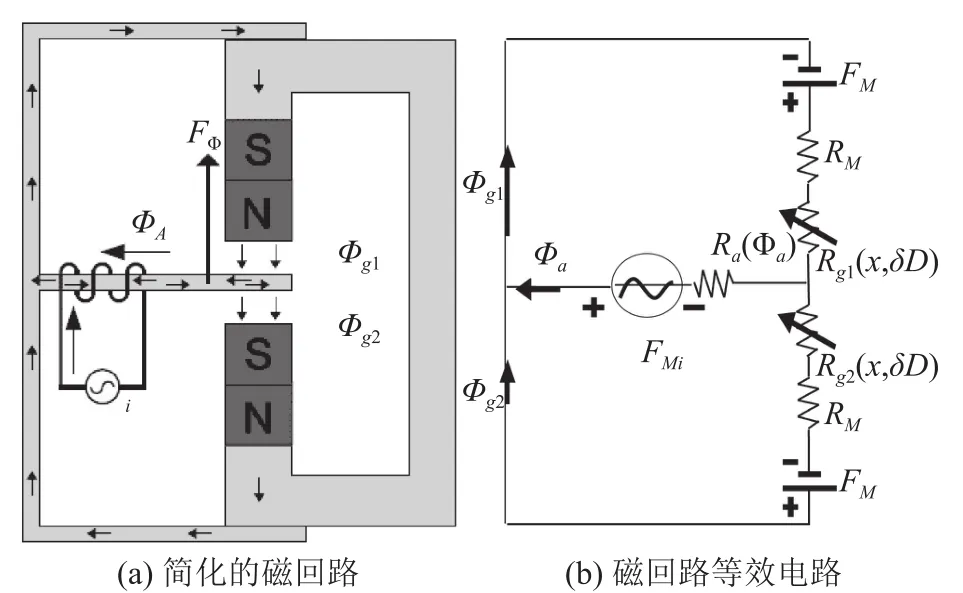
图2 平衡衔铁受话器简化的磁回路及其等效电路[9]Fig.2 Simplified magnetic circuit and equivalent circuit of BAR[9]

反电动势Uback可表示为[11]

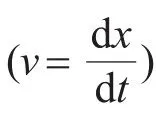
平衡衔铁所受的力，该力F可表示为[11]

式中，kΦ(x)为非线性补偿刚度系数，Tme(x)和Tme，d(x，i)分别为非线性传递系数和失真传递系数。由式(2)可知，当扬声器工作时，平衡衔铁所受的力不仅与流经线圈的电流有关，还与平衡衔铁的位移相关。与位移相关的力可称为动生磁场力。由于平衡衔铁是导磁材料，其运动会导致扬声器磁场特性变化，磁场特性的变化会导致平衡衔铁受到动生磁场力的作用。

平衡衔铁所受的力随位移变化的特性会对扬声器性能产生重要影响。平衡衔铁的有效刚度是其机械刚度与非线性补偿刚度系数的差值，非线性补偿刚度系数增加，会减小平衡衔铁的有效刚度，从而减小扬声器的共振频率；该系数的减小则会使振膜振幅增大，声压也会增大[11]。而该系数的增加会增加扬声器的不稳定性，这是因为有效刚度减小会使得平衡衔铁可能无法回到平衡位置。

2 数值仿真分析方法

由前文平衡衔铁受话器集总参数模型分析可知，平衡衔铁的运动会导致扬声器的磁场特性发生变化，在线圈上产生一个额外的反电动势，并使得平衡衔铁受到一个额外的磁场力作用。采用数值仿真分析方法仿真计算扬声器的声场特性时一般选用频域分析，直接的频域分析则无法考虑平衡衔铁运动对磁场特性的影响。

为此，本文提出一种基于COMSOL Multiphysics数值仿真分析软件的平衡衔铁受话器数值仿真分析方法，分为两个步骤：

(1)对平衡衔铁受话器的磁场特性进行稳态分析，并利用动网格技术，计算得到可随平衡衔铁运动变化的作用在线圈上的反电动势(速度电动势)和施加在平衡衔铁上的动生磁场力。

(2)创建平衡衔铁受话器电磁场、结构和声场的耦合分析模型，并利用前文稳态求解得到的可随平衡衔铁速度变化的速度电动势和可随平衡衔铁位移变化的动生磁场力，再进行频率分析，最终计算得到扬声器的声压级和阻抗。

无论是稳态分析，还是频域分析，数值仿真分析主要包括建立几何模型、定义材料参数、设置边界条件、网格划分、计算和结果后处理等步骤。

由于影响仿真分析结果准确性的主要因素包括几何模型、材料参数和仿真分析方法等三个部分，因此，下文以一款平衡衔铁受话器为例，首先简要介绍它的几何模型和材料参数，然后再详细介绍它的声压级和阻抗的数值仿真分析方法。

2.1 几何模型和材料参数

图3给出了一款平衡衔铁受话器的几何模型。平衡衔铁受话器具有几何对称性，因此只需建立其1/2几何模型即可。为了提高计算效率，模型中将带有花纹的金属球顶简化为平面，磁隙间距为0.1mm。

图3 一款平衡衔铁受话器的几何模型(1/2模型)Fig.3 Half geometry model of BAR

表1和表2分别给出了该扬声器各个部件的磁性材料参数和力学材料参数。由于在模型中简化了振膜的花纹，所以需要适当提高振膜的杨氏模量，使得简化后的振膜刚度可以等效包含花纹的振膜刚度。图4给出了平衡衔铁受话器磁轭(软磁材料)的BH曲线。其中，B为磁通密度，H为磁场强度，线圈匝数为350匝。

表1 平衡衔铁受话器部件的磁性材料参数Table 1 Magnet material properties of BAR

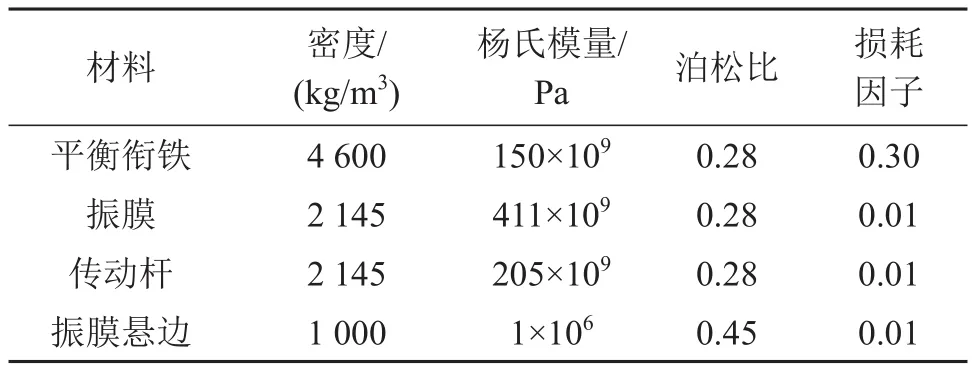
表2 平衡衔铁受话器部件的力学材料参数Table 2 Mechanical material properties of BAR

图4 磁轭(软磁材料)的BH曲线Fig.4 BH curve of soft iron

假设所有材料是各向同性的。对于磁性材料，需要给出磁通密度B和磁场强度H之间的本构关系，用剩磁Br和回复磁导率μrec定义永磁体本构关系[13-14]：

式中：μ0为真空磁导率。磁轭的磁通密度和磁场强度之间的关系是非线性的，需用完整的BH曲线来定义磁轭的本构关系。平衡衔铁的磁通密度和磁场强度之间的关系也是非线性的，但本文将其简化，仅用相对磁导率μr(常数值)来定义平衡衔铁的本构关系[13-14]：

对于平衡衔铁、传动杆和振膜等振动系统部件，均采用线弹性材料模型定义它们的应力应变关系。

2.2 平衡衔铁运动对扬声器特性的影响

为了仿真分析平衡衔铁运动对磁场特性的影响，平衡衔铁受话器的几何模型只需包含磁路和平衡衔铁，忽略振膜和传动杆等其他部件；假设金属外壳有一定的磁屏蔽作用，因而忽略外壳以外的空气域，仅建立外壳内的空气域。材料参数也只需定义磁路系统各个部件的磁性材料参数和平衡衔铁的力学材料参数。在平衡衔铁与外壳相接面上施加固定约束条件，在对称面上，通过定义磁矢势的面内分量为0和位移的法向分量为0，来分别设定磁场和结构的对称条件。在划分网格时，需对平衡衔铁适当加密网格。

在位于磁隙区域的平衡衔铁表面上添加力载荷(如图5所示)，平衡衔铁受力后会发生形变，可根据力的平衡方程计算得到平衡衔铁的位移大小。平衡衔铁作为导磁材料，其形变会改变磁场分布。为了模拟平衡衔铁运动(形变)对磁场分布的影响，模型中需要使用动网格技术，即网格将随着平衡衔铁的运动(形变)而变化。基于麦克斯韦方程组计算得到磁通密度分布。在平衡衔铁表面上加载不同大小的力，便可得到平衡衔铁运动到不同位置时的磁通密度分布。

图5 平衡衔铁的加载面图Fig.5 The loading surface diagram of the balanced armature

图6(a)和图6(b)分别给出了当平衡衔铁处于初始位置时及其从初始位置向上移动至磁隙间距的1/10位置时线圈所包围区域的磁通密度分布图。由图6可以看出，平衡衔铁位置(位移)的变化，会导致该区域磁通密度发生明显改变。磁通密度改变，会影响作用在线圈上感应电动势和平衡衔铁上所受到的力。

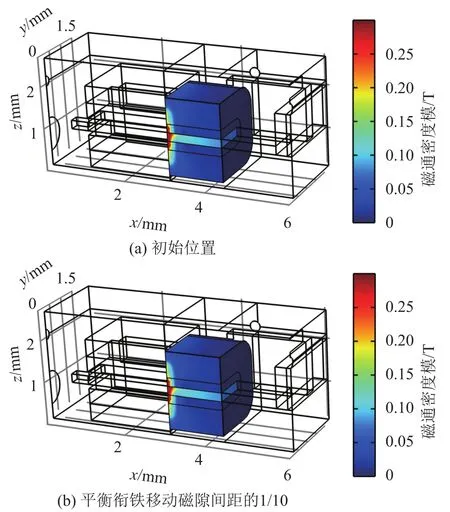
图6 平衡衔铁处于不同位置时的磁通密度分布图Fig.6 Diagrams of the magnetic flux density distribution when the balanced armature is at different positions

2.2.1 作用在线圈上的速度电动势

由式(1)可知，作用在线圈上的速度电动势Uv为

根据电磁感应定律，速度电动势Uv是磁通量Φ(x)对时间t的导数：

在平衡衔铁的位移比较小的情况下，假设线圈中的磁通量Φ(x)与平衡衔铁位移x呈线性关系；根据式(5)和式(6)，可以将Φ(x)与x的关系表示为

式中，系数Tme和a均为常数。当位移x较小时，近似认为非线性传递系数Tme(x)是一个不随x改变的常数Tme。

从前述稳态求解得到的仿真结果中选取几个平衡衔铁的位置，并根据平衡衔铁处于这些位置时的磁场分布计算线圈所包围面积的磁通量，再通过式(7)进行函数拟合，可以得到系数Tme和a。

将式(7)代入式(6)可得：

2.2.2 平衡衔铁上所受到的动生磁场力

平衡衔铁表面的电磁力密度矢量分量f为[14]：

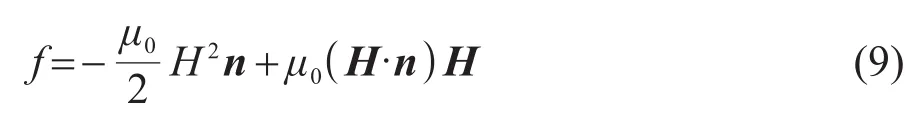
式中，n是表面单位法向矢量，H2=H2x+H2y+H2z。

图7给出了平衡衔铁在平衡位置时其所受的表面电磁力密度矢量分量的分布图，由图7可知，该作用力主要集中在磁隙区域对应的表面上。

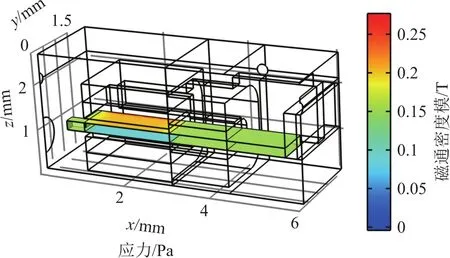
图7 平衡衔铁上表面应力分布Fig.7 Surface stress distribution of balanced armature

当平衡衔铁运动时，它与上下永磁体之间的距离会发生变化，距离越小，磁通密度越大，靠近永磁体的平衡衔铁表面应力会增大，远离永磁体的平衡衔铁表面应力会减小。

由式(9)可计算得到平衡衔铁表面应力(表面上每个节点的应力)随着位移变化的变化量，再对该表面应力的变化量求积分，即可得到(整个)平衡衔铁上所受到的力的变化量，也即动生磁场力FΦ：

式中：Δf是应力的变化量，S表示平衡衔铁表面。

由式(2)可知，平衡衔铁上受到的动生磁场力与位移相关，当平衡衔铁的位移非常小时，假设动生磁场力FΦ与位移x呈线性关系，即：

式中：系数kΦ为常数。当位移x较小时，近似认为非线性补偿刚度系数kΦ(x)是一个不随x改变的常数kΦ。

同理，从前述稳态求解得到的仿真结果选取几个平衡衔铁的位置，并根据式(10)计算对应的动生磁场力，再通过式(11)进行函数拟合，计算得到系数kΦ。

2.3 磁路、振动系统和声场的耦合分析

创建包含磁路和振动系统所有部件的平衡衔铁受话器的几何模型，因为它具有几何对称性，所以只建立其1/2几何模型即可。由于本案例的平衡衔铁受话器是作为受话器使用，因此，在仿真模型中，其声输出方式为711耦合器(压力场环境)。为提高计算效率，可采用特定的“阻抗边界”条件替代“711耦合器声腔(模型)”的简化方法，因而在仿真模型中并不需要建立耦合器声腔模型。图8(a)是包含耦合器声腔的全模型，图8(b)则是简化后的几何模型。对于图8(b)，只需要包含平衡衔铁受话器和小部分声腔，这样可以大幅降低计算量。采用表1和表2中的材料参数定义所创建模型中扬声器各个部件的材料参数。

图8 平衡衔铁受话器几何模型(含711耦合器)Fig.8 Geometry model of BAR(including 711 coupler)

在平衡衔铁与外壳相接面上施加固定约束。在对称面上，通过定义磁矢势的面内分量为0、位移的法向分量为0和加速度的法向分量为0，分别设定磁场、结构和声场的对称条件。空气域中除了与振动系统耦合面以外的边界面，全部假设为全反射边界。在小部分声腔与711耦合器的连接面上设定声阻抗，可等效711耦合器空气域对边界面上声压产生的影响，这个声阻抗Zin可以预先利用图8(a)全模型仿真分析得到，计算公式为

式中：Pin为输入端面处的声压有效值，Zin是与输入端面处空气体积流速Qin相关的声阻抗。合理划分网格，以保证计算频率范围内一个波长至少包含4～5个网格。

平衡衔铁受话器的磁路、振动系统和声场是相互影响的，在模型中需要正确定义它们的耦合作用。

对于磁场和结构这两个物理场，实际加载在线圈上的电压U是由外部加载电压U0和反电动势Uback两部分组成，而反电动势包含由于电流变化带来的反电动势Ui和由于平衡衔铁运动带来的反电动势(速度电动势)Uv，即：

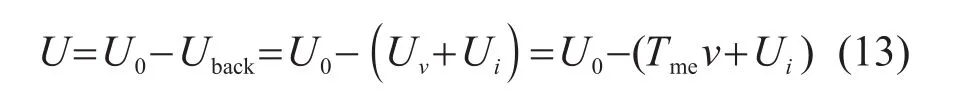
平衡衔铁所受到的力F是由线圈电流产生的感生磁场力Fi和因其自身运动而产生的动生磁场力FΦ两部分组成的，即：

对于结构和声场这两个物理场，振膜表面的加速度即为声源。同时，作用在振膜表面上的空气压强会使得振动系统受到额外的表面应力。

在线圈两端加载谐波扰动的电压U0，电压有效值为0.1 V。根据电磁感应定律，变化的电场会感应出磁场，磁路系统中除了原本的静态磁场以外，会再叠加一个谐波扰动的磁场。根据麦克斯韦方程组求解得到电场分布和扰动的磁场分布。根据式(12)可计算得到平衡衔铁所受到的感生磁场力Fi。平衡衔铁受力产生振动，根据结构运动方程[15]求解得到振动幅值。根据振动系统与声场的边界面上振幅(或加速度)，可计算得到声场分布。一般空气域的声场分析建立在理想流体媒质的波动方程[15]之上。而对于平衡衔铁受话器，在它的内部存在一些狭窄区域，不能忽略声波在狭窄区域中的粘滞特性。

如前文所述，为提高计算效率，几何模型中并没有包含711耦合器空气域，因此无法直接获取麦克风面处的声压级。利用已建立的几何模型声腔边界面(也即711耦合器输入端面)上的空气体积流速Qin和711耦合器空气域的转移阻抗Ztrans，可计算得到麦克风表面位置的声压pmic：

图9给出了该平衡衔铁受话器在频率为1 kHz信号激励下的声压级分布。由图9可知，在振膜与上盖之间的腔体内的声压最高，声波通过出声孔向外(711耦合器)传递。

图9 平衡衔铁受话器中的声压级分布图(@1 kHz)Fig.9 Sound pressure level(SPL)of BAR(@1 kHz)

3 仿真分析结果

通过本文提出的数值仿真分析方法可以较快地仿真计算得到平衡衔铁受话器的声压级和阻抗曲线。与此同时，作者还采用B&K Pulse系统测量了所研究的平衡衔铁受话器的声压级和阻抗曲线，为保证测量与仿真分析条件的一致，测量是在IEC711耦合器(爱宏AWA6162耳模拟器)压力场条件下进行的，符合IEC60318-4标准[16]。被测扬声器通过夹具安装在耳模拟器上，扬声器和夹具之间使用少量橡皮泥以防止泄露，图10(a)是被测平衡衔铁受话器，外尺寸为6.3 mm×4.3 mm×3.0 mm。图10(b)是被测扬声器通过夹具安装在耳模拟器上的照片。图10(c)给出了测量示意图，扬声器出声孔平面应与耳模拟器参考平面齐平。

图10 平衡衔铁受话器的测量Fig.10 Measurement of BAR

图11(a)和图11(b)分别给出了平衡衔铁受话器的声压级和阻抗的仿真分析结果和测量结果。由图11可知，在4 kHz以下，仿真分析结果和测量结果基本吻合；在高频段，两者趋势一致，数值存在一定差异。

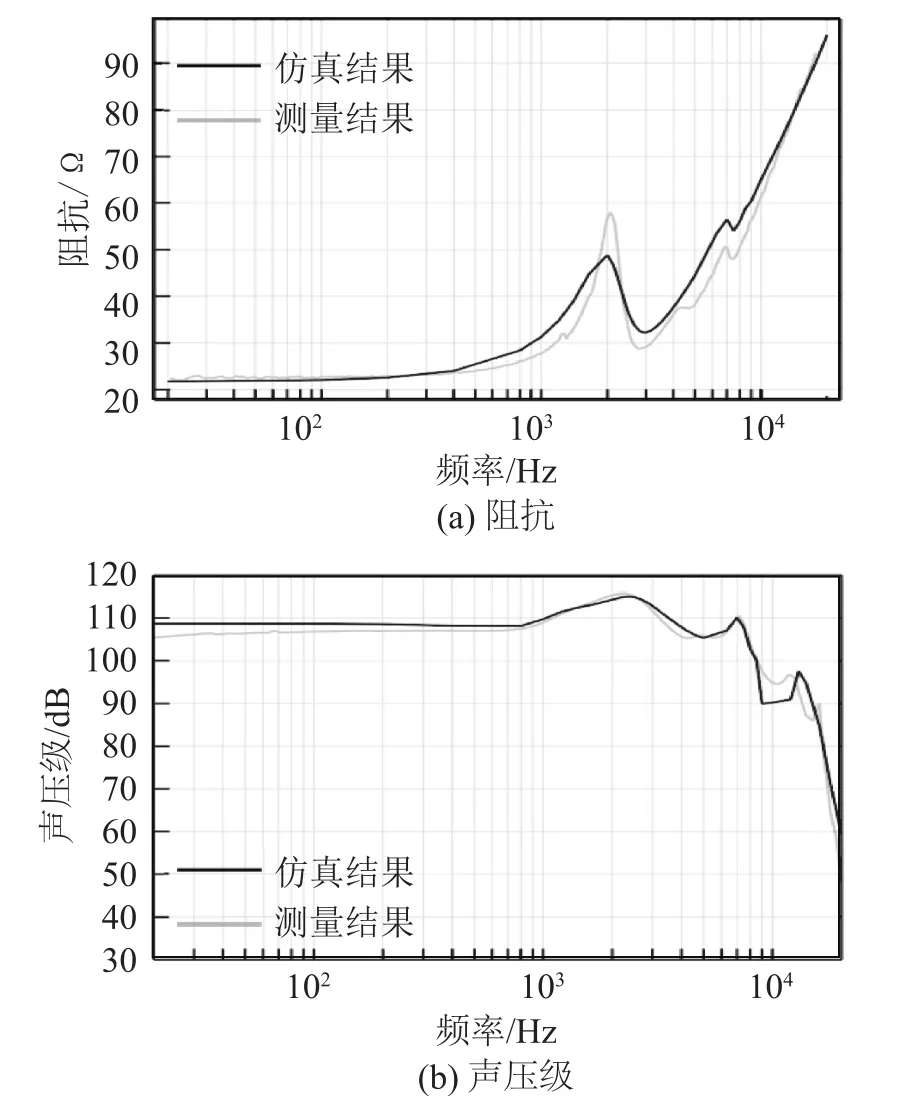
图11 仿真结果和测量结果Fig.11 Comparison between measurement and simulation

由图11(a)可知，在低频段阻抗值基本与直流阻抗一致；而在高频段阻抗值随频率增大而增大。这是因为由电流变化产生的感应电动势增大的缘故。感应电动势越大，电流越小，阻抗就越大。2 kHz频率附近的峰以及4、7 kHz频率附近的峰都与速度电动势有关，由于振动系统在这些频率附近发生共振(或谐振)，平衡衔铁的振幅相对较大，平衡衔铁运动引起的位置改变所带来的速度电动势也增大。同样，速度电动势越大，电流越小，阻抗也就越大。

由图11(b)可知，在低频段声压级基本为一稳定值，当频率大于1 kHz，声压级曲线出现多个谐振峰。低频声压级与振动系统的有效刚度密切相关，而动生刚度是有效刚度的重要组成部分。动生刚度越大，有效刚度越小，振幅则越大，低频声压级也就越高。2 kHz和7 kHz附近的谐振峰也与振动系统的共振(或谐振)相关，这些峰所对应的频率高低与动生刚度有关。动生刚度越大，有效刚度则越小，这些峰对应的频率也会越低。而14 kHz频率附近的共振峰则与此无关，它是由于711耦合腔的共振所引起的。

本文所提方法较为准确地仿真了可随平衡衔铁速度变化的速度电动势和可随平衡衔铁位移变化的动生磁场力。分析得到了阻抗共振峰和谐振峰，最终较为准确地仿真得到了低频声压级和声压级频响曲线上的各个峰。

4 结论

本文基于平衡衔铁受话器的集总参数模型分析，指出平衡衔铁运动会产生额外的反电动势和磁场力，提出了一种分步进行的平衡衔铁受话器的数值仿真方法。首先对平衡衔铁受话器的磁场特性进行稳态分析，计算得到可随平衡衔铁运动而变化的磁场力和反电动势；然后，建立电磁场、结构和声场耦合分析模型，并利用前面的稳态求解方法得到的可随平衡衔铁运动变化的速度电动势和动生磁场力，再进行频域分析，最终计算得到平衡衔铁受话器的声压级和阻抗曲线。仿真结果和测量结果基本一致。

平衡衔铁受话器的数值仿真分析方法还可以在以下几个方面进一步优化和完善：(1)深入研究平衡衔铁材料的磁特性，以建立更准确的非线性模型；(2)细致分析小体积声腔中的空气压强对振动系统的影响；(3)非线性和失真特性机理和高效仿真分析方法研究。