基于神经网络对水电站径流量及水库水位的预测研究

2022-12-05谢梓彬

水利科学与寒区工程 2022年11期

谢梓彬

(潮州市凤溪水库管理处，广东潮州 515656)

1 研究方法

图1为水库水位预测系统的示意图。如图可知，水电站库水位的预测因子包括历史径流量、历史水库水位和耗电量。基于人工神经网络将水库水位预测系统划分为两部分。一部分是将历史流量数据代入预测模块，然后预测未来一段时间内的大坝径流量。另一部分是将预测的径流量、历史库水位和耗电量三个数据一同代入大坝模型，以预测未来水库水位。

图1 水库水位预测系统图示

本文选择过去十年中的历史库水位、大坝来水流量和耗电量三组数据进行模型预测分析。其中，每组数据收集了大约10 300个，剔除一些无效数据后剩下大约94 000个可用数据。图2为2007年某河流的历史年径流量数据，由图可知一年中总有一些时段的流量值较高。由此可将径流数据按照时间划分为三个季节，如图3所示，且这种规律往往每年重复出现。文中选择三个不同季节的随机样本进行ANN训练，最后使用一个完整年份的样本数据进行验证。

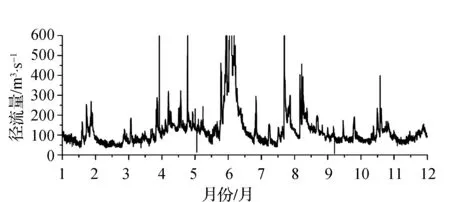
图2 2007年某河的历史年径流量数据

图3 根据某河的年径流量确定的季节情况

使用预测系统时，应将非平稳时间序列(NSTS)的流量数据转化为平稳时间序列(NSTS)的流量数据，且所调用的转换函数必须可以恢复原始数据，不会造成重大数据损失。鉴于以上条件，本文将所用数据对数化(即：ln(x1)，…，ln(xn))。该法可以减小大幅度的波动，且小幅度的波动也会得到更均匀的时间序列[1]。

此外，时间序列变换还可以加大功率谱密度(PSD)中的信号峰值，如图4所示。功率谱密度分析可以近似地确定信号的周期性和峰值的数量，有助于分别设置预测水平和ANN输入层神经元的最大数量。如图4中，预测时间节点可以设置为6 h、8 h、12 h和24 h，而进入神经元的最大数量设置为16。

图4 某河年流量16个峰值的功率谱密度

1.1 基于多步预测的人工神经网络

多步预测是一种估计未知变量直至水平的方法。这种预测方法主要基于离散时间序列的数据，且这些数据通常可以描述以往的变化趋势。图5为多步预测两个过程的示意图，首先使用以往离散时间序列的数据进行第一步预测，然后将第一步预测值并代入第二步再预测，最后获得两步预测的最终结果[2]。

图5(a)为闭环预测(CLP)，在第一个离散时刻k中，X表示一组最后可用的离散数据，其X的范围在[k-h，k]，并规定h大小取决于预测要求，Xp(k+1)则是用于下一个预测序列中的初始值。将Xp(k+1)代入下一个预测模块，获取最后的预测数据，重复以上操作，直至交互作用计时器达到h。

图5(b)为开环预测(OLP)，该预测输出仅基于历史数据。所以在离散时刻k中，X为一组可用的离散数据，该数据被作为预测系统的输入值，其取值范围是[k-2h，k-h]。在估计预测输出值Xp(k1)之后，将获取的数据集向前移动，然后进行下一次交互。重复以上过程直至满足h的预测。

图5 时间序列多步预测系统示意图

CLP法是根据前一部分的预测值获取最后的预测输出值。CLP法可能会导致预测中的累积误差，而这在OLP法过程中并不存在。但由于CLP法不像OLP法那样过于依赖于训练阶段和次数，所以CLP预测法可以随时调整水位。

1.2 基于人工神经网络的建模

在控制和自动化领域，动态系统的识别是基础。后者可以基于数学建模，但当系统复杂且未知时，建模将变得困难。研究发现根据已获取的输入和输出数据使用统计技术，可以成功建立非线性动力系统的模型，如：NARMA(非线性自回归移动平均)。此外，ANN也可以用于系统建模，在扰动前ANN获得模型相比多项式建立的模型更加稳定，因此ANN模型预测效果相对更好。

本文采用ANN模型，且使用ANN训练方案获取水电站模型如图6所示。由图6可知，实际坝段是将历史的径流量和耗电量数据关联到离散输入信号X(k)，同时将历史库水位数据作为系统的实际输出信号Y(k+1)，接着把上述三个信号作为本次ANN训练集的离散输入信号。把预测的水库水位Yp(k+1)作为输出信号，然后将预测的水库水位和实际输出的水库水位Y(k+1)进行比较，最后获取两者之间的误差。其误差用于调整ANN内各参数的权重，使其结果更接近于实际情况。由于使用计算机模拟时内存占有率高，所以本文采用BFGS算法进行权重的数值优化，该法可以有效解决内存占有率高的问题还能迅速达到模型计算的收敛[3-4]。

图6 ANN模拟训练实际大坝的图示

综上所述，经过训练的神经网络可以估计实际大坝的动态,如图7所示。本文利用ANN建立大坝模型。其中，由于模型中没有水库水位的实际数据，所以对水库水位的预测输出信号Yp(k+1)必须反馈给大坝模型。由于预测值均基于实际值，所以这里可能再次产生累积误差。

图7 训练后的神经网络预估库水位图示

2 方案实施

本文首先对流量数据进行PSD分析，然后再估计ANN入口层中神经元的最大数量。研究中ANN采用一个输入层两个隐含层的拓扑结构，并定义输入层和第二隐藏层中的神经元个数必须相等。考虑到图4中的峰值数量，对ANN进行几次训练，以确定不同季节的神经元最佳配置。在这一阶段，由于BFGS算法的快速收敛，所以每个ANN配置只需进行100次训练。表1为冬季不同人工神经网络训练实例结果。其中，表1第6行是ANN最好的配置选择，因为它的验证误差最小，且输入神经元的数量未超过16个。

因此，从季节类型(见图3)与多步骤预测方法(见图5)的组合中，可以获得6组预测因子。在不同预测水平，CLP法的预测值不像OLP法那样过于依赖样本训练。因此，CLP法可以用于不同的预测水平，而OLP法需要针对不同水平进行多次不同的样本训练。

由图6的训练方法，获取夏季、初冬季和正冬季三个季节的大坝模型。如上所述，用于ANN训练和大坝模型学习的历史数据包括径流量、耗电量和水库水位。首先将数据代入模型中，然后使用BFGS算法优化ANN的结构，并以误差最小确定最佳的ANN大坝模型。最后根据径流预测模块的输出值、图7所示的耗电量和最佳大坝模型来估计未来的水库水位。由于大坝模型不依赖于任何预测水平，所以该模型与同一季节的任何水流预测均相兼容。

表1 不同神经网络在正冬季的训练结果

3 结果与分析

本文针对每日不同的预测水平，通过22 d的现场实际监测获取试验结果。为了确定更合适的预测水平，根据预测期间的准确性对结果进行比较。当流量和水库水位预测的均方根误差(RMSE)分别≤± 8 m3/s和± 0.5 m时，说明流量和水库水位符合预测的标准。

如上所述，通过两种多步骤实施的预测方法(见图5)与三个气候季节(见图3)相结合的形式，获得了6个径流量预测因子。由于试验监测是在两个季节过渡期进行，所以使用冬季和夏季两个季节相互比较。表2为夏季不同试验水平径流量的预测结果。如表2所示，当预测水平较小时(如3 h和6 h)预测的成功率上升，RMSE减小(SD离散程度较高)。此外，通过比较成功预测的百分比，发现同一季节和预测水平，CLP法预测值优于OLP法预测值。而如图8所示，相同水平不同季节条件下，CLP法夏季的预测比初冬季的预测效果更好。然而，最高的预测成功率(大于80%)仅出现在低预测水平(3 h)。图9(a)和图9(b)分别为在初冬和初夏两个季节中CLP法对每日径流量预测的RMSE，同时还绘制了径流量预测的标准线(灰色虚线)。

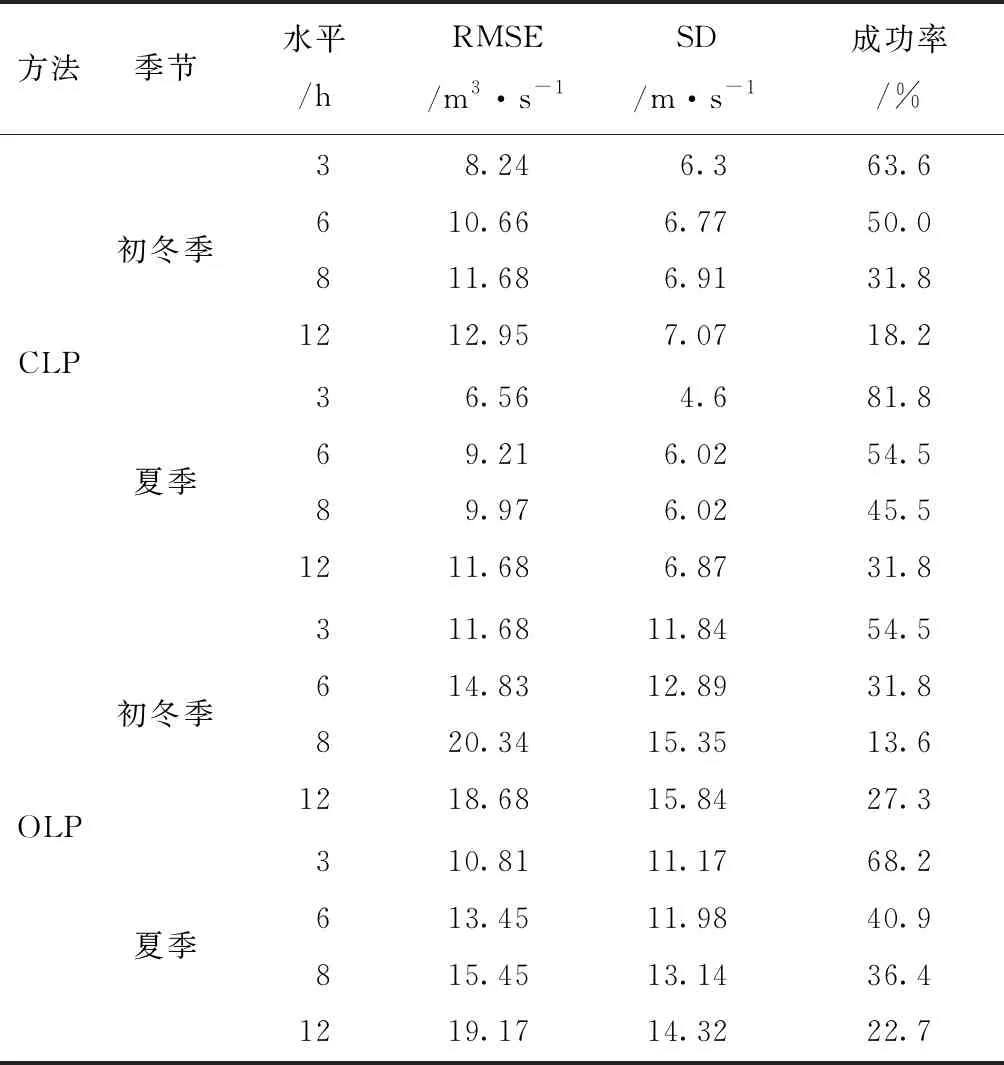
表2 径流量预测结果

图8 CLP法预测径流量的成功率对比情况

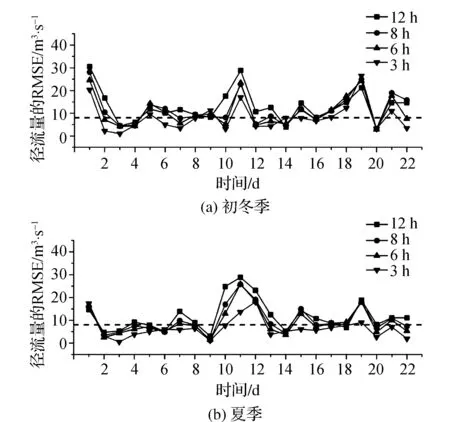
图9 CLP法对每日径流量预测的RMSE

图10 CLP法每日水库水位预测的RMSE

如图7所示，将径流量的预测结果用于给定生产定额条件下未来水库水位的预测。因为CLP法预测性能及其效果均高于其他预测方法，所以本文选择CLP法的预测结果。图10(a)和图10(b)分别是冬季和夏季22 d试验期间每日水库水位预测的RMES，根据RMSE最小成功绘制出预测的水库水位基准线。其中，水库水位的预测结果和正确预测百分比如表3所示，根据两个季节水库水位预测中的平均RMES和SD，发现在预测水平较短和数据较为集中时，预测的水库水位呈现显著降低的趋势。同时，通过分析预测的成功率和表2中的径流预测结果可以看出水库水位的预测具有显著性提高。然而，由图11发现在夏季预测时采用CLP方法(用于径流)和大坝模型(用于水库水位)预测的效果略高于初冬季。

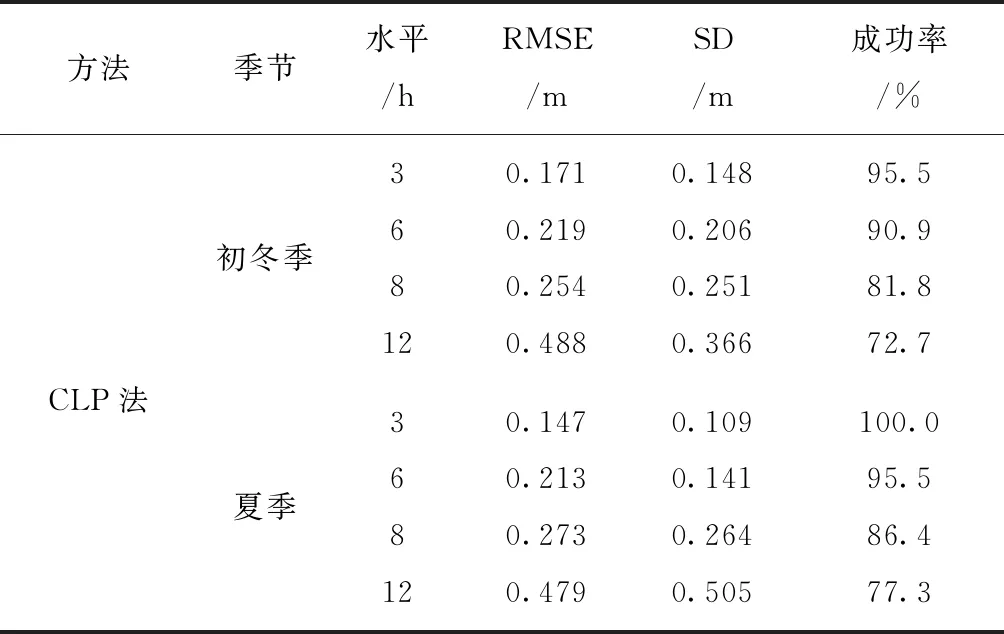
表3 水库水位预测结果汇总

图11 CLP法与大坝模型水库水位预测成功率比较

尽管所有预测水平的预测成功率均超过了70.0%，但同一水平的径流量预测结果并不高。其中，图12为径流量预测系统(CLP方法)与水库水位预测系统(CLP +大坝模型)夏季预测成功率的对比，其中水库水位的估算是基于同一气候季节的径流预测结果。通过以上对比表明，“大坝模型”提高了水库水位的预测能力。即使在径流量预测结果不太准确的情况下，水电站的大坝也可以减轻人为自然状态下的扰动作用。