基于PSO-Elman修正模型的年径流预测
2022-12-05王文川,王莉芳,郭安强
王 文 川,王 莉 芳,郭 安 强
(1.华北水利水电大学 水资源学院,河南 郑州 450046; 2.河南省鹤壁水文水资源勘测局,河南 鹤壁 458030)
0 引 言
径流模拟因受多种因素的影响,其序列具有较强的非确定性,一直是水文研究领域的难点[1]。为了提高径流模拟精度,人工智能方法比如人工神经网络、灰色预测法、支持向量机和小波分析等逐渐应用到径流预报中[2-5]。如Snieder等[6]利用人工神经网络进行流域径流模拟,郑世武等[7]将灰色系统理论应用于黄河花园口站的年径流模拟,Ozgur等[8]提出小波支持向量机组合模型用于月径流模拟。人工神经网络(Artificial Neural Network,ANN)[9]中的Elman神经网络模型在预测径流序列方面因在结构上增加了一个承接层构成反馈相比传统方法更具准确性。但由于径流模拟受到降雨、蒸发和人类活动等因素的影响,结合多种方法优点的组合预测模型以及改进优化模型的预测精度要优于单一模型。因此,许多学者将结合多种方法优点的耦合预报模型以及优化模型用于径流预报。李志新等[10]利用遗传算法的全局优化能力来优化传统网络初始参数值,耦合构建了GA-Elman年径流预测模型,结果表明通过遗传算法改进传统神经网络可明显提升径流预测精度,缩小误差。徐留兴等[11]采用改进的Elman递归神经网络对紫坪铺站的月径流数据进行预测,并与传统Elman模型预测结果对比,结果表明可将该模型应用于月径流预测领域。由于传统Elman神经网络模拟训练时采用的算法普遍是梯度下降反向传播法,导致模型训练预测时收敛速度慢,达不到高效要求,且训练过程中容易收敛于局部极值。针对上述问题,本文利用粒子群算法(Particle Swarm Optimization,PSO)的全局搜索优化能力来优化改进传统Elman网络模型参数(权、阈值和隐含层神经元个数),通过优化算法弥补其在处理多因子径流序列模拟时存在的缺陷。
马尔科夫链(Markov Chain,MC)可以表述为随机过程的动态变化,可通过不同状态之间的状态转移概率来预测其未来状态,适合于随机波动较大的预报问题[12],可以用来修正预测结果。本文基于收集的呼兰河兰西水文站的实测径流深数据,利用传统Elman神经网络模型和PSO优化后的Elman模型进行多因子径流深序列预测,并采用MC对耦合模型初始预测值进行修正,构建了基于马尔科夫链修正的PSO-Elman多因子径流模拟模型,进而改善径流模拟效果。
1 研究方法
1.1 Elman神经网络
Elman神经网络是在传统BP神经网络[13-14]模型结构的基础上改进增加了一层反馈层(承接层)共4层结构的一种局部回归模型,其中新增的承接层作为延时算子起到动态反馈作用,进而提升模型模拟预测性能[15]。
输入到输出层的反馈过程中,Elman神经网络通过不同的反向传播法进行优化改进模型参数。相较于只有优化权值作用的传统BP网络前馈结构而言,Elman模型增加了一层反馈结构,此结构可将过去某一状态和未来某一状态共同作为隐含层的输入值,传递函数普遍为非线性函数,进而通过该非线性函数确定隐含层神经元个数,相应的模型拓扑结构如图1所示,该网络状态空间的表达式如下:
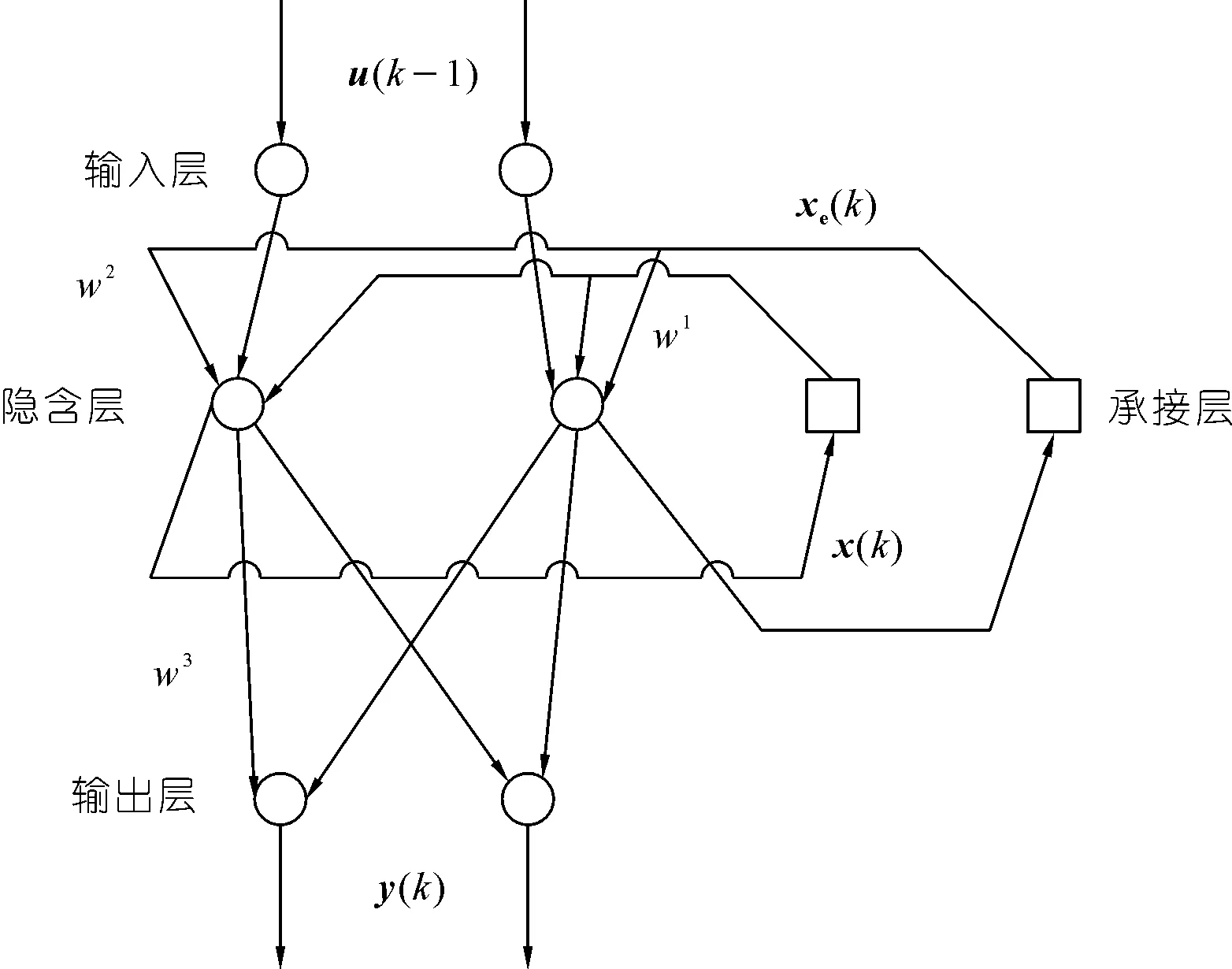
图1 Elman神经网络拓扑结构
y(k)=g(w3x(k))
(1)
x(k)=f(w1xe(k)+w2(u(k-1)))
(2)
xe(k)=x(k-1)
(3)
式中:u表示输入神经元向量;y表示输出神经元向量;x表示隐含层神经元向量;xe表示反馈状态向量;w1表示输入层到隐含层的连接权值;w2表示隐含层到承接层的连接权值;w3表示隐含层到输出层的连接权值;g和f分别表示输出层和隐含层神经元传递函数。
1.2 粒子群优化算法
粒子群(PSO)算法是由Kennedy和Eberhart提出的一种具有全局搜索能力的智能优化算法[16-18]。优化流程如图2所示,粒子群算法更新公式为
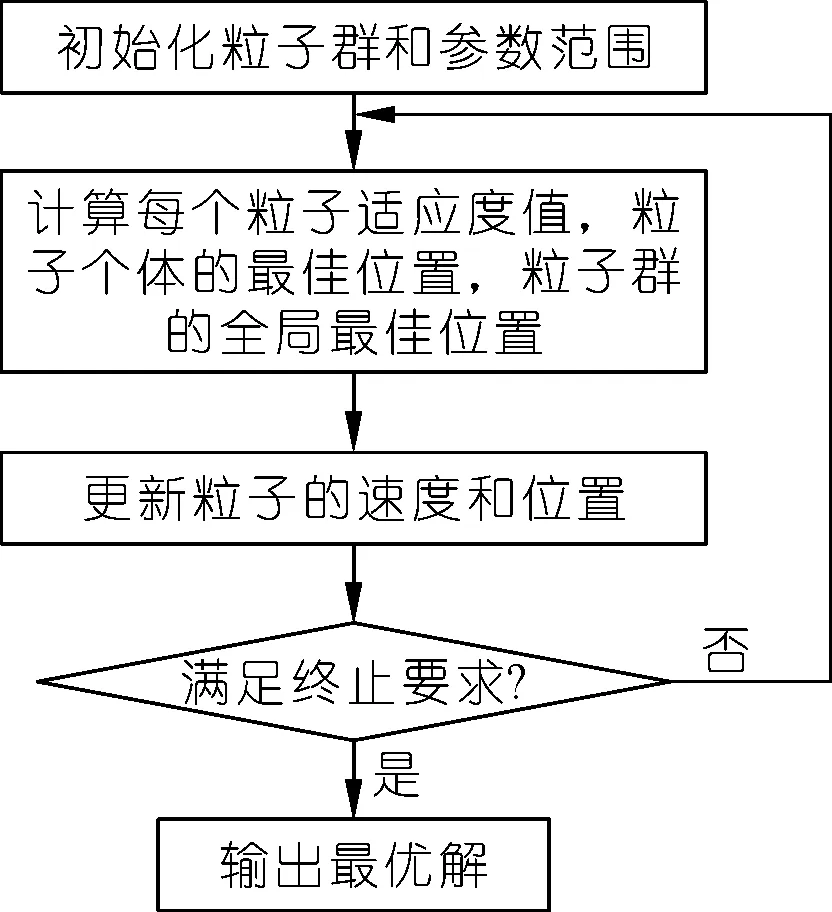
图2 粒子群算法流程
(4)
xt=xt-1+vt
(5)
式中:t为迭代数;x为迭代时粒子的位置;v为迭代时粒子的速度;r1,r2为分布于(0,1)区间的随机数;c1,c2为增速因子(正实数);pbest为个体粒子搜索到的最优位置;gbest为所有粒子搜索到的最优位置;ω为惯性权重因子,取值范围为(0,1)。
1.3 马尔科夫链
马尔科夫过程是一种随机动态变化过程,原型为马尔科夫链模型,具有未来状态不依赖于过去状态的特性。在已知状态的条件下,根据状态转移推求未来状态[19]。模型修正步骤为:① 根据实测值与预测值的相对误差的绝对值,划分样本空间状态;② 确定状态转移概率矩阵P;③ 根据矩阵P求解未来状态的概率分布。
马尔科夫链修正预测实质上是一个区间预测,即确定了残差变化范围和转移概率后,进而求出每个状态的概率之和,其中概率和最大的那个状态就是预测值误差所在的状态。利用龙浩等[20]修正位移预测值的公式来修正PSO-Elman模型初始预测结果:
(6)

2 模型建立
传统Elman动态神经网络预测建模时初始的权值和阈值一般由伪随机数初始化,使得训练好的模型性能不稳定,且其采用的算法存在缺乏全局搜索优化能力的缺陷。因此,本文利用具有改善传统Elman神经网络算法缺陷能力的PSO算法进行优化改进,提出了基于PSO优化的Elman多因子径流模拟模型,改善Elman神经网络的预测效果,然后运用马尔科夫链修正公式(6)来修正耦合模型初始预测结果,得到最终模型预测值。
基于马尔科夫链修正的PSO-Elman模型建模思路如图3所示,具体步骤如下:

图3 基于马尔科夫链修正的PSO-Elman模型
(1) 输入归一化的预报因子数据与实测径流深数据,划分训练集与测试集。
(2) 采用经验公式结合非线性传递函数设置隐含层神经元个数:
(7)
式中:m为隐含层神经元个数;n为输入层节点个数;l为输出层节点个数;α为1~10之间的随机常数。
(3) 选取耦合模型的适应度函数。本文的PSO-Elman多因子径流模拟模型选取训练集和测试集整体的均方根误差为适应度函数。
(4) 初始化最大迭代次数N,种群规模n,c1,c2,ω参数。
(5) 初始化算法的种群位置。速度更新和位置更新直至满足终止准则即达到最大迭代次数N,终止优化算法。
(6) 将PSO优化后的个体即参数值,赋给Elman神经网络,利用PSO-Elman模型进行模拟预测,并分析最终预测结果。
(7) 运用马尔科夫链修正耦合PSO-Elman模型的初始预测结果,得出修正后的最终径流预测值。
3 实例应用
3.1 研究区概况及数据来源
呼兰河发源于小兴安岭西南麓炉吹山,是松花江的一条支流,河长523 km,流域面积为35 683 km2。流域多年平均径流量为41.29亿 m3,多年平均降水量约570 mm,降水主要集中在汛期(6~9月),约占全年的78%,并以7~8月最集中,约占全年的60%。本研究基于收集的位于呼兰河下游的兰西水文站1959~2014年的径流深数据、降雨数据、蒸散发数据以及平均气温、平均气压等20种预报因子资料,运用SPSS 26.0统计软件对上述影响因子分别进行Mann-Kendall(M-K)显著性和Spearman相关性分析,结果如表1所列。分析径流深与上述20种预报因子间的相关关系,选择前一年相关性较强的极大风速、平均气压、最高气温、月日照百分率、降水量、日照时数、蒸散发量等7种预报因子作为传统Elman模型、PSO-Elman模型的输入,当年的径流深数据作为模型输出;简单线性回归模型则选择前一年的年降水数据作为模型输入,当年的年径流深数据作为模型输出。径流预测模型均选择1960~2003年前34 a的样本作为训练样本构建并训练神经网络,2004~2014年的数据作为测试样本进行径流预测。

表1 预报因子显著性及相关性分析
3.2 网络训练情况
Elman神经网络拓扑结构因缺少完整的理论指导,隐含层神经元个数按照经验公式(7)结合某种非线性适应度函数来选取。根据径流预测模型模拟结果的均方根误差(MSE)值的大小,选取传统Elman模型和PSO-Elman耦合模型隐含层神经元个数都为3,其对应的均方根误差值较小,结合输入层神经元个数7和输出层神经元个数1,确定本研究的模型结构为7-3-1。本研究采用的PSO算法初始参数设置为:最大迭代次数N=100,种群规模n=10,学习因子c1=c2=2,惯性权重因子ω=0.9。
3.3 马尔科夫链校正预测值
根据优化后的PSO-Elman耦合模型模拟训练得到训练期和测试期所有样本的初始预测值,进而分析所选站点训练期样本预测数据的平均相对误差绝对值分散情况,划分为[0,10%),[10%,50%),[50%,100%),[100%,200%)共4个马尔科夫链校正状态区间。通过上述4个马尔科夫链校正区间确定该站点训练期每一个径流深数据的平均相对误差绝对值所处的一种状态,并计算下一状态的转移概率矩阵如下:
(8)
通过矩阵P可计算得出每个状态的概率之和,其中概率和最大的那个状态就是预测值误差所在的状态,即为状态区间[10%,50%)。进而确定状态向量并通过式(6)对PSO-Elman耦合模型测试期的径流深预测值进行修正,故得到经MC修正后的兰西水文站测试集的最终预测结果。根据相同的实测训练期样本数据和测试期样本数据,分别采用简单线性回归模型、传统Elman模型、PSO-Elman模型和MC校正的PSO-Elman模型进行训练预测,最终预测值与实测径流深数据的对比分析如表2所列。

表2 MC校正的PSO-Elman、PSO-Elman、传统 Elman模型、简单线性回归模型预测径流深对比
3.4 结果分析
为进一步比较4种模型预测方法的预测效果差异,将不同模型的径流深预测值和预测值的平均相对误差绘制成折线对比图,如图4~5所示。本文选用合格允许误差为20%,测试集2004~2014年的预测值表明,PSO-Elman组合模型预测精度要优于单一传统Elman模型,均方根误差由57.60 mm降低至40.23 mm,降低了30.2%;测试样本的平均相对误差由77.89%降低至39.68%,降低了49.1%,确定性系数由0.32提升至0.67;PSO-Elman模型较简单线性回归模型均方根误差由64.60 mm降低至40.23 mm,降低了37.7%,测试样本的平均相对误差由102.20%降低至39.68%,降低了61.2%,确定性系数由0.14提升至0.67;经马尔科夫链模型修正后的PSO-Elman模型预测精度显著提高,测试样本的均方根误差由40.23 mm降低至19.22 mm,降低了52.2%,平均相对误差由39.68%降低至16.78%,降低了57.7%,确定性系数由0.67提升至0.92。预测效果得到显著改善,为提高径流预测精度提供了一种新方法。
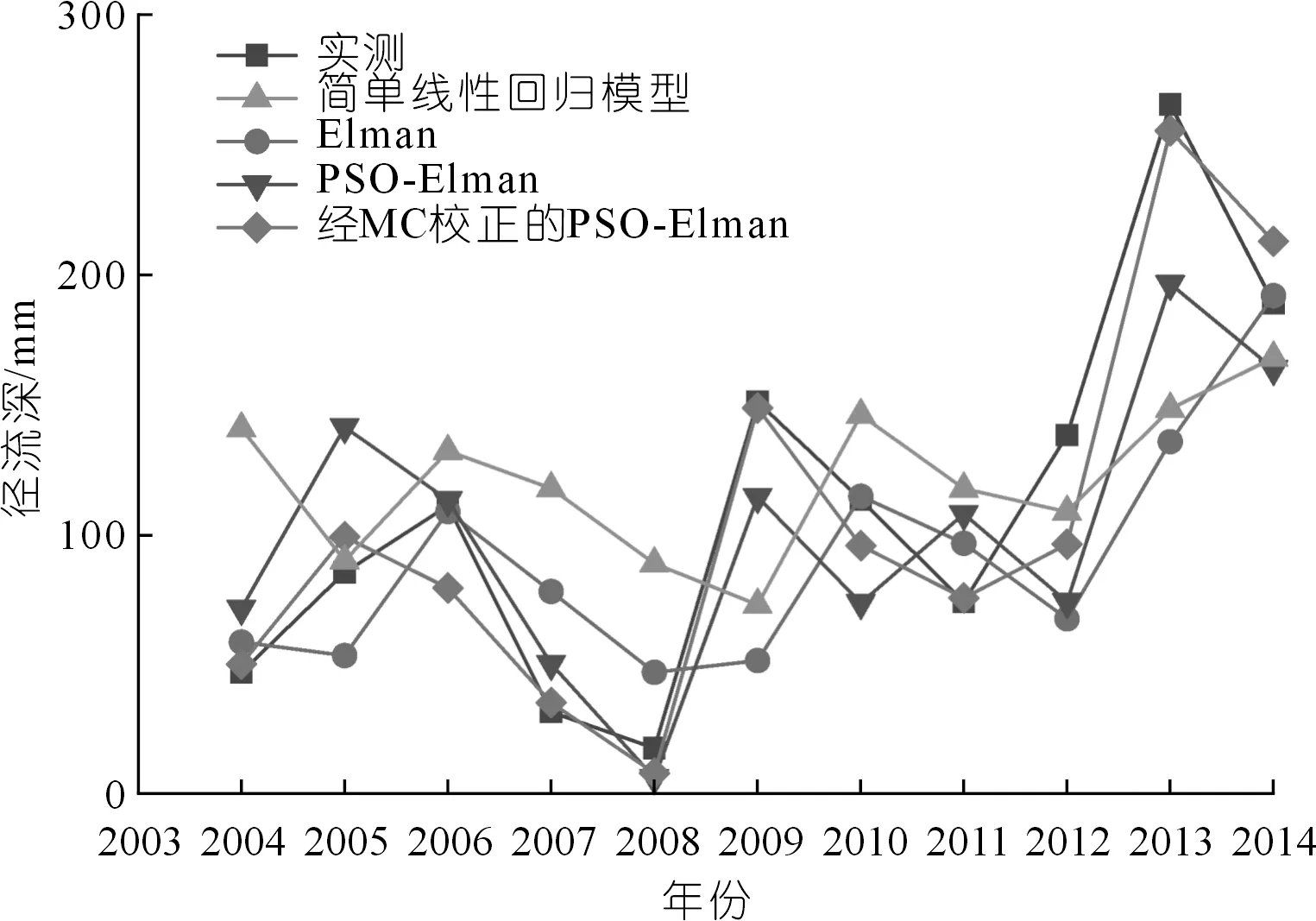
图4 不同模型径流深预测值对比

图5 不同模型径流深预测值相对误差对比
4 结 论
本文通过PSO优化Elman模型参数,进而利用马尔科夫链模型对预测结果进行修正,建立了基于马尔科夫链的PSO-Elman多因子年径流模拟模型,主要结论如下:
(1) 通过PSO优化Elman模型参数,二者耦合建立了PSO-Elman多因子径流模拟模型,将收集的影响因素数据作为预报因子,实测年径流深作为预测对象,可用来模拟兰西水文站年径流深演变过程,较Elman模型具有更高的精度。
(2) 运用马尔科夫链修正模型对PSO-Elman预测结果进行修正得出最终预测值,结果表明修正后的模型能有效提高原始模型预测精度,弥补了PSO-Elman模型难以预测径流随机波动较大的不足。
(3) 利用马尔科夫链和粒子群算法改进传统神经网络的训练算法可明显缩小预测误差,模型预测精度有显著提高,为长期多因子径流模拟研究提供了一种新途径。
