高精度凝胶物理特性分析系统研究

石萌萌，高炜欣，李杰

（1．西安石油大学 陕西省油气井测控技术重点实验室，陕西 西安 710065；2．西安石油大学光电油气测井与检测教育部重点实验室，陕西 西安 710065）

引 言

凝胶作为化学堵漏剂具有成胶时间可控、成胶强度高等优点，已成为石油开采、地质矿采开发等相关领域处理地层复杂情况最可靠、经济的堵漏剂之一［1-2］。对其物理性质研究有助于在实际应用中选择合适的堵漏剂参数，继而保证现场堵漏效果和提高产量。凝胶的物理性质主要包括密度和黏度等，其中黏度体现了流体分子间的相互作用，是凝胶生产及使用时的重要参数，黏度的准确测量对石油石化等领域保证安全生产、提高产量具有至关重要的意义。

黏度的测量主要采用传统的振动法、落体法和旋转法［3］。这些测量方法均为接触式测量，导致样品与容器接触发生反应，且自动化程度低，导致测量精度和效率偏低。鉴于此，非接触测量成为当前研究的热点。MERT等［4］依据圆管中流体影响声能衰减程度与其黏度、声音频率等有关，提出了基于圆管流体中的平面波的声阻抗测量流体黏度；随着光学技术的发展，YOSHITAKE等［5］基于激光诱导表面应力技术，分析激光诱导的延迟时间、表面应力与流体黏度之间的关系求解黏度值；HASSAN等［6］利用RFID-IC技术和集成电路对流体的声波信号进行分析，并将声学黏度和动态黏度联系起来，实现了非接触式的黏度在线测量；SAVENKOV等［7］提出使用非接触式的空气流体动力学技术使得被测流体的表面产生变形，并用光学传感器检测产生形变的距离，进而实现自动化测量黏度；NEFF等［8］设计了一种基于压电陶瓷驱动自由悬浮矩形振动板的黏度测量系统，由液体中因振动产生阻尼来求取黏度值；JANG等［9］提出了一种基于能量耗散的黏度测量技术，并利用有效黏度和有效剪切速率反映真实黏度，该方法适用于非牛顿流体黏度的现场监测。随着机器视觉技术的逐步成熟，基于图像处理技术实现自动化、非接触式、高精度的测量成为可能。叶云舟等［10］利用机器视觉技术对凝胶图像感兴趣区域（Region of Interest，ROI）进行阈值分割以提取有效信息，进而获取参数，求解凝胶黏度。

通过已有的文献研究可以发现，针对黏度的测量方法研究主要分为两种：（1）对传统方法进行改进；（2）基于新技术，研究高精度及非接触测量方法。文献［4］-［9］所提方法虽可完成非接触测量，但适用范围较窄，且测量系统复杂、成本昂贵；文献［10］为简单快速的黏度测量提供了新思路，但其研究在计算重要参数位移时，未考虑凝胶受到压力驱动时因实验器材等原因会发生畸变从而产生较大误差，最终导致黏度测量结果精确度低且系统鲁棒性差。为此，本文提出一种将传统毛细管法与机器视觉技术相结合实现黏度自动化测量的方法。

1 黏度测量原理

1．1 毛细管法

毛细管法是一种操控少量流体发生层流，用泊肃叶定律计算黏度的方法。其测量特点是使用少量凝胶即可完成测量，并且小尺度的测量更能揭示凝胶的物理特性（如黏度），将其与计算机技术结合可实现便携式高精度的自动化测量。

1．2 层流现象

层流指流体做层状流动，凝胶在毛细管中做低速流动时会呈现层流状态。泊肃叶定律（如图1所示）指出不可压缩牛顿流体在圆管中作水平定常层流时，各物理量之间的关系为：

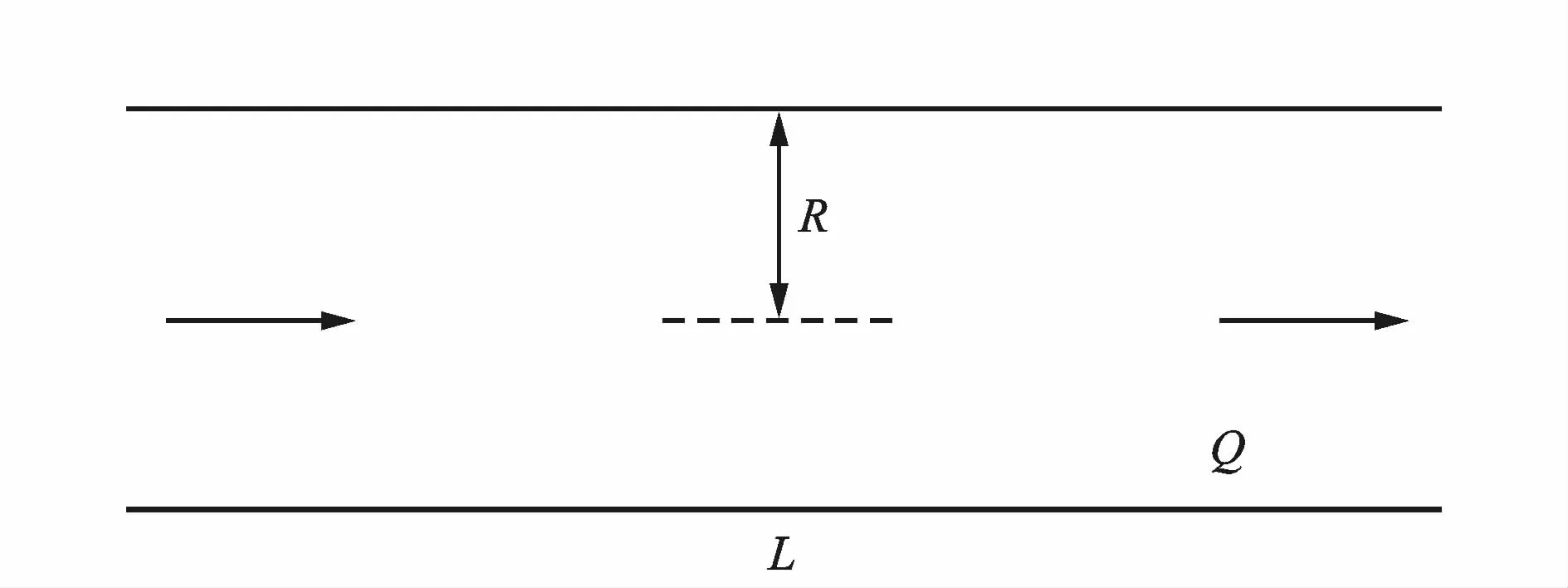
图1 泊肃叶定律示意图Fig．1 Schematic diagram of Poiseuille"s law

式中：Q为体积流量，mm3；ΔP是圆管两端压强差，mPa；R为圆管半径，mm；η为流体的黏滞系数（即黏度），mPa·s；L为流体总长度，mm。

由式（1）可得黏度

因Q为被测毛细管中凝胶的单位体积流量，故：

式中：ΔV为毛细管中凝胶样品单位时间Δt内流动的单位体积。

由于凝胶样品在毛细管中形态为圆柱型，故单位体积

其中，Δl为毛细管中凝胶样品单位时间Δt经压力作用后产生的位移，则单位时间Δt产生的单位体积流量

故可得到本文凝胶黏度测量方法的直接求解公式：

其中：R为毛细管半径，mm；L为毛细管内凝胶样品的总长度，mm；Δt是设置的间隔采集时间，s；ΔP为上位机经串口通信实时采集的压强差，mPa。据此可知，对黏度η精确求解的本质是对间隔时间Δt凝胶位移Δl的精确测量，最后将各参数值代入式（6）中即可得到被测凝胶样品的黏度η。

测量原理中各参数如图2所示。

图2 参数示意图Fig．2 Schematic diagram of parameters

1．3 像素的度量换算

在图像处理过程中测量距离通常为像素点数，而实际计算中Δl使用的通常为公制单位毫米，故应求解像素与毫米的换算系数，记作ξ。在本文中毛细管直径为2R，在阈值分割后定位毛细管上下壁，求其像素差，记作Δδ，故有：

在图像分析时，记每组像对凹液面之间的像素点数差值为Δd，故可得

2 测量系统设计

根据上述测量原理，设计了测量系统（图3），主要由机器视觉模块、加压模块和图像处理模块3部分组成。

图3 测量系统示意图Fig．3 Schematic diagram ofmeasurement system

机器视觉模块由高清工业相机、光学显微放大镜和毛细管夹持器组成，实现对毛细管凝胶运动图像采集；加压模块选择支持串口通信的驱替泵，实现驱动空气推动凝胶匀速移动；图像处理模块为上位机程序，完成实时压力值采集、图像采集、停止采集等控制事件，最后完成凝胶黏度值的自动计算。

图像质量是影响凝胶黏度高精度测量的重要指标。相机分辨率是评价图像质量的重要参数，分辨率越高则获取图像目标区域的细节越多，从而图像分割时分割精度会越高，故高分辨率的工业相机是实现高精度测量的必然选择。本文选择的工业相机性能参数见表1。

表1 相机性能参数Tab．1 Performance parameters of camera

在该系统中，毛细管半径选择为1 mm，可以保证凝胶在内部流动呈层流状态，此外压力泵推动凝胶流动的压力应选择较低值。在此条件下可以暂时忽略泊肃叶定律对被测液体必须为不可压缩牛顿流体的要求，而使用该定律来计算。

另外，在测量系统中，相机分辨率和镜头焦距是评价图像质量的重要参数，较高的分辨率以及合适的焦距能获取目标区域更多细节，目标区域细节的明显程度则体现了图像质量的优劣。由像素与实际物理距离的关系可得相机分辨率应不低于600×400，依据实际视野范围选择25 mm焦距的镜头即可满足实验要求。

测量具体流程如图4所示。

图4 测量流程图Fig．4 Flow chart ofmeasurementmethod

3 凝胶图像处理

毛细管凝胶图像的预处理是实现黏度高精度测量的关键环节，清晰的图像有利于提高边缘信息提取的精度。图5为采集到的毛细管凝胶图像。

分析图5可知，毛细管凝胶图像背景简单、上下壁边界清晰，但凹液面边界存在较大噪声，故需对凝胶原始图像进行针对性预处理，以分割出清晰的凝胶边界曲线。一般采用的技术有图像去噪、图像增强、边缘检测以及图像分割等。图像的处理过程如图6所示。

图5 凝胶原图像Fig．5 Original image of gel

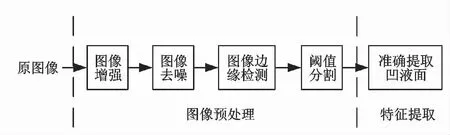
图6 图像处理过程Fig．6 Image processing process

3．1 图像去噪及增强

在图像信噪比低的情况下，图像分割算法效果一般较差，故去噪和增强是凝胶图像预处理的第一环节。对凝胶图像的采集过程分析可知，其噪声主要为椒盐噪声混合高斯噪声，对比多种滤波方法处理效果后，选择均值滤波。

对大量凝胶图像绘制其灰度直方图（图7）后发现，凹液面及毛细管内壁灰度级较低，直方图多呈现单峰型和多波谷的双峰型。

图7 灰度化图像及灰度直方图Fig．7 Grayscale image and its grayscale histogram

若使得灰度直方图均匀地分布在整个灰度区域内，则可将背景与毛细管区域明显区分开。目前常见的图像增强方法主要有线性变换、非线性变换和直方图均衡化，其中非线性变换sin函数变换曲线的特点是上、下波型变换平缓，中间变换尺度大。针对凝胶图像灰度值集中在某一范围内这一特征，用该算法进行拉伸区分背景与ROI区域十分有效。sin函数形式为：

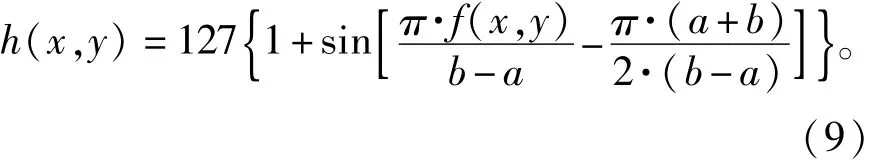
其中，a、b分别为图像输入时最低灰度值、最高灰度值，f（x，y）、h（x，y）分别为原图像和增强后的图像。经sin函数增强后的图像及灰度直方图如图8所示。

图8 sin函数增强后的图像和灰度直方图Fig．8 Sin enhanced image and its gray histogram

3．2 阈值分割

阈值分割是一种简单且有效的图像分割方法，其目的是通过选取合适的阈值将图像分割成若干个具有独特特征的区域或只提取感兴趣区域，为后续处理提供简单直接的依据。本文为得到黏度求解参数Δl，需要对凝胶图像凹液面进行准确提取，故对凝胶图像进行分割。为充分发挥最大类间方差（OTSU）阈值分割法准确性高和鲁棒性强的优点，首先采用Sobel边缘检测算子对凝胶图像进行处理后再利用OTSU法进行分割。

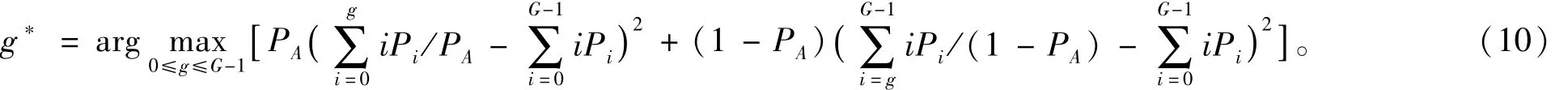
设图像灰度级为 G［1，2，3，…，G］，ni为灰度级为i的像素数。设以灰度值g将图像分为2个区域，即灰度级为［1，2，…，g］的背景区域 A，灰度级为［g＋1，g＋2，…，G］的目标区域B。记各灰度级出现的概率为Pi，像素出现在A区域的概率为PA，则出现在B区域概率为1-PA，从而可由OTSU准则［11］得到最佳分割阈值g*，分割处理结果如图9所示。

图9 毛细管凝胶图像分割结果示意图Fig．9 Schematic diagram of capillary gel image segmentation result

由图9（d）可以看出，管壁与凹液面的绝大部分被清晰地分割出来，但是因图像质量、光照等原因导致曲线分割并不完整。当出现凹液面分割完整度未及2／3情况时（如图10所示），在自适应分割测量方法［10］中此类图像将被作为残次图像剔除，但若一组连续运动的凝胶图像中残次图较多且均被剔除掉将使得样本数量骤减，导致凝胶黏度测量误差增大，测量精度降低。为保证样本图像数据量足够多，以提高系统测量稳定性及精度，本文测量方法在图像分割后对凹液面曲线进行完整性拟合。

图10 凝胶图像分割残次图Fig．10 Imperfect gel image segmentation result

3．3 表面张力曲线拟合

毛细管中凝胶溶液受到空气阻力作用，表面分子因受力不平衡而向内产生不同程度的收缩，宏观表现为一条曲线，本文将其定义为凝胶表面张力曲线。由图10可知，在用分割算法对凝胶图像处理时，并不能保证每一次分割都可得到有效的表面张力曲线，为提高本文测量方法的鲁棒性，在阈值分割后继续对表面张力曲线进行最小二乘椭圆拟合。

对表面张力曲线建立椭圆数学模型，设任意位置的椭圆方程为：

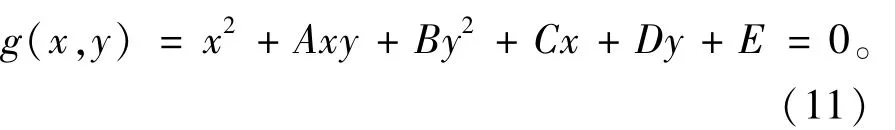
其中，A、B、C、D和E为任意椭圆方程的系数。

设点Qi（xi，yi）（i＝1，2，…，n）为表面张力曲线上n（n≥5）个测量点，由最小二乘法原理知，需使得目标函数

值最小，求解各参数，求解过程如下：

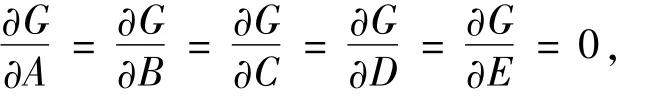
可由上式求解椭圆参数A、B、C、D和E，确定任意平面内椭圆的5个参数：椭圆中心（x0，y0）、长轴半径a、短轴半径b、偏角θ，即：

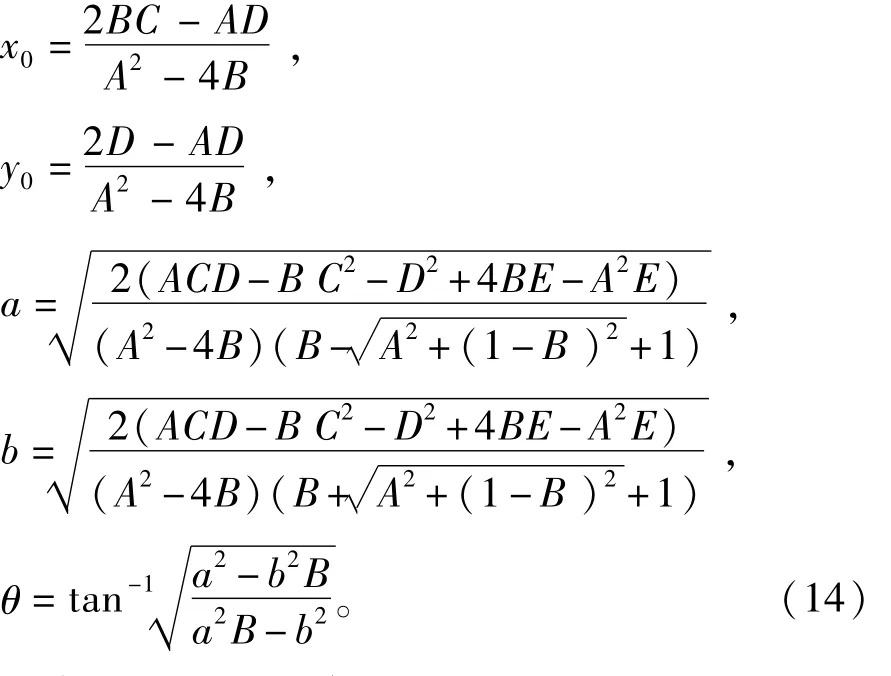
当求得上述5个参数后，即可实现对表面张力曲线精确拟合。对残次图像图10进行曲线拟合后结果如图11所示。

图11 图像拟合结果Fig．11 Image fitting result

3．4 曲率中心定位法

由前文测量原理知，求取黏度的核心是对Δl的精确测量。本文提出曲率中心定位法，即取表面张力曲线与毛细管中心线N的交点M（ji，ki），再在曲线上任取一点M′，求曲线g（x，y）上点M处曲率k：

其中：Δθ为点M与点M′处切线的转角；Δs为点M与点M′的弧长。

进而可求：

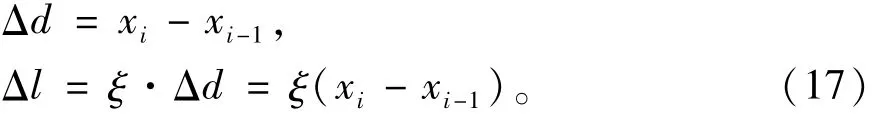
选取4组不同凝胶样品进行实验，对一次完整的凝胶运动过程人工求取前后相邻两张图像的表面张力曲线上最远点作为测量点的差值Δdp（像素差）。再采用曲率中心定位法求取相邻两张图像的差值Δdc（像素差），作两者的位移离散图。为验证本文测量算法的可靠性，选择在不同的压力环境下进行实验，位移离散图如图12所示。

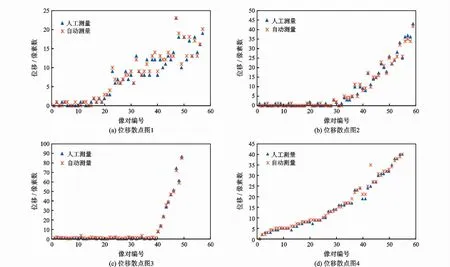
图12 位移散点对比图Fig．12 Comparison of displacement scatter points

实验结果显示，自动测量与人工测量结果总是基本保持一致，说明曲率中心定位法具有较高的鲁棒性。分析上图可知，在整个测量过程中为尽可能多地得到有效数据，应尽量在达到突破压力后对运动过程开始进行采集，以减少采集到因未达到突破压力而位移为0的像对，尽可能多采集产生位移的像对，使得像对位移散点图如图12（d）所示。

4 实验结果与分析

4．1 实验结果

为验证本文测量方法的可行性，选取西北地区某石油公司提供的4个批次已标定黏度值的凝胶溶液样品进行实验。工业相机采集的毛细管中凝胶溶液部分运动过程原图像及处理后图像如图13所示。

图13 凝胶部分运动过程原图像及处理后效果图Fig．13 Apart of original and processed images of gel in movement process

将3．4节中的Δdp和Δdc依据式（8）换算得Δlp与Δlc，分别带入式（6），计算出4组凝胶样品对应的黏度值，并随机选择其中10组像对计算结果进行对比，如图14所示。

图14中4组实验结果表明，计算机与人工测量结果基本保持一致，故本文设计的分析系统可以对凝胶物理特性黏度值进行测量，且具有较高的准确性和较强的鲁棒性，满足实际工程应用要求。另外，相对误差求解公式为：

图14 测量结果对比图Fig．14 Com parison ofmeasurement results

式中：δr为实际相对误差，δ为绝对误差，N为真值。由该公式计算本文测量方法所求黏度值的实际相对误差，见表2。

表2 实验测量结果Tab．2 Experimentalmeasurement results

从表2可以看出，本文凝胶测量系统测量结果与实际标定值相近，相对误差的绝对值最低为1．06%，测量精度高，且均未出现巨大误差，鲁棒性较强。

4．2 对比验证

为验证本系统具有较高的精度及可靠性，设计了对比验证实验。利用传统的毛细管黏度计、旋转式黏度计及自适应分割测量方法分别对相同的4种凝胶溶液进行测量，并计算每种方法测量结果的相对误差、误差率ψ及标准偏差σs。其中标准偏差越小说明数据稳定性越好，记测量次数为N时有：

其中：ηi为每一次测量的黏度样本值，ηav为测量系统对同一凝胶样品测量N次后所求的黏度平均值。

具体测量结果对比见表3。

表3 测量结果对比Tab．3 Comparison ofmeasurement results

从表3可以看出，本文测量系统的平均相对误差、误差率和标准偏差均优于其他3种方法，其中平均相对误差、误差率分别为1．58%和1．26%，表明本文方法测量精度较高。此外，标准偏差仅为0．012，证明本文测量系统具有较强的稳定性和较高的可靠性。

5 结 论

本文利用工业相机、毛细管、显微镜、驱替泵等装置构建了测量凝胶黏度的简易系统，并通过图像处理技术实现了凝胶黏度的非接触、高精度测量。与市面上的凝胶黏度测量仪器相比，本文所设计的测量系统具有易于操作、便携、成本低等特点。此外分别对4种不同黏度的凝胶样品进行分析，测量的黏度平均相对误差为1．58%，实验结果表明本文系统精度高，鲁棒性较强，更适用于工程领域中应用。