基于蚁群算法优化的RBF-BP神经网络在光伏阵列MPPT的应用＊

无锡科技职业学院 周谢益

针对光伏电池输出非线性的特点，为高效地追踪光伏电池的发电输出功率，本文提出了一种基于蚁群算法优化的RBF-BP 组合神经网络，用于对光伏阵列最大功率点追踪（MPPT）。本文依据光伏电池的输出特性，首先提出构建RBF-BP 双隐层组合神经网络，在此基础上运用蚁群算法对组合神经网络进行优化。将影响光伏电池输出特性的主要因素光照强度和外界环境温度作为神经网络输入端建立预测模型，通过Matlab 对该模型进行仿真。仿真结果表明，优化后组合神经网络相较于传递神经网络具备追踪精度高、速率快、迭代次数少等优点。

随着新能源技术的不断发展，太阳能作为一种环保可再生能源目前已经广泛应用于多个新能源领域。光伏发电技术作为能将太阳能直接转化成电能的可再生能源技术[1]，已经得到了越来越广泛的关注。由于光伏电池的发电输出具有明显的非线性，其发电效率特别是光伏发电最大功率受光照强度和外界环境温度影响较大。为提高光伏发电效率，对光伏发电最大功率点追踪就显得尤为必要。近年来，国内外学者提出了多种最大功率点的追踪算法，主要有扰动观察法[2]、电导增量法[3]和神经网络法[4，5]等。扰动观察法的优势是在光照变化速率较快时具有较好的效果，缺点是对传感器精度要求高，算法计算效率较低。电量增量法的劣势在于步长固定，步长设置过小时光伏阵列的预测结果易滞留在低功率输出区，步长设置过大时，光伏阵列的预测结果大幅振荡。人工神经网络具有较强的非线性函数逼近能力，并且在建立模型时不依赖光伏电池的物理特性。主流人工神经网络主要有BP[4]和RBF[5]神经网络两种。BP 神经网络的优势是自学能力较强，但训练网络过程中容易受偏差样本误导；RBF 神经网络的优点是收敛速度快，但是其泛化能力差。本文提出建立一个同时具备两者优点的RBF-BP 双隐层组合神经网络，通过蚁群算法[6]进一步优化该神经网络。由Matlab 进行仿真与分析，经检验蚁群算法优化后组合神经网络，具备训练时长短，预测精度高的特性。

1 光伏电池的输出特性

光伏电池是利用太阳能的光生伏特效应[7]，将光能转换成电能的一种装置，其输出特性受光照强度和外界环境温度等因素的综合影响，具有明显的非线性特点。当外界环境温度恒定时，光照强度越大，光伏发电板输出功率越大，最大功率的值也越大，其对应的最大功率点处的电压也越大；当光照强度恒定时，外界环境温度越高，光伏发电板输出功率越小，最大功率点的值也越小，其对应的最大功率点处的电压也越小。

由于光伏电池的输出功率是一个动态变化的非线性过程，为提高光伏电池发电效率，提高光伏电池最大功率点追踪的精度和速度尤为重要。

2 基于蚁群算法优化的RBF-BP 神经网络的MPPT策略研究

2.1 RBF-BP 神经网络

常见的人工神经网络主要有BP 和RBF 神经网络两种。本文提出构建一种结合BP 神经网络和RBF 神经网络的组合神经网络，具备学习能力强、自适应度高收敛快等优点。该组合神经网络由输入层、双隐含层和输出层组成，其中双隐含层由RBF 子网与BP 子网构成。样本数据经由输入层首先映射到第一层RBF 隐含层，其训练结果作为第二层BP 隐含层的输入层，最终预测结果由输出层得出。

2.2 蚁群算法优化RBF-BP 神经网络

RBF-BP 组合神经网络搭建初始权值和阈值为[0，1]之间的随机数，输入样本训练后为满足精确度要求，RBFBP 神经网络依据学习结果的实际情况反向修改权值和阈值。由于初始权值和阈值随机性较大，一定程度上影响神经网络的训练效率。为了解决初始权值和阈值不确定性对RBF-BP 组合神经网络训练效率影响，本文提出运用蚁群算法对RBF-BP 组合神经网络进行进一步优化。

蚁群算法优化RBF-BP 组合神经网络具体步骤如下：

（1）根据光伏发电输出特性，本文选取光伏电池板所在环境温度和对应光照强度及在此条件下的光伏电池板发电输出功率作为RBF-BP 组合神经网络训练的输入项和输出项。另选取同等条件下各个时段的部分样本数据作为RBF-BP 神经网络训练完成后的测试样本。

（2）建立RBF-BP 神经网络用于训练归一化后的样本数据。

（3）网络初始化后确定蚁群算法最大最小信息素、各集合中随机数个数、隐层数、每个隐层最大节点数、蚂蚁数目及最大循环次数等。

假定选择值集合为C={0，1}，其中0 表示蚂蚁没有选择此节点，1 表示蚂蚁选择了该节点，它们的初始信息素都为τ0，在MMAS 算法中τ0 取τmax。节点nij的阈值对应有一个集合，即Ib；权值共有p个集合，p的取值等于第i-1 层的节点个数Si-1(当i=1 时，p的取值等于输入层节点数SI)，且每个权值集合都与i-1 层的节点一一对应。

（4）所有蚂蚁从第一个节点开始，采用并行方式，即当所有蚂蚁完成对某一节点的处理后，才继续下一节点，直到完成对所有节点的处理。

元素选择规则：对任意一个节点，考虑其阈值集合Ib，蚂蚁k选取第j个元素的概率如式（1）所示：

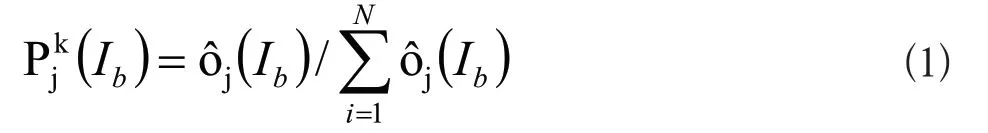
τi(Ib)表示集合Ib 中第i 个元素的信息素。节点及权值元素的选择均与上述规则一致。

（5）在本次迭代中，按m 只蚂蚁构建的解依次建立对应的神经网络，输入训练数据并计算网络的MSE。记录蚂蚁所找到的最优解MSEbest'，用RBF-BP 算法训练该神经网络一次，记录训练之后的MSEtrain、权值和阈值。

（6）重复步骤（4）、步骤（5），直到最大循环次数，退出循环。

（7）利用蚁群算法优化后RBF-BP 神经网络权值阈值后，训练网络。

3 仿真预测结果及分析

本文实验选取Matlab R2010 作为仿真平台，实现上述提出的基于蚁群算法优化后的RBF-BP 组合神经网络并取于样本数据进行测试。实验数据来自文献[8]中提供的一天之中光伏发电板从早6 点至晚6 点g 共12 个小时间隔5 分钟的光伏发电板环境温度和光照强度144组数据，测试数据为次日早6 点至晚6 点随机时间间隔光伏发电板环境温度和光照强度24 组。通过Matlab 对蚁群算法优化的RBF-BP 组合神经网络进行编程设置，RBF-BP 组合神经网络训练函数采用Trainlm，RBF 隐含和BP 隐含层分别采用Radbas 函数和Tansig 函数作为传递函数，输出层的传递函数采用Purelin 函数。网络的最大训练次数设置为1000 次，训练的期望误差设置为0.00001，学习速率设置为0.001。作为对比参照，在相同训练数据下，通过Matlab 直接训练RBF-BP 组合神经网络训练。训练迭代次数对比如图1所示。

图1(a)和图1(b)分别为RBF-BP 组合神经网络训练迭代曲线图和蚁群算法优化后RBF-BP 组合神经网络训练误差曲线图。在训练数据和样本数据有限的情况以及同等误差精度要求下，RBF-BP 组合神经网络需要训练迭代43 步，蚁群算法优化后的RBF-BP 组合神经网络只需要训练39 步，训练效率提升显著。

精度方面，由图1(a)和图1(b)Matlab 中的MSE 函数得出蚁群算法优化后RBF-BP 组合神经网络均方误差为9.23791×10-5，相较于RBF-BP 组合神经网络均方误差分别为1.3573×10-4，实现了在训练时间更短（迭代次数少）的情况下，神经网络预测精度更好。

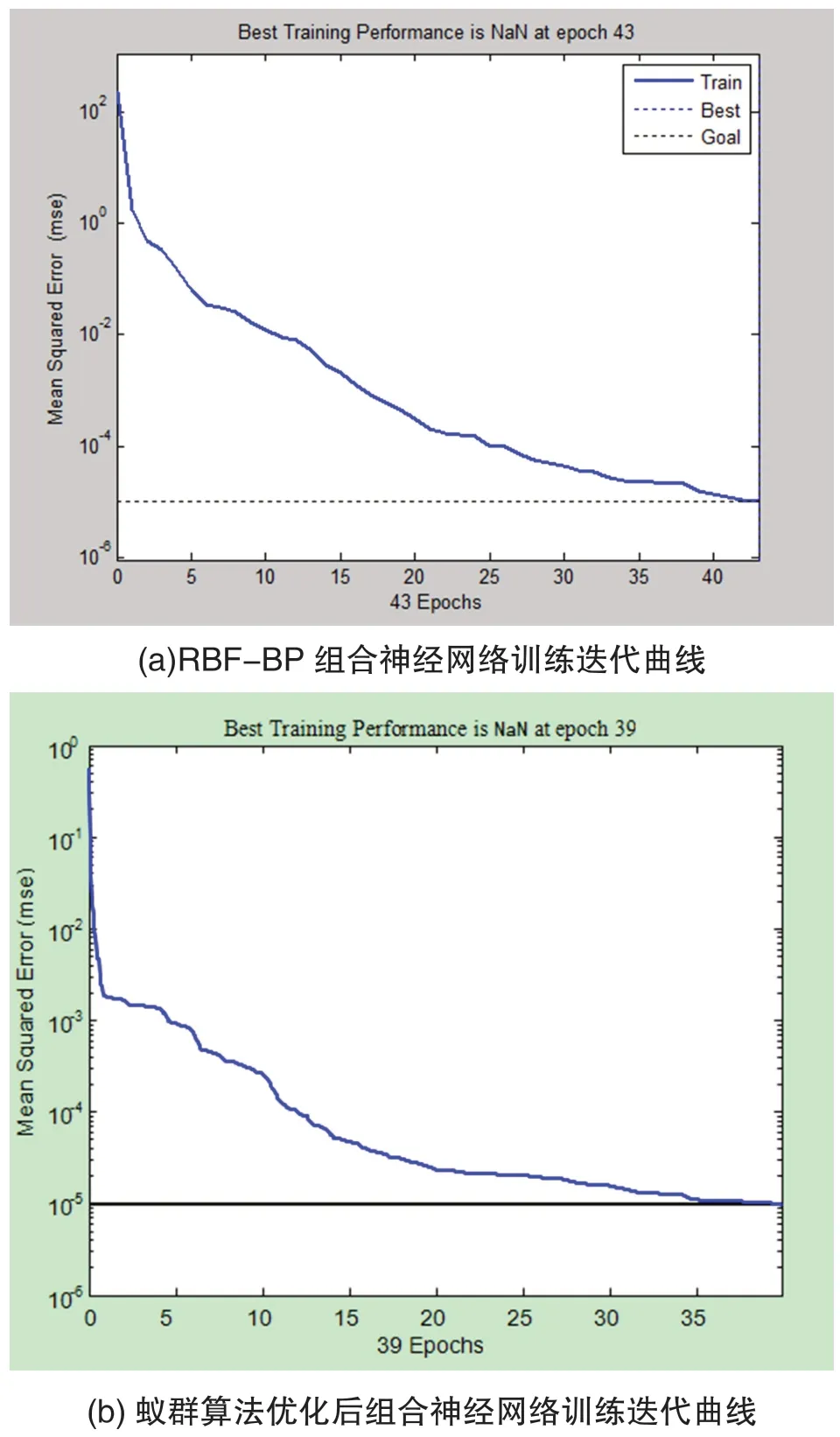
图1 神经网络训练迭代次数对比图Fig.1 Neural network training iterations comparison graph

为验证蚁群算法优化后的RBF-BP 组合神经网络的精确度，如图2所示给出24 组测试随机采样点实际预测输出功率与实测功率的分布图。由图2分布图可以看出误差值在0.03 ～-0.02 之间，说明利用蚁群算法优化的RBF-BP 组合神经网络对光伏电池最大功率点地追踪具有较高的准确性。

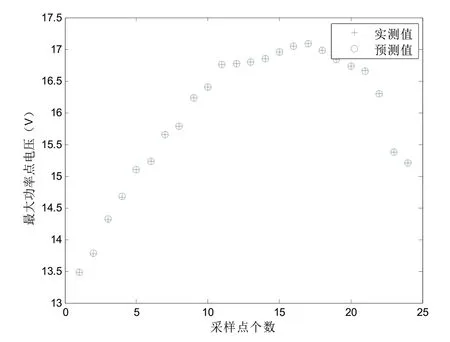
图2 训练后神经网络预测功率与实际功率分布图Fig.2 Prediction power versus actual power distribution

4 结语

本文提出一种基于蚁群算法优化的RBF-BP 组合神经网络，通过蚁群算法优化RBF-BP 组合神经网络权值和阈值，是RBF-BP 组合神经网络具备更快的收敛速度，在更少迭代次数的情况下实现更高的精准度。仿真实验结果表明蚁群算法优化后组合神经网络无论是从迭代次数和预测精确度上均优于单独RBF-BP 组合神经网络。验证了蚁群算法优化RBF-BP 组合神经网络的可行性，有效提高了光伏阵列最大功率点追踪的问题。