决策树算法在高校毕业生就业预测中的应用——以普洱学院为例＊

普洱学院 王娇

近几年，我国大学毕业生数量不断增多，毕业生的就业问题是当前高校工作的重点。运用行之有效的方法分析预测就业趋势具有实际意义。该文将数据挖掘技术用于应用型高校毕业生就业情况的分析中，利用普洱学院毕业生就业数据，引入C4.5 算法，计算信息增益率指标，构建分类决策树，建立毕业生就业预测模型。通过对模型的测试，构建模型预测结果混淆矩阵，得到预测模型的准确率达到83.33%。

就业是民生之本，对经济发展有着重要的作用[1]。近些年，高校招生规模不断扩大，随之大学毕业生群体也在不断地壮大。2022年高校毕业生总规模达到1076 万人，创下历史新高，且受到新冠疫情的影响，毕业生就业压力随之增大，且需要面临更加复杂严峻的形式。为适应社会发展，国家相关部门支持各大高校转型为应用型大学，鼓励培养应用型人才。国家对应用型高校毕业生就业工作十分地重视。

在信息收集和分析手段有限的年代，不仅无法全面了解毕业生的在校信息，而且也无法精准、及时的掌握毕业生就业情况。随着现代社会信息化程度越来越高，大数据技术应用到了各行各业中。在许多方面，数据挖掘技术被广泛地运用在教育教学中，如：关联分析技术、决策树算法、随机森林算法、神经网络等技术。利用数据挖掘技术发现数据中蕴藏的有价值信息，指导实际工作。

教育及就业相关的数据库中的数据量迅速增长，各省大学生就业信息管理系统逐渐建立完善，对大学生在校学习情况及毕业就业情况能够较全面的掌握。但是，目前对于现有的信息管理系统，管理者主要还是侧重于查询、更新、存档等功能，并未充分利用管理系统中的数据进行深入分析[2]。如何挖掘应用型高校毕业生就业数据的价值，而数据挖掘技术恰恰就是最好的解决方法[3]。在数据挖掘中，分类是一项非常关键的分析手段，实现分类的方法有多种，如：异常检测、决策树、随机森林等。

利用现有就业数据进行合理预测，将为应用型高校在制定学生培养计划和能力提升方面提供理论依据。本文基于决策树C4.5 算法，对普洱学院毕业生的就业数据进行分类研究，通过设置英语成绩、计算机成绩、专业课成绩、是否挂科、是否就业等变量，建立关于就业的C4.5 决策树模型。

1 相关概念

1.1 决策树

决策树是数据挖掘分类算法中常见分类方法，通过有效的监督学习，输出容易理解的结果，可用于分类及预测。1966年，Hunt 等人在其研发的概念学习系统中首次提出决策树的概念[4]。自1986年Quinlan J R 提出了ID3 算法后，该算法在机器学习等多领域都得到了很大的发展，因此在数据挖掘和应用中具有较好的前景。决策树在各个领域中运用非常广泛，如医学疾病分类、气象分类、银行用户分类、电子邮件分类等。利用训练集数据集构建分类决策树后，可以利用测试集数据集对模型的分类进度进行检验，以此确定所构建的模型是否适用于分析该问题。决策树是一种通过从上到下的递归形式，以树状形式呈现分类规则和分类结果的算法，在树的每一个节点上通过对比并选择属性值，以此判断该节点向下的分支，在树的叶节点处得到分类结果[5]。决策树分类结果易于使用者理解，算法实现容易，它不需要使用者具备更多的数据挖掘知识，便可通过决策树诚信的树形结果进行分析、理解。实现决策树常见的算法包括：ID3、C4.5、CART 和CLS 等[6]。

1.2 ID3 算法

ID3 算法是由J.Ross Quinlan 提出。该算法把信息论中的一些概念引入其中，以信息熵和信息增益作为基础，以此作为数据属性划分的标准，最终实现对数据集的分类。

1.2.1 信息熵

Shannon 在1948年把热力学中的熵引入信息论，提出了信息熵的概念，又被称为香农熵。他用数学公式的形式阐明了概率与信息冗余的关系。利用熵可以把随机变量的不确定程度描述出来。

设X为离散型随机变量，概率分布为：

p(xi)=P(X=xi),i=1,2,3,…,n

Shannon 把随机变量X的熵H定义为：

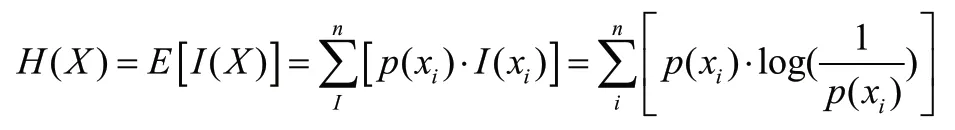
随机变量X的熵依赖于X的分布，约定0 ·log0 = 0。

1.2.2 条件熵

条件熵H(Y|X)是在X已知的条件下Y的不确定性，定义为：

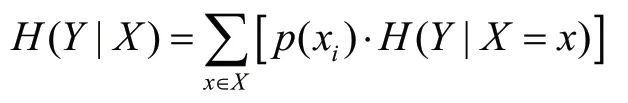
1.2.3 信息增益

信息增益是在X已知的条件下，Y的熵值较没有任何条件确定时减少的程度[7]。定义为：

Gain(Y,X)=H(Y)-H(Y|X)

信息熵与条件熵相减就是信息增益。一般，信息增益越大，表示所用划分属性获得的“纯度增加”越大。ID3 算法以此选择决策树的划分属性，一般用于处理离散型数据。从信息增益计算公式中可以看出，该算法具有倾向于取值较多的特征[8]。

1.3 C4.5 算法

J.Ross Quinlan 对ID3 算法进行改进提出了C4.5 算法，信息增益率作为该算法划分属性的判断指标[9]。ID3算法的所有优点都能在C4.5 算法中体现出来。同时，C4.5 算法可以处理离散变和连续变量，消除了ID3 算法的多值特征倾向[10]。与ID3 算法相比，C4.5 算法在效率和准确程度上也有很大的提高[11]。

信息增益率在信息增益的基础上兼顾了为获取信息增益所付出的“代价”，消除了特征取值较多时带来的影响，等于信息增益除以特征的固有值，定义为：

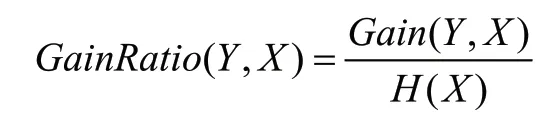
确定各属性的信息增益率，选取信息增益率最高的属性作为根节点，以此标准进行迭代，最终构建出分类决策树。

本文利用C4.5 算法对毕业生的就业相关数据进行分类分析。主要探讨该算法在应用型高校毕业生就业预测中的可行性。通过建立就业预测模型，希望为高校开展就业指导工作提供帮助。

2 基于决策树算法在应用型高校毕业生就业预测中的应用

2.1 数据来源及梳理

本文选取毕业生中英语成绩、计算机成绩、专业课成绩、是否挂科、是否就业5 个变量，随机抽取普洱学院数学与统计学院12 名毕业生的相关数据建立决策树模型。为方便建模，对采集到的数据进行预处理。从教务系统中导出学生各科在校成绩，对各类型科目取平均成绩，如：英语成绩为大学外语1 和大学外语2 的平均值。且认定85 分以上为优秀，70 ～85 为良，70 分以下为差，数据如表1所示。

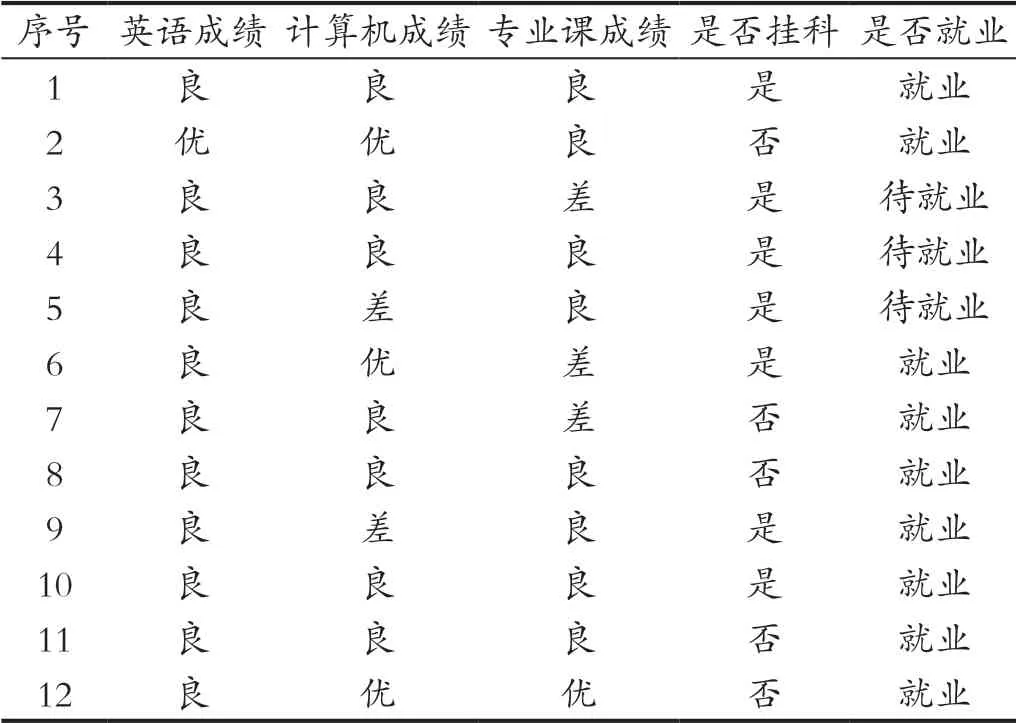
表1 毕业生情况表Tab.1 Graduate fact sheet

2.2 模型构建

2.2.1 计算类别的信息熵

在样本数据中，9 人就业，3 人未就业，故P就业=9/12，P未就业=3/12。由信息熵计算公式可得：

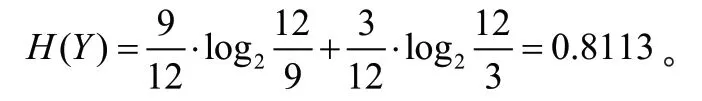
2.2.2 分别计算每一个属性划分方式的条件熵

以英语成绩为例，令随机变量X 为英语成绩，则X取值为{优、良}，其概率分别为根据条件熵计算公式可得：

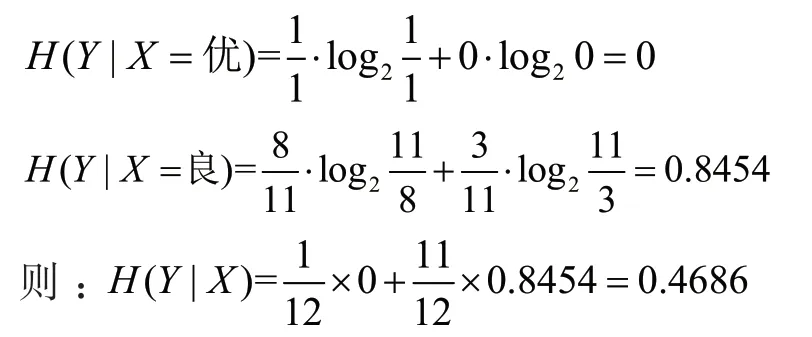
同理可计算出属性“计算机成绩”“专业课成绩”“是否挂科”的条件熵分别为：0.6701、0.7704、0.2704。

2.2.3 计算信息增益

根据信息增益计算公式可得：

Gain(Y,X) =0.8113-0.4686=0.3427

同理可计算出属性“计算机成绩”“专业课成绩”“是否挂科”的信息增益分别为：0.1412、0.0409、0.5409。

2.2.4 计算属信息增益率

根据信息增益率计算公式可得：

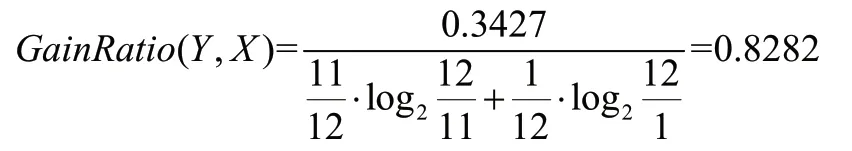
同理可计算出属性“计算机成绩”“专业课成绩”“是否挂科”的信息增益率分别为：0.1020、0.0344、0.5890。

2.2.5 建立决策树模型

由计算结果可知，属性“英语成绩”的信息增益率最高，故选择该属性为分裂属性作为根节点。分裂后，“英语成绩”为优的条件下，类别是“纯”的，即毕业生就业情况类别均为就业，故把此定义为叶节点。从“英语成绩”为良向下继续进行分裂，依次按照2.2.1 ～2.2.4 的方法进行计算，构建出C4.5 算法的决策树，如图1所示。

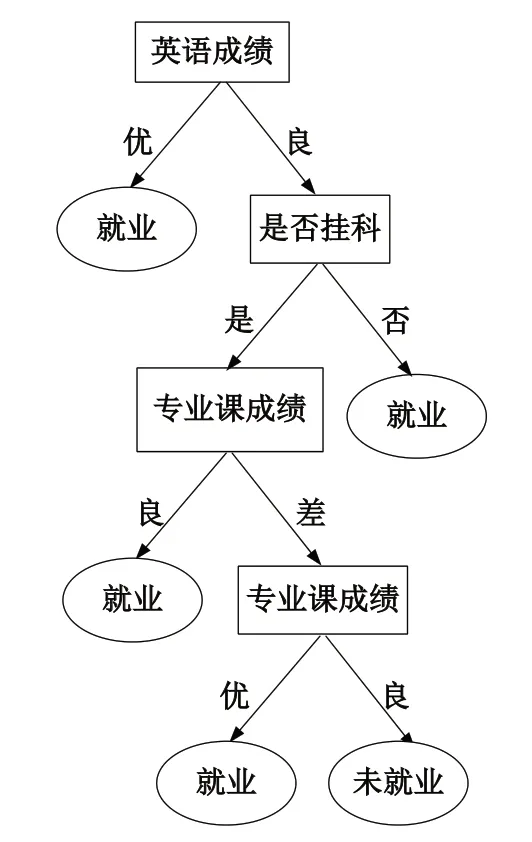
图1 毕业生就业预测模型图Fig.1 Graduate employment prediction model diagram

2.2.6 模型预测

为验证决策树模型的精确度，根据图1的决策树，对样本数据精选了验证，利用验证结果得到预测混淆矩阵，如表2所示。结果表明，该决策树模型精确度达到83.33%，模型能够得到较好的预测结果。

表2 预测结果表Tab.2 Forecast result table

3 结语

本文采用决策树C4.5 算法，对普洱学院毕业生的就业数据进行了分析，得到了预测精度较高的决策树分类模型。预测模型能够处理定性数据和定量数据，能够很好地适应就业相关数据的分析，模型构建简单、快速，结果直观，便于理解。能够为应用型高校毕业生就业情况的预测提供有效的预测，为高校帮扶毕业生就业提供一定的理论基础。本文不足之处在于，训练样本较少，可能存在一定的偏差，在进一步地研究中将选取更大的训练样本，考虑更多的相关属性。