基于PLC技术的高精度数控机床加工轨迹控制方法

常州刘国钧高等职业技术学校 胡丞熙

针对传统方法在高精度数控机床加工轨迹控制实际应用中存在误差较大的问题，提出基于PLC 技术的高精度数控机床加工轨迹控制方法。通过对数控机床运动学正变换和逆变换，求解数控机床刀具驱动位移，建立数控机床运动数学模型，通过将读取到的刀具实际点位数据与理想轨迹比对，预测出高精度数控机床加工轨迹误差，利用PLC 技术对误差点位坐标转换，以及中心指令点拟合，生成加工轨迹控制程序，通过数控机床运动数学模型输出，实现对数控机床加工轨迹优化控制。经实验证明，应用设计方法机床加工误差小于传统方法，在机床加工轨迹控制方面具有良好的应用前景。

数控机床作为一种零件加工设备，已经被广泛应用到多个领域中。随着加工行业对精度要求的不断提高，在传统数控机床的基础上，通过优化刀具、伺服给进系统等，逐渐衍生出高精度数控机床，目前高精度数控机床已经被广泛应用到航空航天制造业、汽车制造业等行业[1]。评价高精度数控机床的加工精度是衡量机床工作性能的关键指标，受到机床自身因素或者外界因素影响，高精度数控机床在加工过程中可能会存在动态误差或者静态误差，误差的存在直接影响着高精度数控机床加工轨迹，从而机床加工生产的产品质量无法达标，因此对高精度数控机床加工轨迹控制是非常有必要的。针对高精度数控机床加工误差问题，国外研究者从不同的角度提出了多种解决办法，提出了高精度数控机床加工轨迹优化控制方法，以及加工轨迹插补方法。但是国内高精度数控机床加工轨迹控制技术起步比较晚，虽然近几年掀起了研究热潮，但是现有的控制方法在实际应用中控制效果仍旧比较差，由于控制流程比较复杂，计算量较大，控制后数控机床加工轨迹与理想加工轨迹仍然存在较大的误差，已经无法满足高精度加工需求，为此提出基于PLC 技术的高精度数控机床加工轨迹控制方法。

1 高精度数控机床加工轨迹控制

对于高精度数控机床加工轨迹的控制，涉及数控机床的运动学，故此次设计的控制方法，第一步为建立数据机床运动数学模型，对高精度数控机床运动学以数学形式描述，将其作为控制对象；第二步，通过读取数控机床加工文件中相关数据，获取到数控机床运动轨迹坐标信息，并预测分析出数控机床加工轨迹误差；第三步，根据预测结果，利用PLC 技术重新编码数控机床加工轨迹，通过刀具空间位置坐标系转换和中间指令点拟合，对原有的运动轨迹进行调整和优化，实现对高精度数控机床加工轨迹的控制。

1.1 建立数控机床运动数学模型

数控机床运动数学模型是加工轨迹控制转换工具，由于其运动符合线性规律，可以利用数学方程式的形式将其运动轨迹表示出来[2]。数控机床运动轨迹为机床刀具位置在三维空间内的变换所形成的路径，其位置的变换主要依靠变换矩阵，假设数控机床工作面空间坐标系为N，在该三维坐标系中刀具绕空间坐标轴做旋转、平移运动，故数控机床运动坐标变换为：

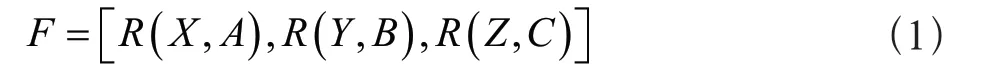
公式（1）中，F表示数控机床运动坐标变换数学模型；R(X，A)、R(Y，B)、R(Z，C)分别为数控机床刀具绕空间坐标系X、Y、Z坐标轴、沿矢量平移A、B、C的变换矩阵[3]。为了进一步对数控机床加工运动学数学描述，基于数控机床运动坐标变换数学模型，对数控机运动学逆变换和正变换。

逆变换是将刀具向空间坐标轴位移脉冲当量的转换，假设数控机床工作面空间N中刀具参考点的位置信息为n，其中包括刀具参考点位的坐标、角度等信息，当机床刀具的摆动角度为零时，此时高精度数控机床可以等效为一个三轴联动机床，刀具的驱动位移可表示为：

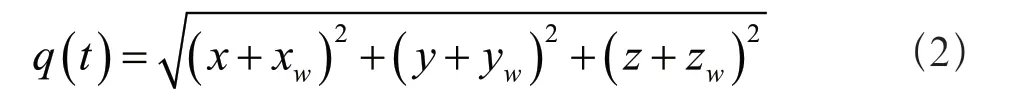
公式（2）中，q(t)表示刀具摆动角度为零情况下，在t时刻驱动刀具的位移；x、y、z表示在空间坐标系中刀具参考点位横坐标、纵坐标、斜坐标；xw、yw、zw表示刀具偏置矢量的横坐标、纵坐标和斜坐标[4]。当刀具的摆动角度不为零时，此时高精度数控机床可以等效为一个五轴联动机床，刀具的摆动角度由刀具绕坐标轴的角度所决定，利用欧拉角的形式描述刀具的位姿，进而可以求出刀具的驱动位移，其用公式表示为：

公式（3）中，q0(t)表示刀具摆动角度不为零情况下，在t时刻驱动刀具的位移；r表示刀具参考点在固定参考坐标系中的方位矢量；a表示三维空间坐标系N相对于固定参考坐标系的欧拉角；b表示刀具的姿态矢量；x0、y0表示参考点在固定参考坐标系中的横坐标与纵坐标。

正变换是将刀具向空间坐标轴位置与摆动角度的变换，假设数控机床各支链转动副的转角为α，根据牛顿-拉斐逊数值理论，可以将数控机床运动学正变换表示为：

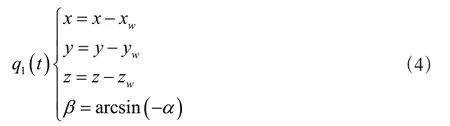
公式（4）中，q1(t)表示数控机床运动学正变换位移；β表示数控机床刀具摆动角度[5]。通过以上数控机床运动学正变换和逆变换分析，建立数控机床运动数学模型为：

公式（5）中，Q表示数控机床运动数学模型，在该数学模型上控制机床加工轨迹。

1.2 加工轨迹误差预测

高精度数控机床所有运动数据都记录在机床的加工文件中，利用OSHFI 读卡器对数控机床加工文件中所有刀具点位数据读取，将其作为加工轨迹误差预测的数据依据。数控机床运动轨迹可以分解成为直线和曲线两种，其轨迹误差为直线轨迹误差与曲线轨迹误差总和，因此需要对这两种误差进行计算。将获取的点位数据与理想点位比对，可以得出高精度数控机床的直线轨迹误差，机床直线轨迹误差如图1所示。

图1 高精度数控机床直线轨迹误差示意图Fig.1 Schematic diagram of linear trajectory error of high precision cnc machine tool

如图1可以看出，γ表示数控机床理想轨迹与空间坐标系中的横坐标轴的夹角，点T为数控机床刀具运动指令位置点，G为当前数控机床刀具实际位置点，m为数控机床刀具实际位置点与理想轨迹最近距离直线的交点，根据这几个点的几何关系，求出数控机床直线运动横坐标轴跟随误差和纵坐标轴跟随误差，进而求出数控机床直线轨迹误差：

公式（6）中，c表示数控机床直线运动轨迹误差；s表示横坐标轴的跟随误差；l表示纵坐标轴的跟随误差[6]。假设数控机床参考圆弧曲线轨迹为ρ，该曲线圆弧的圆心为ε，根据数控机床刀具参考点与实际点位的几何关系，求出数控机床曲线误差：

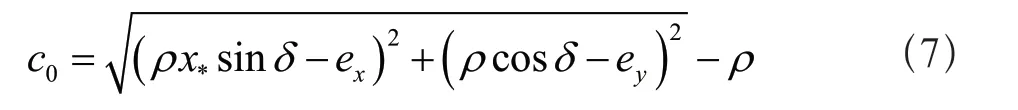
公式（7）中，c0表示数控机床曲线运动轨迹误差；x*表示圆弧曲线圆心ε的横坐标；δ表示圆弧曲线上过期望加工点的切线与横轴的夹角；ex表示实际加工点的横坐标；ey表示实际加工点的纵坐标[7]。将以上计算得出的直线运动误差c与曲线运动误差c0相加，即可得到高精度数控机床加工轨迹误差，为后续加工轨迹实时插补控制提供依据。

1.3 基于PLC 技术的加工轨迹实时插补控制

在上述基础上，利用PLC 技术对加工轨迹实时插补控制，生成加工轨迹实时插补控制程序，并通过可编程逻辑控制器（PLC）执行，其控制程序如下。

打开待控制的高精度数控机床的刀位文件，根据刀位误差，将刀位工件坐标系转换为高精度数控机床坐标系，实现误差优化后的坐标转换，假设P为与工件固联的刀具坐标系，工件中心点为该坐标系的原点，L为数控机床刀具与定轴固联的坐标系，该坐标系原点在工件固联坐标系P的位置矢量为J，建立完坐标系后，利用以下公式确定工件坐标系下误差点位在数控机床空间坐标系下的对应值：

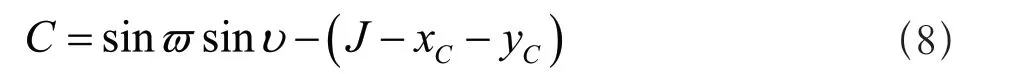
公式（8）中，C表示误差点位在数控机床空间坐标系下的对应值；ϖ表示工件坐标系下刀轴矢量对应的机床坐标系下的旋转角度；υ表示误差点位绕机床坐标系横坐标轴的旋转角度；xC、yC分别表示误差点位的横坐标和纵坐标[8]。

根据上述公式计算结果，在工件坐标系中对误差点位进行调整，使其恢复到理想点位上，其用公式表示为：

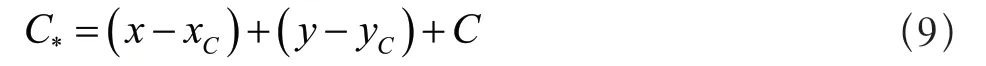
公式（9）中，C*表示转换后的工件坐标系中刀具坐标。通过PLC 技术对中间指令点拟合，使数控机床运动数学模型输出的运动点集形成新的刀具轨迹，使刀具运动点坐标无线接近转换后的刀具坐标，对其进行插补控制[9]。考虑到直接使用直线段对误差点位进行逼近，会破坏掉原曲线的连续性，致使在数控机床加工轨迹插补控制过程中，机床的速度和加速度不连续，因此采用曲线拟合方法对中间指令进行拟合，其拟合公式为：

公式（10）中，Zu表示中间指令拟合曲线；ϑ表示节点向量；Pi表示曲线参数；κ表示权值，为了简化运算，将该权值默认为1。通过中间指令曲线拟合，使数控机床运动数学模型输出的点位逼近理想轨迹，以此消除轨迹误差。将以上程序使用编码编写在可编辑逻辑控制器（PLC）中，将PLC 与高精度数控机床伺服电机连接，通过执行控制程序，调整高精度数控机床刀具加速度以及刀具移动姿态，从而实现基于PLC 的高精度数控机床加工轨迹控制。

2 实验论证分析

实验以某高精度数控机床为实验对象，该数控机床型号为SAFAE/55414，是典型的立式数控机床，刀具直径为80-300mm，刀具重量为8kg，该数控机床目前主要用于加工汽车零部件，对加工精度要求较高，利用此次设计方法与传统方法对该高精度数控机床加工轨迹进行控制。实验以8 种汽车零部件为高精度数控加工对象，开启数控机床开关，根据零部件加工需求，将数控机床的加速度设定为45000mm/s3，给进速度设定为100mm/s，每个零部件各加工1000 件，将准备好的OSHFI 读卡器与数控机床生产系统连接，并通过USB 接口接收到数控机床加工文件中的刀位数据，具体如表1所示。

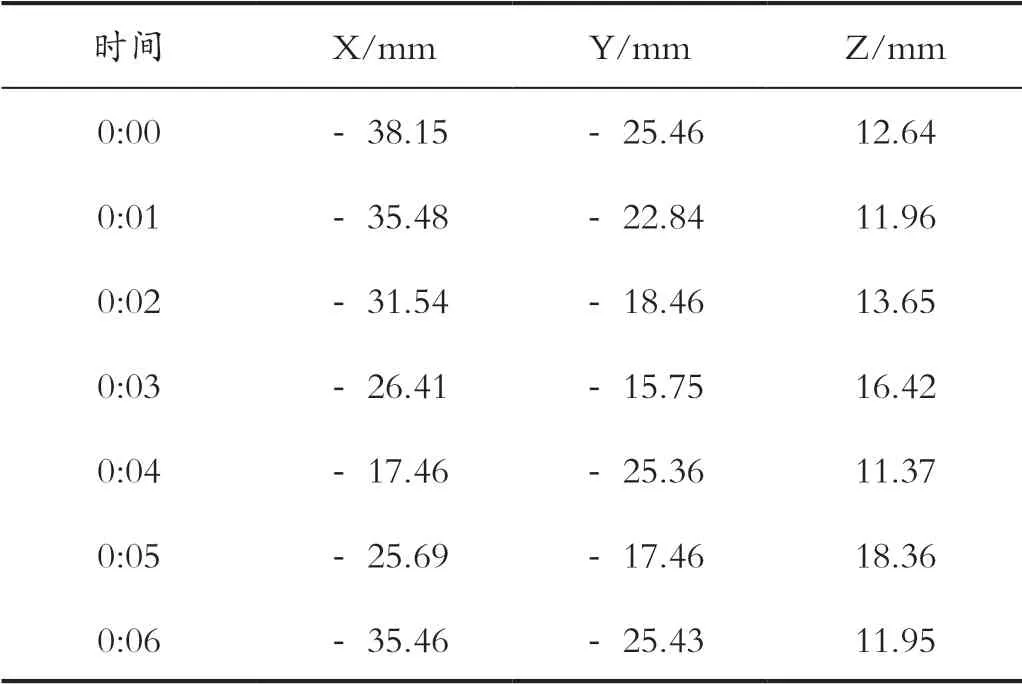
表1 数控机床刀位文件中刀位数据Tab.1 Tool position data in tool position file of nc machine tool

通过对读取到的刀位数据分析、误差预测、插补控制，完成零部件加工任务。实验使用专用测量仪器对每个加工部件加工误差进行测量，取平均值作为最终加工误差，并使用电子表格对数据进行记录，两种方法应用下机床加工误差对比如表2所示。

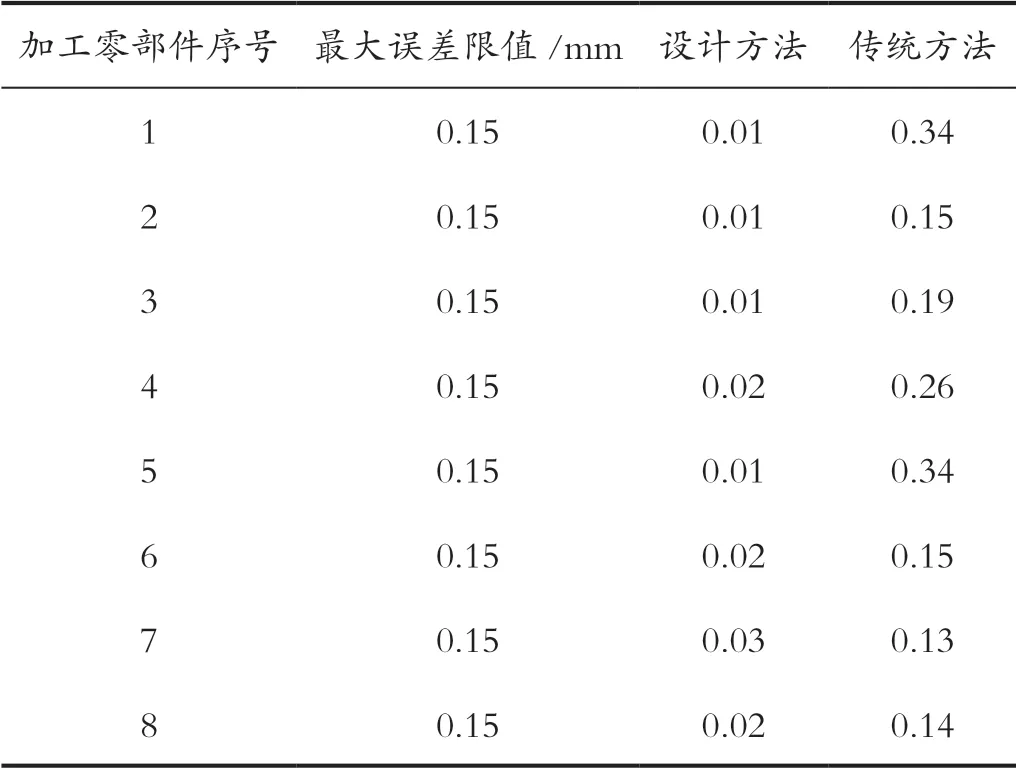
表2 两种方法应用下机床加工误差对比（mm）Tab.2 Comparison of machining errors of machine tools under the application of two methods (mm)

通过对表2中数据分析可以得出结论：应用设计方法对高精度数控机床加工轨迹控制后，零部件加工误差最大仅为0.03mm，最小加工误差为0.01mm，均在误差允许范围内，说明应用设计方法高精度数控机床运动轨迹与理想轨迹基本一致，设计方法具有良好的控制效果；而应用传统方法对高精度数控机床加工轨迹控制后，加工的零部件误差最大为0.34mm，远远超出误差允许范围，而且最小加工误差也已经达到了0.13mm，远远高于设计方法，因此实验结果证明了，在控制精度方面设计方法优于传统方法，能够有效控制高精度数控机床加工轨迹，相比较传统方法更适用于高精度数控机床加工轨迹控制。

3 结语

将PLC 技术与数控机床加工轨迹控制融合，提出了一个新的加工轨迹控制思路，并通过实验验证了该思路的可行性，此次研究有助于提高高精度数控机床加工精度，同时还有助于提高生产质量，以及高精度数控机床加工轨迹的控制技术水平，具有良好的现实研究意义。但是由于该方法尚未在实际中进行大量的操作和应用，在某些方面可能存在一些不足之处，今后会对基于PLC技术的高精度数控机床加工轨迹控制方法优化研究，为高精度数控机床加工轨迹的控制提供有力的理论支撑。